Sì, lo so... vi sto tartassando con varie configurazioni nello spaziotempo di Minkowski, quando intorno a noi tutto viaggia a velocità ben minore di quella della luce... Torniamo a Galileo, cercando di agire come facciamo con Minkowski. Viva la grafica!

Consideriamo un semplice problema di cinematica che può risolversi molto facilmente con una formula estremamente banale (quella della velocità). Dopo di che proviamo a trovare la soluzione solo per via grafica, utilizzando il diagramma spaziotempo di Galileo. Ci sembrerà di lavorare con un Minkowski molto più semplice. La motivazione? Sicuramente un aiuto per capire meglio Minkowski, ma anche per chiarirsi meglio le idee sulle differenze tra Galileo ed Einstein.

Un esercizio che possono seguire tutti con estrema facilità, dato che l'unica cosa che serve sapere è la formula che definisce la velocità:

v = s/t     (velocità uguale allo spazio percorso in un certo tempo).

Utilizziamo un paio di treni, un palo della luce e una casetta lungo la ferrovia e poniamoci quattro problemi, raffigurati nella Fig. 1, dall'alto verso il basso

Il primo vede coinvolti un treno di lunghezza L₁ e velocità v₁ e un palo della luce; il secondo lo stesso treno e una casetta ai bordi della ferrovia di lunghezza D; il terzo considera il nostro treno che ne supera uno di lunghezza L₂, che viaggia nello stesso verso del primo con velocità v₂ < v₁ : il quarto è come il terzo, ma con il secondo treno che viaggia in verso opposto al primo.

La domanda è sempre la stessa: quanto tempo impiega il nostro treno 1 (rosso) a oltrepassare completamente il secondo  "intruso"?

Seguiamo prima l'approccio matematico...

Treno e palo della luce

La Fig. 2 ci aiuta a comprendere il banale calcolo da fare:

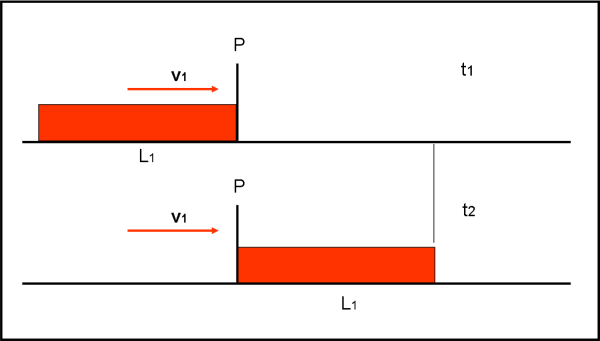
In alto la testa del treno arriva in linea col palo P (tempo t₁). E' necessario che tutto il treno superi il palo fino a giungere alla seconda situazione(tempo t₂). Il tempo necessario al treno per superare il palo è dato da Δt = t₂-t₁. La velocità del treno è v₁, mentre la lunghezza da percorrere è data dalla lunghezza del treno L1. Basta allora scrivere la formula della velocità:

v₁ = L₁/Δt

E, di conseguenza:

Δt = L₁/v₁

A parole: il tempo richiesto è quello necessario a percorrere la lunghezza L₁ andando alla velocità v₁.

Treno e casa

Usiamo la Fig. 3.

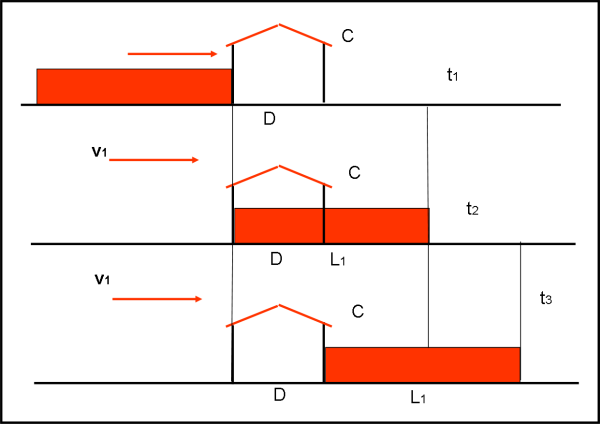
Al tempo  t₁ la testa del treno giunge al limite sinistro della casa. Al tempo t₂ il treno ha oltrepassato completamente il limite sinistro della casa (ossia ha percorso uno spazio pari alla sua lunghezza L1). La faccenda non è ancora conclusa. E' necessario che la coda del treno superi il limite destro della casa, ossia deve ancora percorrere uno spazio pari alla lunghezza della casa D (tempo t₃).

Il tempo totale è allora dato da

Δt = (t₃ - t₂) + (t₂ - t₁)

t₂ - t₁ è il tempo necessario per percorrere la lunghezza L1, ossia:

t₂ - t₁ = L1/v₁

t₃ - t₂ è il tempo necessario per percorrere la lunghezza D, ossia:

t₃ - t₂ = D/v1

Da cui

Δt = (t₃ - t₂) + (t₂ - t₁) = L1/v₁ + D/v₁ = (L1 + D)/v₁

A parole: il tempo richiesto è quello necessario a percorrere la lunghezza L1 + D, andando alla velocità v₁.

Due treni nello stesso verso

Il problema è simile a quello precedente con la sola differenza che la casetta è diventata un treno che si sposta in avanti con una velocità v₂.  Usiamo la Fig. 4:

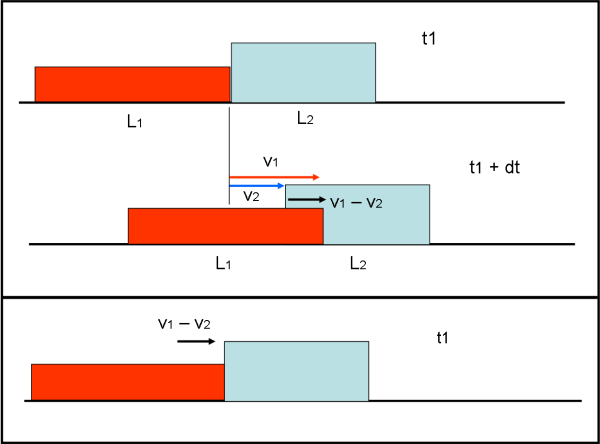
Al tempo t₁ il treno rosso raggiunge la coda del treno azzurro (più lento). In un certo tempo dt il treno rosso si muove di

ds₁ = dt v₁

mentre il treno azzurro si muove di

ds₂ = dt v₂

Ne segue che nel tempo dt il treno rosso è riuscito a sorpassare il treno azzurro soltanto di una lunghezza pari a:

ds₁ - ds₂ = dt(v₁ - v₂)

Percorrere ds₁ - ds₂ in un tempo dt è come dire  viaggiare con una velocità v₁ - v₂

(v₁ - v₂) = (ds₁ - ds₂)/dt

In parole povere, considerando il treno azzurro fermo, il tempo necessario a superarlo da parte del treno rosso sarà identico al caso della casetta precedente (ferma), imponendo, tuttavia, che la sua velocità si sia ridotta a v₁ - v₂ (parte bassa della figura). Non facciamo altro che porci nel sistema di riferimento del treno azzurro (con Galileo si può fare...).

Ne segue che il treno rosso impiega un tempo totale dato da (vedi caso della casetta):

Δt = (L1 + L2)/(v₁ - v₂)

Due treni in verso opposto

Il problemino si risolve come quello precedente, ragionando velocemente sulla somma delle due velocità (Fig, 5):

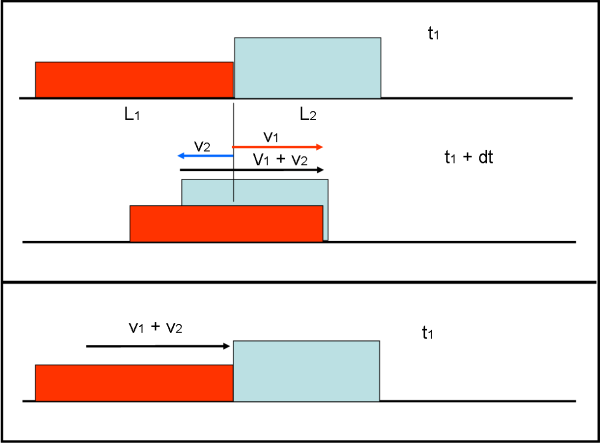
Il treno rosso percorre un certo spazio ds₁ in un tempo dt. Nello stesso tempo, però, il treno azzurro si sposta di ds₂ verso sinistra, velocizzando così la sua copertura da parte del treno rosso.  Nel tempo dt lo spazio percorso dal treno rosso sarà quindi dato da:

ds₁ + ds₂ = dt(v₁ + v₂)

Percorrere ds₁ + ds₂ in un tempo dt è come dire viaggiare con una velocità v₁ + v₂.  Questo risultato ci permette di  considerare il treno azzurro fermo e la velocità di quello rosso uguale a v₁ + v₂. Il tempo necessario a superare il treno azzurro, diminuisce e diventa:

Δt = (L1 + L2)/(v₁ + v₂)

Entriamo nello spaziotempo galileiano

Una serie di soluzioni veramente banali (si poteva anche concludere più velocemente). Tuttavia, voglio mostrare come si può arrivare allo stesso risultato per via puramente grafica, portandoci nello spaziotempo galileiano, ricordando che il tempo appare sempre lo stesso in ogni sistema di riferimento.

Treno e palo

Consideriamo in Fig. 6 il diagramma spaziotemporale della configurazione.

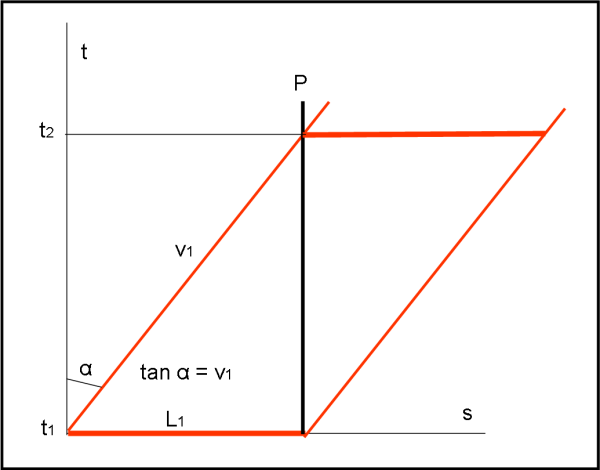
All'istante t₁ il treno di lunghezza L1 ha la testa a contatto con il palo P. Il suo tragitto spaziotemporale è indicato dalle due linee oblique equidistanti, inclinate rispetto all'asse t di un angolo la cui tangente è proprio la velocità v₁. Il palo P si muove solo lungo il tempo t e ne consegue che il treno lo passa completamente solo quando è tutto a destra della sua linea temporale verticale. Il tempo del passaggio è quindi leggibile direttamente sul grafico come t₂ - t₁.

Treno e casetta

Nella Fig. 7,  il treno ha il primo contatto con la casetta in t₁. In t₂ ha percorso la sua lunghezza L1 e la  coda ha raggiunto il limite sinistro della casetta. In t₃ anche la coda del treno lascia la casetta. Il tempo totale è t₃ - t₁.

Due treni nello stesso verso

In Fig. 8, il treno rosso, più veloce, ha delle traiettorie spaziotemporali più inclinate di quelle del treno azzurro.

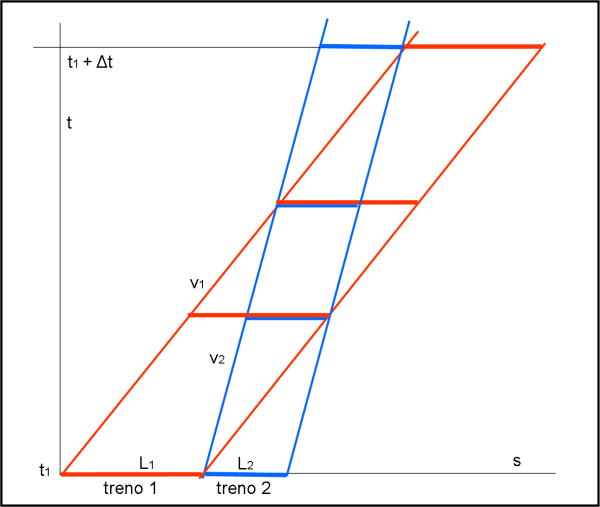
Ne segue che, mentre il rosso si muove, lo fa anche il treno azzurro, cercando di scappargli... Ovviamente, alla fine, il treno rosso riuscirà a passare il treno azzurro, ma ci metterà più tempo rispetto al tempo necessario a superare una casetta ferma. Il tempo totale Δt si disegna facilmente. così come si possono evidenziare i vari eventi precedenti (primo contatto testa-coda, contatto testa-testa; contatto coda-coda; contatto coda-testa) seguendo passo passo il sorpasso.

Due treni in verso opposto

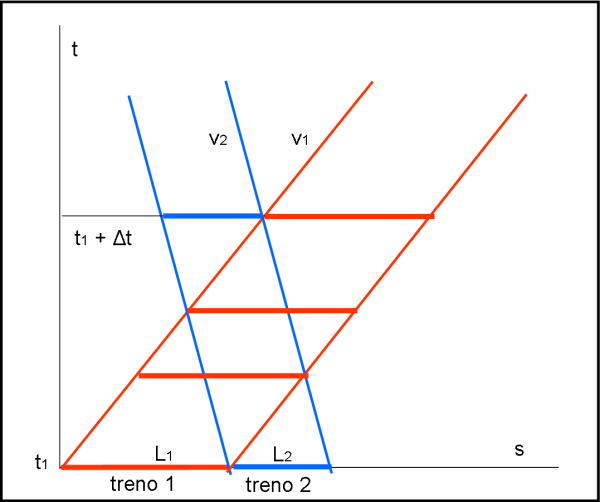
In Fig. 9, la traiettoria del treno azzurro è ribaltata e si getta nelle braccia del treno rosso. In qualche modo sveltisce i tempi e facilita il sorpasso completo. Come nel caso precedente si evidenziano molto bene i vari eventi più importanti.

Una considerazione generale: e' chiaro che in questi casi veramente banali la soluzione grafica diventa un specie di gioco fine a se stesso. Tuttavia, la trattazione che ne deriva aiuta a entrare nel mondo più complicato di Minkowski.

Tanto per continuare a giocare, qualcuno potrebbe dirmi: "Ma il risultato ottenuto analiticamente è veramente lo stesso di quello grafico?". Possiamo accontentarlo subito, utilizzando la Fig. 10(a,b).

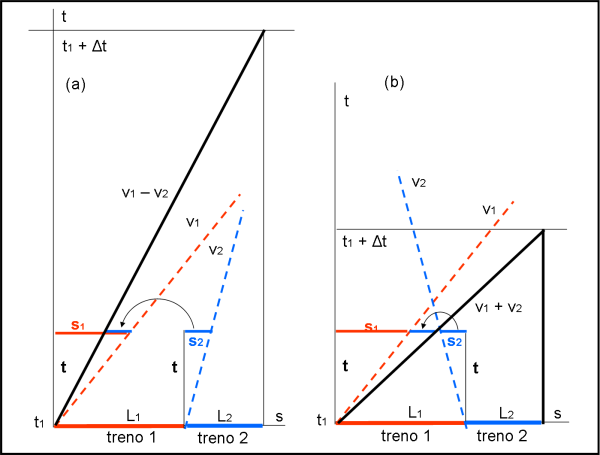
Manovrando con i triangoli atti a definire la velocità dei due treni è immediato sottrarle, ottenendo la velocità differenza tra le due (v₁ - v₂), nel caso (a):

v₁ = s₁/t

v₂= s₂/t

v₁ - v₂ = (s₁ - s₂)/t

Nel caso (b) è altrettanto facile sommare i due segmenti orizzontali e ottenete la somma delle velocità (v₁ + v₂).

Basta poi considerare l'intersezione tra la traiettoria spaziotemporale del'ipotetico treno con velocità ridotta (e aumentata), con la retta verticale a distanza L1 + L2 rispetto all'origine. Controllate pure... il risultato è ovviamente lo stesso.

Ci sono sicuramente altri metodi grafici per arrivare alla stessa soluzione... Com'è bello lo spaziotempo galileiano... No, non illudetevi torneremo presto a Minkowski.

QUI una favola che affronta, in modo molto elementare e divertente, le differenze tra la relatività di Galileo e quella di Einstein.