Questo articolo è stato inserito nelle sezioni d'archivio "Matematica e Geometria" e "Storia della Scienza"

La matematica, e la statistica in particolare, fanno uso di tante versioni di “media” di una  serie  di valori numerici. Noi tratteremo le quattro più comuni, di cui tre sono chiaramente riconducibili al grande Pitagora e alla sua scuola. Non per niente per stabilirne la correlazione è più che sufficiente il suo teorema. Un articolo veramente per tutti.

Ciò che vogliamo fare in questo articolo estremamente semplice è quello di confrontare tra di loro vari tipi di media, solo e soltanto attraverso un approccio geometrico che probabilmente era ben conosciuto ai tempi dell’antica Grecia. Ovviamente, oggi vi sono tantissimi metodi matematici per ottenere lo stesso risultato, ma l’eleganza geometrica pitagorica è troppo affascinante per non seguirla.

Definiamo le quattro “medie” che vogliamo trattare…

Media aritmetica

E’ quella più comunemente usata per stabilire il valore medio di una certa serie di misure. Può essere definita facilmente come la somma dei valori numerici diviso il loro numero. Ovviamente, sono ammessi sia valori negativi che positivi.

M_ari = (x₁ + x₂ + x₃ + …. + x_n)/n

Media geometrica.

Essa si applica soprattutto quando le grandezze in gioco devono moltiplicarsi tra loro. Viene definita come la radice ennesima del prodotto di n valori numerici. Contenendo un prodotto, non ha significato quando un valore è uguale a zero e non viene applicata a numeri negativi in quanto potrebbero portare a radici pari negative.

M_g = (x₁· x₂· x₃·….· x_n)^1/n

Come esempio potremmo considerare l’area di un rettangolo di lati a e b. Vorremmo ottenere il valore medio del lato di un quadrato che abbia la stessa area del rettangolo. Ebbene, facendo la media aritmetica dei due lati otterremmo (a = 4, b = 2)

M_ari = (4 + 2)/2 = 6/2 = 3

Ma un quadrato di lato 3 ha un’area pari a 9, mentre quella del rettangolo è soltanto 8.

Facendo la media geometrica tra i due lati avremmo invece:

M_g = (ab)^1/2 = (4·2)^1/2 = 2·√2

Questo è il valore cercato, infatti:

(2 ·√2)² = 8 (area quadrato che ha per lato la media geometrica dei lati del rettangolo)

Media armonica

Il nome deriva da un concetto importantissimo per i greci, legato alle note della lira e alle rispettive corde. Dobbiamo sempre imparare da loro per come problemi puramente matematici o geometrici avevano sempre un collegamento con molte altre discipline: una visione del mondo completa e non ridotta a specializzazioni spesso troppo chiuse in se stesse.

Dati n valori numerici, essa si definisce come il rapporto tra il numero n e la somma dei reciproci dei valori numerici.

M_arm = n/(1/x₁ + 1/x₂ + 1/x₃ + … +1/x_n)

In altre parole: è il reciproco della media aritmetica dei reciproci dei valori numerici.

Un esempio della sua applicazione riguarda la velocità media.  Se un corpo si muove da A a B, che distano 80 km, alla velocità di 80 km/h e successivamente da B ad A alla velocità di 20 km/h, quale sarà la velocità media sull'intero tragitto di andata e ritorno? Se si facesse la media aritmetica delle due velocità si otterrebbe 50 km/h.

M_ari = v_M = (80 + 20)/2 = 50 km/h

Questo sarebbe un valore errato. Bisogna, infatti,  notare che l'intero tragitto è di 160 km, e che viene percorso in 5 ore (1 all'andata e 4 al ritorno): la velocità media corretta (lunghezza del percorso divisa per il tempo impiegato a percorrerlo) è dunque:

v_M = 160/(1 + 4) = 160/5 = 32 km/h

Valore che corrisponde esattamente alla media armonica:

v_M =2/((1/80) + (1/20)) = 2/(20 + 80)/1600 = 3200/100 =32 km/h

Le tre medie considerate sono anche dette medie pitagoriche.

Vogliamo aggiungerla un’altra, dato che è facilmente collegabile alle prime tre…

Media quadratica

Essa ha il vantaggio di poter essere usata anche per valori negativi, di cui non interessi il segno. E’ quella più sensibile ai valori che si discostano dal valore centrale della serie. Essa è definita come segue:

M_q = ((x₁² + x₂² + x₃² + …. + x_n²)/n)^1/2

Date queste definizioni non è molto difficile capire che si utilizzano  a seconda del tipo di risultato si vuole ottenere. Tuttavia, in generale, tra loro esiste una relazione ben definita:

M_q ≥ M_ari ≥ M_g ≥ M_arm

Noi vogliamo proprio dimostrare questa relazione rifacendoci ai grandi pitagorici e utilizzando solo il teorema di Pitagora. Una dimostrazione puramente geometrica.

Per semplicità (ma è banale generalizzare l’esempio in modo aritmetico) useremo solo due valori numerici e, attraverso una semplice traslazione, dimostreremo anche che il segno uguale vale solo e soltanto quando  i due valori sono uguali. Tradotto in modo più intuitivo:

((a² + b²)/2)^1/2 ≥ (a + b)/2 ≥ (ab)^1/2 ≥ 2/(1/a + 1/b)

Cominciamo a fare una  prova numerica (meglio verificare…), con a = 3 e b = 7

5.39 > 5.00 > 4.58 > 4.20

Bene, possiamo cominciare, considerando, in Fig.1, due segmenti consecutivi di lunghezza 3 e 7 lungo l’asse orizzontale (OA in rosso e AB in blu). Disegniamo facilmente il semicerchio di raggio (a + b)/2 centrato in C (punto di mezzo di OB). Tracciamo dal centro il raggio verticale CV e lo coloriamo in nero. Beh… esso rappresenta la prima media, quella aritmetica e lo chiamiamo M_ari.

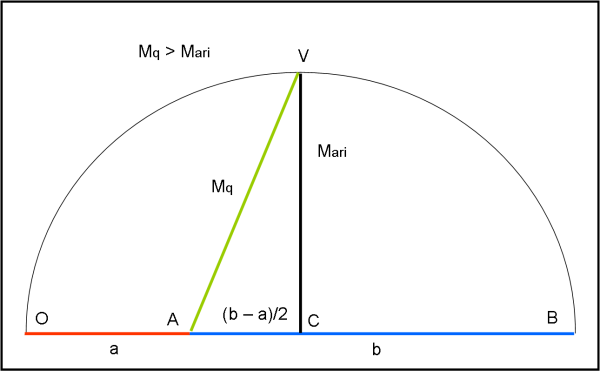
A partire da A tracciamo il segmento AV (verde). Ci vuole ben poco a dimostrare che AC è uguale a (b – a)/2. Infatti;

AC = OC – OA = (a + b)/2 – a = (a + b – 2a)/2 = (b – a)/2

Il triangolo ACV e  rettangolo per costruzione ed è immediato calcolare la sua ipotenusa applicando il teorema di Pitagora:

AV = ((b + a)²/4 + (b – a)²/4)^1/2 = ((b² + a² + 2ab + a² + b² - 2ab)/4)^1/2 = (2(a² + 2b²)/4)^1/2

E quindi:

AV = ((a² +b²)/2)^1/2 = M_q

Essendo Mq l’ipotenusa deve per forza essere

M_q > M_ari

Passiamo alla Fig. 2.

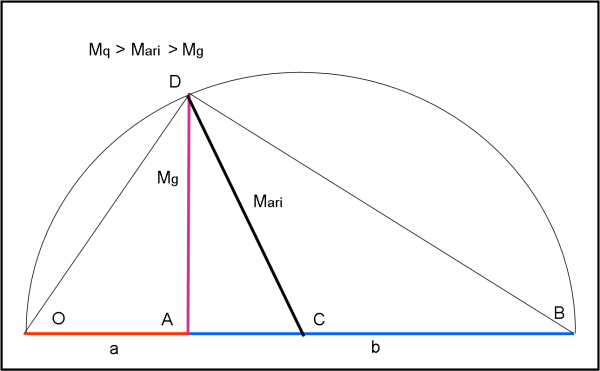
Dal punto A tracciamo la verticale fino a incontrare il cerchio in D (AD viola). L’angolo in D deve essere rettangolo dato che AB è il diametro del cerchio. Possiamo perciò applicare il secondo teorema di Euclide (sempre lui!) al triangolo ODB. Esso dice: “In un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa”. Tradotto in simboli matematici:

AD² = OA · OB =  ab

AD = (ab)^1/2 = M_g

Tracciamo il segmento DC che altro non è che il raggio del cerchio, ossia M_ari. Il triangolo DAC è rettangolo, per cui un cateto deve essere sempre minore dell’ipotenusa, da cui segue:

M_ari > M_g

Disegniamo, adesso, la Fig. 3 in cui consideriamo nuovamente il triangolo rettangolo DAC.

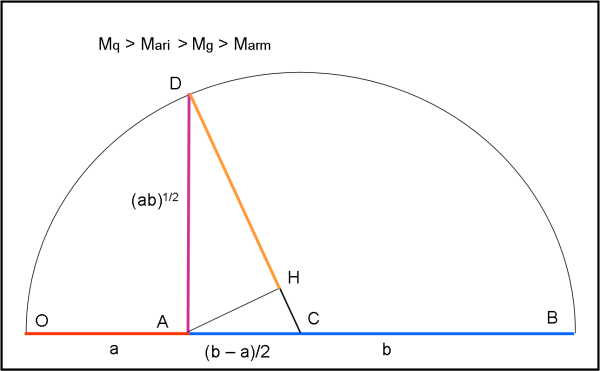
Dal punto A tracciamo la perpendicolare AH all’ipotenusa. I due triangoli DAC e DHA sono simili (entrambi rettangoli e con l’angolo in D in comune), per cui si può scrivere:

DH/AD = AD/DC

DH · DC = AD²

DH = AD²/DC

DH = ab/((a + b)/2) = 2ab/(a +b) = 2/((a + b)/ab) = 2/(1/a + 1/b) = M_arm

Ma DH  (colorato in arancione) è il cateto di un triangolo che ha Mg come ipotenusa (DHA), per cui ne segue che:

M_g > M_arm

Abbiamo perciò ottenuto per via puramente grafica e usando solo il teorema di Pitagora (quello di Euclide ne è una derivazione immediata) la diseguaglianza voluta:

M_q  > M_ari  > M_g  > M_arm

In Fig. 4 riportiamo i 4 segmenti corrispondenti alle 4 medie considerate.

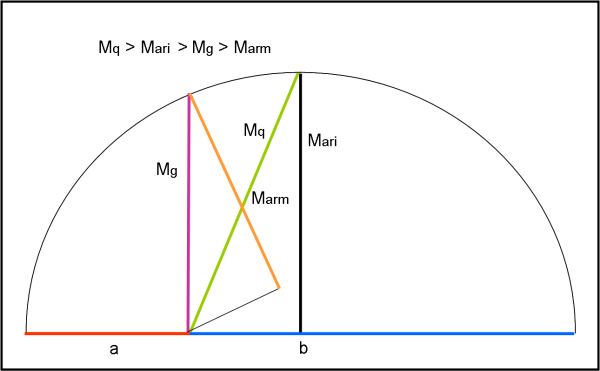
E’ anche immediato mostrare come la diseguaglianza diventi un’uguaglianza se e solo se a = b.

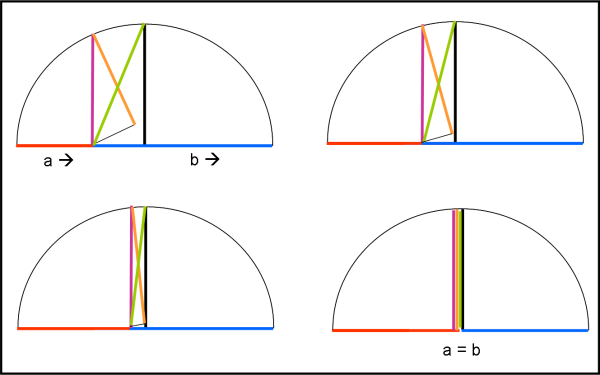
Ce lo mostra in quattro passaggi la Fig. 5, dove da sinistra a destra e dall’alto in basso abbiamo allungato  a e accorciato b fino a renderli uguali: le quattro medie coincidono perfettamente.

Ovviamente, vi sono vari metodi per dimostrare la diseguaglianza delle medie, ma quello usato è veramente alla portata anche di chi ama poco la matematica…