Categorie: Fisica classica
Tags: cinematica unidimensionale moti pietra quiz velocità
Scritto da: Vincenzo Zappalà
Commenti:18
Quiz cinematico sulla pietra che va su e giù **
Un problema di cinematica a una dimensione, di moderata difficoltà, che permette, però, di introdurre (e ricavare) una formula che non è usata molto spesso. Ciò non toglie che esistano altri metodi di soluzione. Anche questo è stato presentato in una Università, addirittura in quella di Adelaide
Da un punto A posta una certa altezza L , viene lanciata una pietra verticalmente verso l'alto. Quando la pietra torna indietro e raggiunge una distanza h rispetto al punto A, verso il basso, la sua velocità è doppia rispetto a quando aveva raggiunto un'altezza h sopra il punto A. Si chiede: "Qual'è la massima altezza H raggiunta dalla pietra in funzione della sola h?"
La massima altezza si misura a partire da... ?
Ovviamente L deve essere maggiore di h, ma poco importa il valore di L ...
La risposta :"La pietra non può scendere di h, dato che prima incontra la testa di A (come nella figura di copertina) NON E' VALIDA!"
18 commenti
H rispetto al punto A o rispetto al riferimento della sua altezza L ? Cioè, nella formula finale , a primo membro deve comparire H oppure H-L ?
Per ora ho calcolato che la quantità H-L , con i dati del problema, è pari a 5/3 h.
Caro Artù, L non conta niente... l'ho solo messo maggiore di h per dire che la pietra può tranquillamente scendere di h rispetto al punto A senza toccare terra...
nel testo c'è anche scritto che deve essere funzione di h... non è abbastanza chiaro? Lo scrivo meglio...
Ok, ma l'H cercata (massima altezza raggiunta) è riferita al punto A (da cui la pietra comincia a salire) o al suolo (rispetto al quale il punto A ha un'altezza di L) ? Non mi è chiara questa cosa.
Beh... nel moto considerato quella che conta è l'altezza rispetto a qualcosa di ben preciso, dato che L può essere qualsiasi e non vogliamo che compaia...
Ma non è difficile inserire anche L, qualsiasi esso sia...
Allora, se per massima altezza raggiunta intendiamo quella rispetto al punto A, da cui la pietra è stata lanciata verticalmente verso l'alto, confermo la mia risposta data prima: 5/3 h . A questo risultato sono arrivato utilizzando una delle leggi del moto uniformemente accelerato , non so se il riferimento è a questa a proposito della poca frequenza con cui viene usata:
dove v2 è la velocità finale del tratto di traiettoria considerato, v1 la velocità iniziale , a l'accelerazione ed lo spazio percorso tra la posizione iniziale e quella finale. Nel nostro caso, come punto iniziale del tratto di traiettoria prendo quello in cui la pietra si trova a distanza h sopra il punto A e come punto finale quello in cui la pietra si trova a distanza h sotto il punto A. Chiamo , per favorire la comprensione, C il punto iniziale e D quello finale. Nel nostro caso, inoltre, l'accelerazione è ovviamente quella di gravità e lo spazio s percorso è pari a 2h. La suddetta relazione, quindi, si trasforma in:
Il problema, inoltre, offre come dato :
vd=2 vc
per cui, sostituendo , ottengo:
da cui, esplicitando rispetto a vc:
Ricordando, ora, la formuletta che mi restituisce la velocità di caduta di un grave da una altezza h' (per distinguerla da h)
e confrontandola con la (1), posso dedurre che quando la pietra si trova nel punto C è caduto per una altezza h' pari a 2/3 h. In altre parole, la distanza tra il punto di massima altezza e il punto C è 2/3 h. Poichè, inoltre, la distanza verticale tra C ed A è, come dato del problema, pari ad h, allora la massima altezza raggiunta , misurata dal punto A, sarà pari a h + 2/3 h cioè 5/3h.
C.V.D.
Ciao, io avevo ragionato con la conservazione dell'energia : energia potenziale gravitazionale + energia cinetica = costante.
In un diagramma v2 (che prendo come ascisse) e z (quota che prendo come ordinate), con origine in v2=0 e z=0 (per comodità lo prendo nel punto più basso) la legge di conservazione è una retta che deve passare per i seguenti punti :
(0;H) punto più alto
(v12;2h) punto sopra il lancio
(v02;h) punto di lancio
(v22;0) punto di arrivo, che corrisponde a (4v12,0)
I 4 punti devono giacere su una stessa retta, da cui si dovrebbe ricavare H in funzione di h
Non ho però fatto calcoli, che non ho modo di scrivere.
Ciao
Opss:ho visto che gli apici 2 sono stati messi in linea anziché come quadrato
dammi almeno il risultato.. Francesco, grazie!
Avevo scelto anch'io il metodo energetico, con un po' la paura di finire fuori tema. Se devo essere sincero, non conoscevo la formula citata da Arturo, che proviene da manipolazioni delle formule fondamentali del M.U.A.
Visto che Francesco ha tirato in ballo il discorso energetico, ma forse non riesce a scrivere le formule con Latex o altro, mi permetto di esplicitare il discorso.
Ragionando sull'energia, e chiamando V1 la velocità in h sopra L, V2 la velocità in h sotto L, si ha:
calcoliamo adesso il tempo impiegato a raggiungere la velocità V1, che chiamiamo t1; In M la velocità iniziale è zero, sappiamo poi che in generale nel M.U.A. v=at se la velocità iniziale è zero. Quindi t1=v/a
Nel nostro caso , essendo a=g,otteniamo: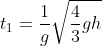
; Lo spazio percorso da M per arrivare all' h sopra è pertanto
grazie Umberto!!!!
Sto scrivendo al cellulare, quindi scusatemi.
H=8/3h
(a lettere H uguale a 8/3 h)
caro Francesco,
devi avere commesso qualche errore di calcolo... il risultato non è giusto. Controlla bene ogni passaggio, appena puoi
È molto probabile. Però, senza fare calcoli, se il punto più basso lo mettiamo quota zero, il punto di lancio è quota h, il punto dove la velocità è metà di quella finale è 2h, il punto più alto (con velocità nulla) e H. Ora H deve essere necessariamente maggiore di 2h (altrimenti per 2h la pietra non ci passa). Quindi H>2h. Ma se mi dici che H=5/3h, vuol dire che abbiamo quota zero differente.
Scusami, ma essendo su un cellulare con uno schermo mini, leggere i passaggi degli altri mi risulta difficile e non riesco a vedere il loro zero.
Ok, rileggendo al pc, vedo che si parla di H sopra L, quindi diciamo la stessa cosa (il fatto che ci fosse un 3/3h di differenza mi ha insospettito).
H è 5/3h sopra il punto di lancio, cioè 8/3h sopra il punto finale.
La massima altezza si misura a partire da...? Dipende dall'osservatore (per me quello privilegiato è l'osservatore che prende in testa la pietra)
Ciao
Solitamente, come avevo già scritto in un commento, l'altezza si misura dal punto di partenza. Comunque, al limite sarebbe 5/3h + L, con L incognito e qualsiasi...