Come definire il caos? Normalmente si pensa a qualcosa senza regole e disordinato oppure a qualcosa di imprevedibile. Tuttavia c’è caos e caos, non ultimo il caos deterministico, una definizione che sembra negare se stessa. Un articolo piuttosto lungo (ma non certo difficile) che preferisco pubblicare tutto insieme per non interrompere lo svolgimento di un’avventura che non può che entusiasmare.

La parola caos si usa sovente, nel linguaggio comune, con il significato di disordine, di oggetti messi a caso. Ben diverso è il significato matematico. Le dinamiche caotiche non sempre sono legate a variabili casuali, probabilistiche o nascoste. Il problema più frequente per la soluzione di una certa evoluzione nel tempo sta proprio nelle condizioni di partenza. Se il sistema è semplice si può anche partire con dati abbastanza approssimativi e si è sicuri che il risultato finale manterrà una certa incertezza ma non si discosterà molto da un risultato abbastanza ben definito. La situazione può invece essere più complessa, tale che il più piccolo errore commesso nell’inserire i dati iniziali può portare a soluzioni del tutto imprevedibili e completamente diverse tra loro.

Ci sarebbero molte considerazioni da fare su come il concetto di caos sia stato affrontato durante la storia dell’uomo. Basti pensare che lo stesso Aristotele diceva: “La minima deviazione dalla verità viene poi moltiplicata migliaia di volte in seguito”.

Esempio classico di caos è sicuramente il problema dei tre corpi, dove, pur conoscendo tutte le variabili in gioco, basta un infinitesimo errore su una sola di esse per far cambiare drasticamente il risultato finale.

Abbiamo già parlato di caos e della definizione che grandi scienziati hanno cercato di applicargli (QUI).

Tuttavia, in tempi piuttosto recenti si è manifestato  un tipo di caos, il cui stesso nome è formato da due parole di significato opposto (un vero ossimoro). Esso prende il nome di CAOS DETERMINISTICO.  In parole semplici, la parola deterministico riporta a un fenomeno che attraverso un modello matematico permetta di trovare una soluzione unica e quindi del tutto prevedibile, mentre la parola caos sta proprio a indicare l'opposto, cioè un risultato del tutto imprevedibile.

Chi non conosce l’effetto farfalla? L'attrattore di Lorenz fu il primo esempio di un sistema di equazioni differenziali a bassa dimensione, in grado di generare un comportamento caotico. Venne scoperto da E. N. Lorenz, del MIT, nel 1963. Non si sa bene se la definizione così poetica e ultra-sfruttata derivi dal titolo di una sua conferenza del 1972 (“Può, il batter d'ali di una farfalla in Brasile, provocare un tornado in Texas?”) o dalla forma delle sue soluzioni rappresentate nello spazio delle fasi, dall’aspetto estremamente simile a una farfalla.

Noi non vogliamo certamente entrare a fondo nell’esperimento di Lorenz (problema a tre dimensioni di non facile esposizione) e ci limitiamo a un esempio molto più semplice, ma altrettanto interessante, descrivibile con una semplice equazione di secondo grado.

Il problema che vogliamo affrontare viene spesso associato allo sviluppo di una popolazione, ma potrebbe essere esteso a moltissime altre evoluzioni, soprattutto finanziarie.

Siamo di fronte a ciò che si definisce sistema dinamico. Un qualsiasi sistema dinamico si compone di due parti: le variabili caratteristiche del suo stato (cioè le informazioni essenziali sul sistema) e la dinamica (una regola che descrive l'evoluzione dello stato nel tempo).

Cominciamo a considerare un’equazione lineare, dimostrando che essa non porta a caos e può ancora avere senso la frase: un sistema dinamico lineare che parta con un piccolo errore nelle condizioni iniziale porta a errori finali ancora relativamente piccoli. Ciò non sarà più vero per un sistema dinamico semplice non lineare (senza inserire nessun termine esponenziale). Il percorso è stato tracciato da Robert May, nel suo articolo del 1976, dal titolo molto esplicito: Semplici modelli matematici con dinamiche molto complicate.

Consideriamo, dapprima, una situazione oltremodo semplice che abbia, comunque, una certa logica di base…Ammettiamo che esista una popolazione di insetti e che si voglia studiarne l’evoluzione, imponendole qualche regola.

Evoluzione lineare di insetti

A un certo istante t, il loro numero sia x(t). Immaginiamo che una parte di  essi si riproduca ad ogni stagione e che il numero dei nuovi nati sia una frazione n di quelli esistenti. Alla popolazione x(t) dobbiamo aggiungere un fattore nx(t). Nel frattempo, però, qualche insetto muore e il numero di morti per stagione è pari a una frazione m della popolazione. Al valore x(t) dobbiamo perciò anche togliere un fattore mx(t). Mettendo tutto assieme, possiamo scrivere la popolazione al tempo t+1:

x(t+1) = x(t) + nx(t) – mx(t)

x(t+1) = (1 + n - m) (x(t)

poniamo k = 1 + n - m

e otteniamo:

y = x(t +1) = k x(t)                    …. (1)

Una semplice equazione di primo grado che dà luogo a una “mappa” evolutiva estremamente semplice da rappresentare.

Nel caso che n > m, abbiamo un valore di k maggiore di 1. Ad esempio, considerando la popolazione iniziale uguale a 10 e k uguale a 1.5, possiamo facilmente calcolare la crescita della popolazione in funzione del tempo, scrivendo pochi numeri calcolati con la (1).

La sequenza di valori della y per tempi successivi sarà 15, 22, 34, 51, 76, 114, …, avendo ovviamente approssimato all’insetto “intero”. L’andamento della popolazione è mostrato in Fig. 1.

Se, invece, considerassimo m > n, avremmo k minore di 1 (sempre positivo, comunque) e la popolazione tenderebbe a zero. Divertiamoci a scrivere qualche numero anche in questo caso… partiamo da 100 individui per meglio vedere l’andamento e poniamo k = 0.5

La sequenza dei valori di y per tempi successivi unitari è data da 100, 50, 25, 12, 6, 3, 2, …, come riportato in Fig. 2

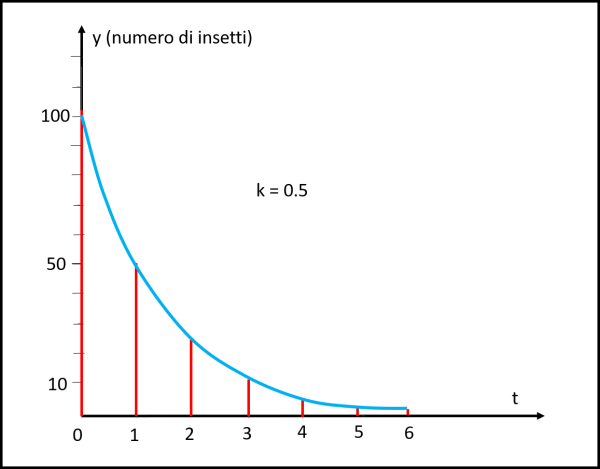
Abbiamo scritto e disegnato delle banalità, ma già possiamo dire che un piccolo errore nella popolazione iniziale non crea nessun problema al risultato finale. Si otterrebbero sempre infinito e zero per le due popolazioni soggette a questo certo tipo LINEARE di crescita o decrescita. Non solo, ma anche cambiando il coefficiente k si hanno solo due risultati ben definiti: per k maggiore di 1 (qualsiasi) abbiamo una popolazione che tende all’infinito; per k minore di 1 (qualsiasi) una popolazione che tende a zero. E’ solo questione di tempo…

Possiamo anche lanciarci in qualcosa di più generale: il punto O è un punto di equilibrio così come lo è, a modo suo, infinito. Essi sono anche quelli in cui la y si mantiene uguale a x. Essi possono essere stabili o instabili (attrattivi o repulsivi). Nel caso di k > 1 il punto zero è repulsivo, mentre infinito è attrattivo. Nel secondo caso (k < 1) il punto zero è attrattivo, mentre il punto all’infinito è repulsivo.

Qualcosa come la pallina e la scodella. Se mettiamo la scodella con la concavità verso l’alto, la pallina oscilla fino a fermarsi in fondo (attrazione), Se capovolgiamo la scodella, la pallina scapperà dalla cima e abbandonerà la scodella (repulsione). Nel primo caso il punto “fondo della scodella” è attrattivo, nel secondo caso è repulsivo.

In altre parole, nel primo caso possiamo anche partire da un valore di x molto lontano a un punto stabile (0), ma l’evoluzione lo farà  cadere sicuramente nel punto zero. Nel secondo caso, invece, possiamo prendere un valore vicinissimo a zero, ma l’evoluzione lo farà andare implacabilmente  sempre più lontano.

Nel caso in esame, quanto detto sembra un ragionamento un po’ forzato, ma vedremo che non lo sarà più nel caso successivo.

Per mettere le mani avanti, e vedere meglio quanto abbiamo detto, disegniamo un altro tipo di mappa, tralasciando il tempo e inserendo nel diagramma i valori correnti x(t) della popolazione (asse x) e i valori attesi per la stagione successiva x(t+1) (asse y).

Siamo di fronte a una relazione estremamente banale, dato che tutto si riduce alla relazione lineare del tipo

y = k x

Nient’altro che una retta… Tuttavia, cerchiamo di analizzare attraverso di lei quali sono i valori di y rispetto a x passo dopo passo, ossia stagione dopo stagione. Otteniamo lo stesso risultato di prima, ma usiamo un metodo di approccio che, benché del tutto inutile nel caso in esame, ci verrà molto utile in seguito.

Cominciamo con un valore di k maggiore di 1, ossia con una retta più inclinata della retta bisettrice del primo quadrante (y = x). Tracciamo questa retta, facendola partire dall’origine (popolazione nulla). Al primo passo inseriamo come x la popolazione attuale. La posizione successiva (y) si determina immediatamente portando la verticale da x fino a incontrare la retta y = kx. A questo punto prendiamo la y così ottenuta e la facciamo diventare la x successiva (la popolazione successiva è adesso diventata la popolazione corrente). Fatta questa operazione, tracciamo nuovamente la verticale dal valore della nuova x e andiamo a incontrare la retta che ci fornisce il valore di y, che a sua volta deve essere riportato sull’asse x per ottenere il nuovo y, e via dicendo… come mostrano le varie frecce e gli archi di cerchio di Fig. 3

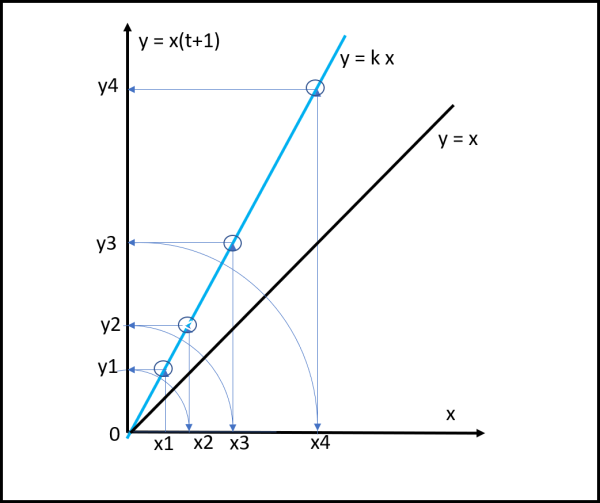
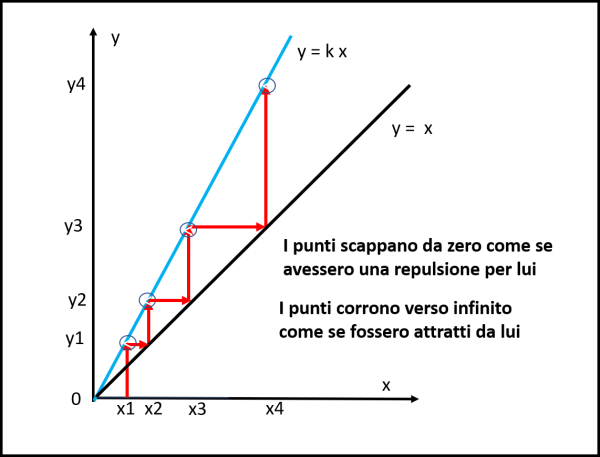
Beh… un bel lavoro, soprattutto... inutile. Si può fare molto più in fretta. Basta utilizzare  la retta y = x. La stessa formuletta ci dice cosa è capace di fare: definire una y esattamente uguale alla x e viceversa. Ma, allora, una volta trovata la prima y, basta andare verso destra fino a incontrare la retta y = x e nel punto di incontro sappiamo di avere una x uguale alla y, ossia abbiamo la x necessaria per il secondo passo. Si manda la verticale verso l’alto fino a incontrare la retta y = kx e otteniamo la nuova y che, trasportata in orizzontale fino alla retta y =x definisce la nuova x e via dicendo… Una specie di scaletta in cui i vari punti toccati della bisettrice prendono il posto delle x sottostanti, come mostra la Fig. 4.

E’ del tutto banale, fare la stessa identica cosa con un k minore di 1, come mostrato in Fig. 5. Questa volta si scende la scala e ci si avvia lentamente verso lo zero.

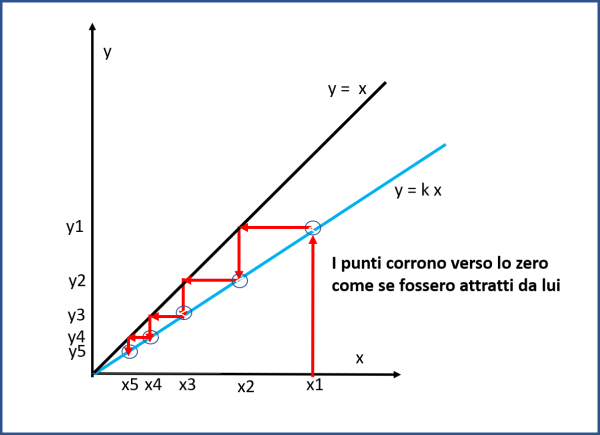
Ribadiamo che infinito e zero hanno proprio l’aspetto di due attrattori, il primo per k > 1 e il secondo per k < 1. Notiamo anche che essi sono anche i punti di intersezione (il primo per modo di dire…) tra la equazione dinamica y = k x e la retta y = x. Ci servirà in seguito.

Evoluzione non lineare degli insetti

Ovviamente, un'equazione lineare non può certo regalarci il caos, ma per incontrarlo basta rendere un po’ più complicata l’evoluzione degli insetti.

In realtà, abbiamo ipotizzato una vita troppo regolare, cosa che in Natura non può certo accadere. Facciamo un piccolo passo in più.

Ipotizziamo che l’aumento indiscriminato degli insetti provochi qualche problema e che causi una carenza di cibo tale da influire sulla mortalità. In poche parole, il parametro m non sia una costante, ma una funzione essa stessa del numero di insetti, ossia m = s x(t). Otteniamo l’equazione:

y = x(t+1) = x(t) + n x(t) – s x(t)x(t)

Imponiamo, per semplicità, che s = 1 + n

y = x(t+1) = x(t) + nx(t) – x(t)x(t) - nx(t)x(t)

y = x(t+1) = (1 +n) x(t)  – (1 + n) x(t)x(t)

y = x(t+1) = (1 +n) (x(t)  –  x(t)x(t))

y = x(t+1) = (1 + n) x(t) (1 – x(t))

Infine poniamo k = 1 + n e si ottiene la legge voluta

y = x(t+1) = k x(t) (1 - x(t))          …. (2)

Se il procedimento vi sembra troppo contorto, possiamo arrivare alla stessa equazione con un ragionamento ancora più semplice…

Partiamo da una relazione basata solo sulla crescita e scriviamo che

x(t+1) = k x(t)           …. (3)

Ossia, se c’è del cibo la popolazione aumenta della frazione n ad ogni stagione. Poi introduciamo un tasso di mortalità generico, legato al fatto che prima o poi il cibo mancherà. Basta dire che il rapporto tra x(t+1) e x(t) è proporzionale a x(t), ponendo come fattore di riduzione proprio – k. Otteniamo:

x(t+1)/x(t) = - k x(t)

x(t + 1) = - k x(t)x(t)              …. (4)

Tenendo conto di entrambi i fattori ( crescita e decrescita, (3) e (4)) si ha

x(t + 1) = kx(t) – kx(t)x(t)

y = x(t + 1) = k x(t)(1 – x(t))

Che è identica alla (2). Scegliete il ragionamento che preferite, dato che l’importante è lavorare sull’equazione di secondo grado trovata.

La relazione non è più lineare, ma rimane del tutto deterministica o, almeno, lo sembra…

La prima impressione ci fa pensare che anche questa volta troveremo un valore di equilibrio finale o, al più, che il risultato oscilli attorno ad esso (in fondo è quello che capita anche per i troiani nel problema dei tre corpi semplificato o per i punti lagrangiani in genere…).

Abbiamo scritto un processo che tende a favorire la crescita di una variabile, quando questa è caratterizzata da piccoli valori, e a bloccarne la crescita, quando il valore della variabile diventa troppo grande. Un’equazione davvero semplice, rappresentata da una parabola con la concavità rivolta verso il basso che passa per l’origine degli assi. Scriviamola per esteso:

y = x(t +1) = - k x(t)² + k x(t)       …. (5)

Si potrebbe addirittura pensare di ricavare l'espressione analitica che, partendo da x(0) ci permetta di calcolare direttamente x(t) con t qualsiasi. Vogliamo provare?

Non faremmo molta strada…

x(1) = - k x(0)² + kx(0)

x(2) = - k(-k x(0)² + kx(0))² + k (- k x(0)² + kx(0))

E siamo arrivati a un polinomio di quarto grado già al primo passaggio.

Non è difficile convincersi (basta provare) che al decimo passaggio il polinomio è già diventato di grado 1024!

No, no… è meglio abbandonare visto che il proposito è arrivare ad almeno qualche centinaio di passaggi. Meglio risolvere il tutto attraverso una mappa qualitativa come fatto precedentemente.

Possiamo anche limitare la variazione di k, mantenendola tra 1 e 4… è già più che sufficiente.

Siamo di fronte, come già detto a una legge evolutiva rappresentato da una parabola con la concavità verso il basso che passa per l’origine degli assi. Nell’asse x poniamo i valori della popolazione corrente e sull’asse y quelli della popolazione successiva. Ci ricordiamo, inoltre, il vantaggio che ci può dare il tracciare anche la retta y = x in modo da sveltire ogni singolo passaggio.

Possiamo anche dire qualcosa di più. L’intersezione tra la parabola e la retta y = x ci regala, per definizione, uno o due  punti di stabilità, dove, infatti, la popolazione successiva rimane la stessa di quella corrente. Nel caso lineare precedente quelle erano proprio le soluzioni finali. Nel caso attuale le due intersezioni sono date dal sistema:

y = - k x(t)² + k x(t)

y = x(t)

uguagliando le due espressioni

x(t) = - k x(t)² + k x(t)

k x(t)² + (1 - k) x(t) = 0

La prima soluzione è ovviamente

x(t) = 0

La seconda è:

k x(t) + 1 – k = 0

x(t) = (k - 1)/k         …. (6)

Questi due punti dovrebbero essere gli “attrattori” oppure i “repulsori”, che nel caso precedente lineare erano 0 e infinito.

Cominciamo a divertirci e prendiamo una parabola con k molto piccolo. Anzi, talmente piccolo che l’unico punto d’intersezione con la retta y = x sia l’origine.

La scelta di k non cambia i due punti in cui la parabola interseca l’asse x: l’intervallo è sempre 1. Quello che cambia è l’altezza del vertice della parabola.

Esso si trova sempre a x = ½ e quindi la sua altezza y_V è data da:

y_V = k (1/2) – k(1/4) = k/4

A tale scopo possiamo scegliere k = 1 , per il quale segue y_V = ¼ = 0.25, come mostrato in Fig. 6

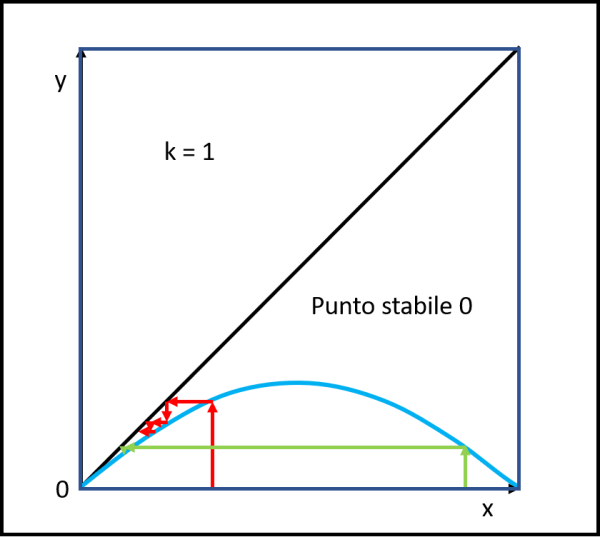
Da qualsiasi valore di x si parta, la “scaletta”, che abbiamo imparato a costruire nel caso precedente lineare, ci porta verso l’attrattore 0. E lo fa anche senza alcuna oscillazione.

Consideriamo adesso un caso in cui vi siano due intersezioni della parabola con la bisettrice, scegliendo, ad esempio, k = 2. L’ordinata y_V sarà uguale a 0.5. Vediamo la rappresentazione in Fig. 7. Non dobbiamo certo stupirci che  l’intersezione P tra retta e parabola (a parte l’origine) capiti proprio nel vertice della parabola. Basta considerare la (6) e si ottiene proprio

x(P) = (k – 1)/k =1/2, ossia proprio l’ascissa del punto di mezzo.

Disegniamo la Fig. 7 e partiamo pure da qualsiasi punto si voglia e la scaletta ci porta senza alcun problema verso il punto P = V in modo diretto. Ciò è vero anche per tutti i casi precedenti in cui 1 > k > 2. L’attrattore è diventato il punto P e gli insetti scappano velocemente da zero (punto repulsivo).

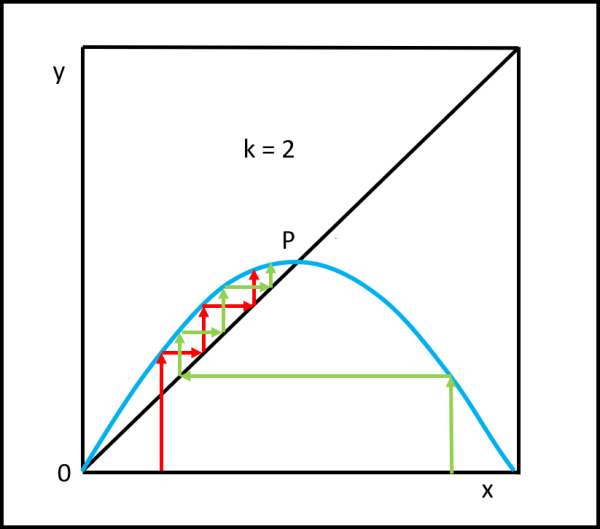
Andando oltre al valore k = 2, le cose cambiano solo apparentemente. Il punto P rimane punto di attrazione e di stabilità finale, ma adesso viene raggiunto “oscillandogli” attorno. Lo vediamo nella Fig. 8, dove abbiamo preso k = 2.7. La scaletta lo sorpassa e poi torna indietro avvicinandosi sempre di più fino a giungere in P. Una classica oscillazione smorzata. Se diamo tempo al tempo, ossia se lasciamo che i passaggi diventino veramente grandi, l’arrivo nel punto P è assicurato e P rimane soluzione stabile.

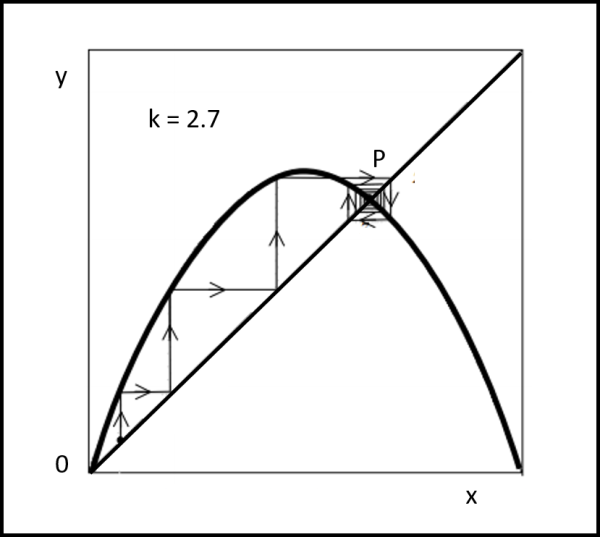
Sembra, in fondo, che l’equazione resti deterministica, pur lavorando in modo “qualitativo”.

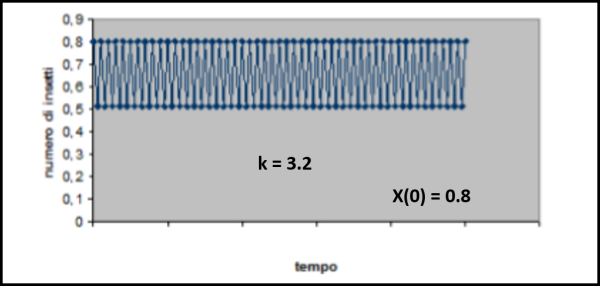
Le cose, invece, iniziano a cambiare drasticamente se superiamo il valore  k = 3. Proviamo con k = 3.2 (Fig. 9)

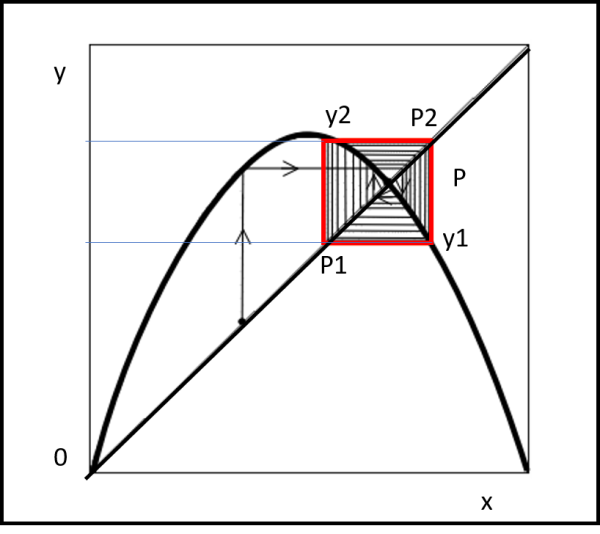
La scaletta sembra avvicinarsi al punto P, ma poi inizia a oscillare stabilizzandosi alla fine lungo la traiettoria rossa. Le soluzioni diventano 2 (P1 e P2). Le abbiamo segnate sulla retta y=x, dato che essa individua proprio i punti in cui la x è uguale alla y, per cui è immediato calcolare la popolazione corrispondente.  Ciò che abbiamo trovato  rappresenta una biforcazione, ossia i valori della popolazione (che possono essere rappresentati lungo la bisettrice dato che essa definisce la popolazione corrente e quella successiva) si stabilizzano su due valori diversi. L’oscillazione diventa periodica (periodo 2).

Possiamo vedere, in Fig. 10, la stessa situazione in un diagramma temporale, ossia inserendo i valori della popolazione di insetti al passare del tempo. All'inizio abbiamo un andamento transitorio che poi inizia a oscillare periodicamente tra due valori. Nel caso in esame è stato presa come popolazione di partenza x(0) il valore 0.8 e viene rappresentato l'andamento dopo il tratto iniziale transitorio. Siamo chiaramente di fronte a una oscillazione stabile periodica (periodo 2).

Aumentando k la situazione si complica ancora di più e in modo molto rapido. Ogni ramo della biforcazione si separa in due rami portando a 4 valori ripetitivi (periodo 4).

Per k = 3.5 la biforcazione si raddoppia e si raggiunge il periodo quattro, come mostra il diagramma temporale di Fig. 10.

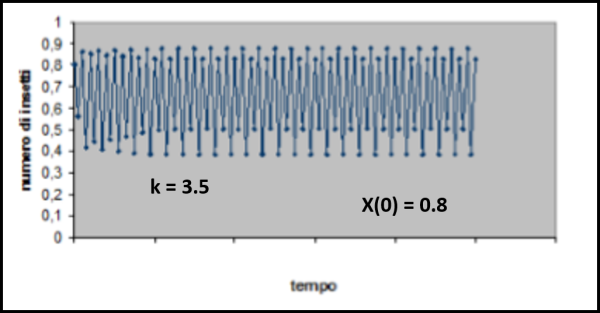
All'inizio del grafico si nota bene il passaggio dal periodo 2 al periodo 4.

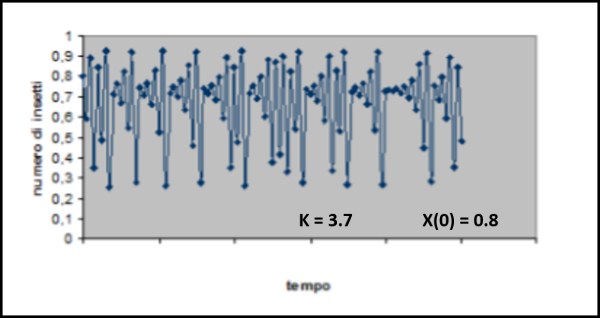
La faccenda evolve rapidamente e si ha una nuova biforcazione che porta a 8 valori (periodo 8 ) ma poi  il tutto diventa sempre più veloce e "complesso" e, superato il valore di 3.569, qualsiasi periodicità si perde in un regime del tutto caotico.  Guardiamo, in Fig. 11, la situazione per k = 3.7 con 440 iterazioni e ci rendiamo conto del “caos” ottenuto: non si raggiunge mai una situazione "stabile" di tipo periodico (o, almeno, questa è l'apparenza che oggi viene data alla situazione) e qualsiasi tentativo di previsione è del tutto impossibile.

Il diagramma temporale fa notare già molto bene come non esista più un andamento periodico (Fig. 12).

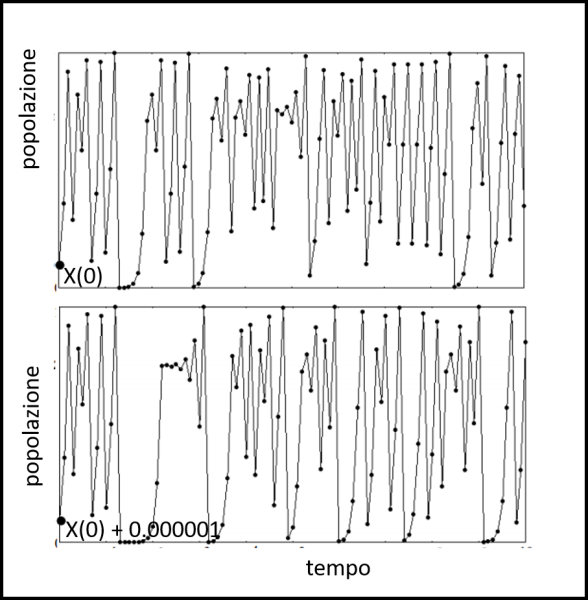
In questi casi diventa anche fondamentale dare la popolazione di partenza... È facile, infatti, verificare numericamente la sensitività rispetto alle condizioni iniziali, come mostrato nella Fig.13, dove la traiettoria in basso è stata ottenuta partendo da una condizione iniziale che differisce solo di un milionesimo, ovvero 0.000001, rispetto a quella rappresentata in alto. Come si può vedere, dopo le prime iterazioni, in cui si ottengono valori simili, le due traiettorie cominciano a differenziarsi sempre di più, fino a diventare completamente diverse. Non solo mancanza di periodicità, ma andamenti completamente "casuali" ... un vero caos deterministico!

E' sicuramente utile, per riassumere il tutto e evidenziarne meglio le caratteristiche, costruire un nuovo diagramma detto proprio diagramma di biforcazione.

Si riportano sull'asse orizzontale i valori del parametro k preso in un certo intervallo, ad esempio tra 2 e 4, e per ogni valore del parametro si calcolano i primi N punti della traiettoria, dove N è un numero sufficientemente grande (ad esempio N = 500). Sulla verticale passante per il valore di k utilizzato, si riportano i valori "asintotici" a cui tende il sistema, ossia quelli più avanti fra quelli calcolati, una volta eliminata la parte transitoria. Il diagramma viene riportato nella Fig. 14, dove è facile notare come si susseguano sempre più rapidamente, al crescere di k, i successivi raddoppi del periodo : da 2 a 4 a 8, poi a 16, 32, ... e tutta la successione delle potenze di 2 fino a un valore che dipende dalla equazione di partenza e dal valore di k. Possiamo ritrovare facilmente i nostri esempi: k = 2 con un solo valore finale; k = 2.7, analogo, anche se raggiunto con una oscillazione smorzata; k = 3.2 con una sola biforcazione; k = 3.5 con due biforcazioni; k = 3.7 caotica.

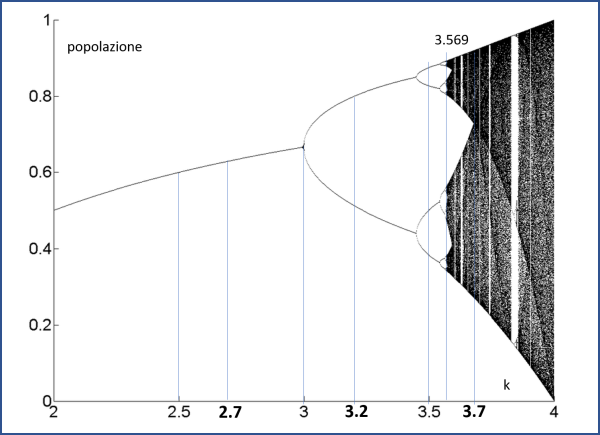
Dopo k = 3.569 sembra perdersi del tutto una qualche parvenza di periodicità. La popolazione è rappresentata da valori che non coincidono mai con un valore già ottenuto, come si può notare  dal fatto che i punti riempiono densamente uno o più intervalli. Infatti, nel diagramma di biforcazione, cominciano a comparire, lungo la verticale, delle zone nere (densamente riempite di punti).

Qualsiasi conclusione è ancora prematura, anche se sembra veramente assurdo che una equazione di secondo grado, chiaramente deterministica, riesca a produrre il caos. Da questi andamenti si intuisce l’origine del termine “caos deterministico”: sebbene i valori delle y siano ottenuti attraverso l'applicazione ripetuta della funzione relativamente semplice, cioè un meccanismo puramente deterministico, questi sembrano susseguirsi in modo "apparentemente casuale", senza alcuna regolarità o ricorrenza. Notiamo, inoltre, come nelle fasi antecedenti il caos si stia delineando una struttura frattale che poi sembra perdersi del tutto.

Torniamo alla farfalla

Abbiamo visto un modello molto semplice, ma già tale da mostrare una sensitività altissima alle condizioni di partenza. Proprio ciò che viene evidenziato dal modello più elaborato che porta all'effetto farfalla.

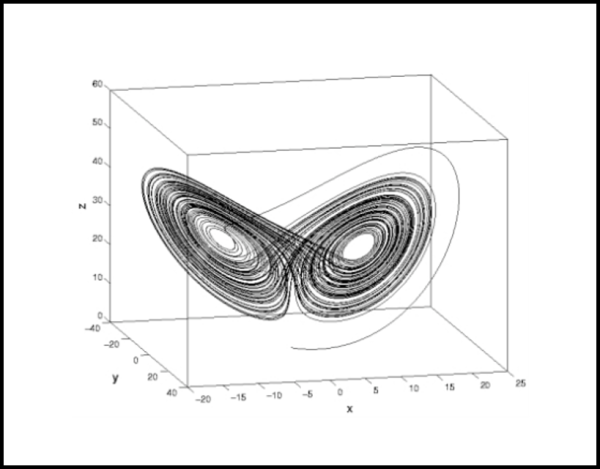
Quest'ultimo, però, dona qualche spunto in più sulla ancora scarsa conoscenza del fenomeno. In esso vediamo che i punti di una traiettoria, che per brevi intervalli temporali sembrano muoversi in modo sregolato, nel lungo periodo non si sparpagliano in modo casuale nello spazio degli stati ma vanno a disporsi su "nuvole" di punti che assumono determinate strutture geometriche "emergenti". Questo è proprio ciò che notò Edward Lorenz mentre stava studiando modelli dinamici utilizzati per le previsioni del tempo. Una volta constatata la sensitività rispetto alle condizioni iniziali, egli si accorse che rappresentando le traiettorie nello spazio tridimensionale delle variabili di stato queste andavano a disporsi su una particolare figura che non mutava cambiando le condizioni iniziali. Si trattava di un attrattore caotico, che venne poi chiamato “attrattore strano di Lorenz” . La sua forma a farfalla (Fig. 15) ci dà informazioni utili perché ci dice che, per quanto bizzarre, le traiettorie rimangono intrappolate all'interno di quella figura. Inoltre la forma e l'estensione dell'attrattore dipendono dai parametri, e da questo si possono dedurre, ad esempio, informazioni sull’ampiezza delle oscillazioni climatiche, pur non permettendo di fare previsioni a lungo termine circa le condizioni meteorologiche.

La scoperta del caos deterministico dimostra che modelli matematici non lineari e deterministici possono generare andamenti imprevedibili ed estremamente sensibili a piccole (anche impercettibili) perturbazioni. Da un lato, questo fatto diminuisce la capacità di fare previsioni mediante modelli matematici quando questi sono non lineari; dall'altro, però, suggerisce che fenomeni del mondo reale che ci appaiono del tutto aleatori, quindi non adatti a essere rappresentati mediante modelli matematici deterministici, potrebbero in realtà essere governati da equazioni ben precise, sebbene non lineari.

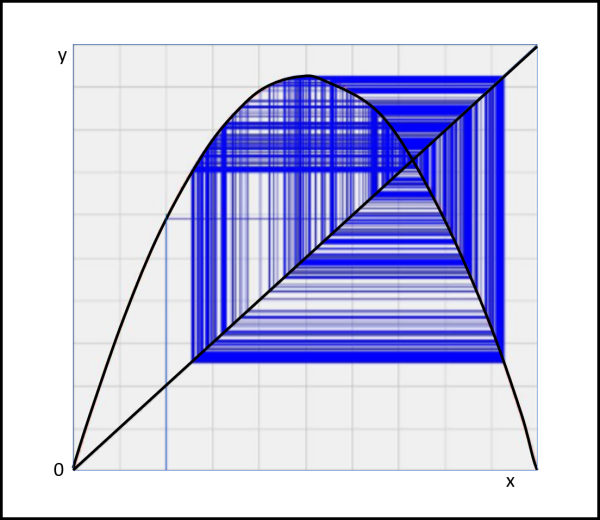
Non dimentichiamo, poi, nemmeno il fatto che l’esempio dell’evoluzione degli insetti proposto precedentemente faccia pensare a una figura frattale, come sembrano dimostrare le continue biforcazioni. E’ vero anche il viceversa, però… una evoluzione del tutto casuale (apparentemente caotica) possa creare una figura tra le più conosciute dei frattali (il triangolo di Sierpinski). Il filmato che segue mostra il procedimento da usare e il risultato sembra veramente impressionante.

Siamo appena all’inizio della comprensione del caos e di quello deterministico in particolare… chissà se il cervello dell’uomo sarà ancora in grado di risolvere il caos o sarà distrutto proprio da lui? Al momento, almeno, propendo per la seconda soluzione. Un esempio? Beh… si cerca di imporre un sistema dinamico semplificato per le previsioni climatologiche e ci si vuole convincere che la soluzione non sia assolutamente legata alla precisione e alla completezza dei dati di ingresso e nemmeno alle infinite variabili ancora nascoste. Insomma, una negazione assoluta della dinamica caotica, ampiamente dimostrata dalla Scienza.

Per finire in bellezza ecco un bel video su un altro sistema deterministico, ma altamente caotico: il pendolo doppio. Buon divertimento!