Le recondite armonie delle risonanze **
Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.
Sarà perché è Natale o perché la meccanica celeste mi ha sempre affascinato, fatto sta che vorrei parlare del misterioso mondo delle risonanze orbitali. Esse sono figlie di una madre potente e illimitata: la forza di gravità. Eppure, riescono a lanciare segnali e informazioni, a cambiare drasticamente la Natura, attraverso silenziose azioni apparentemente trascurabili. Se la gravità è un suono assordante e immutabile, le risonanze sono una musica di sottofondo, una ricerca di equilibri e sfaccettature, degna di un grande compositore. Facciamo silenzio e cerchiamo di udire queste “recondite armonie”, anche se la loro spiegazione accurata va oltre i limiti di questo nostro gruppo di amici. Comunque, non abbiate timore, ce n’è abbastanza per rimanere ammaliati e ammirati sia della Natura che di coloro che sono riusciti a esprimerle in termini matematici. L’articolo è decisamente lungo, anche se l’argomento è stato solo sfiorato. Sbocconcellatelo lentamente durante le Feste…
Un po’ di filosofia gravitazionale e/o di gravità filosofica
La gravità domina l’Universo. E quando non lo domina riesce a far sì che la sua espansione non sia incontrollata e distruttiva (forse per sempre). Non ha limiti di spazio e le sue braccia senza fine arrivano ovunque, anche se in condizioni debolissime e critiche. Potremmo tranquillamente dire che “matematicamente” la gravità della galassia più lontana si fa sentire in qualche modo anche sulla Terra. Non sappiamo dove sia oggi, ma sicuramente un filo impercettibile ci lega a lei come a tutto ciò che esiste nell’Universo. Einstein ha anche eliminato il fattore tempo, quello che limita le informazioni che sono costrette a viaggiare alla velocità della luce. La gravità non ha bisogno di messaggeri, ma agisce sul tutto e nello stesso momento: essa deforma lo spazio e il tempo e le sue pieghe più recondite spostano, deviano, modificano, all’unisono. Essa crea la scena in sui si muovono i personaggi: se vi è un buco o anche una piccola fessura nel “terreno” chiunque passa di lì lo subisce, a qualsiasi distanza sia da colui che ha creato la deformazione. E’ la teoria della relatività, signori e, se si accetta lei, si deve accettare questo ruolo straordinario della gravità.
Sembrerebbe che io faccia il tifo per Einstein e che voglia dimenticare le conquiste e le evidenze assurde ma reali della meccanica quantistica? No, il legame tra relatività e MQ deve esistere e deve essere più semplice di quanto si creda. Ci siamo forse stupiti dell’entanglement quantistico? In realtà sì, ma più che stupiti siamo stati scioccati da un fenomeno illogico. Poi è stato accettato, in attesa di una risposta “logica” definitiva. Perché allora non pensare che anche la gravità ci nasconda qualcosa di simile? Una caratteristica tale che l’informazione sia istantanea e senza limiti di spazio.
La migliore visione attuale è la deformazione spazio-temporale, una descrizione sicuramente magnifica e ben più raffinata di quella di Newton, ma -forse- solo un effetto di una causa ancora nascosta. Proprio pochi giorni fa abbiamo parlato degli strani effetti di entanglement tra particelle che simulano le azioni gravitazionali più complesse, accettate e descritte dalla relatività: i buchi del verme, i “wormhole”, quelle veloci scorciatoie, quelle gallerie che potrebbero legare qualsiasi luogo in qualsiasi istante, anzi senza nemmeno dover sottostare alle regole dello spazio e del tempo.
I buchi neri sarebbero le monumentali entrate a livello macroscopico, ma chissà quante entrate e uscite vi sono sotto i nostri occhi scendendo a livello particellare. Perfino la necessità di nuove dimensioni, per costruire questa ragnatela fitta e indistruttibile, spaventa sempre meno.
Eppure, giunti a questi livelli di pensiero, non dobbiamo assolutamente trascurare il grande Newton e tutta la scuola dei grandi meccanici celesti. Anzi le loro teorie, spiegazioni, soluzioni, sono servite e serviranno ancora di più nel futuro. Proprio i loro calcoli fantastici saranno il banco di prova delle più illogiche e affascinanti teorie. Vorrei ricordare un pensiero di Laplace, uno dei massimi studiosi del problema degli n-corpi, che vale più di tante mie parole…
“Dobbiamo, dunque, considerare lo stato presente dell'universo come effetto del suo stato anteriore e come causa del suo stato futuro. Un'intelligenza che, per un dato istante, conoscesse tutte le forze da cui la natura è animata e la situazione rispettiva degli esseri che la compongono, se fosse abbastanza vasta da sottoporre questi dati ad analisi abbraccerebbe nella stessa formula i moti dei corpi più grandi dell'universo e quelli dell'atomo più leggero: per essa non ci sarebbe nulla d'incerto, ed il futuro come il passato sarebbe presente ai suoi occhi” (1812).
Una frase profonda, oltre l’apparenza. Ovviamente si basa su un determinismo spinto, lo stesso che Einstein non ha mai voluto abbandonare. Tuttavia, la sua visione corale tra il macro e il microcosmo anticipa in qualche modo le ricerche più moderne e sembra portare il rapporto causa-effetto fino alle apparenti illogicità della meccanica quantistica.
Perché tante parole? Perché la meccanica celeste non ha perso un filo del suo valore e della sua importanza. Al limite, può essere integrata dai risvolti relativistici (come per la precessione del perielio di Mercurio), ma non viene mai alterata o svilita. Essa rimane la migliore descrizione di ciò che il suono assordante della gravità può causare all’interno di un sistema planetario (ma non solo) e solo lei riesce a cogliere, in questo monotono frastuono, le sottili armonie delle risonanze. Una musica dolce e mai aggressiva che però può portare a situazioni che stravolgono la loro stessa madre: la gravità.
Il problema dei due corpi e l’importanza della matematica
Il moto di due corpi attorno al proprio baricentro deriva direttamente dalla legge di Newton. Una legge del moto permette quasi sempre di scrivere un’equazione “differenziale” , che caratterizza il movimento di un corpo attraverso velocità e accelerazione (ecco perché le derivate diventano fondamentali). La soluzione di questa equazione permette di descrivere istante per istante il movimento futuro (e anche passato). Per la soluzione entrano in scena gli integrali.
Capite, adesso, l’importanza fondamentale della matematica nella fisica? Le derivate ci danno le informazioni concise e sintetiche del fenomeno o del meccanismo, regolato da una precisa legge fisica; gli integrali ci permettono di dedurre ciò che succede nel tempo. Il problema dei due corpi può essere espresso molto bene da equazioni differenziali che esprimono velocità e accelerazione.
Entrambe sono essenziali per sintetizzare il tipo di movimento nella sua completezza. Non basta sapere come un oggetto vari lo spazio percorso nel tempo (velocità), ma anche come possa o non possa variare la sua velocità (accelerazione). Abbiamo già imparato a vedere come una funzione (la retta) indichi perfettamente il modo sintetico per rappresentare la velocità in un moto semplicissimo, quello rettilineo uniforme (vedete come niente della geometria e della matematica è fine a se stesso!). Per moti più complicati le equazioni si complicano, ma, se i corpi in gioco sono solo due, le equazioni sono “integrabili”, ossia è possibile risolverle attraverso un processo matematico perfettamente applicabile.
In fondo è un grande gioco: prima si deve sintetizzare e mettere nella giusta forma il problema da risolvere e poi, se abbiamo agito bene, basta risolverlo. Se volete fare un trasloco che sia rapido, efficiente e controllabile, dovete prima preparare varie casse, separando gli oggetti e predisponendo il tutto per l’arrivo del camion. Poi, per lui sarà facile arrivare nella nuova destinazione. Immaginate, invece, se non preparaste niente e inseriste nel cassone dell’automezzo i singoli oggetti casalinghi uno a uno: un libro, un martello, un frullatore, una pentola, un altro libro, ecc., ecc. Non penso proprio che il camion aspetti la vostra pantomima e se ne andrà mandandovi anche al diavolo. Nemmeno ci penserà a risolvere l’integrale.
Tuttavia, non sempre le casse possono essere preparate in modo efficiente e trasportabile. Magari, avete uno scheletro di balena in soffitta e/o abitate su una collina raggiungibile solo a piedi: il camioncino che vi hanno mandato non può assolutamente risolvere i vostri problemi di trasloco!
Un terzo incomodo e tutto va all’aria
Nel sistema solare, la situazione è sempre quest’ultima. Basta che ai due corpi, Terra e Sole, ad esempio, si aggiunga un terzo corpo, Giove (ma anche molto meno), ed ecco che non è possibile risolvere l’equazione differenziale che abbiamo predisposto con tanta cura. E’ il tipico problema dei tre corpi, analiticamente irrisolvibile e quando dico irrisolvibile dico proprio irrisolvibile, dato che lo hanno affrontato i più grandi meccanici celesti degli ultimi secoli.
Qualcuno è riuscito a trovare delle soluzioni particolari (un po’ come quando una funzione matematica degenera… lo vedremo tra non molto) come il grande Lagrange con i suoi celebri punti L1, L2, L3, L4 e L5, tanto importanti sia nel sistema solare sia nei sistemi binari stellari per determinare i lobi di Roche e il “trasloco” di materia da una stella all’altra.
Tuttavia, il problema generale rimane insolubile. Figuratevi, poi, se volessimo tenere in conto tutti gli altri pianeti, asteroidi, comete, la stessa polvere interplanetaria. Il problema diventerebbe degli n-corpi e la situazione veramente tragica, senza nemmeno inserire altre variabili, come la non costanza del Sole, il passaggio di stelle vicine, le forze galattiche e… via dicendo.
Siamo di fronte a un problema che è essenzialmente deterministico, ossia si sa a quali legge deve obbedire, ma che è impossibile risolvere. L’unica possibilità, oltre che eseguire approssimazioni più o meno importanti, è quello di integrare, ossia affrontare la questione, numericamente. In poche parole, risolvere il problema per un intervallo di tempo relativamente breve, come se fosse dei due corpi, congelando tutte le posizioni degli altri, ma tenendo conto dei loro effetti. Poi, cambiare la posizione di tutti i corpi del Sistema Solare, bloccare nuovamente la situazione e risolvere il moto di due corpi, e via dicendo. Un passetto dietro l’altro, modificando, quando necessario, l’intervallo di tempo su cui si possono fare le approssimazioni. Nel frattempo, controllare costantemente gli errori commessi affinché essi siano sempre più piccoli di un certo valore scelto a priori.
L’ho fatta semplice, ma anche i più grandi calcolatori quasi impazziscono per tenere sotto controllo tutte le variabili. Ricordo, nel mio piccolo, che per integrare alcune decine di NEA su tempi di pochi milioni di anni abbiamo dovuto “far girare” il computer per alcuni mesi, senza mai fermarlo.
Normalmente, si scelgono approssimazioni diverse per il tipo di risultato che si vuole. Non sempre, però, le cose funzionano bene anche con questi palliativi informatici. Pur utilizzando le stesse condizioni di partenza, i risultati sono sempre diversi. Com’è possibile? Forse il determinismo è andato a frasi friggere? No, non è proprio così. La situazione resta, comunque, deterministica, ma una variazione impercettibile nelle condizioni di partenza (a volte solo il tipo di calcolatore usato, ma anche meno) porta in breve a risultati completamente discordanti.
Mamma… che caos!
In poche parole, le condizioni sono deterministiche, ma l’effetto di una certa causa è imprevedibile. Cadiamo nel caos, il caos matematico, che ha tutta una sua storia alle spalle che spaventerebbe qualsiasi matematico di medio livello. Fortunatamente, il caos a volte è facile da determinare. Mi spiego meglio: è facile rendersi conto che siamo in condizioni caotiche. Basta un esponente di una certa equazione esponenziale (capite già adesso perché dovremo studiare anche queste funzioni e un numero famoso e misterioso come il numero e ?) per dirci se il sistema è caotico oppure no. Il suo nome è affascinante: esponente di Lyapunov. Ed è anche semplice da capire. Esso misura quanto velocemente due traiettorie, entrambe plausibili per certe condizioni iniziali prestabilite, si allontanino l’una dall’altra. Più velocemente lo fanno e più il caos è “cattivo”. Pensate che attorno ai punti lagrangiani instabili esiste solo il caos e niente è più prevedibile.
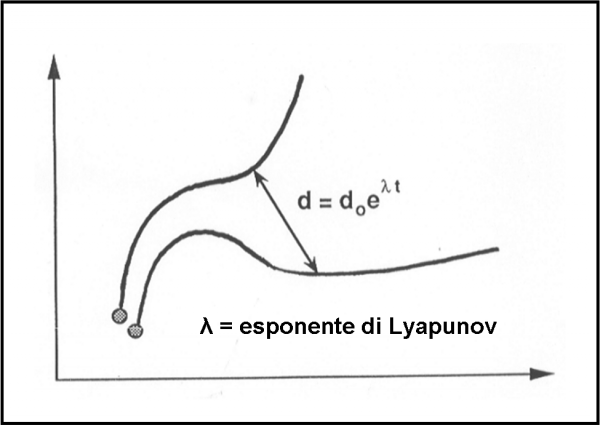
Fatemi porre una domanda che sembra tipica dei romanzi di fantascienza e che invece ha un senso matematico e fisico: “I pianeti rimarranno vicini alle loro orbite attuali oppure gli effetti cumulativi di piccole perturbazioni cambieranno le orbite su tempi lunghi, fino a farli collidere con il Sole o ad essere espulsi dal sistema solare?”. Ebbene, nessuno può realmente rispondere e se può tentare una risposta deve limitarsi a tempi scala ben inferiori a quelli del futuro del Sistema Solare. A volte non più di cento milioni di anni. Ci torneremo sopra.
Il caos è un problema mostruoso e il clima terrestre ne è un esempio perfetto. Capite perché mi arrabbio tanto con chi pretende di avere predisposto un modello matematico sicuro per la previsione delle variazioni climatiche? E’ un assurdità per definizione. Chi lo dice non è un vero scienziato o vuole prenderci in giro: non esiste altra soluzione!
Non voglio ripetere l’ormai risaputo esempio della farfalla che batte le ali sull’Himalaya e domani farà piovere a Milano. Preferisco tradurre una riflessione della maestosa mente di Poincaré, uno dei maestri più grandi della meccanica celeste. Ancora oggi le sue equazioni e le sue soluzioni particolari sono alla base dei calcoli più raffinati. Qualsiasi cosa pensiate di fare in meccanica celeste, Poincaré l’aveva già pensato e sviluppato.
Egli diceva: “La casualità più grande della Natura è la nascita di un grande uomo. E solo per un caso che si sono incontrate due cellule genitali di sesso differente che contengono precisamente, ciascuna per proprio conto, gli elementi misteriosi attraverso cui le reazioni mutue possono produrre un genio. Sarete tutti d’accordo che questi elementi devono essere molto rari e il loro incontro ancora più raro. La più piccola deviazione dello spermatozoo che trasporta un certo tipo di informazione può cambiare drasticamente il risultato. Un decimo di millimetro di spostamento e Napoleone non sarebbe nato e il destino di un intero continente sarebbe stato diverso” (1908).
Se da un lato il pensiero di Poincaré può far sorridere nel vedere quanta ammirazione era ancora posta in Napoleone, i concetti che esprime sono quanto di meglio si poteva concepire all’inizio del secolo scorso. Ricordiamo che l’effetto farfalla della climatologia nasce solo negli anni ’60.
Mentre la fisica dell’Universo faceva passi da giganti ed era al centro dell’attenzione, esistevano studi matematici che raggiungevano vette altissime e che avrebbero permesso di comprendere in qualche modo la struttura dinamica del sistema Solare. Senza di loro i viaggi interplanetari sarebbero ancora un’utopia.
Sto perdendo tempo, ma ci tenevo a collocare le ricerche di meccanica celeste in un contesto più generale possibile, anche perché non potremo certamente entrare nelle loro espressioni matematiche, veramente allucinanti per i non addetti ai lavori.
Anche se basate su equazioni legate alla fisica newtoniana, sono perfettamente applicabili alla visione einsteniana e forse possono andare anche oltre. Nei confini del sistema solare la meccanica celeste descrive qualsiasi piccola ruga del tessuto spazio-temporale descritto dalla relatività di Einstein. Non solo, quindi, il suono dirompente del buco gravitazionale di un unico corpo dominante, ma anche tutte quelle sottili variazioni di armonia nascosta che possono causare vie alternative, a volte impercettibili e a volte drammatiche e irreversibili.
Entriamo, quindi, finalmente, nel mondo silenzioso e imprevedibile delle risonanze orbitali, frutto misterioso e nascosto delle perturbazioni gravitazionali tra un numero impressionante di corpi interagenti. Un suono, un’informazione che assomiglia al canto delle balene. Un ordine, un comando, un suggerimento che si trasmettono a distanze non del tutto trascurabili nemmeno per la luce, ma che le risonanze sono, invece, in grado di applicare a una rete immensa, intricata e sempre perfettamente controllata. Anche quando sembra portare al caos più drammatico. Non sembra, forse, una specie di “entanglement”…?
Disturbi occasionali e periodici
Abbiamo visto come il moto regolare di un oggetto attorno a un altro (più esattamente di entrambi attorno al baricentro del sistema) sia solo un’astrazione matematica, irrealizzabile in Natura. Le leggi di Keplero sono teoriche e nessun oggetto è in grado di seguirle esattamente. In parole ancora più comprensibili: nessuno oggetto del Sistema Solare ritorna esattamente al punto di partenza dopo aver completato un angolo di 360°. Ogni pianeta, grande o piccolo che sia, disturba l’esecuzione del balletto orbitale. Spintarelle, piccoli scossoni, attrazioni, e chi più ne ha più ne metta, non permettono la soluzione dell’equazione del moto.
A volte esse sono del tutto casuali e irrepetibili. Pensate a una cometa che si avvicina al Sole: la sua vita potrebbe dipendere da quanto passa vicino a un gigante come Nettuno o Urano o Saturno, per non dire Giove. Una perturbazione “unica” ma decisiva, in grado di mutare completamente il futuro della piccola vagabonda. Quante volte la nostra Terra ha rivoluzionato il futuro di rocce vaganti nello spazio? Un numero incredibile di volte, certamente. Noi abbiamo una costante paura dell’impatto di un asteroide contro di noi e studiamo con attenzione ogni passaggio ravvicinato, che avviene giornalmente o annualmente o secolarmente, a seconda delle dimensioni, ma non parliamo mai dei danni che il nostro pianeta ha causato e continua a causare al piccolo visitatore.
La sua orbita è stravolta e il suo futuro cambiato per sempre. Magari era riuscito a trovarsi una posizione abbastanza tranquilla e duratura ed ecco che il nostro pianeta, senza curarsi di lui, lo caccia dal Sistema Solare o lo fa finire direttamente nella fornace stellare. Questi sono fenomeni del tutto casuali, a volte prevedibili, a volte assolutamente no. Gli effetti possono essere gravissimi, ma la loro importanza è -in qualche modo- secondaria.
Quando ero militare mi si diceva: “In guerra importano molto di più le ustioni di secondo grado che non quelle di terzo. Queste ultime, distruggono le cellule e non vi è necessità di curare e di perdere tempo. Quelle di secondo, invece, devono essere curate per cercare di rimandare il soldato in prima linea”. Un discorso cinico ed eticamente assurdo, ma che ha una sua logica spietata: meglio causare feriti che morti. Le bombe che esplodono lanciando frammenti invisibili ai raggi X danno problemi ben maggiori di quelle che amputano un arto o causano la morte. Che schifo… torniamo a noi.
Il discorso “bellico” calza, però, a fagiolo. Sono molto più subdole, sottili e misteriose le perturbazioni che non si limitano a colpi duri ed evidenti, ma quelle che agiscono su tempi lunghi, ripetendo configurazioni che prima o poi conducono verso il disastro (o alla salvezza). Loro vanno studiate ed analizzate e non solo accettate come un evento fortuito.
E’ un po’ come la legge del “fil ferretto”: a furia di piegare un filo di ferro, esso alla fine si rompe. Le perturbazioni che si ripetono periodicamente, seguendo uno schema più o meno lungo e complicato, possono portare alla rottura di un filo che sembrava indistruttibile. Ed esse possono essere studiate matematicamente anche se a volte con difficoltà estrema. Ciò non vuol dire che portino a soluzioni uniche e controllabili. In molti casi si sa esprimere molto bene la causa, ma non si è in grado di descriverne gli effetti. In parole più tecniche: si esprime una legge che determina particolari condizioni ripetitive, ma queste non sono né risolvibili né prevedibili e portano al caos.
Noi siamo proprio interessati a questi eventi ripetitivi o -almeno- a quelli più noti e facilmente descrivibili. Essi prendono il nome generale di risonanze orbitali. Esse si propagano da un oggetto a un altro, a volte a breve distanza, a volte anche molto lontano. Vibrazioni, deviazioni, incontri che sembrano scanditi da un cronometro, piccoli segnali che la gravità manda in giro quasi sussurrando. Anche le più sottili e delicate tra loro hanno il tempo di ottenere qualche effetto. Basta aspettare… e il Sistema Solare ha sempre molto tempo a disposizione.
Prima di analizzarle in maggior dettaglio, richiamiamo ancora una volta il concetto relativistico di gravità. Le risonanze sono zone particolari che subiscono piccole deformazioni spazio-temporali proprio ogni volta che un certo oggetto le attraversa. Un piccolo marciapiede o una crepa nella strada. A furia di passarci sopra la sconnessione può allargarsi o il marciapiede può venire urtato portando a soluzioni imprevedibili. Si può tornare in carreggiata, si può scivolare e rialzarsi evitando la traiettoria così pericolosa, oppure si può precipita in un burrone. A volte questi passaggi ripetuti permettono di trovarsi un angolino particolare, al riparo dagli scossoni, ossia dalle pieghe e dalle deformazioni impreviste. Si può essere coraggiosi o timorosi; si può rischiare senza paura di emigrare o si può preferire, invece, rintanarsi al caldo in una rientranza semi nascosta ma sicura.
Uno scambio di informazioni quasi invisibile, che continua a permeare l’intero Sistema. Ognuno può dire la sua e prendere decisioni rivoluzionarie. E’ un’azione spesso corale in cui molti oggetti sono coinvolti. Sembra quasi che avvenga di nascosto alla forza principale, alla signora dei moti planetari. No, non illudiamoci. Anche se sembra disinteressarsi, è sempre comunque la gravità che comanda le variazioni sul tema, che permette alle recondite armonie di assumere momentaneamente un ruolo di primo piano. In una grande orchestra è necessario sia il violino che il triangolo, ma è sempre il direttore che controlla e guida il risultato finale.
A questo punto, possiamo trascurare la visione relativistica e lavorare tranquillamente con le leggi del moto e con le descrizioni tipiche della meccanica celeste. Sappiamo benissimo che le conclusioni sono perfettamente equivalenti.
Le risonanze orbitali
Come si può definire, in generale, una risonanza orbitale? Essa è una situazione che si ottiene quando il movimento di due corpi planetari attorno al Sole (o attorno al proprio pianeta) porta a configurazioni geometriche ripetitive, di tipo periodico, tra i due oggetti. Gli effetti sono importanti quando le configurazioni particolari si ripetono abbastanza frequentemente.
Cosa deve succedere affinché certe configurazioni si ripetano periodicamente e in tempi rapidi? Basta che i periodi orbitali dei due oggetti abbiano un rapporto uguale a quello di due numeri interi abbastanza piccoli, del tipo 2/1, 3/1, 3/2, 4/1, 5/2 e via dicendo… Abbiamo già visto varie volte come funziona un risonanza di questo tipo (ad esempio, sui due libri sull’Universo) ed è inutile ripeterla ancora.
E’, comunque, intuitivo pensare che se due oggetti stanno nella risonanza 3/1, ad esempio, vuol dire che mentre un corpo esegue una rivoluzione completa, l’altro ne esegue esattamente tre. Questa caratteristica delle orbite porta i due oggetti a trovarsi periodicamente (ogni tre periodi di uno e ogni periodo dell’altro) nella stessa identica configurazione geometrica di partenza. Stesse condizioni geometriche vogliono anche dire stessi effetti gravitazionali e quindi stesse perturbazioni. Il ripetersi della stessa configurazione può causare sia stabilità che instabilità e non è assolutamente facile prevedere quando avviene una o l’altra.
Facciamo l’esempio di un’altalena. Diamo un colpo deciso al bimbo che vuole dondolare. Se fossimo in condizioni perfette, l’oscillazione andrebbe avanti all’infinito. Purtroppo, ci sono gli attriti della corda, dell’aria, i movimenti del bambino, anche solo una farfalla che si posa sul ramo, e ogni tanto il papà deve dare un nuovo colpo all’altalena.
Attenzione, però. La spinta deve essere data al momento giusto, nel punto giusto e con la giusta forza, per far riprendere l’oscillazione e magari aumentarla. Se si sbaglia di poco, si rischia di bloccare l’altalena o di causare qualche effetto ancora più strano. Abbiamo un moto continuo (l’altalena che oscilla) a cui si somma un’azione esterna di tipo ripetitivo e periodico che crea un effetto cumulativo sul primo movimento e ne accentua o ne disturba l’esecuzione. In alcuni casi l’oscillazione dell’altalena (l’orbita) può essere drasticamente modificata e portare anche a una caduta (fuoriuscita dalla risonanza). In altri casi, invece, l’oscillazione è continuamente rafforzata e stabilizzata. Stiamo parlando delle risonanze orbitali più semplici quelle che dipendono solo dal moto degli oggetti e che vengono chiamate di moto medio, in quanto ciò che le causa è proprio il moto medio degli oggetti (ossia il loro periodo).
In fondo, a parte il movimento fondamentale (l’oscillazione continua o l’orbita attorno al Sole), si stabilisce una silenzioso colloquio tra padre e figlio, un aiuto continuo che vuole portare a un maggiore divertimento del piccolo. Tuttavia, mai prenderlo alla leggera: ci vuole attenzione, dedizione e precisione per non rischiare qualche spiacevole incidente! Nel Sistema Solare, però, qualsiasi soluzione fa parte della vita del Cosmo e non c’è mai una riuscita buona o una cattiva. Esiste solo una modificazione, accettata sempre come una conquista.
Cosa succede, in pratica, a un oggetto che si trovi in una risonanza “distruttiva” (destabilizzante) con un pianeta? Un po’ alla volta l’eccentricità cresce costringendo l’oggetto che percorre un’orbita sempre più allungata ad avere incontri ravvicinati con altri oggetti celesti fino a uscire dalla risonanza. Una risonanza “costruttiva” (stabilizzante), invece, corregge automaticamente eventuali piccole variazioni inserendo l’oggetto in un’orbita e in una configurazione robusta e inamovibile. E’ sempre un qualcosa di simile all’equilibrio stabile o instabile: la pallina sopra la scodella tende a cedere per qualsiasi piccolo spostamento; quella in fondo alla tazza, anche se allontanata, torna alla posizione di partenza. Si può prevedere ciò che capita all’interno di una risonanza? Assolutamente no, dato che è patria indiscussa del caos.
Quello che non cambia quasi per niente durante l’evoluzione di un’effetto destabilizzante è il semiasse maggiore. Esso resta praticamente costante fintanto che l’oggetto non viene estratto dalla risonanza. D’altra parte una risonanza di moto medio si mantiene, qualsiasi sia l’eccentricità o l’inclinazione orbitale. Ciò che conta è il periodo di rivoluzione ed esso dipende solamente dal semi asse maggiore (come dice la terza legge di Keplero). Se cambiasse il semiasse, cambierebbe il periodo e la risonanza sparirebbe.
Per potere verificare queste ipotesi essenzialmente teoriche e agenti su tempi troppo lunghi per la durata della scienza astronomica umana (almeno qualche milione d’anni) sarebbe necessario avere un campione enorme di oggetti virtuali e vedere come agiscono le risonanze sui loro tempi scala. Oggi potrebbe anche essere fatto con le integrazioni numeriche del moto dei tre corpi (approssimato ma già sufficiente) e i calcolatori elettronici, ma una volta non era possibile.
Fortunatamente, le ipotesi potevano essere viste su una popolazione “reale” che era lì davanti agli occhi di tutti: gli asteroidi. Per centinaia e centinaia di loro si conosceva l’orbita piuttosto bene e quindi era facile vedere cosa succedeva nelle zone in cui il semiasse portava a una qualche risonanza di moto medio con Giove. Come si può verificare facilmente l’effetto di una risonanza? Facilissimo: per vari valori del rapporto di risonanza (1/2, 2/3, 3/4 , ecc.) è possibile calcolare il relativo semiasse maggiore. Infatti il rapporto tra i periodi è proporzionale al rapporto tra i semiasse (sempre per la terza legge di Keplero). Impostando il rapporto e conoscendo il semiasse di Giove è immediato trovare il semiasse dell’orbita asteroidale che corrisponde a quella particolare risonanza.
La distribuzione degli asteroidi in funzione del semiasse maggiore identifica immediatamente le risonanze distruttive e quelle stabilizzanti. Le prima saranno quasi prive di oggetti, le altre mostreranno addensamenti. Vi prego di non chiedermi perché alcune risonanze sono “cattive” e altre “buone”. Ci sono tante teorie, ma ancora non vi è alcuna certezza. La stessa risonanza può essere distruttiva tra gli asteroidi e essere stabilizzante in altre situazioni. I giochi di pretigio non devono essere svelati completamente!
C’è chi scappa e chi fa acrobazie
Guardiamo attentamente il digramma che mostra la distribuzione asteroidale. Si vedono chiaramente delle lacune, svuotate dei loro antichi oggetti, in corrispondenza delle risonanze 3/1, 5/2, 7/3 e 2/1 (potete anche scriverle al contrario, ossia 1/3, 2/5: tutto dipende se mettete sopra l’asteroide o Giove). Calcoli numerici mostrano chiaramente che nel giro di pochi milioni di anni un oggetto inserito dentro una di queste risonanze viene espulso dal sistema solare (passaggio ravvicinato con lo stesso Giove) o costretto ad avere incontri con i pianeti interni, da Marte a Mercurio (Terra e Venere i più importanti, data la loro maggiore massa). In quest’ultimo modo si originano i NEA, che tanta paura incutono ai poveri terrestri, uomini o dinosauri che siano.
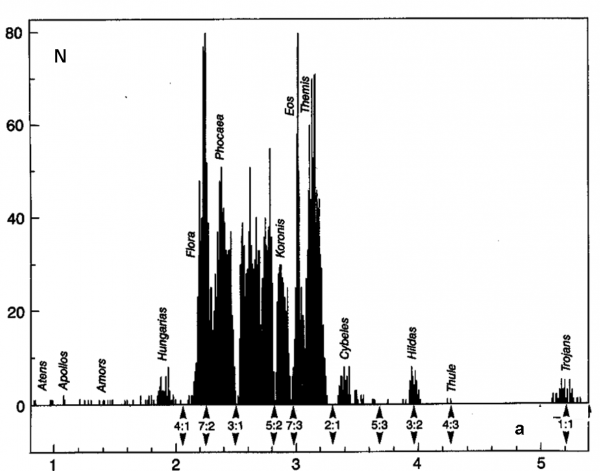
La maggior parte di essi, però, continua ad aumentare la propria eccentricità fino a finire direttamente tra le braccia del Sole. Oltre la risonanza 2/1 (molto potente), abbiamo invece la 3/2, la 4/3 e soprattutto la 1/1 che sono stabilizzanti. In quella posizione si notano gruppi più o meno numerosi di oggetti. I primi appartengono al gruppo di Hilda, i secondi all’oggetto Thule e qualche nuovo piccolo arrivato. L’ultima è la più famosa e ospita i troiani, ossia quelli che seguono o anticipano l’orbita di Giove, stando però proprio su di lei. Essi occupano i celeberrimi punti lagrangiani L4 e L5.
Gli oggetti che si sistemano in modo stabile all’interno di una risonanza di questo tipo, non possono però rivolvere a piacere. Possono sopravvivere solo se mantengono una distanza di sicurezza con Giove. A parità di periodo orbitale, si vedono ancora vivi e vegeti solo quelli che sono riusciti ad evitare incontri ravvicinati con il gigante gassoso. E’ interessante notare la posizione reale degli oggetti del gruppo di Hilda e dei troiani rispetto a Giove. Nelle due figure è stato “bloccato” Giove (i movimenti sono quindi relativi a lui) e si notano bene le figure secondo le quali si distribuiscono gli asteroidi che hanno capito la lezione di sopravvivenza.


Gli Hilda danno origine a una bellissima figura triangolare, il cui unico scopo è svuotare la zona troppo vicina al pericolo pubblico numero uno. I troiani, come ormai ben sapete, si distribuiscono davanti e dietro al signore e padrone, in modo da formare un triangolo equilatero con lui e il Sole. In realtà le orbite oscillano attorno a certi valori, ma qui il discorso si farebbe troppo lungo e complicato. Posso solo dirvi che le soluzioni di integrali particolari e di equazioni terribili da un punto di vista matematico, danno luogo a balletti e a soluzioni veramente affascinati che assumono forme strane come un ferro di cavallo o una vera e propria altalena. Insomma, un Luna Park planetario!
Vi assicuro che, dopo aver aspettato magari mesi per far “evolvere” una serie di oggetti, immessi in condizioni simili, ma non perfettamente uguali, era sempre un’emozione dare il via alla visione grafica delle variazioni orbitali in funzione del tempo. Danze lenti e cadenzate, piroette improvvise, salti e giravolte. Sembrava di vedere fiocchi di neve sempre uguali e sempre diversi! A volte, lo ammetto, facevamo il tifo per l’oggetto che mostrava l’evoluzione più scenografica. In quel momento si sentiva veramente la musica delle risonanze e la perfetta armonia di quei segnali così silenziosi e così potenti. Poi, si ritornava seri, si faceva un po’ di statistica e si stabiliva quale era l’evoluzione che aveva la maggiore probabilità di accadere. Si stilava una classifica e una scala di percentuali. In regime caotico si può solo parlare di “probabilità” e mai di certezza. Probabilità, una parola che abbiamo già sentito molte volte nella MQ… Mi permettete una constatazione azzardata? Un’orbita caotica è rappresentabile come migliaia di possibili evoluzioni, ma se ne determino una, tutte le altre non hanno più senso. Un paragone azzardato, ma che ci riporta sempre a … bomba.
Non solo asteroidi
Vediamo, ora, abbastanza velocemente, se il resto del Sistema Solare ci mostra altri casi di risonanze di moto medio. Le situazioni interessanti sono molte e tutte hanno un tocco personale. Ognuna di esse meriterebbe una descrizione dettagliata. Spesso, le risonanze di moto medio sono aiutate dai moti processionali delle orbite (la rotazione di tutta l’orbita su tempi scala piuttosto lunghi, decine o centinaia di migliaia di anni). Le equazioni si complicano e danno luogo a giochi di “tira e molla” dinamici quasi da acrobati da circo. In parole povere, pensate che per ritrovarsi esattamente nelle stesse configurazioni, a volte si deve sfruttare l’aiuto che deriva dal continuo spostamento di tutta l’orbita. Un gioco di prestigio che ai pianeti e ai satelliti riesce, sovente, in modo perfetto.
Le risonanze di moto medio si notano molto bene negli anelli di Saturno. Anzi, sono proprio loro a modellarli attraverso zone più dense o completamente vuote. In fondo, gli anelli rappresentano una piccola fascia di asteroidi che girano attorno a un pianeta. La celebre divisione di Cassini è dovuta alla risonanza destabilizzante 2/1 con Mimas (con qualche ulteriore complicazione). Quella di Encke e di Keeler sono invece svuotate dalla risonanza 1/1 (questa volta destabilizzante) con Pan e Daphnis. Il bordo esterno dell’anello A è delimitato dalla risonanza 7/6 con Janus.
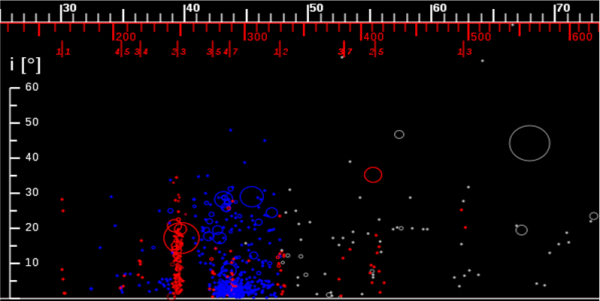
Anche nella zona trans nettuniana esistono molte risonanze di moto medio rispetto a Nettuno (il padrone del confine planetario), spesso stabilizzanti, come indica la figura che segue (notate Plutone e i suoi fratelli plutini, di cui parleremo tra poco), che rappresenta l’inclinazione dei TNO rispetto al semiasse maggiore (le risonanze costruttive danno luogo a linee verticali popolate di oggetti)
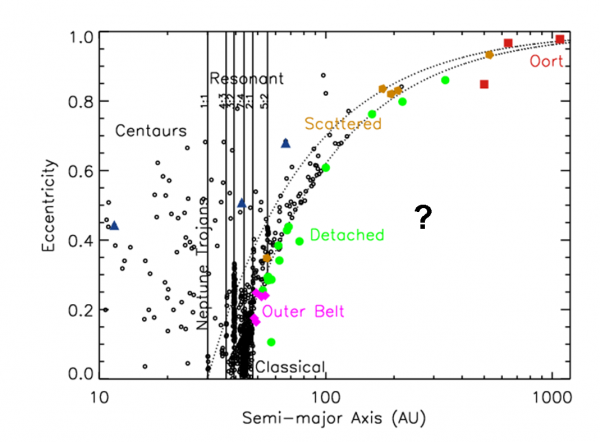
Ne riporto anche un’altra, analoga, ma in cui al posto dell’inclinazione si è rappresentata l’eccentricità. Anche se in modo meno evidente (vista la scala) si notano le stesse risonanze (d’altra parte chi le comanda è il semiasse). Che strana figura, però… Come mai sembra che gli oggetti si sistemino lungo una curva? Ho posto un punto interrogativo nel centro di una zona vuota. Ma è veramente vuota? Forza, datemi la risposta…
Finora, abbiamo soprattutto parlato di risonanze tra un piccolo oggetto e un pianeta decisamente più grande. Vi sono, però, molte risonanze stabilizzanti anche tra coppie di satelliti e/o pianeti e satelliti. Plutone ad esempio è in risonanza 2/3 con Nettuno e si può permettere perfino di attraversarne l’orbita (al momento giusto, però…). Una bella serie di risonanze si hanno nel sistema di Saturno. Tethys e Mimas stanno in risonanza 2/4 (no, non stupitevi se ho scritto 2/4 e non 1/2 che sembrerebbero la stessa cosa. La differenza sta nel fatto che in questo caso i satelliti devono aspettare un po’ di più per sfruttare un moto precessionale… robe da matti!). Dione ed Enceladus in quella 1/2, Iperione e Titano nella 3/4.
Ma sicuramente la più celebre è quella esistente tra i primi tre grandi satelliti di Giove (Io, Europa e Ganimede). Proprio questa risonanza accentua le configurazioni reciproche che aiutano nel riscaldamento mareale di Io e di Europa. Essa è una risonanza di moto medio, ma coinvolge in modo meraviglioso ben tre oggetti: i loro periodi attorno a Giove stanno nel doppio rapporto 1/2/4. Nel tempo che Ganimede compie una rivoluzione, Europa ne compie due e Io quattro. Un balletto perfetto e continuo, illustrato da filmato che segue.
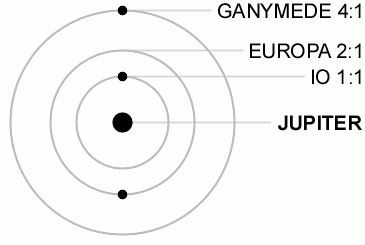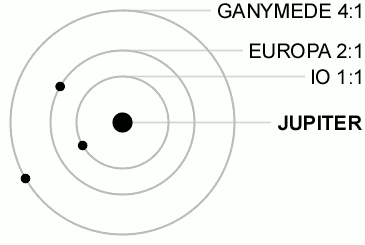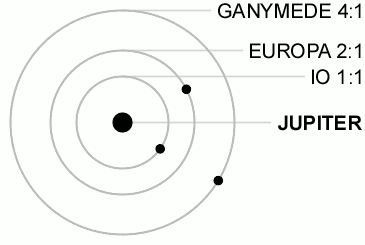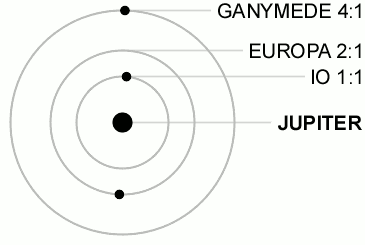
Quest’ultima risonanza, coinvolgendo tre oggetti, prende anche il nome di risonanza di Laplace ed è copiata pari pari in un sistema extrasolare, quello dei pianeti Gliese376 e,b,c. Quando gli riesce un bel gioco, l’Universo lo ripete!
Altre armonie più sottili
Se quelle di moto medio sono le più evidenti e semplici da spiegare, non sono però le sole risonanze. Se diamo tempo al tempo altre combinazioni possono essere altrettanto importanti. Non possiamo descriverle tutte (una, abbastanza anomala, l’abbiamo già trattata QUI, quella di Kozai; un’altra è molto complicata (di Lindblad) e causa le onde di densità che si notano negli anelli di Saturno, ma anche nelle spirali galattiche) e ne citiamo solo un tipo, veramente importante, anche se sembra quasi impossibile credere alla sua efficacia.
Sto parlando delle risonanze secolari, che sfruttano configurazioni ricorrenti tra periodi ben più lunghi di quelli di rivoluzione. Già sappiamo che esistono moti di precessione orbitale, ossia: nessuna orbita è fissa nello spazio. Quando ruota tutto il piano orbitale abbiamo una precessione della linea dei nodi (simile a quella che causa la ben nota precessione degli equinozi sulla Terra); quando, invece, vi è la rotazione dell’intera orbita sul suo piano orbitale, abbiamo la precessione del perielio ed è celebre quella molto evidente di Mercurio, anche per gli effetti relativistici che gli sono stati applicati.
Si ha una risonanza più o meno destabilizzante quando i periodi di precessione di due oggetti sono uguali. Su tempi abbastanza lunghi, milioni di anni, questa configurazione quasi impercettibile cambia sensibilmente le eccentricità e le inclinazioni delle orbite. Gli asteroidi subiscono pesantemente quella legata al periodo di precessione del perielio di Saturno. Nel diagramma semiasse maggiore - inclinazione degli asteroidi il limite superiore della distribuzione è proprio dovuto a questa risonanza secolare.
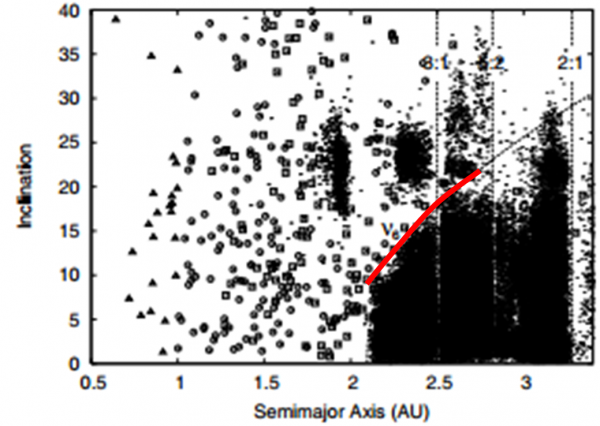
Non solo, però (e la cosa mi tocca molto da vicino…): le risonanze secolari con Saturno degli oggetti con orbite relativamente interne aumentano leggermente la loro eccentricità fino a riuscire ad attraversare l’orbita di Marte e avere incontri ravvicinati con il piccolo pianeta rosso.
Si pensava che l’influenza del mini-pianeta fosse secondaria e trascurabile. Insieme a un carissimo (e bravissimo) collega molto giovane (mancato tragicamente in un incidente di montagna, evento che mi ha tolto molta energia lavorativa negli anni precedenti la pensione) ci siamo detti: “Ma ne siamo proprio sicuri?”. Abbiamo preparato una bella lista di Mars-crossers e poi li abbiamo lanciati nella loro evoluzione dinamica per tempi scala di almeno un centinaio di milioni di anni.
C’era da aspettare parecchi mesi prima che il programma finisse i suoi calcoli ed era un po’ duro attendere “freddamente” il risultato (eravamo pur sempre dei “calorosi” italiani, molto impazienti). E così avevamo impostato una specie di segnale che ci avrebbe avvertito quando (e se) un asteroide avesse avuto un passaggio ravvicinato con Marte, ma soprattutto se avesse iniziato a decadere verso un’orbita ben più interna fino a diventare un NEA. In tal caso, avremmo trovato un nuovo serbatoio di oggetti a rischio di impatto, dato che quelli “normali” sembravano non mantenere da soli la popolazione attuale.
Sono dovute passare molte decine di milioni di anni (molte settimane reali) prima di avere il primo segnale. Poi altri e in numero crescente. Sì, avevamo avuto ragione: se gli si dà il tempo giusto i Mars-crossers diventano una sorgente importante di NEA. La risonanza con Saturno lavora molto bene e altrettanto bene anche la gravità del piccolo pianeta dinamicamente sempre snobbato.
Questi oggetti, che prima o poi verranno a trovarci, sono normalmente piccoli, inferiori ai pochi chilometri. Ma uno no. E ci divertimmo un sacco a prospettare un evento veramente catastrofico. In mezzo a tanti bambini vi era anche 313 Chaldaea, un gigante di circa 100 km di diametro. La sua probabilità di entrare e gettare sconquasso tra i pianeti interni non è nulla. Vi immaginate cosa rappresenterebbe un impatto contro un “meteorite” di100 km? Meglio non pensarci e sperare che Chaldaea segua una vita meno spericolata. Scusate la digressione personale, ma certi ricordi (anche se finiti tragicamente) non si possono dimenticare Voi mi capite sicuramente…
Torniamo alle risonanze secolari. Una piccola precisazione che forse avete già intuito. Le risonanze, pur essendo guidate dalla legge di gravitazione universale, dipendono, alla fine, ben poco dalle masse degli oggetti coinvolti. Se si cade in una risonanza si può essere grandi o piccoli, ma la sorte è la stessa. Ne segue che esse possono coinvolgere anche coppie di giganti.
Non posso entrare nei dettagli, ma sembra quasi sicuro che il valore dell’inclinazione di Saturno sia stata ottenuta attraverso una risonanza secolare tra il moto di precessione dell’asse di rotazione di Saturno e quello dell’asse del piano orbitale di Nettuno (ricordiamoci infatti che esistono anche le risonanze spin-orbita, di cui abbiamo già parlato QUI e che coinvolgono periodi di rivoluzione e di rotazione).
Le risonanze, però, spesso, vanno e vengono, magari solo a causa di una diminuzione di massa nella zona trans nettuniana. Eh sì, la farfalla che sbatte le ali può anche essere un numero maggiore o minore di corpi cometari. Le sfumature musicali delle risonanze arrivano a livelli appena percettibili, ma sono comunque essenziali.
Un futuro incerto
Si può, però, anche volare oltre. Come alcune risonanze spariscono nel tempo, altre possono nascere. Ad esempio, si ipotizza una futura risonanza secolare legata alla precessione del perielio di Mercurio e di Giove. Essa aumenterebbe di molto l’eccentricità del primo pianeta e potrebbe (dico “potrebbe”) destabilizzare l’intero Sistema Solare interno!
Questa visione semi-fantascientifica ci riporta a due considerazioni estremamente importanti. Se le risonanze vanno e vengono, è facilmente intuibile perché certi satelliti dei pianeti esterni mostrino episodi geologici dovuti a un forte riscaldamento interno. Essi sono avvenuti in periodi di tempo in cui erano attive risonanze molto “stressanti” per gli effetti mareali, che oggi sono ormai scomparse (Tritone potrebbe essere tra questi candidati, ma ce ne sono molti altri). Come già detto, basta ben poco (un battito d’ali) per cambiare le condizioni al contorno e innescare o distruggere una risonanza. In un’orchestra perfetta, basta un violino stonato per causare una catastrofe.
Più scioccante la seconda constatazione che ci ha già portato all’inizio dell’articolo a una domanda, ancora lasciata senza risposta: “I pianeti rimarranno vicini alle loro orbite attuali oppure gli effetti cumulativi di piccole perturbazioni cambieranno le orbite su tempi lunghi, fino a farli collidere con il Sole o a essere espulsi dal Sistema Solare?”
Se noi ci mettessimo a giocare con i periodi orbitali dei pianeti maggiori e con un po’ di rapporti tra numeri interi, anche non troppo piccoli, ci accorgeremmo che spesso e volentieri il rapporto tra i periodi è estremamente simile a un qualche rapporto numerico. Tanto per fare un esempio, la Terra e Venere sono vicinissime alla risonanza 8/13. Ancora peggio, Giove e Saturno non si discostano molto dalla 5/2. E che dire di Urano e Saturno con la 7/20 o di Urano e Nettuno con la semplicissima 2/1?
Beh… non spaventiamoci troppo. Questo è un gioco abbastanza “stupido”. Normalmente sono casi fortuiti e momentanei, nel senso che se oggi sembrano in risonanza, tra pochi decenni o centinaia di anni la combinazione numerica “salta” del tutto. Insomma, sono solo e soltanto delle coincidenze casuali che non possono lasciare alcun segno. Non sono armonie e nemmeno stonature, sono solo rumori apparenti e ininfluenti.
Sì, va bene… ma veramente tutte? Tra tanti “al lupo, al lupo” potrebbe anche scapparci quella buona. Magari, una risonanza non esatta potrebbe significare una vecchia risonanza che si sta “sciogliendo” sempre più, ma potrebbe anche essere il contrario. Certo non su scale di tempo facilmente verificabili, ma su decine e decine di milioni di anni se non su miliardi di anni.
In altre parole rieccoci alla domanda di prima: “Il sistema solare è stabile o subirà cambiamenti drastici e catastrofici in un futuro non certo prossimo, ma nemmeno tanto lontano?”. Come dicevo, la risposta è non solo difficile, ma praticamente impossibile. L’innesco di un futura risonanza non è prevedibile né, tantomeno, lo è il regime caotico a cui essa potrebbe dare il via. Non essere prevedibile, però, non vuol dire improbabile!
Poincarè diceva: “ Le condizioni iniziali sono sempre note con una certa approssimazione e quindi il futuro è noto con la stessa approssimazione”. Quanta saggezza e quanta verità in queste parole. Rifletteteci e capirete ancora meglio perché mi sono ostinato a parlare tanto di limiti e di differenze tra punto matematico e punto fisico. Il Sistema Solare è un sistema fisico e mai potrà essere descritto con parametri definiti da un infinito numero di cifre decimali. Il caos non aspetta altro!
I mezzi più sofisticati utilizzati oggi per simulare il futuro dei corpi planetari portano a risultati più o meno preoccupanti. Il problema dei tre corpi (una netta approssimazione che però può funzionare molto bene per casi locali) è perfettamente sotto controllo e può portare a valutare la stabilità di un sistema, senza errori significativi, anche su tempi scala lunghissimi.
Le cose cambiano andando verso situazioni più generali. Il sistema dei pianeti maggiori è stato calcolato numericamente fino a circa un miliardo di anni nel futuro. Alcuni risultati che se ne derivano sono piuttosto sicuri: Plutone ha un’orbita caotica: il suo destino è segnato e prima o poi lascerà l’attuale posizione. Meno male che non è più un pianeta… sai che figura avere un pianeta che ci dice addio e se ne va chissà dove!
Risulta, però, cambiando le condizioni iniziali nell’ambito delle approssimazioni oggi possibili, che i giganti possono risultare sia regolari che caotici. Hai detto niente!
Il grande J. Laskar, che ho avuto la fortuna di avere come amico, riuscì a simulare, con una tecnica sintetica sofisticatissima, il comportamento di tutti i pianeti per tempi di 10-15 miliardi di anni. Più che sufficienti pensando alla vita del Sole. Ebbene, i suoi risultati sono i seguenti: Giove, Saturno, Nettuno e Urano “sembrano” perfettamente regolari (beati loro!). Venere e Terra risultano invece “moderatamente” caotici. Quel “moderatamente” non è proprio un risultato ottimistico. Molto peggio va per Mercurio e Marte: essi sono “decisamente” caotici. La figura che segue illustra i risultati di Laskar.
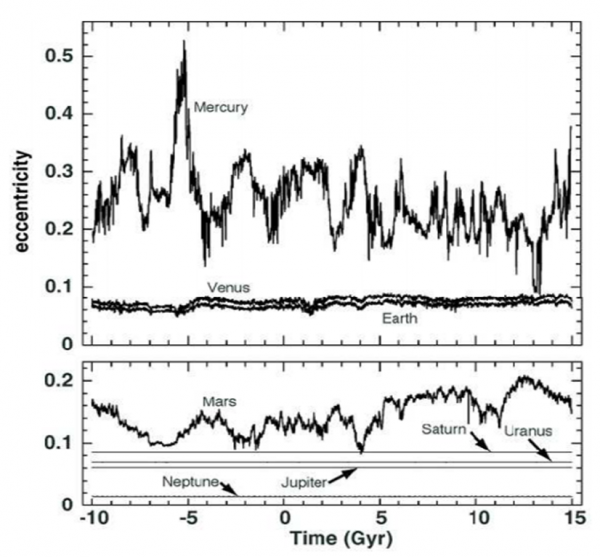
Detto in termini molto più semplici e comprensibili: “Per il Sistema Solare interno (Terra compresa) non si possono fare previsioni attendibili oltre i cento milioni di anni”.
Laskar ci rassicura sui pianeti esterni, ma ricordiamoci che gli errori ammessi finora nelle condizioni iniziali sono dell’ordine di 1/10 000 000. Sembra un’inezia, eppure lascia ancora aperta la possibilità di un regime caotico anche per loro, benché su tempi scala molto lunghi.
Il Sole diventerà una gigante rossa, ma già prima renderà invivibile la Terra (come abbiamo visto da poco). Forse ci penserà lui a rendere inutili le previsioni della meccanica celeste. Tuttavia, cento milioni di anni per la Terra non ci lascia del tutto indifferenti…
Queste recondite armonie sono ben più assordanti di quanto possano sembrare.
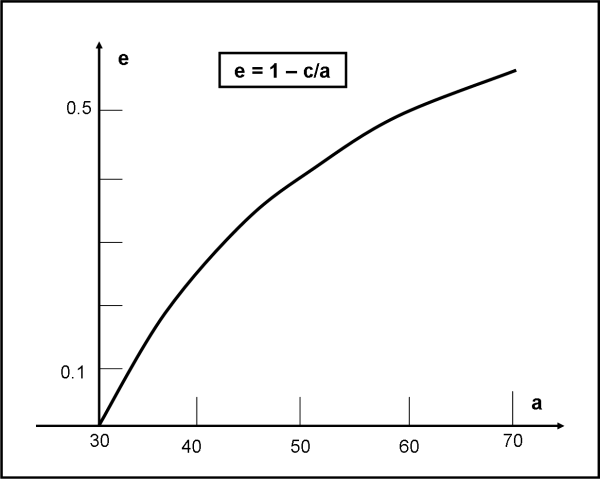
APPENDICE: Funzione che delimita i TNO scopribili. Essa non è altro che la relazione tra a ed e per un certo valore della distanza perielica p.
QUI possiamo ammirare il pentagramma disegnato dal movimento di Venere osservato dalla Terra, grazie alla risonanza 8/13 dell'orbita terrestre rispetto a quella venusiana






27 commenti
Articolo bellissimo, una sinfonia planetaria, i semiassi maggiori potrebbero essere convertiti in note e si potrebbero "ascoltare" le rivoluzioni del sistema solare, credo che qualcuno abbia già fatto qualcosa del genere...
Per rispondere alla domanda dei TNO mancanti, (ho il timore di dire una grossa stupidaggine) mi butto: troppo lontani e quindi poco luminosi?
Immagino che gli oggetti trattati abbiano inclinazioni sull'orbita diverse, se fossero TUTTI perfettamente complanari, gli effetti di risonanza sarebbero più marcati?
Il punto lagrangiano L3 completamente snobbato, è del tutto privo di oggetti? oppure occupato solo saltuariamente a causa della grande instabilità? E' il più instabile tra i punti?
Scusa per le tante domande, ma come sempre per ogni risposta esauriente si creano sempre altre domande...
Che storia intensa che ha avuto Lyapunov, anche romantica...
Nel grafico con il "?" la fascia di Kuiper è rappresentata?
caro beppe,
giustamente l'inclinazione gioca, ma su risonanze più complicate e in parte sugli effetti che ne derivano (tempi di uscita e altre modalità del genere). Per il moto medio la formula è indipendente dall'inclinazione, tuttavia essa può essere un modo per non subire effetti deleteri (molti la usano anche tra gli Hilda e i troiani). Le armonie hanno echi ancora più sottili...
L3 è snobbato, come in fondo anche L1 e L2, in quanto essendo punto instabile può al limite servire come punto di passaggio da un regime caotico a un altro. Per immetterci qualcosa dobbiamo usare strategie particolari e se lo facciamo è proprio perché vogliamo che basti poca energia per spostarlo introno a quei punti.
per beppe e teto:
sì, i TNO sono rappresentati e come! Per aiutare nella risposta, senza commentare quella di beppe, posso chiedere: "Cosa rappresenta quella linea curva attorno alla quale sembrano sistemarsi gli unici oggetti osservati?"...
cari tutti...
mi ero dimenticato di avere già scritto un articolo sui mars-crosser. Penso che possa essere interessante (ri)leggerlo:
http://www.astronomia.com/2012/09/25/il-pericolo-viene-da-marte/
Mi sa che, di tanto in tanto, potrei anche richiamare articoli precedenti, di qualche anno fa... Devo fare una bella ricerca e scegliere i più interessanti (molti di voi a quei tempi non conoscevano nemmeno il sito...).
Che ne dite?
Articolo/lezione da incorniciare e rileggere molte volte.
Soprattutto la prima parte 'Un po’ di filosofia gravitazionale e/o di gravità filosofica'
Per ora non so rispondere alla domanda, forse rileggendo tutto più volte.....
Faccio una domanda ricollegandomi al precedente articolo 'La gravità è figlia della meccanica quantistica?' e al mio intervento.
Hai scritto 'Einstein ha anche eliminato il fattore tempo, quello che limita le informazioni che sono costrette a viaggiare alla velocità della luce. La gravità non ha bisogno di messaggeri, ma agisce sul tutto e nello stesso momento: essa deforma lo spazio e il tempo e le sue pieghe più recondite spostano, deviano, modificano, all’unisono'.
Ero rimasto che nulla può superare la velocità della luce. A scuola ho preso 4 per la mia domanda, ma il dubbio mi è rimasto. Poi Ho letto dei gravitoni.
Esiste realmente una teoria/filosofia che pensa di escludere, oltre all'entanglement, il tempo nelle interazioni?
Inoltre, forse mi è sfuggito, c'è qualche tuo articolo sui punti di Lagrange L1, L2, L3, L4 e L5?
caro Walter,
La MQ, invece, vorrebbe trovare una particella che trasporta la forza di gravità, così come succede per le altre forze. Questa sarebbe l'ipotetico gravitone. In quel caso, la forza si propagherebbe alla velocità della luce e si dovrebbe riscrivere tutta la relatività o almeno adattarla alla nuova visione. In questo caso la gravità del Sole arriverebbe sulla Terra otto minuti dopo, ma dato che il Sole ha sempre la stessa massa non potremmo rendercene conto. La gravità del centro della galassia arriva sul Sole migliaia di anni dopo, ma anche in quel caso come potremmo dimostrare che quella che arriva adesso è vecchia di migliaia di anni? Bisognerebbe fare esperimenti del tipo: eliminare il Sole e vedere se la Terra gira ancora per otto minuti... Sto scherzando (in parte), ma esiste ancora questa lotta tra MQ e relatività.
Tuttavia, anche la MQ non elimina la velocità della luce e l'entanglement è una proprietà e non un'informazione che va a velocità superiore. Tuttavia, il 4 non te lo meritavi... al limite il prof. non conosce molto bene la relatività. D'altra parte c'è anche qualcos'altro che può viaggiare sicuramente più veloce della luce: lo stesso spazio che si dilata senza alcun problema. Einstein dice che niente può muoversi più veloce di c nello spazio, ma NON lo stesso spazio...
Penso di avere scritto qualcosa in astronomia.com a proposito del lobo di Roche (prova a cercare "lobo di Roche", NON "limite di Roche" che è altra cosa.). Una trattazione completa si trova soprattutto su Rosetta...
Ferma Walter....
avevo scritto qualcosa qui:
http://www.astronomia.com/2012/08/26/giuseppe-luigi-de-la-grangia-e-i-suoi-punti-speciali/
Grazie per la risposta.
A proposito di Rosetta tempo fa sono stato sia alla Rizzoli che alla Feltrinelli, a Milano, ma non sono riuscito né a trovarlo né a prenotarlo.
Via Internet non mi fido
Splendido articolo davvero, mi ha dato molto su cio riflettere.
 ).
).
La cosa che piú mi ha impressionato é il fatto che noi non riusciamo a trovare una soluzione a un problema e ci scervelliamo per venirne a capo.........e invece l'universo ci mostra impietosamente che la soluzione esiste e che per lui é semplice e naturale
E' un po' come se fosse il nostro maestro che ci vuole aiutare ad arrivare alla soluzione, ma stimolandoci a farlo da soli e con il ragionamento, non facendoci imparare a memoria le regole.
Comunque piú leggo sull'universo e le sue meraviglie e piú ho la sensazione che tutto dipenda dalla mancanza dello "0" (giusto per tornare ai nostri amici
Per i TNO direi che lo spazio nel grafico é vuoto perché....non é vuoto! o almeno non sempre
Grazie per l'articolo Enzo e per i ricordi che hai condiviso......é gia diventato uno dei miei preferiti!
Non dici male Andrea... lo zero è irraggiungibile e certi processi ne avrebbero bisogno per dare risposte esatte. Forse addirittura il caos (lì, però, c'è il problema dell'inifinito: tante sono le variabili che bisognerebbe tenere in conto...).

Per i TNO sei stato troppo sibillino: CHIARISCI MEGLIO IL TUO PENSIERO!!!
caro Walter,
avo pagato per un anno la feltrinelli per avere il libro nelle librerie. Tuttavia, mi costava decisamente di più di quello che riuscivo a ricavare (10 a 1). Io ho sempre comprato via internet, usando una carta prepagata con sù poche decine di euro. La consegna è molto efficiente, e i rischi si annullano per la limitatezza di ciò che contiene la carta...
Beh mi viene da pensare che se la proporzione tra il semiasse maggiore e l'eccentricitá va oltre a un certo punto, che immagino sia la curva, gli eventuali corpi nel punto dell'orbita piú stretto vadano o a impattare sui pianeti o comunque risentano in modo troppo marcato della loro gravitá per fare in modo che possano rimanere in quella zona......cosí a naso eh, ma probabilmente é una stupidaggine
Cerco di rispondere meglio alla domanda, più l'eccentricità è bassa, più grande sarà l'asse minore, quindi più lontano dal Sole e dalla Terra perciò difficilmente individuabile. L'eccentricità è il rapporto fra la differenza dei semiassi rispetto alla somma degli stessi, e= 0,5 vuol dire che il semiasse maggiore è tre volte il semiasse minore.
no...Andrea gli impatti non c'entrano..
caro Beppe attento a non confondere semiassi con altre cose.... L'idea va però nel verso giusto.
la curva è una funzione molto semplice... che si può scrivere tenendo presente che oltre a una certa distanza dal Sole non riusciamo a vedere. Qual'è questa distanza? E come si può esprimere la e in funzione della a attraverso questa distanza?
La butto lì, la funzione approssimata dovrebbe essere circa 50/(1-e), ponendo la distanza massima di visibilità circa 50 UA, aumentando l'eccentricità si possono osservare anche oggetti con semiasse molto elevati se presentano un'orbita molto eccentrica, come per esempio le comete, naturalmente per un breve periodo in prossimità del perielio..
Accidenti Enzo,
sono in ritardo con gli articoli perchè dopo Natale abbiamo avuto due giorni di black-out... Ora devo recuperare...
Giorgia
Opps! naturalmente ho invertito gli assi semiasse maggiore in funzione dell'eccentricità.
la funzione opposta è e= 1-(semiasse maggiore/50)
caro beppe, dai che ci sei quasi.. però diamo un nome alle cose. Quella distanza di cui parli e che metti, ad esempio, uguale a 50 non è altro che il PERIELIO (non una funzione approssimata...). Esso vale proprio:
p = a(1-e).... da cui ricavando e in funzione di a si ha:
p = a -ae
ae = a - p
e = 1 - p/a
se a cresce p/a diventa più piccolo e cresce quindi l'eccentricità che tende a 1. (p deve essere sempre minore di a per definizione di perielio).
Se il semiasse cresce troppo gli oggetti si possono vedere solo al perielio e se questi hanno enormi semiasse devono avere eccentricità molto alte. Nella zona vuota ci sono oggetti con grandi semiassi e modeste eccentricità per i quali la distanza perielica è troppo grande per i telescopi. Ovviamente gli oggetti su orbite circolari si vedono solo se il semiasse è uguale a p, infatti:
e = 1 -1 = 0
Tra un po' parleremo a fondo delle coniche... La matematica va impostata rigorosamente e non cercando una relazione più o meno empirica che sembra andar bene per il nostro problema. Comunque, l'idea era quella giusta!
Concludendo: la curva non è altro che la relazione tra e ed a impostando un perielio costante. Cambiando il perielio avremmo un'altra curva....
va bene, dai sette più!!!!
cara Giorgia,
non preoccuparti... vado tre giorni in toscana per Capodanno e non poso dedicarmi al blog. Hai tempo per recuperare. E poi starò zitto dal 21 gennaio al 16 febbraio (non porto il PC dato che voglio proprio staccare...) e mi sa che non solo recupererete, ma forse vi dimenticherete di me... Speriamo di no!
NB: In fondo all'articolo ho inserito la funzione che determina la curva relativa ai TNO. Quanto vale il suo limite per a che tende a infinito? Tanto per tenere le funzioni sotto controllo... Ho posto p = 30 UA.
Ciao Enzo,
mi stai proprio viziando con tutti questi articoli di meccanica celeste…
Provo a rispondere alla domanda sui TNO…
Probabilmente quella zona rappresenta il luogo “critico” in cui gli oggetti non riescono a stabilizzare la propria orbita e vengono cacciati … Diciamo che sono il contrario dei punti Lagragiani.
Non ti preoccupare che nessuno si dimenticherà di te, garantito...
Giorgia
ciao Giorgia,
riguardo ai TNO... la riposta l'ho già data qualche commento fa e ho aggiunto una figura al fondo dell'articolo. No, i TNO ci sono ma non li possiamo vedere perché il loro perielio è troppo lontano per i nostri telescopi.
Ti ringrazio....
Bellissimo articolo caro Enzo! Anche se dal cellulare ci ho messo un po a leggerlo devo dire che mi e'proprio piaciuto...mi rimangono un po' di dubbi sulla risonanza costruttiva...mentre si intuisce bene quella distruttiva faccio ancora fatica a capire appieno quella costruttiva come riesca ad avere quell'effetto...
Grazie comunque per l'articolo!
Grazie.
Articolo illuminante anche se ancora non completamente "digerito"
Per quanto mi riguarda, l'idea di riproporre articoli del passato è ottima.
e= lim a → ∞ (1-c/a)=1
ottimo Concetto!
Caro Lampo,
per quella costruttiva devi pensare che rimangono solo gli oggetti che si trovano sempre in posizioni di sicurezza con Giove. I Troiani lungo tutta l'orbita sono stati cacciati e sono rimasti solo quelli in posizione particolare di equilibrio... Analogamente per gli Hilda...
BUON ANNO e bacioni ad Ariana!!!!!!!!!!!!!!!!!!!!
Grazie Enzo...! Quella dei troiani, in risonanza 1/1 e' abbastanza comprensibile...sono le altre che mi lasciano ancora qualche dubbio...ad esempio...puo' esistere una risonanza costruttiva per gli anelli di saturno? Una parte di anello piu' fitta causata da una risonanza? Ti spieghero' meglio poi a voce...ora andiamo a mangiare in un ristorante di comida preispanica...chissa' cosa ci prepareranno! L'armadillo pare essere il piatto forte...
Un abbraccio a te e Gianna da me e Mariana...buon anno!