Categorie: Matematica
Tags: aree cerchio circonferenza corde geometria quiz soluzione
Scritto da: Vincenzo Zappalà
Commenti:2
Soluzione del raggio ottenuto attraverso due corde **
Ecco la soluzione puramente geometrica, anche se, come sempre, il risultato si poteva ottenere in modo analitico.
Leandro ha sicuramente individuato la strategia, ma poi ha girato un po' intorno alla soluzione più semplice. Gianluca ha risolto il caso più facile, facendo passare le corde per il centro. MarcoC l'ha un po' complicata e si è fermato a metà strada.
Seguiamo pure la figura proposta da Leandro... (Fig. 1)
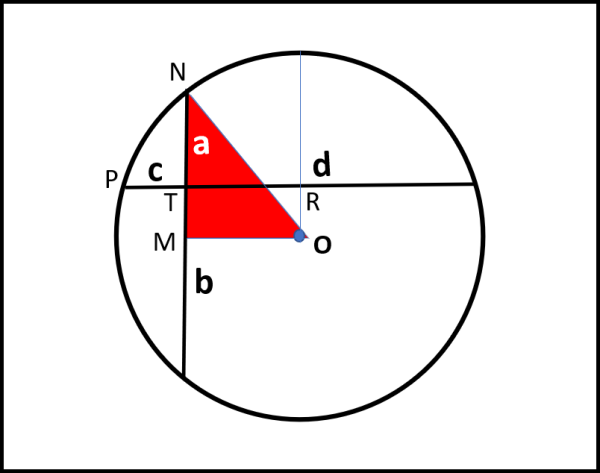
Sfruttiamo la proprietà ben nota che qualsiasi perpendicolare tracciata dal centro a una qualsiasi corda la divide a metà (facilissimamente dimostrabile attraverso un semplice triangolo isoscele).
Abbiamo subito, perciò, che:
MN = (a + b)/2
PR = (c + d)/2
MO = TR = (c + d)/2 - c = (d - c)/2
Adesso, possiamo considerare il triangolo rettangolo OMN e applicare il teorema di Pitagora:
ON2 = r2 = ((a + b)/2)2 + ((d - c)/2)2
r2 = (a + b)2/4 + (d - c)2/4
4r2 = (a + b)2 + (d - c)2 = a2 + b2 + 2ab + d2 + c2 - 2dc .... (1)
Beh... non sembrerebbe troppo "compatta", ma basta ricordare un'altra proprietà delle corde di una circonferenza: se due corde s'intersecano tra loro si dividono ciascuna in due segmenti il cui prodotto è uguale. Questo vale per qualsiasi inclinazione delle corde e deriva dal teorema delle corde che si dimostra in un baleno (Fig. 2).
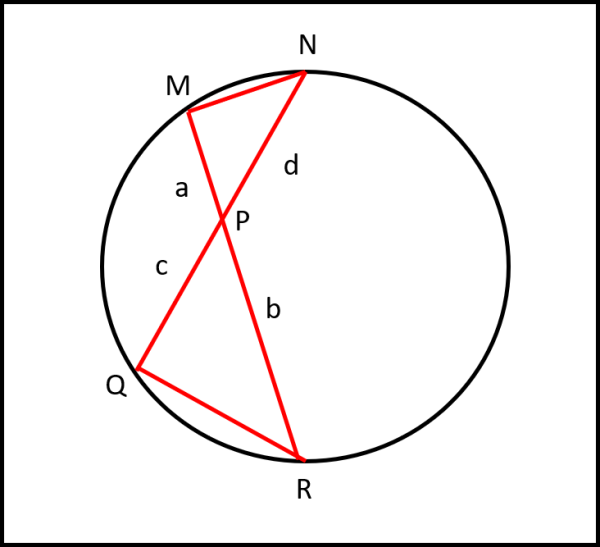
I due triangoli QRP e MNP sono simili aventi i tre angoli uguali. Quelli in P sono opposti al vertice e quelli in N e in R sono angoli alla circonferenza dello stesso arco MQ. Possiamo allora scrivere la proporzione:
a : c = d: b
ossia:
ab = cd
Ma, applicando questa relazione alle nostre due corde del quiz, si ha proprio
ab = dc
In poche parole:
ab - cd = 2ab - 2cd =0
e spariscono i doppi prodotti della (1). In definitiva si ha:
4r2 = a2 + b2 + c2 +d2
Prima di terminare, vediamo come questa relazione si agganci perfettamente all'area del cerchio di partenza. Spostiamo il 4 e moltiplichiamo tutto per π, ottenendo:
πr2 = π(a/2)2 +π(b/2)2 +π(c/2)2 +π(d/2)2
Il che ci dice che l'area del cerchio è uguale alla somma delle aree dei cerchi che hanno come raggio i quattro segmenti delle corde, proprio come mostra la Fig. 3. Un bel gioco di incastri... che potrebbe portare a tante divagazioni sul tema...







2 commenti
tormento finito!