Questo articolo è stato inserito in "Il moto dei pianeti secondo Feynman", al quale si rimanda per una trattazione completa dell'argomento

 

Abbiamo costruito il diagramma delle velocità corrispondente a una traiettoria che segua la seconda legge di Keplero e in cui la forza di attrazione vada con l'inverso della distanza al quadrato. Tuttavia, non  sappiamo ancora che traiettoria sia e, soprattutto, non abbiamo ancora dimostrato che il diagramma delle velocità sia proprio un poligono regolare. Iniziamo con quest'ultimo problema.

Ribadiamo le condizioni necessarie per avere un poligono regolare: tutti i lati devono avere uguale lunghezza e tutti gli angoli dei vari spigoli devono avere la stessa ampiezza. Noi, invece, abbiamo un bel poligono che si chiude, ma è stato costruito sulla base delle distanze (velocità) sempre diverse, fatte partire da un punto che, comunque, non potrà mai essere il centro del cerchio circoscritto al poligono (sempre che esista). Riprendiamo la poligonale costruita la volta scorsa (Fig. 18).

I vari lati sono proporzionali a dv. Tuttavia, questi valori cambiano continuamente, in quanto la costruzione si è basata su triangoli tali da avere sempre la stessa area a parità di tempo trascorso (seconda legge di Keplero).

Cambiamo, allora, la procedura e consideriamo triangoli che abbiano lo stesso angolo al Sole  θ. Si ottiene, per la traiettoria del pianeta, una poligonale come quella di Fig. 19.

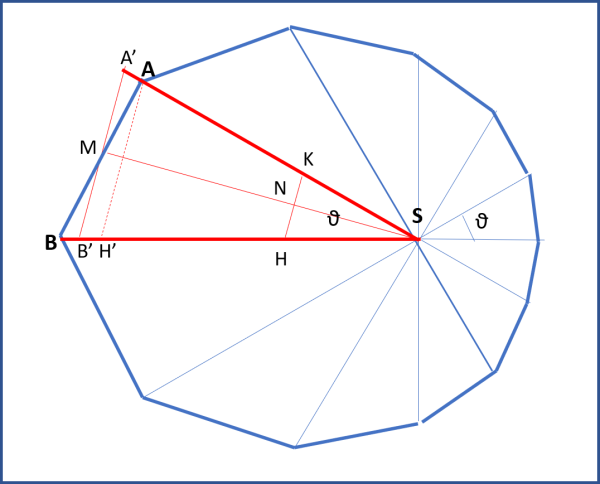
Ovviamente, le aree non sono più uguali e quindi tale non è nemmeno il tempo impiegato a spazzarle, dato che sappiamo che vale:

Area ∝ dt

Ossia più l'area è grande e più tempo impiegherà il pianeta a spazzare il triangolo.

Occupiamoci, allora, del triangolo ABS (ma il discorso vale per tutti). Esso tutto è fuorché isoscele, tuttavia possiamo tracciare un segmento  HK perpendicolare alla bisettrice dell'angolo θ (ASB). Facciamo  scorrere questo segmento (allungandolo gradatamente) fino a farlo arrivare in AH'. Poi, proseguiamo fino a che l'area del triangolino AA'M non sia uguale all'area del triangolo MBB'.  Per costruzione A'B' è perpendicolare a SM e il triangolo A'B'S è isoscele. Ne segue che l'area del triangolo ABS è uguale a quella del triangolo isoscele A'B'S, di cui SM è l'altezza.

Calcoliamo l'area del triangolo  A'B'S = ABS

A_ABS = 1/2 A'B'· SM                  .... (6)

Il triangolo A'B'S' è simile al triangolo HKS, per cui possiamo scrivere:

KH: A’B’ = SN: SM

A'B' = SM·KH/SN

Sostituendo nella (6) abbiamo:

A_ABS = (1/2KH/SN)SM²  ∝ SM² = R²            .... (7)

In altre parole, l'area spazzata è proporzionale al quadrato della distanza dal Sole  R = SM.

Ed eccoci al piccolo grande capolavoro di Feynman...

Noi sappiamo che per la forza diretta verso il Sole vale:

F = ma  ∝  a = dv/dt ∝ 1/R²

ossia:

dt ∝ dv R²           .... (8)

ma sappiamo anche che:

A_ABS  ∝ dt

e, quindi, dalla (7), che:

dt ∝ R²

Sostituendo dt nella (8), otteniamo:

R² ∝ dv R²

ossia:

dv ∝ 1

In parole più semplici dv è una COSTANTE. E questo vale per qualsiasi punto della traiettoria per come l'abbiamo costruita. L'importante è che i triangoli abbiano sempre lo stesso angolo al Sole  θ. Ovviamente, più l'angolo è piccolo e più diminuiscono le aree dei triangoli e sempre più la poligonale si avvicina a una curva.

Si può allora ottenere il diagramma delle velocità sostituendo ai triangoli di area uguale, triangoli con lo stesso angolo al Sole. Questa volta, però, il poligono che ne consegue ha tutti lati (dv) uguali tra di loro, così come gli angoli supplementari a quelli degli spigoli in quanto dv è sempre diretto verso il Sole e quindi l'angolo tra di loro deve essere uguale a θ . Ecco il nuovo diagramma delle velocità mostrato a destra in Fig. 20.

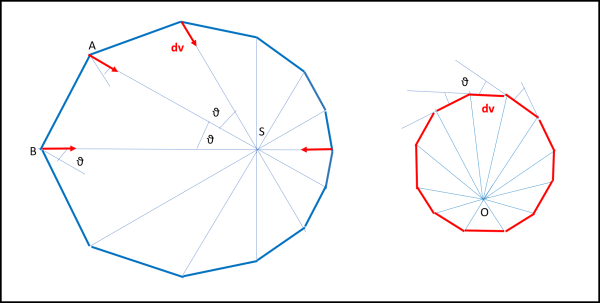
Il concetto è molto chiaro e Feynman è riuscito a costruire, finalmente, un diagramma delle velocità che sia un poligono regolare e che quindi possa portare (aumentando sempre più i lati e rimpicciolendo i triangoli) a un cerchio perfetto. E' però interessante vedere come costruire in pratica questo diagramma... io presento due metodi, di cui uno del tutto personale, ma che in pratica dicono la stessa cosa... Utilizziamo la Fig. 21.

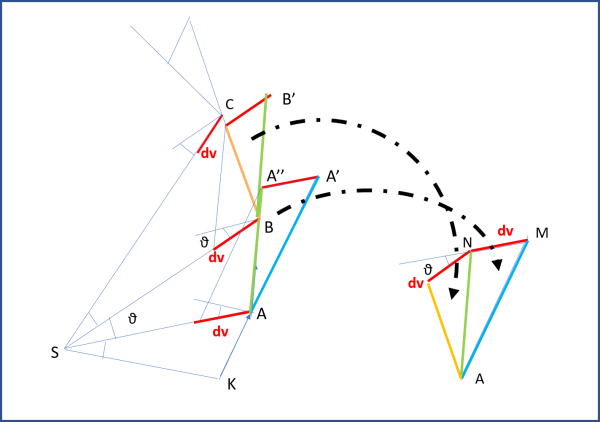
Attenzione: Le velocità sono sempre dirette lungo i lati del poligono delle posizioni (a sinistra), continuando a cambiare da vertice a vertice, dato che cambia sia il dt relativo a ciascuna area, sia lo spazio percorso (il lato).  Ciò che non cambia mai è il dv, ossia la differenza tra le velocità di ogni singolo lato del poligono. Essa è stata dimostrata essere una costante.

Allora, basta prendere un segmento parallelo a KA e uno parallelo ad AB (poligonale di sinistra, quella delle posizioni), Farli partire dallo stesso punto A, che rimarrà sempre il punto di origine, prolungare KA fino ad  AA' e AB fino ad AA" in modo che A'A" uguagli dv (in modulo, e direzione) che deve rimanere costante. In  tal modo abbiamo costruito il triangolo AMN del diagramma delle velocità che è uguale a quello AA'A" del diagramma orbitale. Poi passiamo al punto B del diagramma di sinistra e tracciamo le due direzioni delle velocità (quella che arriva in B e che è la velocità gialla e quella che parte da B, verde, e che è deviata a causa dell'attrazione solare) fino a formare di nuovo una differenza tra le due che sia proprio dv. Si ottiene il triangolo BCB' che può essere spostato nel digramma delle velocità, sicuri che AN coincida con BB' (E' la stessa velocità di arrivo e di partenza da B). E via dicendo fino a completare il diagramma di destra che è proprio quello delle velocità.

Oppure, come fa Feynman, partire direttamente dal diagramma delle velocità (Fig. 22), disegnando un segmento pari a dv e parallelo a quello del diagramma delle posizioni (a destra).

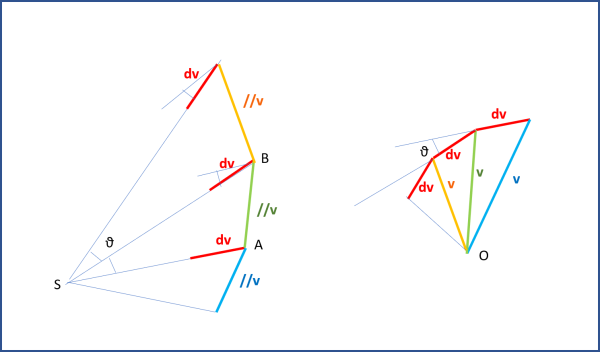
Dai suoi estremi tracciare le parallele alle due velocità (blu e verde) relative al punto A del diagramma orbitale (a destra). Le due parallele si incontrano in un punto O. Di seguito al primo dv inserisco il secondo dv parallelo a quello ricavato dal diagramma di destra. Dal suo estremo di sinistra traccio la parallela alla velocità gialla di B. E via dicendo... Nuovamente siamo sicuri che tutte le dv sono uguali (per costruzione) e anche gli angoli del poligono delle velocità dato che tra le dv l'angolo è sempre lo stesso.

Scegliete voi il metodo che preferite e costruitevi l'intero diagramma delle velocità.

Attenzione, però... non vi venga in mente di dire che l'angolo θ è uguale all'angolo in O del diagramma! L'angolo θ è qualcosa di differente (fortunatamente!).

Ricapitoliamo, disegnando la poligonale delle velocità completa in Fig. 23.

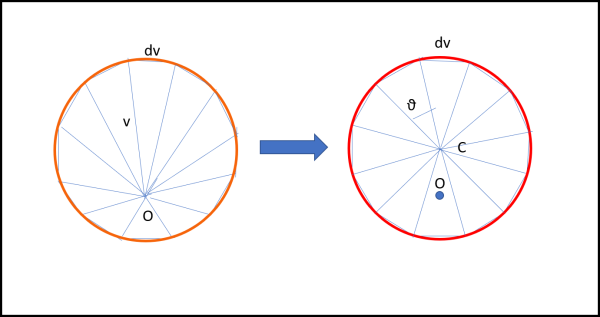
Sappiamo ormai -e lo abbiamo dimostrato- che il poligono è regolare e che può essere ricondotto a un cerchio di cui O non è assolutamente il centro. Disegniamo, invece, il centro C del cerchio che ormai siamo sicuri che esista e congiungiamolo con tutti i punti del poligono. Nel caso della Fig. 23 questi punti sono 12 tanti come quelli che ci sono serviti per costruire il diagramma delle posizioni (orbitale). Otteniamo, per costruzione,  12 triangoli isosceli tutti uguali. L'angolo al centro è quindi 360°/12. Ma anche i triangoli dell'orbita sono 12 a hanno lo stesso angolo al Sole θ per costruzione. 12 di questi angoli fanno un angolo giro e quindi  devono essere uguali e  360°/12 ciascuno. In poche e banali parole: l'angolo θ è uguale all'angolo al centro del poligono delle velocità.

Qualsiasi orbita che segua la seconda legge di Keplero e la forza di gravità (che deriva dalla terza legge) deve portare a un diagramma delle velocità che sia un poligono regolare e quindi, per θ tendente a zero, riducibile a una circonferenza.

Bene... non ci resta che fare l'ultimo passo. Abbiamo a disposizione la circonferenza delle velocità e vogliamo dimostrare che ciò implica che la traiettoria che ci è servita per costruirla è proprio un'ellisse.