Categorie: Meccanica Celeste
Tags: costruzione ellisse diagramma velocità Feynman percorso della luce riflessione traiettoria dei pianeti
Scritto da: Vincenzo Zappalà
Commenti:0
Keplero e Newton rivisitati da Feynman. 5 : la curva è proprio un'ellisse! **
Questo articolo è stato inserito in "Il moto dei pianeti secondo Feynman", al quale si rimanda per una trattazione completa dell'argomento
Nella puntata precedente eravamo riusciti a costruire il diagramma delle velocità basandoci sui primi due principi della dinamica e sulle prime due leggi di Keplero. Non ci resta che utilizzare questo geniale diagramma per dimostrare che la curva della traiettoria è proprio un'ellisse. Chi ha seguito i vari articoli si sarà già accorto che il diagramma delle velocità assomiglia in tutto e per tutto al cerchio iniziale della prima puntata. Basterebbe applicare a lui il procedimento usato allora e salterebbe fuori l'ellisse.
Tuttavia, arriviamo alla soluzione con la massima calma e attenzione.
In Fig. 24, disegniamo a sinistra il diagramma delle velocità e a destra la traiettoria del movimento di un pianeta che segua la seconda legge di Keplero e che subisca una forza di attrazione da parte del Sole diretta nella sua direzione e che vada con l'inverso del quadrato della distanza (legge che abbiamo determinato attraverso la terza legge di Keplero).
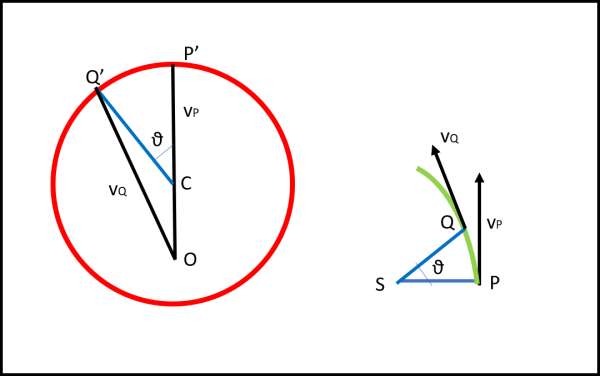
Abbiamo anche dimostrato che l'angolo al centro θ tra gli estremi delle velocità di P e di Q (P' e Q') è uguale all'angolo al Sole tra i due punti P e Q. Ricordiamo anche che le linee da O (punto eccentrico che ci ha permesso di costruire il cerchio delle velocità) ai punti della circonferenza sono proprio le velocità dei vari punti della traiettoria. In altre parole, facendo variare il punto sul cerchio delle velocità, i segmenti OP', OQ' ecc. descrivono le tangenti (direzione delle velocità) dei punti P e Q sul diagramma orbitale. Un giro completo del punto sulla circonferenza del diagramma delle velocità equivale a un'orbita completa.
Praticamente, dobbiamo dimostrare che la traiettoria che ha come tangente in ogni suo punto la velocità del diagramma delle velocità è proprio un'ellisse.
Per ottenere il risultato voluto, Feynman fa un'operazione banalissima, ma geniale: ruota il diagramma-cerchio delle velocità di 90 ° verso destra in modo che i lati dell’angolo θ risultino paralleli tra un diagramma e l’altro. La linea indicata con “vP”, che era parallela alla velocità in P, ora è perpendicolare (Fig. 25).
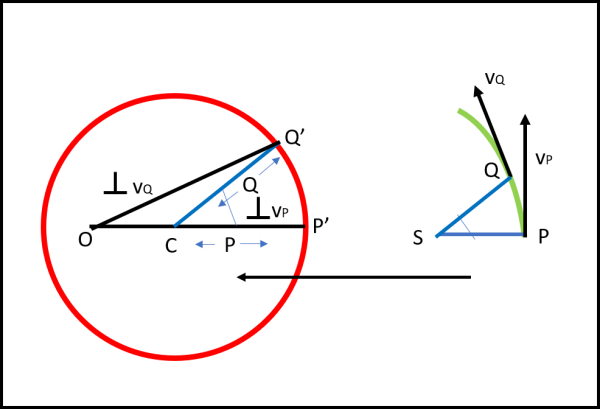
Il punto P, per il quale la velocità è massima, deve stare su SP , parallelo a CP', e deve avere una velocità che è data dalla perpendicolare alla velocità relativa a P' nel cerchio delle velocità, dato che è stato ruotato di 90°.Analogamente il punto Q deve stare sulla parallela a CQ', passante per il Sole (l'angolo θ è lo stesso) e deve avere come tangente la perpendicolare alla velocità ruotata OQ'. Possiamo tranquillamente traslare il diagramma di destra fino a fare coincidere S con C. Non possiamo, però, sapere le distanze CP e CQ.
Tuttavia, questo non è un problema, in quanto è comunque possibile costruire l'orbita che segue le due proprietà appena richiamate, del tutto sufficienti a disegnare una traiettoria che sia come forma e direzione simile a quella reale. Conoscendo la distanza dal Sole di un solo punto dell'orbita reale sarà poi possibile scalare la nostra curva fino a farla passare per quel punto. In tal modo la traiettoria sarà sicuramente quella percorsa dal pianeta che segue le proprietà riassunte nella costruzione del cerchio delle velocità.
A questo punto possiamo ripetere pari pari la costruzione del primo capitolo, lavorando direttamente nel diagramma delle velocità (Fig. 26).
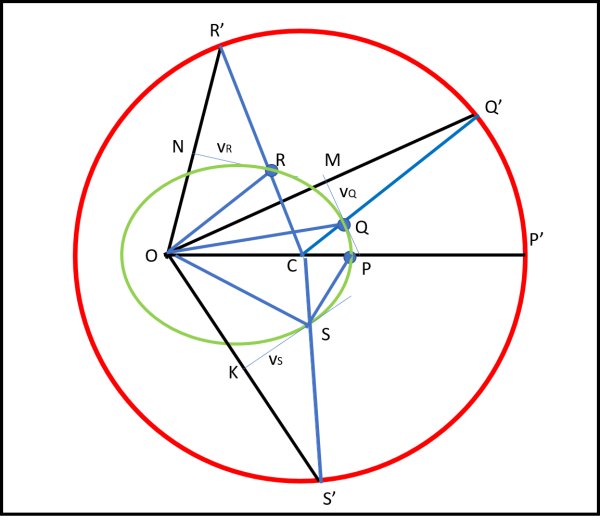
Uniamo il centro O con un punto qualsiasi della circonferenza, ad esempio Q'. Dal punto di mezzo M del segmento OQ' tracciamo la perpendicolare, parallela alla velocità del corrispondente punto Q dell'orbita (per costruzione, dato che abbiamo ruotato di 90° il diagramma). Uniamo C con Q'. Il punto intersezione tra CQ' e la perpendicolare tracciata prima deve essere un punto dell'orbita, in quanto ha la giusta tangente e il giusto angolo al Sole QCP (θ).
Resta solo da verificare se è un'ellisse... Calcoliamo la somma delle due distanze di Q dal punto O e dal punto C e controlliamo che essa dia sempre lo stesso risultato al variare di Q. Costruiamo il punto R con la stessa procedura e otteniamo i segmenti RC e RO. Sommiamoli assieme e confrontiamoli con la somma precedente. Prima, però, dobbiamo accertare che i triangoli rettangoli QMO e MQQ' siano uguali. Lo sono senz'altro avendo due lati uguali (OM e MQ') per costruzione e MQ in comune. Ne segue che QQ' = QO e, analogamente, RR' = OR. Possiamo, allora scrivere:
CQ + OQ = CQ + QQ' = raggio del cerchio delle velocità
RC + OR = RC + RR' = raggio del cerchio delle velocità.
La curva descritta da un pianeta attorno al Sole deve, perciò, essere un'ellisse, con i fuochi in O e in C.
Prima di terminare, notiamo un fatto importante legato all'ellisse ed estremamente importante per tutta la QED di Feynman, dato che si collega direttamente alla distanza minima percorsa dalla luce, ossia al principio di Fermat che dice: " ...di tutti i possibili cammini che un raggio di luce può percorrere per andare da un punto a un altro, esso segue il cammino che richiede il tempo più breve". Questo principio ha come conseguenza il cammino di un raggio di luce riflesso da uno specchio che trova il suo cammino più breve quando l'angolo di incidenza è uguale all'angolo di riflessione.
Consideriamo la Fig. 27, dove è riportata la nostra ellisse appena costruita (abbiamo già scritto F e F' al posto di O e C).
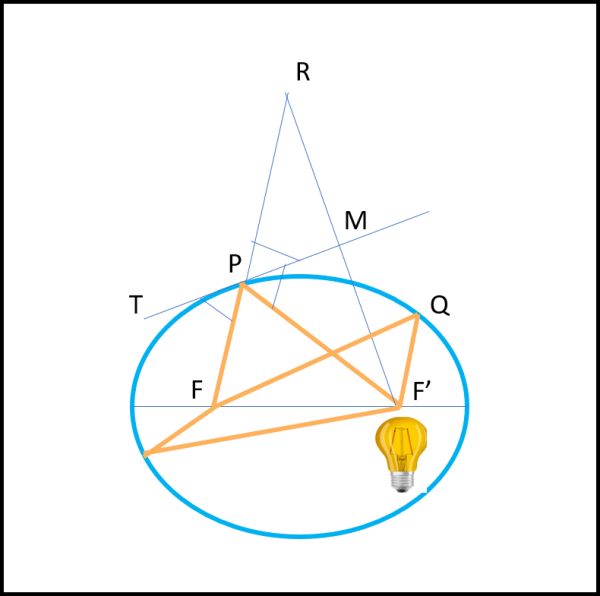
Manteniamo anche la costruzione del punto P e mettiamo una lampadina in F'. Rivestiamo di materiale riflettente l'interno della nostra ellisse. Vediamo cosa ci combina la traiettoria F'PF. Essa colpisce l'ellisse in P, la cui tangente è proprio TM. Sappiamo che RPM = MPF' (l'abbiamo appena dimostrato), ma dobbiamo concludere che anche TPF = RPM (angoli opposti al vertice). Ne segue che TPF = MPF'. Ma, allora, il raggio di luce FPF' si riflette sulla ellisse in modo che l'angolo di incidenza sia uguale a quello di riflessione. In altre parole è il percorso minimo della luce per andare da F a F'. Lo stesso, capita, però, anche per qualsiasi altro punto dell'ellisse, che risulta quindi il luogo dei punti di riflessione della luce che parte da F' e viene raccolta in F (e viceversa). Un altro fantastico modo "fisico" per definire un'ellisse.





