Soluzione al quiz dell'urto ammortizzato

Soluzione al quiz sull'urto ammortizzato

Per rispondere ai primi tre quesiti del quiz conviene seguire la via "energetica".

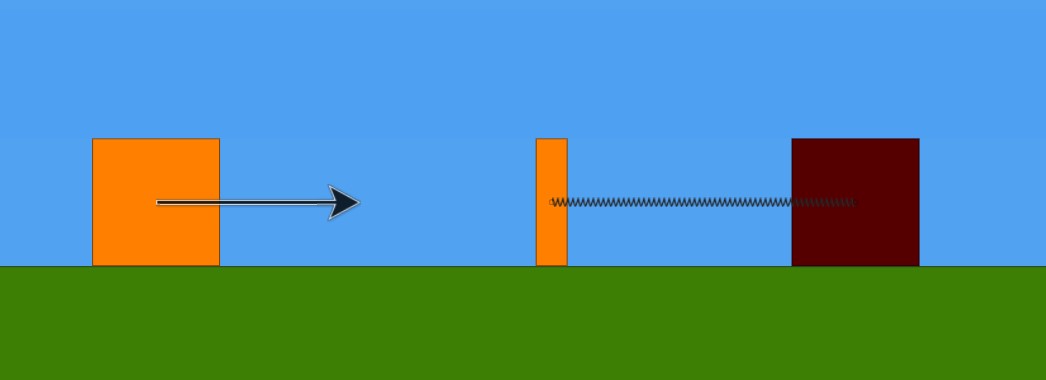
Nella fase iniziale, cioè quando abbiamo solo la massa m1 in moto rettilineo uniforme con velocità v1, l'energia meccanica del sistema è data dalla sola energia cinetica posseduta dalla massa m1:

$E_{m}=K=\frac{1}{2}m_{1}v_{1}^{2}$

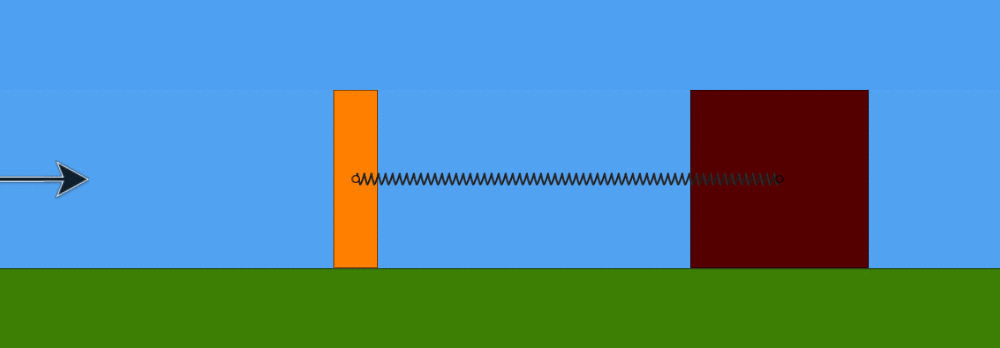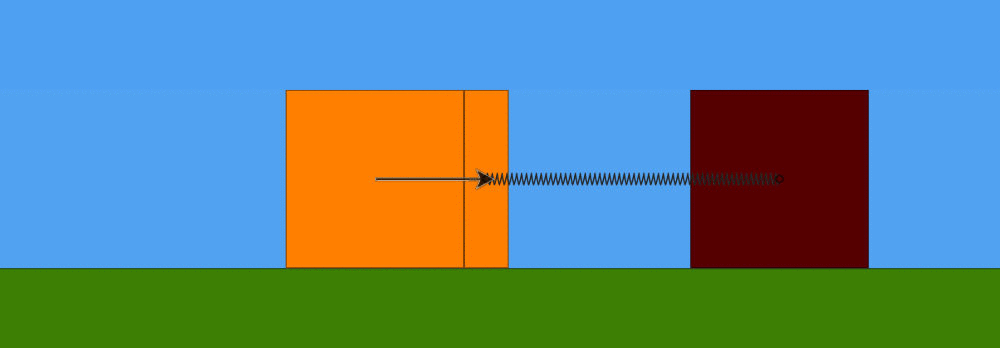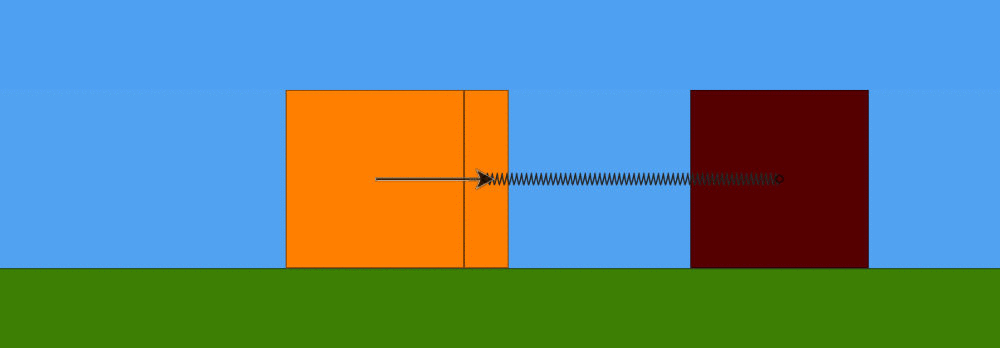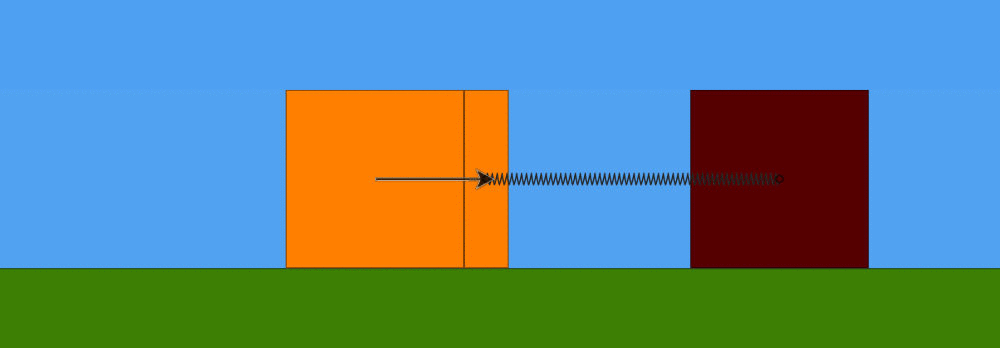
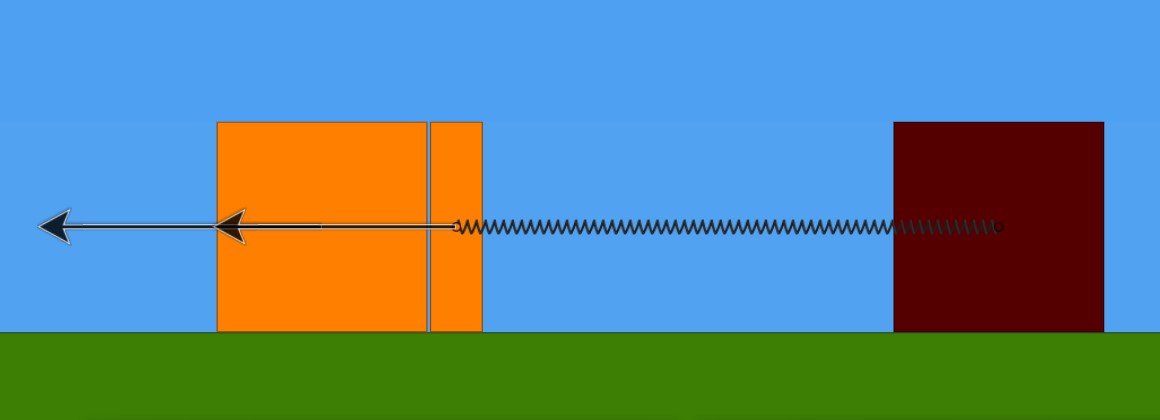
Osserviamo ora , "alla moviola", l'evolversi del sistema. Nell'istante in cui la massa m1 entra in contatto con la massa m2 , poiché l'urto è, per ipotesi, perfettamente anelastico, le due masse m1 ed m2 iniziamo a muoversi all'unisono verso destra, cioè restando unite e con la stessa velocità v2, diversa da quella con cui, prima dell'urto, si stava muovendo la sola massa m1. Nella seguente animazione , realizzata con Algodoo (software per simulazione problemi di fisica nel piano), si nota la riduzione del modulo della velocità immediatamente dopo l'urto:

Vale la legge di conservazione della quantità di moto, secondo la quale la quantità di moto prima dell'urto resta uguale a quella immediatamente dopo l'urto. Possiamo, dunque, scrivere:

$m_{1}v_{1}=(m1+m2)v_{2}$

da cui ricaviamo

$v_{2}=\frac{m_{1}}{(m_{1}+m_{2})}v_{1}$ (1)

Un istante dopo l'urto , procedendo ora le due masse insieme verso destra, la molla alla cui estremità è connessa la massa m2 inizia a comprimersi. Le due masse , dunque, iniziano a risentire della forza elastica esercitata dalla molla, forza che si oppone al loro movimento, quindi ne rallenta il moto fino a fermarlo. Quando le due masse si fermano ? Riecco la considerazione "energetica": quando l'energia cinetica posseduta dalle due masse insieme dopo l'urto si trasforma interamente in energia potenziale elastica immagazzinata nella molla (in compressione). Determiniamo allora queste due grandezze.

L'energia cinetica delle due masse insieme dopo l'urto è:

$K_{2}=\frac{1}{2}(m_{1}+m_{2})v_{2}^{2}$

L'energia potenziale elastica immagazzinata in una molla compressa di un tratto ("elongazione") $\Delta x$ è:

$U_{e}=\frac{1}{2}k\Delta x^{2}$

dove k è la costante elastica della molla.

Uguagliando l'energia cinetica con l'energia potenziale elastica otteniamo:

$\Delta x=v_{2}\sqrt{\frac{(m_{1}+m_{2})}{k}}$ (2)

con v2 data dalla (1).

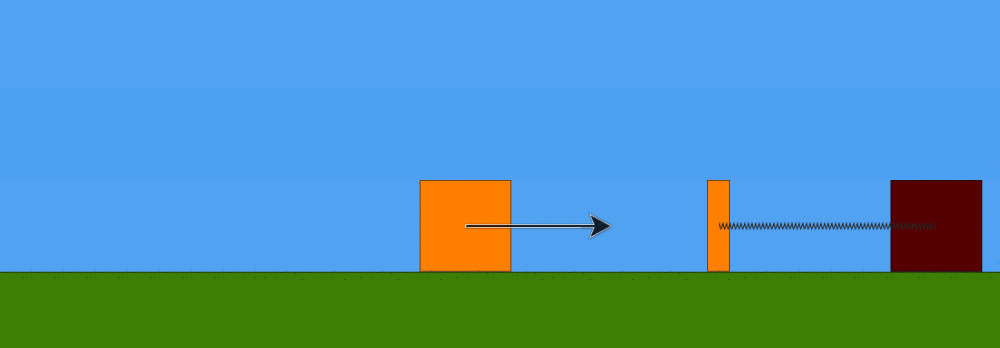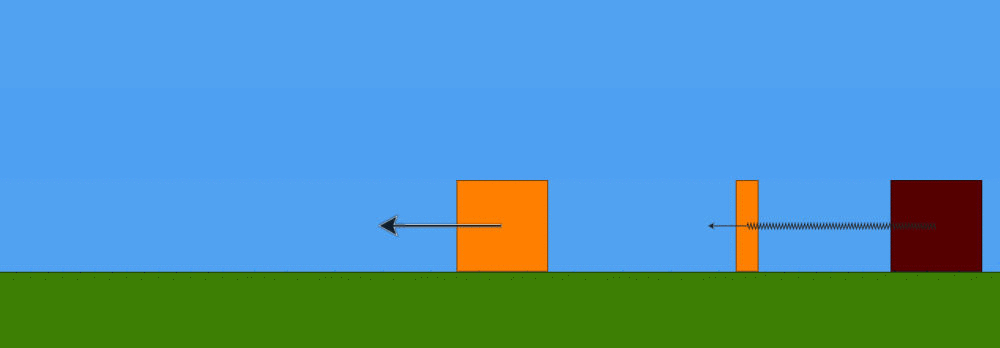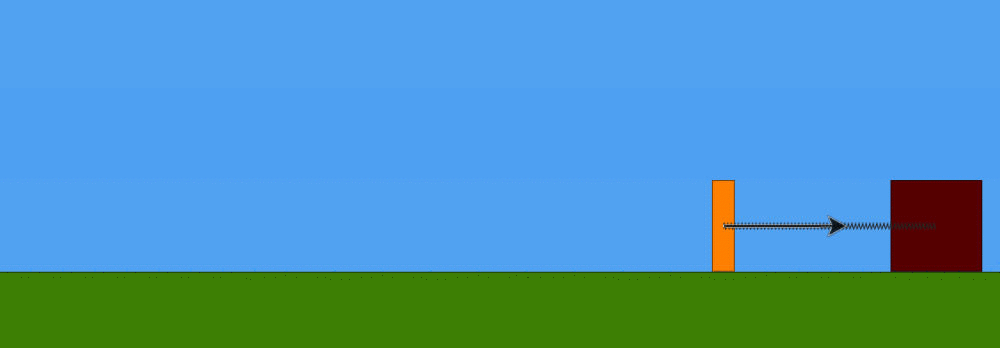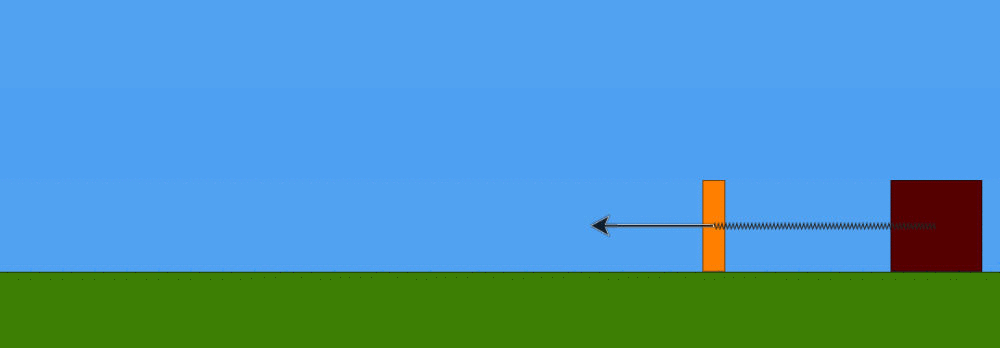
All'istante in cui le masse avranno percorso il tratto $\Delta x$ , le troveremo ferme. Ma la forza elastica della molla (che è compressa) non è sparita, anzi, da questo momento in poi spinge le due masse verso sinistra. Le due masse, in pratica, dopo essersi arrestate, ricominciano a muoversi ma in verso opposto, cioè verso sinistra, e sempre insieme. Esse continuano ad accelerare fino a quando tutta l'energia potenziale elastica non si sarà ritrasformata in energia cinetica. E' intuitivo che ciò avvenga quando la molla torna alla sua lunghezza a riposto , quella cioè che aveva all'inizio , quando la massa m1 era in quiete. In questo preciso istante, la velocità delle due masse insieme tornerà ad essere data dalla (1) ma con verso opposto. In questo stesso istante avviene anche un altro fatto importante: la massa m1 si separa nuovamente dalla massa m2 connessa alla molla.

Questo avviene perché, continuando a muoversi verso sinistra, ad un certo punto la forza elastica della molla trattiene la massa m2, che è connessa alla molla, ma non più la m1, che è libera di scorrere via verso sinistra. Da questo istante in poi, quindi, la massa m2 torna ad essere sola, come la massa m1, ma continuando a risentire della forza di richiamo elastico della molla. Quale sarà, allora, lo spostamento massimo della massa m2 dalla posizione di equilibrio ? Considerazione energetica: tale spostamento massimo è quello in corrispondenza del quale l'energia cinetica posseduta dalla massa m2 si sarà trasformata interamente in energia potenziale elastica della molla (questa volta in tensione). La velocità della massa m2 nell'istante di separazione dalla massa m1 è sempre v2, per cui la sua energia cinetica è data da:

$K_{2}^{'}=\frac{1}{2}m_{2}v_{2}^{2}$

L'energia potenziale elastica immagazzinata della molla tesa di un tratto ("elongazione") $\Delta x$ ' è:

$U_{e}^{'}=\frac{1}{2}k(\Delta x')^{2}$

Uguagliando le due energie si ottiene:

$\Delta x'=v_{2}\sqrt{\frac{m_{2}}{k}}$

con v2 data dalla (1).

Rispondiamo ora all'ultimo quesito del quiz, quello che chiedeva di determinare il periodo dell'oscillazione della massa m2.

Dopo la separazione della massa m1 , che continua a muoversi verso sinistra, dalla massa m2 connessa alla molla, quest'ultima inizierà ad oscillare attorno alla posizione di equilibrio. Ad essa possiamo applicare la seconda legge di Netwon, che scriviamo in forma differenziale:

$\Sigma F=m_{2}\ddot{x}$ (3)

dove $\ddot{x}$ indica la derivata seconda rispetto al tempo della coordinata x, cioè l'accelerazione. Nel problema in esame basta questa sola coordinata per descriverlo perfettamente poiché le forze hanno componente non nulla solo lungo la direzione delle ascisse (non ci sono attriti e la forza peso è perfettamente bilanciata dalla reazione del piano di appoggio). L'unica forza ad agire in questa fase sulla massa m2 è quella elastica della molla che è data da:

$F_{e}=-kx$

dove il segno meno indica che tale forza, al generico istante di tempo t, si oppone al movimento della massa. Sostituendo questa epressione nella (3) otteniamo:

$m_{2}\ddot{x}+kx=0$ (4)

cioè, dividendo tutto per m:

$\ddot{x}+\frac{k}{m_{2}}x=0$

Questa è una equazione differenziale omogenea a coefficienti costanti. Una soluzione di tale equazione differenziale è:

$x(t)=C_{1}cos\omega t+C_{2}sen\omega t$ (5)

essendo C1 e C2 due costanti da determinare in base alle condizioni iniziali e $\omega$ dato da

$\omega =\sqrt{\frac{k}{m_{2}}}$

Nel nostro caso, all'istante di tempo iniziale t=0 , cioè quando la massa m2 si trova in corrispondenza delle lunghezza a riposto della molla, la coordinata x vale 0 (si pone l'origine esattamente in corrispondenza di questa posizione) e la velocità è v2. La prima condizione (t=0;x=0) fornisce, utilizzando la (5):

C1=0

Per imporre la seconda condizione (t=0; $\dot{x}$ =v2) è necessario trovare l'espressione della derivata prima di x(t) :

$\dot{x}=-C_{1}\omega sen\omega t+C_{2}\omega cos\omega t$

da cui:

$C_{2}=\frac{v_{2}}{\omega }$

In definitiva, la soluzione dell'equazione differenziale, per il caso in esame, é:

$x(t)=\frac{v_{2}}{\omega }sen\omega t$ (6)

con $\omega =\sqrt{\frac{k}{m_{2}}}$

Per convincerci che la (5) è soluzione dell'equazione differenziale basta trovarne la derivata seconda rispetto al tempo, e sostituire questa e la (6) nella (4). Troveremmo un'identità.

La (6) ci dice che il moto della massa m2 è oscillatorio con pulsazione $\omega$ e ampiezza data da $\frac{v_{2}}{\omega }$ . La pulsazione è la velocità con cui viene effettuata una oscillazione completa ed è legata al periodo T, ossia all'intervallo di tempo in cui avviene una oscillazione completa, dalla relazione:

$\omega = \frac{2\pi}{T}$

da cui, dunque, è immediato trovare il periodo cercato:

$T=\frac{2\pi }{\omega }$ cioé, sostituendo l'espressione di $\omega$ e razionalizzando , $T={2\pi }\sqrt{\frac{m_{2}}{k}}$

Quelle seguente è un'animazione del moto oscillatorio della massa m2 dalla separazione con la massa m1 in poi.

Grazie a tutti coloro che hanno proposto le loro risposte ai quesiti del quiz.

L	M	M	G	V	S	D
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Articoli correlati

Due navi in mare aperto (*/**)

Sovrapposizione di stati: non solo gatti **

(Q) Velocità costante **/***

Osservazione della fotosfera del Sole in alta risoluzione

Lascia un commento Cancel Reply

(Q) Velocità costante /*