Questo articolo non riporta solo la soluzione al primo di due recenti quiz, ma vuole descrivere molto di più e, quindi, non perdetevelo! La geometria può diventare una specie di romanzo d'avventura... Potremmo chiamarla "geometria dinamica"!

Ho notato che mentre le derivata è un concetto abbastanza semplice da recepire, ben più difficile è quello di integrale. D'altra parte il "contrario" di qualcosa è spesso più complicato dell'operazione  normale. Ad esempio, pensate alla radice quadrata... Cosa c'entra tutto questo con la corona circolare (e con molti altri problemi)? Il tutto assomiglia a un piccolo giallo, alla portata di chiunque.

La storia è abbastanza divertente e presenta un nuovo piccolo genio. A 17 anni si dovrebbero imparare gli integrali (in Armenia, almeno), ma c'era un ragazzo che probabilmente non li amava e allora ha pensato bene di inventarsi un metodo del tutto visuale, senza inserire alcun calcolo. Come noi sappiamo bene (vero?) gli integrali si usano spesso per calcolare le aree racchiuse da curve che non siano proprio quelle più banali. L'area di una corona circolare non è certo difficile da calcolare e non ha bisogno di integrali, ma ben diverso è il caso di una curva esponenziale, di una cicloide e di molti altri esempi. E così il nostro Mamikon Mnatsakanian, a soli 17 anni, ha introdotto, quasi per caso, quello che viene oggi chiamato "calcolo visuale". Trasferitosi poi negli Stati Uniti, si è laureato ed è stato Professore associato in Astrofisica. Probabilmente ha anche imparato ad amare gli integrali, ma la sua idea geniale (e sicuramente semplice) ha lasciato un segno indelebile, permettendo anche di calcolare aree per le quali ci si trovava di fronte a calcoli quasi insormontabili.

Vi faccio vedere subito in Fig. 1 un esempio sul quale torneremo a tempo debito. Non vi dico nemmeno quali sono le equazioni delle curve descritte, ma sicuramente non sono equazioni da poco e calcolarne l'integrale non è certo  cosa facile (forse impossibile). Eppure per Mamikon diventa uno scherzo...

Prima di passare all'azione in grande stile (la parola "azione" è perfettamente adatta, dato che si tratta di un metodo "dinamico"), torniamo al semplice quiz introduttivo, quello della corona circolare. Disinteressiamoci completamente dei raggi r e R dei due cerchi e concentriamoci sulla corda a. Anzi, tutta la corda è fin troppo... basta considerarne la metà, ad esempio TB.

A questo punto introduciamo la Fig. 2 e mettiamo in moto TB. In che modo? Facciamo muovere T lungo la circonferenza interna, mantenendo però sempre TB come sua tangente. In altre parole, "spazziamo" tutta la corona circolare. Non vi è nemmeno bisogno di parlare di infinitesimi, dato che l'area della corona è data proprio dall'insieme di tutti i segmenti TB dopo che T ha fatto un giro completo.

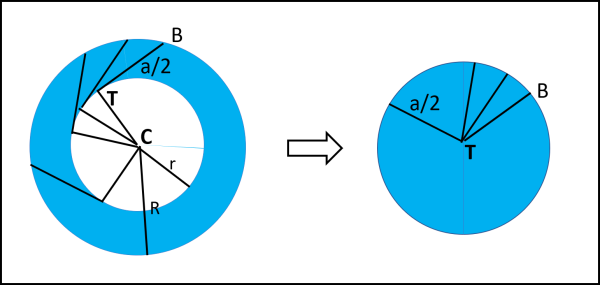
Disegniamo a destra un cerchio in cui al centro fissiamo T e, di conseguenza B si trova a descrivere una circonferenza di raggio TB (che ha  sempre la stessa lunghezza). O, se preferite, riportiamo tutti i segmenti  TB parallelamente a se stessi con T fissato una volta per tutte. In un modo o nell'altro, possiamo dire che l'area della corona circolare è uguale a quella di un cerchio che per raggio proprio la meta della corda a. Da cui si ha:

A_corona = π a²/4

Ma , d'altra parte sappiamo benissimo che l'area di una corona circolare è uguale alla differenza tra l'area del cerchio maggiore meno quella del cerchio minore (questo lo sapeva anche Mamikon...). Ne consegue che:

a²/4 = R² - r²

Il triangolo BTC è però sicuramente rettangolo in T e quindi possiamo dire che il quadrato costruito sui cateti è uguale al quadrato costruito sull'ipotenusa. Una nuova prova del teorema di Pitagora.

Ne segue, ovviamente, che qualsiasi siano i cerchi di partenza, l'area della corona circolare dipende solo dalla corda AB o, meglio ancora, dalla sua semicorda TB. Ovviamente, nel caso in cui il cerchiò più piccolo sia eliminato, la nostra tangente al punto C è proprio il raggio R e non fa che ruotare attorno a C, ossia descrivere  l'area del cerchio più grande. Già di per sé questa splendida soluzione dinamica meritava un dieci e lode, ma Mamikon non si è certo fermato lì... La corona circolare è solo il caso più banale di quello che diventerà il Teorema di Mamikon (con successive elaborazioni). Probabilmente gli alieni che volevano fare i buchi nei pianeti, lo conoscevano bene.

Continuando a elaborare l'idea così geniale di un diciassettenne, essa è risultata una una specie di "uovo di Colombo", tale da farci dire: "Ma come è stato possibile non pensarci prima?". Il nostro amico Fabiopc ci è andato vicinissimo, ma la faccenda è diventata ben più generale, permettendo di risolvere problemi ancora insoluti. Noi ci fermeremo a un certo punto senza andare troppo nel complicato, ma il trovare aree  del tutto impossibili o quasi, senza un'equazione differenziale e/o un integrale, è qualcosa che dobbiamo imparare, almeno nei suoi risultati più chiari e descrivibili facilmente.

Torniamo perciò alla Fig. 1. Due curve veramente assurde, soprattutto quella più in basso. Tuttavia, la loro costruzione è semplicissima, come mostra la Fig. 3.

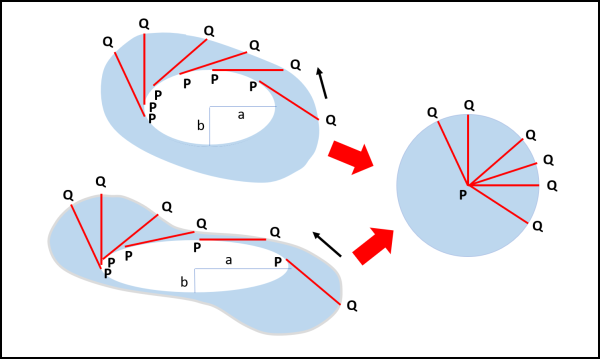
Esse sono state costruite facendo "viaggiare" o - meglio- "spazzare" una certa area alla tangente di lunghezza fissata PQ. In entrambi i casi, però, le aree azzurre si trovano facilmente adottando il procedimento di prima. Basta mettere al centro il punto di tangenza P e far ruotare le tangenti di 360° (ossia trasportare le tangenti nel cerchio di destra parallelamente a se stesse). Entrambe le curve racchiudono la stessa area azzurra. E questo capita qualsiasi sia l'ellisse di partenza! Per conoscere l'area totale delle due strane figure basta aggiungere l'area del cerchio di destra (il cui raggio è sempre uguale alla lunghezza del segmento tangente all'ellisse) all'area delle due ellissi, ben nota a tutti i diciassettenni armeni (πab).

Ma la generalizzazione non è certo finita qui... Andiamo avanti a piccoli passi.

Passiamo, senza problemi, a un triangolo qualsiasi ABC. Sembrerebbe faccenda strana parlare di tangenti, però... però... si può fare come in Fig. 4.

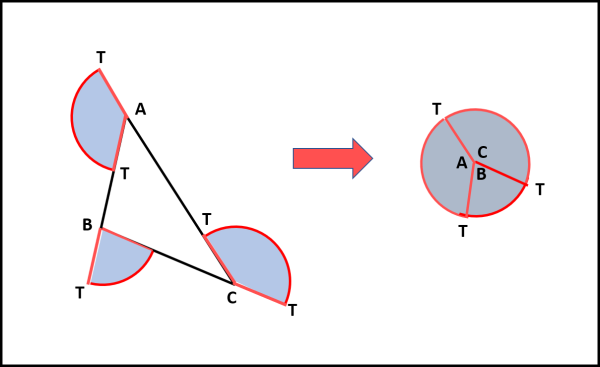
La tangente a un lato rettilineo è il lato stesso. La lunghezza della tangente sia AT. AT inizia a muoversi lungo AB, ma non subisce nessuna rotazione per cui l'area "spazzata" è zero. Quando A arriva in B, la tangente è ancora AT= BT. Poi, però, la tangente deve ruotare per sistemarsi lungo BC. Nel fare questo viene spazzata un'area che è uguale al settore circolare di centro B e raggio AT = BT. Bi si muove lungo BC e la tangente si muove fino ad arrivare a CT. Come prima, in questo tratto, l'area spazzata è zero. Poi, nuova rotazione per sistemarsi in CT lungo CA. Arrivo in A e nuova rotazione per sistemarsi come all'istante iniziale. Una bella azione dinamica, non c'è che dire! Non ci resta che mettere insieme i tre settori di cerchio ed ecco apparire il cerchio di raggio AT=BT=CT e di centro A=B=C.

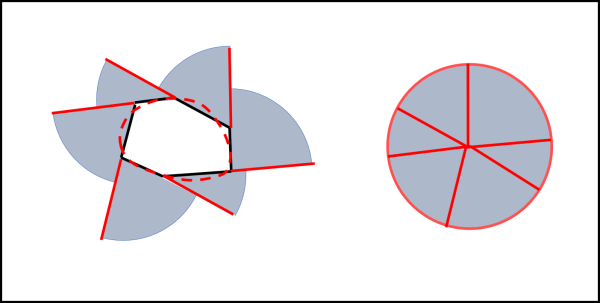
Sembra quasi che sia scherzato, ma non è così... In Fig. 5 consideriamo un poligono qualsiasi e utilizziamo la stessa strategia usata per il triangolo. Nuovamente i vari settori circolari portano a un cerchio di raggio uguale a quello del segmento tangente.

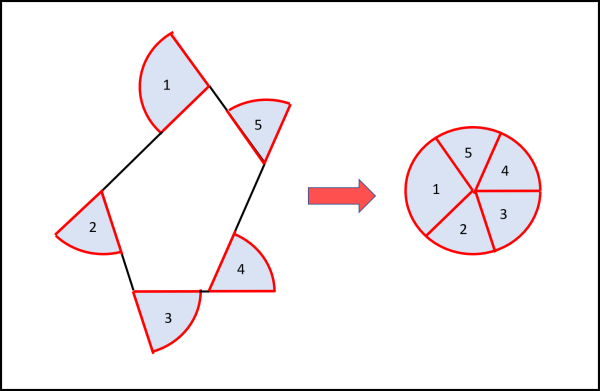
Aumentando il numero di lati si arriverà a una curva continua che deve avere un solo vincolo: essere convessa. La curva che l'ha originata può quindi essere una qualsiasi curva ma l'area spazzata dal segmento tangente rimane sempre uguale al cerchio che ha il segmento come raggio.

A questo punto possiamo scrivere un teorema decisamente generale:

L'area spazzata da un segmento di lunghezza costante, tangente a una qualsiasi curva convessa, è uguale all'area di un cerchio che ha per raggio il segmento tangente.

Ma non è finita ancora... possiamo anche considerare il segmento tangente di lunghezza non costante e ottenere risultati altrettanto semplici e, a volte, veramente unici. Li vedremo nel prossimo articolo insieme alla soluzione del secondo quiz.