Categorie: Matematica
Tags: calcolo visuale Cavalieri cicloide corona circolare Mamikon trattrice
Scritto da: Vincenzo Zappalà
Commenti:0
Il calcolo visuale di Mamikon ***
Questo articolo è stato inserito nella sezione d'archivio "Matematica e Geometria"
Il calcolo visuale di Mamikon è veramente un qualcosa di geniale che stranamente è poco conosciuto. Lo introduciamo utilizzando due semplici problemi di geometria, risolvibili attraverso le semplici formule legate alle aree e ai volumi. Tuttavia, essi possono essere risolti con un metodo del tutto diverso, un metodo che ha permesso di risolvere "a colpo d'occhio" problemi ben più complessi. Come se non bastasse si riesce anche a dimostrare il teorema di Pitagora in un modo del tutto nuovo.
DUE ESERCIZI
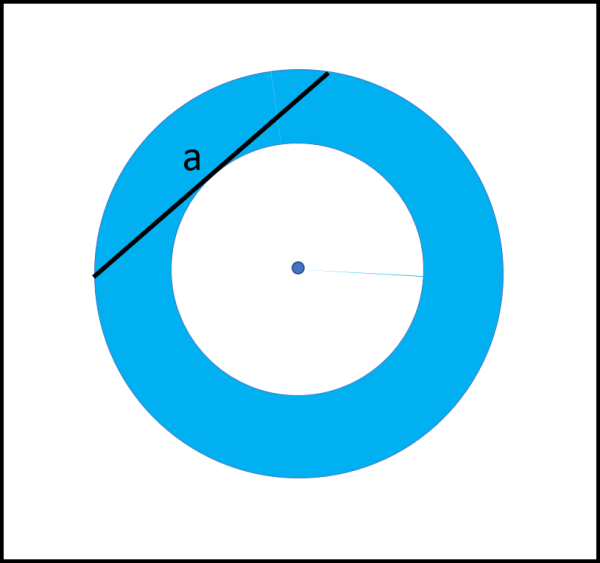
Il primo problema è molto semplice: dati due cerchi concentrici di raggio sconosciuto determinare l'aree della corona circolare definita dai due cerchi conoscendo soltanto la lunghezza della corda di quello più grande tangente a quello più piccolo.
La figura spiega bene la situazione...
Ma la parte più bella è che non si deve usare il teorema di Pitagora, ma -anzi- lo si può ricavare.
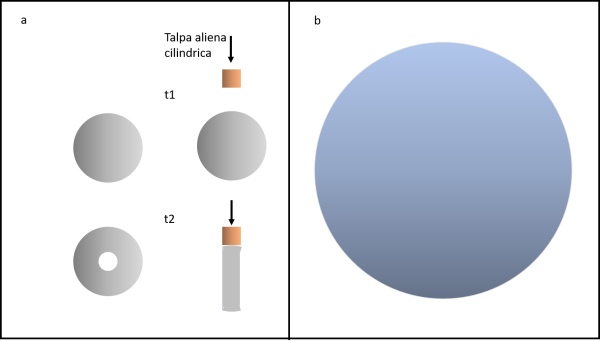
Il secondo problema può essere presentato in modo fantascientifico, pensando a una strana razza aliena che ha la poco piacevole mania di portarsi via enormi "carote" di materia dagli altri pianeti. L'unica cosa che gli alieni rispettano è che ciò che lasciano sul posto deve sempre avere lo stesso volume, qualsiasi siano le dimensioni del pianeta "bersaglio".
Per eseguire lo "scavo", gli alieni usano una "talpa" meccanica a forma di cilindro di raggio variabile capace di estrarre una enorme carota da ogni pianeta che incontra. Sfortunatamente, si è imbattuto nel sistema Terra- Luna e ha deciso di agire su entrambi i corpi celesti (non si cura se sono pianeti o satelliti...). Nella figura che segue vediamo la catastrofica sequela dei fatti...
Nella parte (a) la talpa cilindrica si occupa della Luna. Al tempo t1 si sta avvicinando al bersaglio, mentre al tempo t2 ha già eseguito l'estrazione della carota lunare. A sinistra vediamo la Luna prima dell'operazione (t1) e dopo l'operazione (t2). Della Luna è stato portata via tutta la parte centrale, lasciando solo uno strano anello.
Adesso è il il momento della Terra (parte (b)). Ovviamente, devono cambiare le dimensioni della talpa cilindrica. L'importante è che la parte che rimarrà della Terra dovrà avere lo stesso volume di ciò che è rimasto della Luna.
Ci chiediamo: "Come dovrà essere modificata la talpa affinché si sia sicuri del risultato? E perché ? E quale sarà il valore del volume rimasto, uguale per tutti i pianeti "bucati", in funzione di UNA SOLA variabile?"
Non chiedetemi perché gli alieni hanno questa mania omicida... sono o non sono alieni? Tuttavia, una ragione molto assurda c'è, ma la spiegheremo alla fine...
Ovviamente, anche per risolvere questo secondo problema non vi è assolutamente bisogno di usare integrali. I due problemi, pur sembrando strano, sono strettamente legati tra loro. Anzi, potremmo dire che il secondo è una versione tridimensionale del primo.

PRIMO PROBLEMA E L'INGRESSO DI MAMIKON
Facciamo un po' di storia romanzata...
Per esperienza personale trovo che, mentre le derivata è un concetto abbastanza semplice da recepire, ben più difficile è quello di integrale. D'altra parte il "contrario" di qualcosa è spesso più complicato dell'operazione normale. Ad esempio, pensate alla radice quadrata... Cosa c'entra tutto questo con la corona circolare (e con molti altri problemi)? Il tutto assomiglia a un piccolo giallo, alla portata di chiunque.
La storia è abbastanza divertente e presenta un nuovo piccolo genio. A 17 anni si dovrebbero imparare gli integrali (in Armenia, almeno), ma c'era un ragazzo che probabilmente non li amava e allora ha pensato bene di inventarsi un metodo del tutto visuale, senza inserire alcun calcolo. Come noi sappiamo bene (vero?) gli integrali si usano spesso per calcolare le aree racchiuse da curve che non siano proprio quelle più banali. L'area di una corona circolare non è certo difficile da calcolare e non ha bisogno di integrali, ma ben diverso è il caso di una curva esponenziale, di una cicloide e di molti altri esempi. E così il nostro Mamikon Mnatsakanian, a soli 17 anni, ha introdotto, quasi per caso, quello che viene oggi chiamato "calcolo visuale". Trasferitosi poi negli Stati Uniti, si è laureato ed è stato Professore associato in Astrofisica. Probabilmente ha anche imparato ad amare gli integrali, ma la sua idea geniale (e sicuramente semplice) ha lasciato un segno indelebile, permettendo anche di calcolare aree per le quali ci si trovava di fronte a calcoli quasi insormontabili.
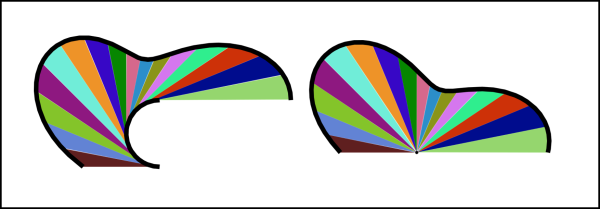
Vi faccio vedere subito in Fig. 1 un esempio sul quale torneremo a tempo debito. Non vi dico nemmeno quali sono le equazioni delle curve descritte, ma sicuramente non sono equazioni da poco e calcolarne l'integrale non è certo cosa facile (forse impossibile). Eppure per Mamikon diventa uno scherzo...

Prima di passare all'azione in grande stile (la parola "azione" è perfettamente adatta, dato che si tratta di un metodo "dinamico"), torniamo al primo facile problema. Disinteressiamoci completamente dei raggi r e R dei due cerchi e concentriamoci sulla corda a. Anzi, tutta la corda è fin troppo... basta considerarne la metà, ad esempio TB.
A questo punto introduciamo la Fig. 2 e mettiamo in moto TB. In che modo? Facciamo muovere T lungo la circonferenza interna, mantenendo però sempre TB come sua tangente. In altre parole, "spazziamo" tutta la corona circolare. Non vi è nemmeno bisogno di parlare di infinitesimi, dato che l'area della corona è data proprio dall'insieme di tutti i segmenti TB dopo che T ha fatto un giro completo.
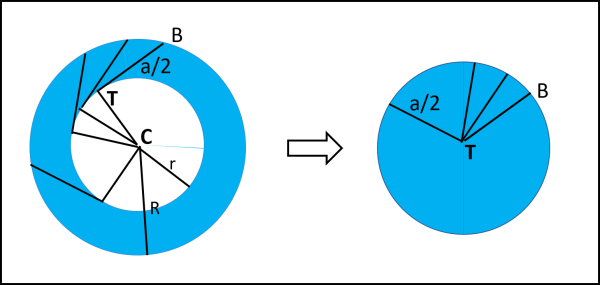
Disegniamo a destra un cerchio in cui al centro fissiamo T e, di conseguenza, B si trova a descrivere una circonferenza di raggio TB (che ha sempre la stessa lunghezza). O, se preferite, riportiamo tutti i segmenti TB parallelamente a se stessi con T fissato una volta per tutte. In un modo o nell'altro, possiamo dire che l'area della corona circolare è uguale a quella di un cerchio che per raggio proprio la meta della corda a. Da cui si ha:
Acorona = π a2/4
Ma , d'altra parte, sappiamo benissimo che l'area di una corona circolare è uguale alla differenza tra l'area del cerchio maggiore meno quella del cerchio minore (questo lo sapeva anche Mamikon...). Ne consegue che:
a2/4 = R2 - r2
Il triangolo BTC è però sicuramente rettangolo in T e quindi possiamo dire che il quadrato costruito sui cateti è uguale al quadrato costruito sull'ipotenusa: una nuova prova del teorema di Pitagora.
Ne segue, ovviamente, che qualsiasi siano i cerchi di partenza, l'area della corona circolare dipende solo dalla corda AB o, meglio ancora, dalla sua semicorda TB. Ovviamente, nel caso in cui il cerchiò più piccolo sia eliminato, la nostra tangente al punto C è proprio il raggio R e non fa che ruotare attorno a C, ossia descrivere l'area del cerchio più grande. Già di per sé questa splendida soluzione dinamica meritava un dieci e lode, ma Mamikon non si è certo fermato lì... La corona circolare è solo il caso più banale di quello che diventerà il Teorema di Mamikon (con successive elaborazioni). Probabilmente gli alieni che volevano fare i buchi nei, lo conoscevano bene.
OLTRE LA CORONA CIRCOLARE
Continuando a elaborare l'idea così geniale di un diciassettenne, essa è risultata una una specie di "uovo di Colombo", tale da farci dire: "Ma come è stato possibile non averci pensato prima?" Noi ci fermeremo a un certo punto senza andare troppo nel complicato, ma il trovare aree del tutto impossibili o quasi, senza un'equazione differenziale e/o un integrale, è qualcosa che dobbiamo imparare, almeno nei suoi risultati più chiari e descrivibili facilmente.
Torniamo perciò alla Fig. 1. Due curve veramente assurde, soprattutto quella più in basso. Tuttavia, la loro costruzione è semplicissima, come mostra la Fig. 3.
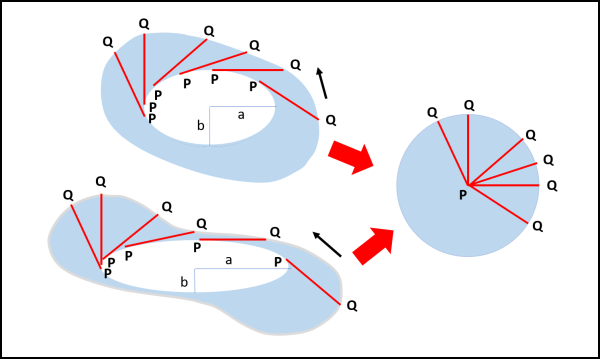
Esse sono state costruite facendo "viaggiare" o - meglio- "spazzare" una certa area alla tangente di lunghezza fissata PQ. In entrambi i casi, però, le aree azzurre si trovano facilmente adottando il procedimento di prima. Basta mettere al centro il punto di tangenza P e far ruotare le tangenti di 360° (ossia trasportare le tangenti nel cerchio di destra parallelamente a se stesse). Entrambe le curve racchiudono la stessa area azzurra. E questo capita qualsiasi sia l'ellisse di partenza! Per conoscere l'area totale delle due strane figure basta aggiungere l'area del cerchio di destra (il cui raggio è sempre uguale alla lunghezza del segmento tangente all'ellisse) all'area delle due ellissi, ben nota a tutti i diciassettenni armeni (πab).
Ma la generalizzazione non è certo finita qui... Andiamo avanti a piccoli passi.
Passiamo, senza problemi, a un triangolo qualsiasi ABC. Sembrerebbe faccenda strana parlare di tangenti, però... però... si può fare come in Fig. 4.
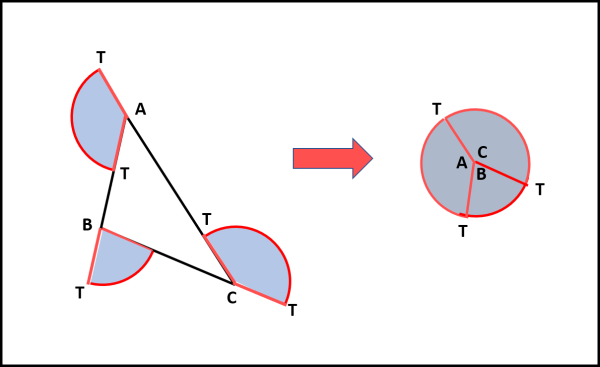
La tangente a un lato rettilineo è il lato stesso. La lunghezza della tangente sia AT. AT inizia a muoversi lungo AB, ma non subisce nessuna rotazione per cui l'area "spazzata" è zero. Quando A arriva in B, la tangente è ancora AT= BT. Poi, però, la tangente deve ruotare per sistemarsi lungo BC. Nel fare questo viene spazzata un'area che è uguale al settore circolare di centro B e raggio AT = BT. B si muove lungo BC e la tangente si muove fino ad arrivare a CT. Come prima, in questo tratto, l'area spazzata è zero. Poi, nuova rotazione per sistemarsi in CT lungo CA. Arrivo in A e nuova rotazione per sistemarsi come all'istante iniziale. Una bella azione dinamica, non c'è che dire! Non ci resta che mettere insieme i tre settori di cerchio ed ecco apparire il cerchio di raggio AT=BT=CT e di centro A=B=C.
Sembra quasi che sia scherzato, ma non è così... In Fig. 5 consideriamo un poligono qualsiasi e utilizziamo la stessa strategia usata per il triangolo. Nuovamente i vari settori circolari portano a un cerchio di raggio uguale a quello del segmento tangente.
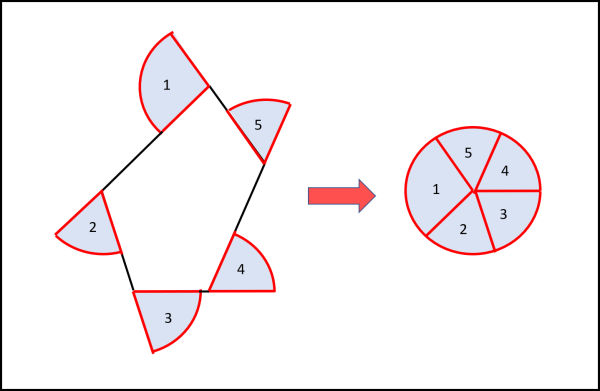
Aumentando il numero di lati si arriverà a una curva continua che deve avere un solo vincolo: essere convessa. La curva che l'ha originata può quindi essere una qualsiasi curva ma l'area spazzata dal segmento tangente rimane sempre uguale al cerchio che ha il segmento come raggio.
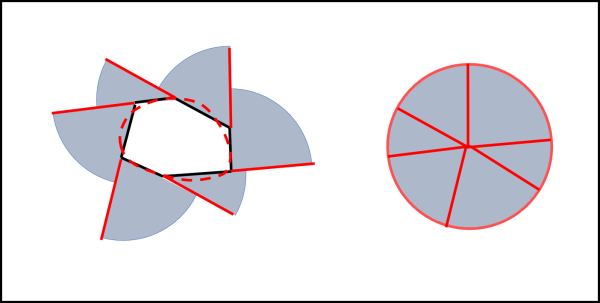
A questo punto possiamo scrivere un teorema decisamente generale:
L'area spazzata da un segmento di lunghezza costante, tangente a una qualsiasi curva convessa, è uguale all'area di un cerchio che ha per raggio il segmento tangente.
Ma non è finita ancora... possiamo anche considerare il segmento tangente di lunghezza non costante e ottenere risultati altrettanto semplici e, a volte, veramente unici.
Diamo una versione ancora più generale del teorema di Mamikon. A prima vista sembrerebbe meno importante, ma in certi calcoli è sicuramente più che utile:
L'area spazzata da un segmento di lunghezza variabile, tangente a una curva qualsiasi, è uguale all'area dell'insieme di tutti segmenti tangenti.
Per comprendere bene il suo significato basta guardare la Fig. 7. A sinistra una curva qualsiasi con segmenti tangenti di lunghezza variabile e a destra l'insieme di tutti i segmenti che abbiano in comune il punto di tangenza. Le due aree colorate sono sempre uguali.
Come già detto, non vogliamo certo affrontare tutte le ricadute del calcolo visuale e quindi torniamo, ancora una volta, alla tangente di lunghezza costante. Questa volta, però, consideriamo una curva molto particolare: la trattrice.
In nome stesso la dice lunga: è una curva che indica il trascinamento e possiamo fare un esempio decisamente terra-terra, ma molto efficace. Una bambina sta trascinando dietro di sé un trenino per mezzo di un filo rigido e, quindi, di lunghezza costante d. Vediamo in Fig. 8 il caso di una bambina che cammini in linea retta (asse x) e che cominci quando il trenino è posto in direzione dell'asse y.
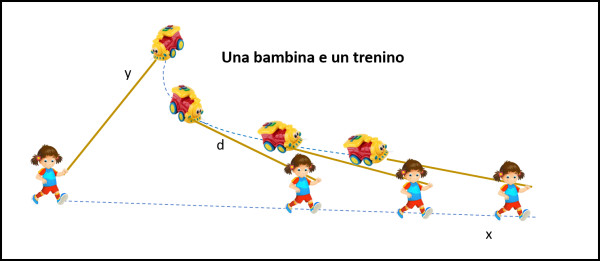
La curva ha una caratteristica molto interessante per noi: durante il movimento della bimba (con velocità costante e infinitesimale) non solo la lunghezza d si mantiene costante, ma il segmento si mantiene tangente alla curva istante per istante. Rappresentiamo la figura precedente in modo più ... rigoroso in Fig. 9.
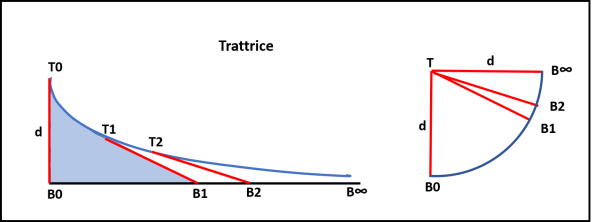
Non ci resta che applicare il teorema di Manikom, facendo coincidere i punti di tangenza nel punto punto T e tracciando tutte le distanze d parallele ai vari segmenti. Otteniamo un settore di cerchio di raggio d con un angolo al centro uguale a 90°. L'area tra la trattrice e l'asse x non è altro che l'area del settore circolare, ossia:
ATR = πd2/4
L'equazione della trattrice non è proprio banale e l'integrale corrispondente altrettanto. Mamikon, però, ha avuto solo bisogno di conoscere l'area di un cerchio. Notiamo anche che si arriva all'infinito senza problemi (l'asse x è l'asintoto orizzontale della curva).
Passiamo ora a una curva molto più conosciuta, l'esponenziale in base e. Sappiamo che questa curva ha una caratteristica estremamente utile: la sua derivata è uguale alla funzione. Al limite il loro rapporto può essere uguale a una costante. E' meglio fare un esempio...
y = ex y' = ex
y = ebx y' = bebx
Prima di passare all'azione diamo un paio di definizioni: (1) sia y = f(x) una certa curva; consideriamo la tangente in suo punto T qualsiasi e prolunghiamola fino a che non intersechi l'asse x nel punto K. Tracciamo da T la perpendicolare all'asse x che lo incontra in H. Il segmento KH viene chiamato sottotangente. (2) Per completezza (anche se a noi interessa poco in questo caso) possiamo anche tracciare la normale alla curva nel punto T (ossia la perpendicolare alla tangente) e prolungarla fino a incontrare l'asse x in N. Il segmento HN viene chiamato sottonormale. Disegniamo il tutto in Fig. 10.
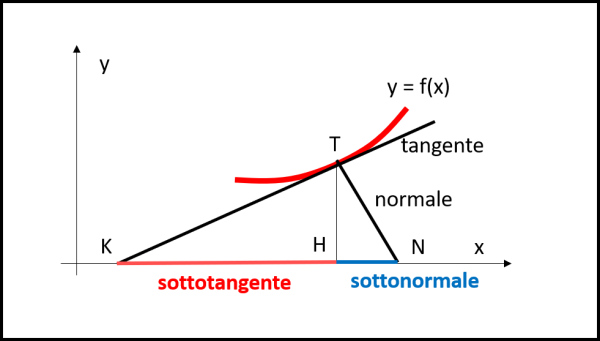
Molto bene. Possiamo adesso disegnare la nostra curva esponenziale di base e con esponente x/a (possiamo sempre ottenere una formula di questo tipo...) e disegniamola in Fig. 11.
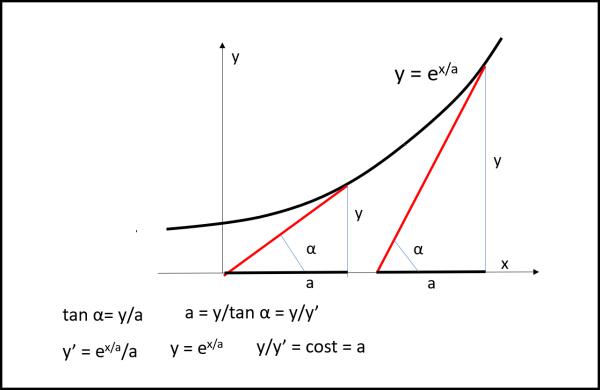
Tracciamo due tangenti (segmenti rossi) qualsiasi e individuiamo le relative sottotangenti. Dobbiamo accettare il fatto che i segmenti tangenti prolungati fino all'asse x non danno certamente segmenti uguali (come capitava per la trattrice), ma, in compenso le sottotangenti sono tutte uguali tra loro. Si dimostra facilmente:
y = ex/a
y' = tan α = (1/a) ex/a
Ma sappiamo anche che:
tan α = y/a (dove a è la sottotangente)
Per cui possiamo scrivere:
y' = y/a
y/y' = a = costante
La sottotangente non cambia mai, qualsiasi sia il punto da cui è stata tracciata la tangente alla curva.
Non ci resta, allora, che far spazzare l'area tra la curva e l'asse x, dal segmento tangente non costante, per ottenere un bellissimo triangolo che ha sempre per base la sottotangente a, come illustrato in Fig. 12.
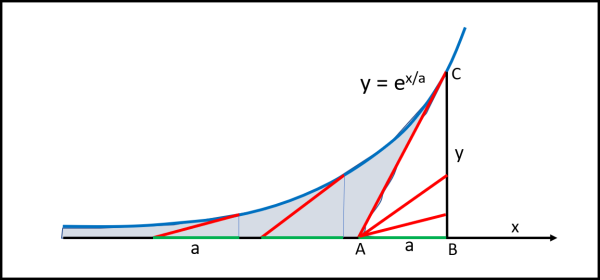
Tracciamo dal punto C che vogliamo la perpendicolare all'asse x e possiamo tranquillamente inserire tutti i triangoli con la sottotangente costante come base. L'area spazzata dalla tangente è proprio l'area del triangolo ACB. Tuttavia l'area del triangolo rappresenta solo l'area della parte colorata in azzurro. Per avere l'area totale fino al segmento CB, basta aggiungere un'altra volta l'area del triangolo ABC. Ne segue che l'area tra la curva e l'asse y è uguale a:
AESP = 2 ay/2 = ay
Ovviamente yC è noto perché corrisponde al valore scelto per xB.
Una piccola grande magia senza alcuna equazione differenziale e nemmeno un integrale. Solo la conoscenza della derivata dell'esponenziale e un minimo di trigonometria spiccia.
Facciamo ancora un passo in più e occupiamoci di una curva che è stata profondamente analizzata in questo Circolo: la cicloide.
Ricordiamo, comunque, come si costruisce. Un cerchio viene fatto rotolare senza strisciare su una retta x. La cicloide è la curva descritta da un qualsiasi punto P della circonferenza. Essa potrebbe essere una curva infinita che continua a ripetersi, ma noi consideriamo solo la parte descritta dal punto P (fissato alla circonferenza) durante una rotazione completa del cerchio. Per semplicità si considera come punto P iniziale (e finale) quello che corrisponde al punto di contatto del cerchio con l'asse x. La vediamo nella Fig. 13.
Essa è una curva che ha tante peculiarità, ampiamente trattate in vari articoli, ma in questo caso siamo interessati all'area compresa tra di lei e l'asse x. Ovviamente, si dovrebbe ricavare la sua equazione e integrarla tra i due punti di contatto. Povero Mamikon! No, no, lui risolve tutto in modo semplice ed elegante.
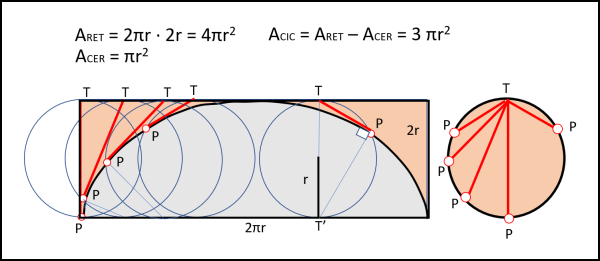
Considera il rettangolo che la contiene e che è tangente al suo massimo. Le dimensioni di tale rettangolo sono ben conosciute: l'altezza è il diametro del cerchio che rotola e la base è la lunghezza della circonferenza. L'area del rettangolo è quindi:
ARET = 2πr · 2r = 4πr2
per trovare l'area azzurra, basterebbe togliere dall'area del rettangolo l'area rosata... E' difficile calcolarla? Nemmeno per sogno! Dobbiamo solo fare un piccolo ragionamento e per far ciò utilizziamo il cerchio più a destra di tutti (ma potrebbe essere uno qualsiasi). I punti T e T' dividono il cerchio a metà, dato che TT' è un suo diametro. Qualsiasi triangolo che abbia TT' come base e il terzo punto P sulla circonferenza deve essere rettangolo, con l'angolo retto in P. Il segmento PT è quindi perpendicolare a T'P. Tuttavia, T' è il punto di rotazione istantanea di P lungo la cicloide e, quindi, PT è anche la tangente alla cicloide nel punto P. Bene, molto bene! Facciamo muovere il segmento TP in modo che spazzi tutta l'area compresa tra la cicloide e il lato superiore del rettangolo. Questi segmenti non sono certo uguali tra loro, ma, per il teorema generale di Mamikon, l'area spazzata da loro deve essere uguale all'area del loro insieme. Per ottenere questo insieme basta fissare un punto T (a destra) e trasportare tutti i segmenti tangenti, parallelamente a se stessi, fino a far coincidere tra loro tutti gli estremi T. Il punto P descriverà una magnifica circonferenza il cui raggio è proprio r. In altre parole, l'area spazzata di colore rosa è esattamente uguale all'area del cerchio che rotola:
ACER = πr2
Ne segue:
ACIC = ARET - ACER = 4πr2 - πr2 = 3πr2
Possiamo concludere, dopo aver solo utilizzato l'area di un rettangolo e quella di un cerchio, che l'area della cicloide (compresa tra la curva e l'asse x) è esattamente tre volte quella del cerchio che rotola! Più semplice di così...
Penso che possa bastare, anche se le applicazioni sono ben più numerose e anche ben più complicate (concettualmente, ma non per i calcoli necessari).
LA TALPA SPAZIALE
Consideriamo le nostre due sfere di raggio diverso. In esse vengono inseriti due cilindri che avranno anch'essi il raggio di base diverso, ma tali che le altezze dei due "anelli" sferici, rimasti intatti, siano uguali. Facciamoci aiutare dalla Fig. 14.
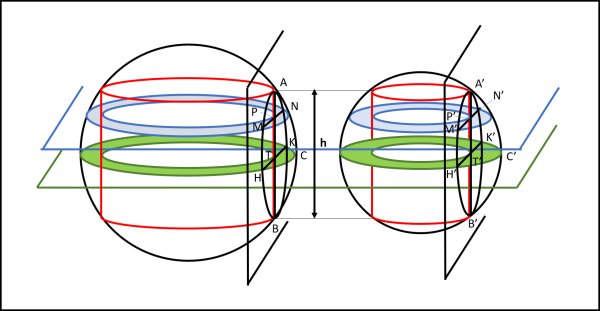
Le due sfere hanno il contorno nero e i cilindri hanno il contorno rosso. Tracciamo un piano perpendicolare all'asse dei cilindri che passi per il cerchio massimo delle sfere (piano con contorno verde). Le sezioni individuano due corone circolari verdi. Come si vede non siamo assolutamente interessati al raggio delle sfera o al raggio delle basi del cilindro: vogliamo solo che AB sia uguale ad A'B', uguali ad h. Prendiamo adesso due piani (neri), perpendicolari al piano precedente che taglino le sfere rimanendo tangenti al cilindro lungo AB e A'B', rispettivamente. Otteniamo due calotte sferiche diverse tra loro. Noi, però, siamo interessati alle circonferenze che i due piani individuano sulle sfere. Queste due circonferenze hanno come diametro AB e A'B', per cui esse sono uguali. in particolare possiamo scrivere che
AB = HK (diametri della circonferenza, tra loro perpendicolari)
A'B' = H'K' (diametri della circonferenza, tra loro perpendicolari)
L'area della prima corona circolare verde viene descritta dalla semicorda tangente al cerchio del cilindro, ossia da HT. L'area della seconda corona circolare verde viene descritta dalla semicorda corrispondente H'T'. Sappiamo, però, che HT = H'T', da cui segue, per il teorema di Mamikon, che esse sono uguali tra loro e hanno la stessa area di un cerchio di raggio AT = A'T' = h/2.
Tracciamo adesso un secondo piano (azzurro) che sia parallelo al piano verde. Anch'esso identificherà due corone circolari azzurre sulle due sfere. Dato che i piani sono paralleli, ne segue che TP = T'P'. Le corde MN e MN', perpendicolari a TP e T'P', rispettivamente, devono essere uguali tra di loro. Possiamo scrivere:
MP = M'P'.
L'area delle due corone circolari azzurre sono nuovamente uguali tra di loro. Possiamo concludere che qualsiasi sia il piano parallelo a quello verde, esso individuerà su entrambe le sfere due corone circolari uguali tra loro, di area uguale a quella di un cerchio di raggio uguale alla semicorda corrispondente a MP.
A questo punto possiamo aggiungere, in Fig. 15, una sfera di raggio h/2.
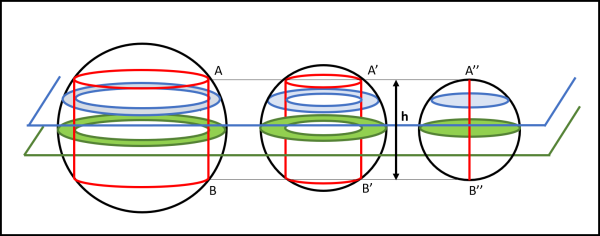
I piani orizzontali paralleli a quello verde individueranno su questa sfera, cerchi di area uguale a quelle delle corone circolari prima descritte. Possiamo perciò dire che le aree determinate da ogni singolo piano sono tutte uguali tra loro. A questo punto basta ricordarsi il Principio di Cavalieri che dice:
Se due solidi hanno uguale altezza e se le sezioni tagliate da piani paralleli alle basi e ugualmente distanti da queste stanno sempre in un dato rapporto, anche i volumi dei solidi staranno in questo rapporto.
Nel nostro caso particolare, l'altezza è pari ad h e le aree stanno nel rapporto 1:1 (ossia sono uguali). Il volume degli anelli sferici rimasti indenni dal passaggio del cilindro deve, perciò, essere uguale a quello di una sfera di diametro h (Fig. 16).
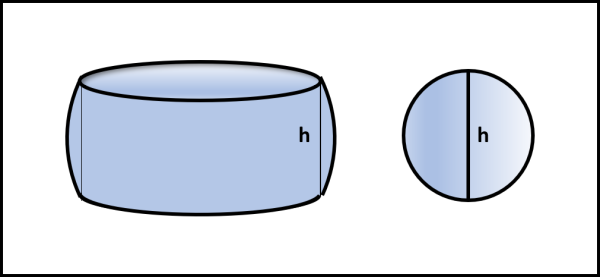
Il volume della sfera è uguale a:
V = (4/3) π h3/8
V = π h3/6
In parole povere, i nostri alieni hanno la mania di ridurre tutti i pianeti ad avere lo stesso raggio, dato che l'autogravitazione fa collassare tutti gli anelli sferici in sfere perfette di raggio h/2.
Boh... gli alieni sono proprio alieni e hanno un senso della democrazia molto particolare (non è che noi si abbia una visione molto più equilibrata)...