Questo articolo è inserito nelle sezioni d'archivio "Matematica e Geometria" e "Meccanica celeste"

In questa prima parte torniamo un po' all'antica... ai bei tempi in cui cercavo di spiegare l'analisi matematica, con tanto di derivate e integrali, in modo comprensibile a tutti coloro dotati di voglia di imparare e di conoscere, per avendo basi di partenza molto basse (che male c'è?). Iniziamo perciò in modo veramente elementare e ci portiamo rapidamente e facilmente a  maneggiare le celebri e bellissime figure di Lissajous. Per far contenti coloro che usano dire: "Sì, belle... ma a che servono?" toccheremo le applicazioni che le hanno portate ad essere fondamentali nel posizionare velivoli spaziali che necessitano di condizioni stabili  e non vicinissime alla Terra. E se ce la sta facendo l'uomo, potete giurarci che non se l'è certo fatto scappare madre Natura!

Rinfrescata elementare

Quando parliamo di funzione, pensiamo subito a un'equazione del tipo:

y = f(x)

In quella "f" ci può essere di tutto e di più... da una costante, a un intreccio diabolico di operazioni matematiche. Tuttavia, il senso finale è presto detto: "Facciamo variare la x come cavolo ci pare (sempre nei suoi limiti che possono essere ristretti o infiniti), ma  la "f" ci permette di costringere la y a muoversi secondo regole ben precise". E' un po' come se portassimo un cane al guinzaglio... noi andiamo dove vogliamo e il cane è costretto a seguirci!

Vi è quindi un legame ben stretto tra le due variabili che siamo soliti inserire in un diagramma con assi tra loro perpendicolari che chiamiamo assi cartesiani. Se ne fissiamo una, l'altra è obbligata a seguire la regola che gli impone la funzione "f".

In realtà, però, nessuno mi vieterebbe di rendere del tutto indipendenti i due valori di x e y (lasciare libero il cane). In poche parole, posso sempre scegliere un'ascissa x qualsiasi e associarle una y altrettanto qualsiasi e presa a caso. Beh... non avrei fatto altro che indicare la posizione di un punto P del piano. In questo modo, un po' alla volta, evitando le ripetizioni, descriverei tutti i punti del piano (il tutti è da prendere con le molle, dato che esistono infiniti punti in un piano e rimangono infiniti anche in una piccolissima parte di piano, per cui è meglio dire, ad esempio, che possiamo segnare tutti i punti che hanno ascissa e ordinata intere in un certa parte di piano).

Nulla toglie, quindi, che x e y vivano la loro vita in modo del tutto indipendente e non abbiano nessun legame a priori e nessun vincolo reciproco. Ognuna può scegliere la strada che preferisce. Appena, però, introduciamo quella "f"  tra x e y, ecco che scatta un legame indissolubile che può essere sia banale che estremamente complicato e coinvolgere -magari- potenze, radici quadrate, logaritmi, formule trigonometriche e molte altre operazioni tra le più ricercate in ambito matematico.

Perché sto ripetendo cose che sapete sicuramente tutti benissimo? Perché vorrei introdurre nuovamente le equazioni parametriche (anche queste ben note) per poi veder come alcune di queste possono non solo mostrarci figure bellissime e quasi poetiche (non per niente sono collegate al mondo della musica), ma anche indispensabili per le strategie dei telescopi spaziali che cercano disperatamente di consumare poca energia e di parcheggiare  in totale sicurezza o quasi.

Riprendiamo, quindi, le equazioni parametriche di una funzione e rendiamoci conto della loro essenza e della loro utilità.

Cosa vuol dire "parametriche"? In parole molto semplici far credere al signor "x" e al signor "y" di essere del tutto indipendenti tra loro, ma legarli invece entrambi a un terzo parametro, che, giocando di nascosto, ne vincola gli spostamenti. In altre parole, sia il signor x che il signor y si muovono seguendo una certa legge che dipende dal come si presenta il parametro t.

Facciamo il caso più classico, quello più squisitamente "fisico". La parte del parametro "nascosto" la diamo al tempo t. Se non entriamo nella relatività, siamo sicuri che sia il signor x che il signor y hanno orologi che lo misurano nello stesso identico modo.

Il signor x decide di fare una bella passeggiata lungo il suo asse. Sappiamo che può andare sia lentamente che a spasso svelto, pur mantenendo un ritmo costante. In parole un po' più serie e stringate possiamo dire che la velocità di x è costante. Ne segue che la sua relazione con il tempo è data da:

x = v t         (dove v è un costante e indica quanto spazio il signor x percorre nell'unità di tempo). Addirittura, se prendessimo come unità di misura il metro e il secondo, x potrebbe decidere di camminare proprio alla velocità di un metro al secondo e l'equazione precedente diventerebbe:

x = t

Guarda caso anche il signor y ha deciso di fare una passeggiata lungo il suo asse e decide di andare alla stessa velocità del signor x. Ne segue:

y = t

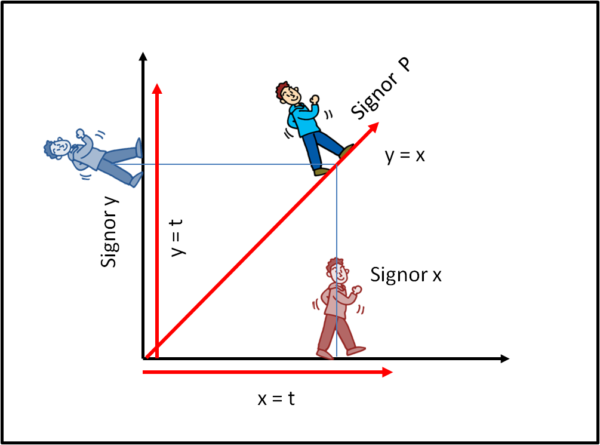
Il piano è formato, però, da infiniti punti e non solo da quelli che stanno lungo l'asse x o l'asse y (anche loro infiniti, comunque). Prendiamo allora il signor P che ha voglia di attraversare il piano, seguendo un percorso del tutto particolare: seguire pari pari i movimenti dei due signori precedenti. Senza rendersene conto (oppure sì, dipende) il suo movimento crea un legame tra la sua x e la sua y (ricordiamo che qualsiasi signor P è sempre identificato da una x e da una y... come se fosse tenuto sotto controllo da qualche strana App... si dice così?). Beh... possiamo allora facilmente scrivere le equazioni parametriche che lo identificano nella sua passeggiata:

x_P = t

y_P = t

In modo sicuramente banale e scherzoso abbiamo scritto le equazioni parametriche (c'è di mezzo il parametro tempo) della passeggiata di P.

Le due equazioni mi dicono che le due coordinate sono sempre uguali a t e allora posso tranquillamente eliminare t e scrivere:

y = x

ossia ritorno immediatamente all'equazione canonica di una retta passante per l'origine e inclinata di 45° rispetto agli assi. In realtà, tanto il punto P si muove secondo l'asse x e tanto si muove secondo l'asse y.

Dov'è finita la funzione "f"? C'è, c'è... ma vale solo e soltanto UNO, ossia mi dice prendi x, non fargli assolutamente niente, e otterrai  la y.

Le passeggiate le vediamo rappresentate in Fig. 1

Ovviamente, le equazioni parametriche, ossia le passeggiate di x e di y possono anche svolgersi a velocità diverse. Se P volesse imitarli dovrebbe seguire regole un po' più artcolate...

Ad esempio, x si muova con una velocità di 2 metri al secondo:

x = 2t

mentre y si muova ancora più velocemente

y = 3t

Come si deve muovere P, se vuole seguire questi due movimenti ?

Beh... prima di tutto dobbiamo mettere in evidenza la t in entrambe le equazioni parametriche:

t =x/2

t = y/3

e poi uguagliare...

y/3 = x/2

y = (3/2) x

Abbiamo di nuovo ottenuto una semi retta che passa per l'origine (se x = 0, anche y = 0), ma è più inclinata rispetto all'asse x.

Generalizziamo ancora di più i movimenti del signor x e del signor y. Ad esempio, possono partire entrambi (o uno soltanto) da posizioni non coincidenti con l'origine O. Ad esempio x parte dalla posizione x₀ = 1 , ossia, al tempo zero, prima di iniziare la passeggiata, si trova già lungo la strada che percorrerà in seguito e lo stesso può fare il signor y (ad esempio parte da y₀ = 2).

Le due passeggiate si scrivono allora

x = 1 + 2t

y = 2 + 3t

Eliminando come al solito il parametro indipendente t:

2t = x - 1

3t = y - 2

t = x/2 - 1/2

t = y/3 - 2/3

y/3 - 2/3 = x/2 - 1/2

y/3 = x/2 + 2/3 - 1/2 = x/2 - (4 - 3)/6 = x/2 -1/6

y = (3/2)x - 3/6 = 3/2x - 1/2

Che è l'equazione generica di una semiretta che non parte dell'origine. Prolungando tutte queste passeggiate, ricaviamo tutte le rette possibili, cambiando le costanti velocità e punto di partenza. Ricordiamo, tra parentesi, che la velocità non è altro che la tangente dell'angolo formato dalla retta con l'asse del signor x.

Possiamo, perciò, dire che le equazioni parametriche di una retta qualsiasi sono del tipo:

x = at + b                     .... 1a

y = ct + d                     .... 1b

che portano alla forma canonica, del tipo y = f(x), in modo molto semplice, eliminando il parametro t:

t = (x - b)/a

t = (y - d)/c

(y - d)/c = (x - b)/a

ay - ad =  xc - bc

y = (c/a)x + (ad - bc)/a

Che è proprio la classica equazione della retta

y = f(x) = mx + n

dato che a, b, c e d sono costanti come lo sono m e n.

Non sto a proseguire in questi termini veramente elementari, ma si capisce subito che il signor x potrebbe camminare accelerando e quindi cambiare la velocità  istante per istante. Il signor y potrebbe, invece, mantenere un passo cadenzato... Alla fine troveremmo un andamento curvilineo di P che altri non è che una parabola, così come succede nel moto del proiettile.

Ma gli esempi sarebbero infiniti...

Fino a questo punto abbiamo considerati legami tra i signori x  e y con il parametro t che seguano andamenti rettilinei, a velocità costanti oppure con accelerazione costante (caso della parabola, ad esempio).

Qualcuno potrebbe dire: "Sì, interessante... ma perché non usare subito la forma classica della curva o di quello che viene fuori?" Beh... può capitare che mentre le due equazioni parametriche sono di facile analisi, lo stesso non capiti eliminando la t tra di loro. La  "f" che ne deriva può essere veramente una bestia dura!

Va bene... finita la parte ultra didattica (che  avranno sicuramente saltato tutti i nostri lettori abituali) passiamo a costruire equazioni parametriche leggermente più complicate, ma sempre a un livello comprensibile da tutti.

Passeggiate un po' diverse

Spesso e volentieri le equazioni parametriche utilizzano come parametro "t" un qualcosa di puramente geometrico, come, ad esempio, un angolo. Quando ci sono di mezzo gli angoli finiamo quasi obbligatoriamente nelle funzioni trigonometriche, soprattutto seno e coseno. Detto in parole più tecniche, possiamo cambiare il legame che esiste tra i signori x e y e il parametro t, facendolo diventare, ad esempio, un moto ripetitivo e periodico (proprio come quello scandito da un seno o da un coseno). Un classico esempio è il moto oscillatorio, quello ci un pendolo, di un'onda luminosa, di un'onda acustica, ecc.

Immaginiamo, allora che il nostro signor x abbia deciso di fare una strana passeggiata: parte dal punto O e arriva fino a un certo punto R che dista "a" dall'origine; poi torna indietro e magari prosegue dalla parte opposta rispetto fino a S, posto a una distanza "a" uguale a quella dell'andata (ossia OR); infine torna indietro. Il tutto lo fa in modo continuo , ripetitivo e ... periodico. Ossia impiega sempre lo stesso tempo a partire , tornare in O, proseguire dall'altra parte e tornare ad O e a ripetere l'intera passeggiata. Il mondo migliore per esprime questo strano moto è quello di associarlo a una funzione periodica e l'ideale è proprio utilizzare una funzione trigonometrica come, ad esempio, il seno di un certo angolo. Scriviamo, ad esempio:

x = a sen α

Il parametro che comanda il tutto è questa volta l'angolo α. Quando x parte, l'angolo è zero e x si trova nell'origine (il seno di zero è zero).Il punto più lontano della sua camminata  viene raggiunto quando l'angolo è 90°, ossia quando il seno vale 1 e x si viene a trovare alla distanza a dall'origine. Poi l'angolo supera 90° e il signor x torna indietro in quanto il seno diminuisce. A 180°, x è tornato al punto di partenza. Continuando a far crescere l'angolo, esso diventa maggiore di 180° e il suo seno diventa negativo. Perfetto! proprio quello che vuole il signor x che si muove verso  valori negativi allontanandosi di nuovo dall'origine. A 270°, x raggiunge nuovamente la distanza a , ma con segno meno (il seno di 270° vale - 1). Infine torna indietro al punto O quando α vale 360°, ossia il seno ha compiuto il suo periodo e può ricominciare da capo. In Fig. 2 vediamo la passeggiata del signor x e il legame tra come essa si svolge e il seno di un angolo che ruota di 360° in modo uniforme. Salta già all'occhio che il parametro α, pur variando in modo uniforme, ossia con una velocità angolare costante, causa un movimento del signor x assolutamente non uniforme. Il signor x è costretto a seguire la variazione dell'angolo attraverso la trasformazione che ne fa il seno. In altre parole, l'angolo ruota come la lancetta di un orologio, ma lo spazio percorso dal signor x è costretto a non essere eseguito  a velocità costante.

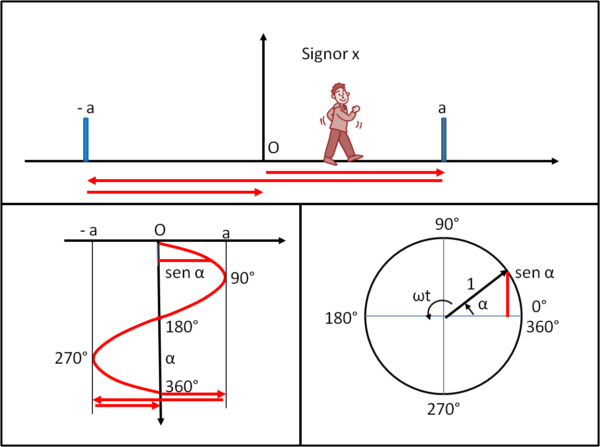
Conviene allora rendere più chiaro questo andamento introducendo nuovamente il parametro t (il solito tempo) ed esprimendo l'angolo in altro modo. Intanto ribadiamo il concetto appena espresso (come sempre è meglio abbondare)

Cosa avevamo fatto per la passeggiata a velocità uniforme? avevamo considerato costante la velocità lineare. Ossia avevamo detto che il signor x continuava a fare sempre lo stesso numero di metri nello stesso numero di secondi. Bene, questa volta non è più così. Infatti, il signor x  inizia con una certa velocità lineare, ma rallenta sempre più andando verso "a", fino a fermarsi. Poi torna indietro sveltendo sempre più il passo per raggiungere la massima velocità lineare in O. Poi rallenta nuovamente fino a fermarsi appena giunto in "-a" e infine aumenta nuovamente il passo per tornare in O. Possiamo dire, questa volta, che non è il tragitto lineare compiuto che è sempre lo stesso nell'unità di tempo, durante il percorso, ma è l'angolo, che comanda il valore del  seno, che varia dello stesso numero di gradi per intervalli uguali di tempo. Abbiamo semplicemente introdotto la velocità angolare ω (gradi al secondo) e l'abbiamo considerata costante.

La funzione seno, però, ha bisogno di un angolo... Poco male, sappiamo, infatti, che la velocità angolare è un angolo per l'unità di tempo... basta allora moltiplicate la velocità angolare per il tempo e avere proprio l'angolo. In linguaggio matematico elementare:

ω = gradi/secondi

t = secondi

ωt = gradi  x secondi/secondi = gradi

Al posto dell'angolo α possiamo perciò scrivere ωt . ω è una costante per definizione e, quindi, il tempo torna ad essere il parametro fondamentale . Una puntualizzazione molto importante: noi stiamo trattando t come il parametro tempo e ω come un angolo che gira. In realtà essi sono parametri che matematicamente possono essere qualsiasi cosa. In pratica, però, ossia in fisica, il tempo è un parametro che deve comunque comparire in qualche modo (almeno nei fenomeni del macrocosmo) e accettiamolo per quello che è: un vero prepotente; ma come faremmo senza di lui? Tutti fermi, immobili, con o senza... mascherine! Un perfetto lockdown (ma chiamarla chiusura? no... troppo poco "moderno").

Scriviamo perciò il movimento di x come:

x = a sin α = a sin ωt            .... (2a)

Immaginiamo che il signor y che abbia deciso di fare la stessa cosa, con la stessa velocità angolare. Avremmo:

y = a sin α =  a sin ωt                 .... (2b)

Beh... il secondo membro è uguale per entrambi i camminatori e quindi ne deriva un moto  "combinato"

y = x

ossia la solita retta che passa per l'origine e inclinata di 45°.

Aver utilizzato le equazioni parametriche (2), per questo caso, non sembra certo essere stato particolarmente utile, dato che abbiamo ottenuto la stessa traiettoria geometrica, ossia la retta. Tuttavia, il moto su di essa non è più il moto a velocità costante rappresentata dalla (1). L'equazione finale è la stessa, ma le equazioni parametriche (1) e (2) spiegano anche che tipo di moto viene eseguito dal signor P lungo la stessa traiettoria geometrica. In qualche modo, scrivere y = x è una rappresentazione puramente geometrica, mentre scrivere le (1) o le (2) è una rappresentazione fisica.

Prendiamo, ora, una caso leggermente diverso...

Curve a volontà

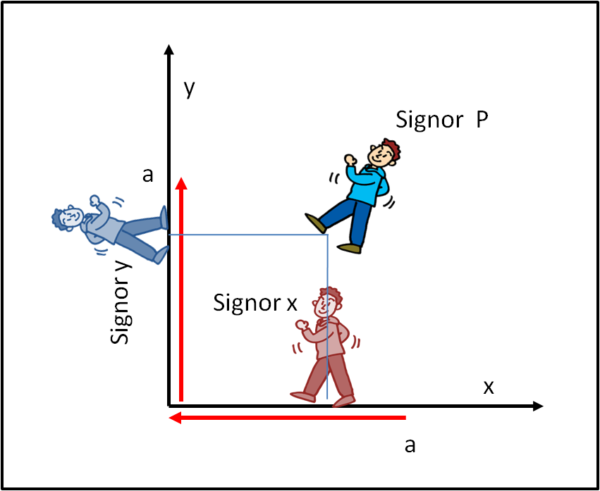
Il signor y decide di  seguire ciò che dice la (2b), mentre il signor x decide di partire dal punto di massima distanza dall'origine, ossia dove x = a. Come possiamo rappresentare  le loro equazioni parametriche? facile... sfasando l'angolo di 90°.

x = a sin (ωt + 90°)

y = a sin ωt

Cosa succede in pratica? Beh... al tempo t = 0, x comincia a muoversi da "a"  verso l'origine, mentre y si muove dall'origine verso il suo valore y = a. Quando x arriva in O, y è arrivato in "a". Poi x prosegue verso valori negativi e quando giunge in "- a", y è tornato nuovamente a zero. Poi x torna indietro e y si allontana verso valori negativi, fino a "- a". Infine, y torna indietro al valore 0, mentre x torna la punto iniziale "a". I due moti sono rimasti inalterati, ma sfasati tra loro. Cosa succederebbe al signor P che volesse muoversi concordemente con x e y...  Troviamolo in modo "matematico"

x = a sin (ωt + 90°) = a cos ωt  (ricordiamo che cos α = sen (90° + α))

y = a sin ωt

Quadrando e sommando abbiamo:

x² + y² = a² cos² ωt + a² sen² ωt  = a² (cos² ωt + sen² ωt ) = a²      

x² + y² = a²

Accidenti! Il signor P si muove lungo la circonferenza di raggio a, con centro nell'origine: lui non tocca mai il centro, ma sta sempre alla massima distanza "a" girandogli attorno, come mostra la Fig. 3.

Bene, non abbiamo fatto altro che scrivere le usatissime equazioni parametriche della circonferenza...

In questo caso, però, il moto fisico del signor P è ben diverso da quello di x e di y. Mentre loro viaggiano a velocità lineare sempre diversa da punto a punto, il signor P descrive la circonferenza  non solo a velocità angolare costante, ma anche a velocità lineare costante! Sappiamo bene che se ci si muove di moto circolare uniforme resta costante, in modulo, anche la velocità tangenziale.

Nel frattempo, abbiamo imparato una cosa molto importante anche se ovvia: possiamo utilizzare tranquillamente il seno per entrambe le equazioni (sfasandole di 90°) oppure usare il seno e il coseno. Ah.. che simpatiche le funzioni trigonometriche!

E se ci fossero due coefficienti a e b diversi?

Proviamo:

x = a sin (ωt + 90°)

y = b sin (ωt)

x/a = sin (ωt + 90°) = cos (ωt)

y/b = sin (ωt)

quadrando e sommando:

x²/a² + y²/b² = cos²(ωt) + sin²(ωt) = 1

E "voilà" la ben nota equazione dell'ellisse  di semiassi a e b:

x²/a² + y²/b² = 1

Si potrebbero fare decine e decine di casi, ma limitiamoci a generalizzare quanto abbiamo ricavato facendo passeggiare i nostri signori x e y e, di conseguenza, anche il signor P.

x = a sen (ω_xt + θ)               .... 2a

y = b sin (ω_yt) .... 2b

Attenzione: ω_x, ω_y  sono sempre delle costanti, durante tutto il moto, ma sono diverse tra di loro (sono delle velocità...), così come θ può essere un angolo qualsiasi. Provate, adesso a eliminare la t e a vedere che curva viene fuori... No, non è più così facile! Notiamo che parlare di velocità angolari diverse, vuol dire essere più o meno rapidi nel compiere il giro completo, ossia più o meno rapidi a compiere un periodo. Stiamo perciò parlando anche di frequenza. a e b sono , invece, costanti che moltiplicano le funzioni trigonometriche e quindi causano una variazione della loro ampiezza. θ è un angolo qualsiasi e, quindi, sfasa completamente le due funzioni e non esiste un facile legame tra di loro. Insomma, si capisce bene che in questo modo si può ottenere di tutto e di più.

Queste sono le equazioni parametriche di una moltitudine di curve sia chiuse che aperte, alcune dalla forma veramente affascinante. Il parametro indipendente è sempre t , con l'aggiunta di 5 costanti che possiamo scegliere a piacere. Come già detto, stiamo parlando di moti oscillatori, in cui entrano in ballo le frequenze e le ampiezze. Ne segue che possono essere applicate non solo ai movimenti su è giù per una retta, ma anche a qualsiasi fenomeno fisico oscillatorio. Non per niente le figure si ottengono molto spesso attraverso fasci luminosi o attraverso sovrapposizione di suoni.

Bene, siamo in grado di introdurre tranquillamente le curve di Lissajous, divertirci un po' con altri casi particolari, complicandole anche e applicandole all'astronautica (qualitativamente, ve lo prometto!), ricordando che la Natura le segue senza alcun problema. Basta avvicinarsi al moto dei tre corpi, anche quello più semplificato.

continua...