Categorie: Curiosità
Tags: diagonali geometria lati quadrilateri quattro punti quiz segmenti
Scritto da: Vincenzo Zappalà
Commenti:8
Quattro punti cercano casa * (con risposta)
Vi ho propinato i tensori e, allora, inseriamo anche un quiz molto semplice che abbisogna solo di un po' di riflessione, senza formule o equazioni o funzioni trigonometriche. Insomma un problemino per qualsiasi livello...
Quattro punti (A,B,C,D) cercano casa... ma la cercano proprio speciale! Innanzitutto deve stare tutta su un piano e due punti non possono stare nello stesso posto. A questo punto ci vuole poco a dedurre che esistono sei e solo sei segmenti che uniscono tra loro i quattro punti a due a due. Bene, questi quattro amici vogliono che questi segmenti abbiano solo due lunghezze ammissibili. Come già detto la lunghezza uguale a ZERO non è accettata (due punti sovrapposti).
Vi chiedo di descrivere e -se potete- disegnare tutte le possibili case per i nostri quattro amici. Ovviamente i casi di rotazione o di riflessione della stessa casa non valgono...
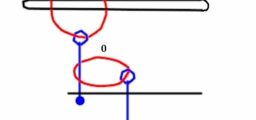
Qui di seguito una casa che non va affatto bene!
Vi prego... diamo una casa ai nostri quattro amici!
P.S.: volevo prendere come esempio il nostro caro amico Franco Travaglino. Per colpa mia (che non ho mai scritto un vero articolo sulle formule trigonometriche meno utilizzate) ha faticato un po' per risolvere il quiz su Gigi Riva. Ma, alla fine, ce l'ha fatta e penso che si sia anche divertito. Non tolgo ancora il quiz su Giggiriva proprio per lui, perché, se ha tempo, cercherà di risolverlo anche senza trigonometria. Grazie Franco!
Magari imitatelo!
SOLUZIONE
La soluzione la trovate nel commento di Fabrizio... le case adatte ai nostri quattro punti sono solo SEI. Si potrebbe anche dimostrare che non possono esisterne altre, ma sarebbe un lavoraccio che vi condono!






8 commenti
A me sono venute in mente solo due possibili case per i quattro punti... mi sembra strano che non ce ne siano altre
ce ne sono... ce ne sono..
grazie Scherzy per aver dato il buon esempio!!!
Vado al volo con lo smartphobe, non posso allegare immagini.
3 punti disposti ai vertici di un triangolo equilatero, il quarto punto disposto nel baricentro del triangolo equilatero. Abbiamo due misure, una per i tre lati del triangolo e una per la distanza del quarto punto dai 3 vertici del triangolo.
e siamo a tre... ne mancano ancora tre!
Eccone un'altra:
approfitto per inserire qui la figura della mia prima risposta al quiz:
ottimo Artù !!
Ho cercato di trovare un metodo, in gran parte empirico, per orientarmi.
Parto dal fatto che i 4 punti sono identici tra loro poiché ognuno è connesso a tutti gli altri. Quindi le differenze le fanno le assegnazioni dei due tipi di lunghezze.
Esamino come esempio il caso di 4 di un tipo e 2 dell'altro tipo. Per l'allocazione dei 2 del secondo tipo alle distanze tra i punti credo ci siano solo due possibilità:
Fatto questo la scelta degli altri 4 è vincolata:
Al primo caso sono riuscito ad abbinargli un'unica soluzione.
Per il secondo ci possono essere due varianti.
Il caso di 3 di un tipo e 3 dell'altro ci sono 3 possibilità:
Nelle figure con 4 punti non è possibile che non abbiano estremi in comune.
Anche in questi casi la scelta degli altri 3 è vincolata:
Quindi alla fine ci sono due possibilità poichè la prima e la terza formano una stessa figura, cambia solo la denominazione del tipo.
Di queste non ho trovato altre varianti.
Nel caso di una di un tipo e 5 dell'altro c'è solo una possibilità. La figura che corrisponde è quella del rombo formata da due triangoli equilateri contrapposti
ottimo come sempre... e si potrebbe anche dimostrare che non ne possono esistere altri... ma è un lavoraccio matematico che vorrei evitare. State pronti che tra non molto arriva il quiz per voi "ultra esperti"!!!