Questo articolo è stato inserito nelle sezioni d'archivio"Relatività Generale" e  "Matematica e Geometria"

Ebbene sì... proviamo finalmente a definire in modo molto semplificato (spero) il fantomatico "tensore" che tanta paura esercita in chi cerca di avvicinarlo. Lo facciamo in modo forse meno convenzionale, cercando di affrontarlo da un punto quasi puramente geometrico, sperando che i due asterischi diano la giusta quantificazione della sua effettiva difficoltà (ossia è articolo per TUTTI coloro che si sentano di dare del tu ai vettori). Pensiamo che sarà poi più semplice capirne le proprietà che lo rendono anche un "oggetto" di pura matematica. Inoltre, cerchiamo anche di approfittare di questa introduzione per capire ancora meglio sia l'importanza e la genialità concettuale della Relatività Generale, sia la difficoltà estrema che si cela dietro una formula finale dall'apparenza molto innocua.

Il nostro compagno, in questo viaggio verso la definizione e la comprensione del tensore, è un punto o poco più. Lo trattiamo come un piccolo cubetto di materia, ingrandendolo e rimpicciolendolo a seconda dei nostri interessi specifici.

Inseriamolo, innanzitutto, in uno spazio a tre dimensioni euclideo, quello in cui siamo un po' tutti convinti di vivere. Il salto verso le quattro dimensioni lo accenneremo alla fine, ma per i tensori ha poca importanza. Questa frase dovrebbe già eliminare molti dubbi: un tensore ha un interesse limitato per le dimensioni dello spazio in cui opera: lo stesso tipo di tensore può vivere in due, tre, quattro dimensioni... ma il suo RANGO (o ORDINE o GRADO) non cambia. Avremo tempo in seguito per approfondire la questione.

Il nostro spazio viene normalmente definito dalle tre coordinate cartesiane x, y e z e anche adesso utilizziamo questa rappresentazione (Fig. 1).

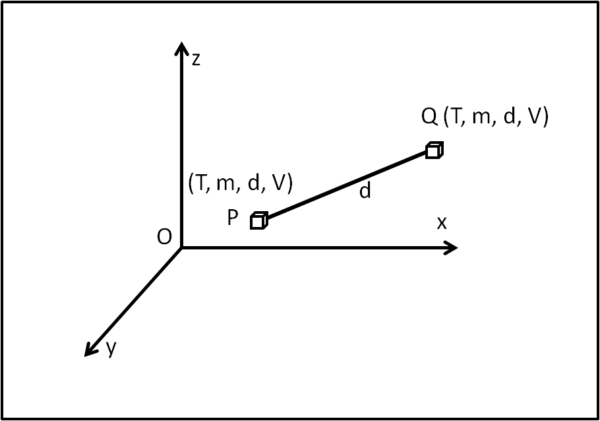
Che sia punto o un cubetto, vicino a lui possiamo scrivere molte caratteristiche che lo definiscono in modo sempre più approfondito. Ad esempio, il nostro punto-cubetto ha una sua massa m, ha anche una certa temperatura T(essendo così piccolo, possiamo considerare la sua temperatura unica), si trova a una certa distanza da un altro punto Q che abita lo stesso spazio, ha un certo volume, e molte altre ancora. In ogni modo, queste caratteristiche sono esprimibili solo con dei "numeri". Basta, infatti, un numero e un'unita di misura per definirle completamente. Questi numeri li chiamiamo SCALARI. Le operazioni che si possono fare su di loro sono quelle che ci insegna l'algebra.

Immaginiamo, adesso, che il nostro punto-cubetto voglia spostarsi fino a raggiungere Q. Sì, magari conosciamo già qual è la distanza in metri tra loro due, ma per farlo spostare abbiamo anche bisogno di definire una direzione e un verso. In altre parole non basta dire a P che Q si trova a un certa distanza in metri, il punto P deve conoscere anche la direzione  che lo congiunge a Q e deve anche muoversi da P verso Q.

Non basta più un numero, uno scalare, per descrivere lo spostamento s di P, ma è necessario introdurre un nuovo "operatore" che contenga informazioni sulla distanza da percorrere, sulla direzione da prendere e sul verso da usare. Introduciamo così il VETTORE, una vera e propria "freccia", la cui lunghezza corrisponde allo scalare distanza, ma che dà informazioni anche sulla direzione, e la cui "punta" indichi il verso. Insomma un vero e proprio tomtom delle automobili!

Abbiamo già studiato e discusso delle operazioni che si possono compiere sui vettori (QUI) e non abbiamo bisogno di tornarci sopra. Sappiamo anche -e soprattutto- che la nostra freccia rimarrebbe quella che è in qualsiasi sistema di riferimento scegliessimo (ossia potremmo spostare l'origine degli assi x,y e z, ma anche ruotarli e molto altro ancora), ma il vettore che indica lo spostamento rimarrebbe uguale. O, almeno, rimarrebbe uguale il suo modulo, ossia lo scalare che ne definisce la lunghezza. Ma non rimarrebbero uguali le sue tre componenti rispetto agli assi cartesiani scelti. Eppure noi abbiamo bisogno delle sue componenti per poter descrivere in modo perfetto lo spostamento  nel sistema che abbiamo scelto.

Inciso facoltativo:

Facciamo un classico esempio di vettore: la velocità (che poi altro non è che lo spostamento nell'unità di tempo). Essa è rappresentata da un bel vettore che viene associato al punto-cubetto P. Essa ha un certo modulo v che rimane, ad esempio, costante. Tuttavia, questo vettore di modulo costante, pur rimanendo sempre lo stesso, acquista un significato ben diverso da un punto di vista sia geometrico che fisico se, ad esempio, continua a cambiare direzione e verso.

Se continuassimo, ad ogni suo cambio di direzione, a cambiare gli assi di riferimento lo vedremmo sempre costante sia in modulo che in direzione e verso (sistema di riferimento solidale con il punto P), ma se il vettore venisse sempre osservato in un solo sistema di riferimento, il suo cambiamento di direzione diventerebbe fondamentale per capire che cosa stia facendo il punto-cubetto P rispetto a un osservatore esterno (sistema di riferimento esterno). In questo secondo caso il nostro punto P descriverebbe, ad esempio, una circonferenza attorno a un punto centrale (magari proprio l'origine degli assi), ossia descriverebbe un moto circolare uniforme che ci porterebbe subito a pensare che su di lui stia agendo anche un'accelerazione e quindi una forza. Nel primo caso, invece potremmo ammettere che il punto si muova di moto rettilineo uniforme senza subire nessuna accelerazione, anche se -stranamente- si sente spinto sempre verso l'esterno.

Non vorrei avere creato confusione invece di chiarezza, ma ho soltanto descritto i due modi di vedere il moto circolare uniforme  causato da una forza centripeta, come, ad esempio, la forza di gravità newtoniana. Lo scopo di questo approfondimento è solo quello di far comprendere molto bene come le condizioni del nostro vettore rispetto a un certo sistema di riferimento siano essenziali non solo per definire compiutamente la freccia, ma anche per definire un certo fenomeno fisico.

Le componenti non sono altro che la completa rappresentazione della freccia nel sistema di riferimento. Dobbiamo, perciò, definirle molto bene a costo di sembrare fin troppo precisi e fiscali...

Come fare a introdurre delle componenti che diano tutte le informazioni sullo spostamento di P fino a Q, proprio nel sistema prescelto? Il modo migliore (e non "sbuffate", dato che la sua importanza la vedremo bene più avanti) è quello di introdurre dei particolari vettori che agiscono solo sui tre assi cartesiani. Stiamo parlando dei VERSORI (ricordate?), non altro che vettori di modulo unitario che possono muoversi ognuno lungo un solo asse cartesiano. Quello dell'asse x l'abbiamo chiamato i, quello dell'asse y, j e quello dell'asse z, k. Cosa dobbiamo fare, allora, con il nostro vettore s spostamento (abbiamo fatto coincidere l'origine degli assi con P per semplicità visiva, tanto non cambia niente)? Proiettarlo sui tre assi e vedere  quante volte i versori  corrispondenti vengono contenuti  in queste proiezioni. Fatemi scrivere una semplicissima formula che conosciamo tutti molto bene:

s = s_x i + s_y j + s_z k

Questa è la vera carta d'identità del nostro vettore s. Esso viene definito come somma di tre vettori (componenti) che viaggiano ognuno secondo un singolo asse cartesiano. Il primo vettore (s_xi) è un vettore che ha come modulo (parte scalare, ossia s_x) il numero di volte che il versore unitario i è contenuto nella proiezione del vettore s sull'asse x, e che ha la direzione e il verso del versore i. La direzione è quella che è, identica a quella di i; il verso si può facilmente indicare con il segno posto davanti al modulo: se esso è positivo il vettore "componente" è concorde con il verso di i, se è negativo il verso è quello opposto. La stessa cosa vale per gli altri due assi. Una volta stabilite queste componenti è facilissimo costruire la somma vettoriale con la regola del parallelogramma o con il metodo che si preferisce (Fig. 2).

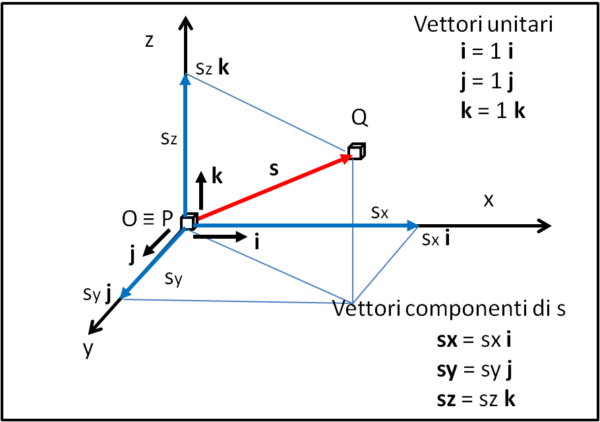
Solo a questo punto, possiamo permetterci di toglierci dai piedi quei rompiscatole dei versori e trattare solo con le componenti scalari dei tre vettori componenti. Infatti, adesso, sappiamo molto bene che operazioni abbiamo fatto per definire lo scalare (ossia il numero) s_x. La sua apparenza di essere solo un numero nasconde il contributo essenziale dato dai versori, che possiamo anche chiamare vettori base per comodità e uniformità nel prosieguo della trattazione.

Il nostro vettore s può quindi venire rappresentato con tre soli numeri, messi, ad esempio, uno sopra l'altro e chiusi eventualmente dentro due parentesi rotonde, ossia dandogli la forma di una matrice, ma poco importa in questa trattazione chiamare questo insieme di numeri con un nome matematico. A noi basta sapere che questi tre numeri indicano perfettamente e completamente il nostro vettore.

s_x

s_y

s_z

Facciamo solo un  piccolo accenno matematico che ci servirà quanto prima. Quanti vettori base abbiamo considerato? Tre, proprio come le dimensioni del nostro spazio. Quante componenti sono state associate ai nostri vettori base? Beh... una e una sola, una per i, ossia s_x; una per j, ossia s_y e una per k, ossia s_z. Riassumendo tre basi e una componente per base. Una componente per base vuole anche dire un solo indice (o pedice nel nostro caso), ossia quella piccola x o y o z che abbiamo associato a ogni componente scalare.  Questo nel caso del vettore.

Torniamo al caso iniziale, quello dello scalare, tipo temperatura o massa. Quanti vettori base abbiamo considerato? Beh... non ne abbiamo usato  nessuno. Il che vuol dire che non abbiamo nemmeno avuto bisogno di utilizzare degli indici dato che è bastato scrivere un numero per ottenere l'informazione completa su quello scalare: T o m o d o quello che volete era più che sufficiente. Fatemi allora scrivere questa definizione molto particolare, ma estremamente indicativa:

In uno spazio a n dimensioni, un tensore di rango r è un oggetto matematico che ha r indici e n^r componenti 

Accidenti siamo già arrivati ai tensori senza averne ancora parlato? Ebbene sì, dato che ne abbiamo già introdotti DUE, lo scalare e il vettore!

Scriviamo la definizione per il nostro scalare:

In uno spazio a 3 dimensioni, un tensore di rango 0 è un oggetto matematico che ha zero indici (perfetto!) e  3⁰ = 1 componenti (esatto!).

Lo scalare diventa perciò un TENSORE di rango 0.

Scriviamola per il nostro vettore spostamento:

In uno spazio a 3 dimensioni, un tensore di rango 1 è un oggetto matematico che ha 1 indice (la x, o la y, o la z) e 3¹ = 3 componenti.

Un vettore diventa un TENSORE di rango 1.

A questo punto potrei anche terminare l'articolo, perché per avere un tensore superiore basta aumentare il numero di componenti... Sto, ovviamente scherzando, dato che il bello comincia adesso. Torniamo però a una visione fisica del nostro punto-cubetto e vediamo come fare degli esempi ancora più chiari del nostro tensore di grado 1, ossia del nostro vettore.

Il  punto P viene immerso non solo nello spazio a tre dimensioni, ma è costretto a subire l'azione di una forza, ad esempio la forza di gravità G (ma potrebbe essere qualsiasi altra forza). Stiamo ancora parlando in termini newtoniani, ovviamente (Fig. 3).

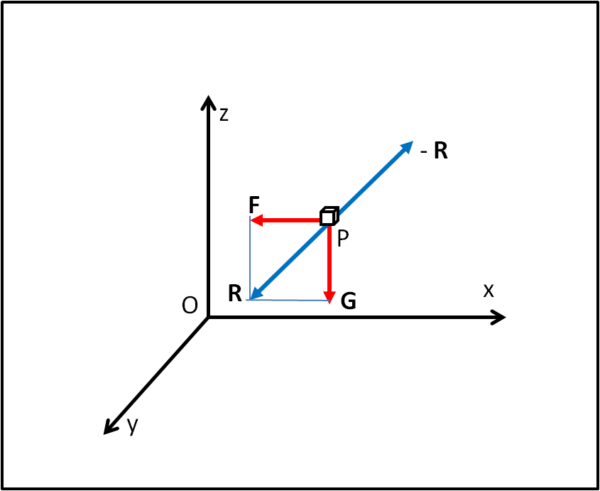
Bene, sappiamo come fare: applichiamo la forza nel centro di massa del nostro punto-cubetto e associamogli un vettore che rappresenti la forza di gravità. Dopo di che il tutto diventa un problema cinematico e dinamico che sappiamo trattare in molti modi.

Complichiamoci un po' la vita... mentre il punto P cade verso il basso (asse z) trascinato dall'accelerazione causata dalla forza, la quale accelerazione determina la velocità di P e infine il suo spostamento  (tutti vettori, ovviamente), cerchiamo di metterlo in salvo dandogli una spinta laterale, magari lungo la direzione dell'asse x. In poche parole, inseriamo una nuova forza F che si aggiunge a quella di gravità G. Beh... la faccenda è ancora piuttosto semplice... basta infatti applicare la forza F nel centro di massa è fare la somma delle due forze, ottenendo una forza risultante R che comanda la nuova accelerazione di P, la sua velocità e il suo spostamento.

A questo punto possiamo aggiungere tutte le forze che vogliamo, ma il problema non cambia concettualmente e poco ci importa se dobbiamo sommare n forze, tutte applicate nel centro di massa del "povero" cubetto-punto P.  Magari, alla fine, a furia di applicare forze a destra, a sinistra, sopra e sotto, riusciremo anche a fare stare immobile il nostro amico P, immobile rispetto al sistema di riferimento che abbiamo considerato, ovviamente. Ad esempio applicando nella Fig. 3 un forza - R uguale e contraria a R. Finalmente, abbiamo regalato l'equilibrio a P.

Abbiamo avuto bisogno di qualcosa di più dei tensori di rango 1, ossia dei vettori? Assolutamente no! Il nostro problema è rimasto comunque confinato nelle tre dimensioni. Di grande aiuto è stata la possibilità di portare tutte le forze nel centro di massa e poi poterle sommare tranquillamente. Eravamo interessati al movimento di P è abbiamo ottenuto tutte le informazioni a riguardo. In altre parole, abbiamo potuto tranquillamente sommare le forze dato che ci interessava solo l'effetto che esse avevano sullo spostamento del punto P.

Pur rimanendo in ambito newtoniano, possiamo però vedere la faccenda in un contesto più generale. In realtà, il nostro cubetto-punto è stato immerso non solo nello spazio, ma anche in un campo gravitazionale, dato che in ogni posizione che assumeva al passare del tempo subiva una forza di gravità corrispondente. Anche la forza che cercava di opporsi poteva far parte di una campo di forza. In poche parole, il nostro cubetto P poteva continuare a essere considerato un punto, che si portava appresso i suoi scalari come massa, temperatura e così via .

Passiamo adesso a un'altra situazione, leggermente più complicata che farà sorridere tutti gli ingegneri civili che ci leggono: il nostro cubetto - punto lo prendiamo all'interno di un oggetto solido (come esempio più comune). L'intero corpo solido subisce gli effetti delle forze esterne, tipo la gravità, ecc., ma i suoi cubetti- punti interni subiscono anche delle forze che nascono proprio dai cubetti vicini, ossia da tutto ciò che circonda il nostro singolo cubetto. Stiamo parlando dello "stress" che subisce il materiale. Pensate a quanto sia importante stabilirlo quando P è all'interno di un ponte o una struttura solida in genere. Attenzione, però... i tensori non si applicano solo allo studio dei materiali "edili", ma anche all'elettromagnetismo, alla meccanica dei fluidi e, come vedremo, a tutto lo spaziotempo curvo.

Ogni punto P deve rimanere in equilibrio sotto l'azione delle forze che su di lui agiscono da parte del materiale che lo circonda, più o meno ingigantite o create da movimenti del terreno o da altri fattori esterni. A noi, comunque, interessa solo il contributo finale che arriva al nostro cubetto-punto. Non voglio nemmeno parlare del ponte di Genova, ma pensiamo a un terremoto. Lui è un evento esterno che però causa delle deformazioni all'interno di una struttura solida che a loro volta agiscono in modo diverso su ogni singolo cubetto-punto interno. Il terremoto dà luogo a uno stress che potrebbe rompere l'equilibrio del cubetto P. Se non è stato già tenuto in conto in anticipo (case antisismiche), questo stress improvviso può far crollare tutto (si veda, per esempio, l'effetto del vento sui ponti sospesi, di cui abbiamo parlato QUI). Gli ingegneri (civili, soprattutto) mi perdonino la grande semplificazione...

Ci torneremo sopra, ma pensiamo solo un attimo a un cubetto immerso in un campo capace di creargli uno stress di questo tipo solo per effetto di una deformazione dell'intero spazio che lo circonda. La faccenda non è poi tanto diversa, ma ci apre le porte verso la Relatività Generale.

Vediamo allora cosa succede al punto P, che a questo punto possiamo far diventare veramente un cubetto a tutti gli effetti con le sue facce ortogonali tra loro. Immergiamolo nello spazio a tre dimensioni e nel campo di stress che lo circonda completamente.

Senza andare troppo nei particolari tecnici (basta studiare Scienze delle Costruzioni per avere un'idea ben più generale e completa) assumiamo che lo stress subito dal cubetto tenda a espanderlo da ogni parte. Il cubetto si sente dilatare e ha bisogno di una rappresentazione molto accurata di ogni forza-vettore che agisce su di lui. Non è più sufficiente applicare le varie forze nel centro di massa del cubetto, dato che vogliamo proprio sapere come queste forze tendano a deformare il cubetto in questione.

Siamo costretti a considerare tre facce del cubetto, scelte, ad esempio e per comodità, proprio perpendicolari ai tre assi del sistema di riferimento spaziale. Come possiamo identificare queste tre facce? Beh... proprio in base al vettore base che le rappresenta. La faccia perpendicolare all'asse x viene individuata dal vettore base i, quella perpendicolare all'asse y dal vettore base j e quella perpendicolare all'asse z dal vettore base k. Ognuna delle tre facce ha quindi un indice già assegnato, ossia x, y e z.

Ogni faccia ha, comunque, i suoi tre assi cartesiani sempre paralleli ai corrispondenti assi delle altre facce e paralleli a quelli dello spazio esterno(immaginate se cambiassimo l'orientamento degli assi o la scelta delle facce... o se prendessimo assi non cartesiani, magari curvilinei... ehm... ehm...), come mostrato in Fig. 4 (non spaventatevi della figura, basta seguire la trattazione passo dopo passo), dove abbiamo usato colori diversi per identificare gli assi cartesiani relativi a ogni singola faccia. Le facce sono state colorate con lo stesso colore e chiamate faccia x, faccia y e faccia z.

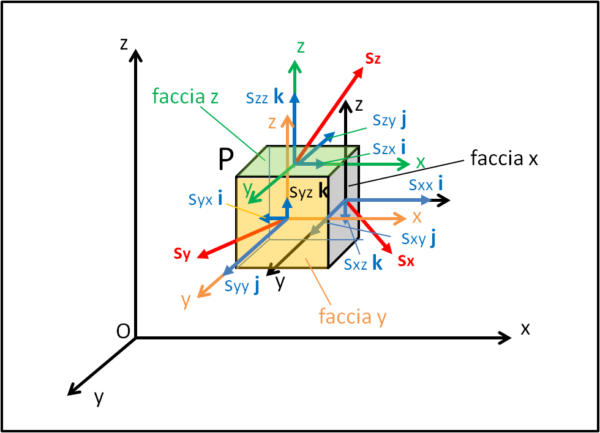
Per affrontare il caso più generale possibile, ipotizziamo che ogni faccia subisca uno stress diverso, anche se è più che plausibile una qualche uguaglianza, come ad esempio che lo stress abbia lo stesso modulo anche se direzioni diverse.

Consideriamo adesso la forza di stress s_x (fatemela chiamare così) che colpisce solo la faccia perpendicolare a x. Essa cerca di spostarsi verso l'esterno e può facilmente (è un vettore) essere identificata dalle sue tre componenti lungo x, y e z, ossia per mezzo dei vettori base i, j e k.

Ricapitoliamo un attimo: abbiamo scelto una faccia che viene identificata da un vettore base e per la forza agente su questa faccia vengono considerate le tre componenti secondo i tre vettori base. In poche parole siamo di nuovo nel caso in cui avevamo rappresentato il vettore, con l'aggiunta però che ad ogni faccia viene associato anche l'indice che la contraddistingue. Sulla faccia perpendicolare a x introduciamo le tre componenti relative alla forza che agisce su questa faccia. Non ci basta più, però, chiamare s_x, s_y e s_z queste tre componenti, ma abbiamo bisogno di identificare anche la faccia. Beh... basta scrivere le componenti in questo modo

s_xx

s_xy

s_xz

Che vogliono dire (scusate la ripetizione): sulla faccia x individuiamo, sui tre assi x,y e z, le componenti della forza che agisce su di lei. Il primo indice ci indica la faccia, il secondo la componente della forza.

E abbiamo "piazzato" la faccia  di indice x (ossia quella perpendicolare all'asse x).

La stessa cosa, però, dobbiamo farla con le altre due facce... Su quella y (perpendicolare all'asse y) dobbiamo descrivere le tre componenti della forza di stress che agisce sulla quella faccia: una secondo l'asse x, una secondo l'asse y e una secondo l'asse z. Come fatto prima otteniamo un secondo vettore con le sue tre componenti, in cui si deve aggiungere l'indice y relativo alla faccia che stiamo considerando:

s_yx

s_yy

s_yz

Un attimo, un attimo... prima di andare avanti perché non sommiamo subito le componenti che sono dirette nella stessa direzione, come s_xx e s_yx ? Perché faremmo un errore... Queste componenti agiscono in modo ben diverso sul cubetto. La componente s_xx tende a trascinare verso l'esterno il cubetto e in particolare la faccia x (forza normale); la componente s_yx tende, invece, a spostare tutta la faccia  o - ancora meglio-  a farla ruotare attorno all'asse z. Insomma è come se volessimo sommare pere con mele. Se vogliamo mantenere tutte le informazioni sulle deformazioni del cubetto dobbiamo lasciarle separate!

Ne consegue che per definire completamente la situazione  delle forze agenti sul cubetto abbiamo bisogno non più di solo tre componenti come nel caso del classico vettore, ma di ben nove componenti. Infatti, come fatto per x e y, dobbiamo definire le componenti s_zx, s_zy e s_zz che sono relative alla faccia z (perpendicolare all'asse z). Ricapitolando, abbiamo bisogno di nove componenti di cui tre sono "normali" e 6 sono "di taglio".

Qualcuno potrebbe dirmi... "un attimo, un attimo... hai fatto tanto il pignolo sul tipo di componente e poi ti sei fermato a tre facce, quando tutti sappiamo bene che il cubetto ha sei facce!" La mia risposta sarebbe semplice: "Stiamo cercando l'equilibrio del cubetto e, come conseguenza, il contributo delle altre tre facce deve essere uguale e opposto a quello delle tre facce considerate. Solo così si ottiene l'equilibrio statico!

Un'altra considerazione potrebbe essere quella relativa all'effettiva esistenza di tutte e nove le componenti. Se la forza agente sulla faccia x avesse una direzione perpendicolare alla faccia, esisterebbe solo la componente s_xx, mentre le altre due (s_xy e s_xz) andrebbero a zero. idem per le altre facce. Questa constatazione è più che giusta, ma ciò non toglierebbe niente al nostro operatore (tensore) che avrebbe comunque nove componenti anche se solo tre  diverse da zero. Un caso particolare e nulla più. Inoltre le tre componenti rimaste avrebbero comunque bisogno dei due indici, dato che è ben diverso dire s_x e s_xx. La seconda scrittura dice molto di più della prima, in quanto non solo ci dice la direzione della componente, ma quale tipo di forza è stata applicata per ottenerla (solo normale e non di taglio).

Scriviamo finalmente il nostro tensore:

s_xx    s_yx    s_zx

s_xy    s_yy    s_zy

s_xz    s_yz     s_zz

Applichiamogli la definizione

In uno spazio a n dimensioni, un tensore di rango r è un oggetto matematico che ha r indici e n^r componenti 

In uno spazio a 3 dimensioni, un tensore di rango 2 è un oggetto matematico che ha 2 indici e 3² = 9 componenti.

Perfetto, è proprio lui! Abbiamo costruito un tensore vero e proprio, un tensore di rango 2.

Se aumentassimo le dimensioni dello spazio, cosa cambierebbe? Beh... cambierebbe il numero di componenti, in quanto il numero di facce dovrebbe essere quattro (come le dimensioni), ma non cambierebbe  il numero degli indici necessari a definire le componenti delle singole facce.

Il tensore avrebbe la forma (la quarta dimensione l'abbiamo considerata t, così ... a caso):

s_xx   s_yx   s_zx    s_tx

s_xy   s_yy   s_zy    s_ty

s_xz   s_yz    s_zz    s_tz

s_xt   s_yt     s_zt    s_tt

Il numero delle componenti salirebbe a 16, come nel caso del vettore che da tre sarebbe salito a 4. Tuttavia il rango del tensore rimarrebbe 2.

Per far crescere il rango del tensore si dovrebbe aumentare il numero degli indici, cosa che diventa molto più astratta e puramente matematica. Possiamo fermarci al rango 2...

Nota Bene: Questa è stata una trattazione quasi puramente geometrica, il cui scopo era quello di arrivare sempre più vicini alla comprensione dell'enorme complessità dell'equazione di Einstein per la Relatività Generale. Abbiamo utilizzato un  esempio legato allo studio dei materiali, in cui gli ingegneri civili la saprebbero certamente più lunga. Oltretutto, vi sono molte convenzioni su come descrivere la matrice finale. Ad esempio, si può notare che le componenti "di taglio" si eliminano l'una con l'altra in casi di uguale dilatazione (o contrazione) su ogni faccia. Si ritorna a una matrice (rappresentazione di tutte le componenti) che ha diverse da zero solo le componenti ortogonali (normali) alle facce, ossia quelle che stanno lungo la diagonale del nostro insieme di componenti. Ma le cose sono ancora più complicate sicuramente e io ne ho dato una versione molto "leggera", sufficiente (spero), però, per giungere allo scopo che ci eravamo prefissati: spiegare in parole semplici cos'è un tensore e comprendere la sua utilità in campo astronomico, ossia nella RG. Ricordiamo, infatti, che i tensori sono fondamentali anche in elettromagnetismo e in altri campi della fisica.

Nella definizione che abbiamo scelto per definire il tensore, manca però un pezzo fondamentale che fa dei tensori uno strumento eccezionale. Riportiamola completa...

In uno spazio a n dimensioni, un tensore di rango r è un oggetto matematico che ha r indici , n^r componenti e che segue delle particolari regole di trasformazione.

Bene queste particolari regole di trasformazione ci conducono a una ulteriore proprietà fondamentale dei tensori in genere (e non solo dei vettori e degli scalari, che in fondo sono anch'essi dei tensori).

Il tensore è invariante rispetto al cambiamento di coordinate.

Ma, in modo ancora più forte: il tensore è tale che le sue componenti sono prevedibili  quando si attua un cambiamento di sistema di riferimento.

Tutto ciò è sicuramente fondamentale per la fisica classica e per lo studio dei materiali, ma lo è anche quando si scala verso lo spazio di Minkowski a 4 dimensioni . Tuttavia, Minkowski può lavorare ancora con un vettore e non con un tensore di rango superiore a 1. Egli lavora, però, su 4 dimensioni, accettando un forte legame tra spazio e tempo, dettato dalla Relatività Ristretta,  su un spazio "piano", quasi euclideo. Il suo infatti è un quadrivettore, ossia un vettore a quattro dimensioni (e ciò porta anche all'invariante spaziotemporale). Non possiamo tacere, però, che tutto il suo spaziotempo potrebbe essere rappresentato da un tensore (ogni "faccia" del suo cubetto subisce quattro componenti e si giunge a una matrice 4 x 4), anche se molto particolare, avendo diverse da zero solo le componenti lungo la diagonale della matrice. Ma fermiamoci qui...

Forse basta solo questo per capire la complessità dell'equazione fondamentale della RG. Il cubetto viene immerso in un campo di forze simile a quello dello stress, ma che dipende dalla presenza di una massa dominante. In altre parole è tutto lo spaziotempo che si deforma e costringe il nostro cubetto a subire altrettante deformazioni e a muoversi secondo "strade" obbligatorie. Esso diventa proprio il mollusco di cui abbiamo parlato all'inizio. Ricordiamo la celebre sintesi perfetta data da J. Wheeler:

La materia dice allo spaziotempo come incurvarsi, e lo spazio curvo dice alla materia come muoversi 

L'apparenza semplice, quindi, non è altro che un insieme mostruoso di complicatissime equazioni che lo stesso Einstein aveva giudicato non essere risolvibili se non attraverso notevoli approssimazioni. Un guazzabuglio di tensori e di trasformazioni che si spogliava della sua natura essenzialmente e puramente matematica e che diventava il linguaggio migliore per descrivere l'Universo! Proprio qui sta la grandezza insuperata (per adesso) di Einstein, aver cioè saputo sfruttare un linguaggio di pura matematica per parlare in un linguaggio fisico del tutto nuovo, che è poi quello del Cosmo.

Riportiamo un "pezzo" delle Conclusioni dell'articolo sulla Relatività Generale:

Le leggi che governano la relatività generale sono, in pratica, due:

(1) Il cambiamento della geometria dello spaziotempo a causa della presenza di una massa. Esso  viene espresso come “eccesso” di raggio di curvatura, in funzione della massa, all’interno di una certa sfera (non confondiamo sfera con curvatura dello spazio; la sfera indica solo il volume in cui deve essere contenuta la massa), come ricavato precedentemente.

(2) Il moto di un corpo è soggetto solo alla gravitazione, ossia alla curvatura imposta dalla massa.

Queste due leggi sono molto simili a quelle su cui si basa la meccanica classica. La prima è la legge di Newton sull’inverso della distanza; la seconda è la descrizione del moto conseguente. La relatività generale potrebbe essere scritta semplicemente come:

R = GE

Dove R è una costruzione matematica composta da 16 numeri in una matrice o tensore che descrive la distorsione dello spaziotempo. Essa sarebbe in pratica ciò che Newton indica con F. G è la costante di gravitazione (quella resiste sempre). E è un altro numero molto complicato, descritto anch’esso da un tensore, che rappresenta l’energia dell’oggetto. In parole molto semplici il prodotto delle masse di Newton, ma con qualcosa in più…

Potremmo scriverla in modo molto più esteso, ma possiamo limitarci a questo:

R_μυ - ½ Rg_μυ = 8 πG T_μυ/c⁴

Dove R_μυ è il tensore di Ricci, R la curvatura scalare, g_μυ il tensore metrico, T_μυ il tensore energia-impulso. Non illudiamoci, però, essa sembra una sola equazione, ma in realtà dà luogo a molte equazioni dipendenti dalle componenti dei tensori. 

Dopo aver introdotto, anche se in modo semplificato, il concetto di tensore, la formula di Einstein mette ancora meglio in luce il suo carattere fondamentale. Ogni componente dipende da operazioni svolte su componenti di altri tensori. Potete quindi immaginare a cosa si andrebbe incontro cercando di sviluppare nel modo più generale possibile quella "semplice" equazione. Resta l'invarianza rispetto al sistema, ma resta anche il bisogno di semplificare e ridurre il numero delle componenti dei vari tensori (imponendo il valore ZERO a qualcuna). Da qui nascono proprio le soluzioni particolari, sufficienti, comunque, a far prevedere buchi neri, l'effetto lente, le onde gravitazionali e molto altro ancora che un po' alla volta viene pienamente confermato dalle osservazioni.

Sperare in un miglioramento della teoria è sicuramente plausibile secondo almeno due fronti (almeno per me, ma non solo). Il primo è quello di capire come tutto ciò possa veramente estrapolarsi a grandi distanze dalla massa deformante (vedi velocità anomala delle stelle lontane dal centro della galassia) e come tutto ciò riesca a combinarsi perfettamente con la visione quantistica del microcosmo. Temo che bisognerà aspettare un altro Einstein...

"...Ma come ha fatto a pensarci?...", diceva Feynman. La risposta è forse molto semplice: "Lui è stato il primo a capire veramente il linguaggio con cui si parlavano tra loro gli attori dell'Infinito Teatro del Cosmo".