Questo articolo è inserito nella sezione d'archivio dedicata all'Elettromagnetismo

 

In questo articolo scriviamo le equazioni in versione differenziale, utilizzando i teoremi del rotore e della divergenza. Poi, tra un po', vedremo se risolvere le equazioni differenziali che portano alle onde elettromagnetiche...

Prima equazione

∫E x dA = Q/ε₀

Utilizziamo subito il teorema della divergenza che dice:

∫div(F) dV = ∫F x dA

Il  vettore F può diventare benissimo il nostro vettore E del campo elettrico, per cui abbiamo:

∫div(E) dV  =  Q/ε₀

A questo punto abbiamo un piccolo problema: da una parte vi è un integrale e dall'altra apparentemente no. Sembrerebbe di non aver fatto passi in avanti. Ma, attenzione, la carica Q può benissimo essere espressa in termini di densità di carica ρ = Q /V (è sempre una densità... ossia la carica divisa per il volume che la contiene), Ne segue:

Q = ρ V

Ma l'intero volume può essere tranquillamento espresso come la somma di tutti i volumetti, per cui:

∫div(E) dV = ρ V/ε₀ = ∫(ρ/ε₀) dV

A questo punto abbiamo due integrali entrambi estesi allo stesso volume e, qualsiasi esso sia, vale la regola che se i due integrali sono uguali lo sono anche le funzioni che vengono integrate, per cui:

div(E)  = ρ/ε₀

Per non farvi confondere quando andate a guardare in giro per la rete, questa espressione può essere sintetizzata con il simbolo usato oggi giorno per la divergenza, ossia ∇ x, o, ancora più utilizzato, ∇ •. Da cui, la prima equazione differenziale di Maxwell:

∇ • E = ρ/ε

Possiamo anche scrivere la divergenza come prodotto scalare tra un "vettore" derivata e un vettore di campo, ossia uno scalare che come componenti le tre derivate del campo rispetto ai tre assi cartesiani, ossia:

div(E) = ∇ • E = ∂Fx/∂x + ∂Fy/∂y + ∂Fz/∂z

Non arrabbiatevi, ma abbiamo ripetuto quanto già descritto nel primo articolo... La vera difficoltà delle equazioni di Maxwell sta proprio nel modo apparentemente diverso con cui si riescono a descrivere e che spesso crea confusione e/o dubbi...

Seconda equazione

Questa equazione è ovviamente la più semplice da trasformare...

∫B x dA  = 0

Basta scrivere nuovamente il teorema della divergenza...

∫div(F) dV = ∫F x dA

e sostituire F con B

Si ottiene:

∫div(B) dV = 0

Ma un integrale su un volume qualsiasi è uguale a zero se la funzione da integrare è uguale a zero, da cui:

div(B) = 0

o, se preferite:

∇ • B = 0

Notiamo ancora una volta la differenza sostanziale tra volume che contiene una carica elettrica e volume che contiene un dipolo magnetico. Nel primo caso o il flusso esce oppure entra. Nel secondo caso, tanto è il flusso che entra e tanto è quello che esce, dato che all'interno del volume vi è sia una carica positiva che negativa.

Terza equazione

∫E x dl = ∂(∫B x dA)/∂t

Andiamo a tirar fuori dal cappello il teorema del rotore, applicato al campo E ...

∫rot(E) x dA = ∫E x dl

Basta sostituire e otteniamo:

∫rot(E) x dA = ∂(∫B x dA)/∂t

Senza alcun problema possiamo inserire la derivata all'interno dell'integrale e otteniamo:

∫rot(E) x dA = ∫(∂B/∂t) x dA

I due integrali sono entrambi estesi alle aree e quindi, si possono eliminare:

rot(E) = ∂B/∂t

o, se consideriamo il moto degli elettroni:

rot(E) = - ∂B/∂t

Per completezza, scriviamola pure in termini "attuali":

∇ x E = - ∂B/∂t

Quarta equazione

∫B x dl = μ₀I + μ₀ε₀ ∂(∫E x dA)/∂t

riprendiamo il teorema del rotore, applicandolo al campo magnetico B...

∫rot(B) x dA = ∫B x dl

Non ci resta che sostituire nuovamente e ottenere:

∫rot(B) x dA = μ₀I + μ₀ε₀∂∫(E x dA)/∂t

Come abbiamo fatto per la densità di carica, così possiamo fare per la densità di corrente J, ossia:

I = ∫J x dA

da cui:

∫rot(B) x dA = μ₀∫J x dA +  μ₀ε₀∂∫(E x dA)/∂t

o, come fatto prima:

∫rot(B) x dA = ∫μ₀J x dA +  ∫μ₀ε₀ ∂E/∂t x dA

Per le proprietà degli integrali la loro somma è uguale all'integrale della somma (dato che si integra sullo stessa area), per cui:

∫rot(B) x dA =∫(μ₀J+ μ₀ε₀∂E/∂t) x dA

Eliminando gli integrali:

rot(B) = μ₀J+ μ₀ε₀∂E/∂t

o, cambiando notazione:

∇ x B = μ₀J+ μ₀ε₀∂E/∂t

Possiamo ora permetterci di riassumere  il significato delle quattro equazioni da un punto di vista differenziale:

1.  La prima equazione ci dice che la divergenza del campo elettrico è uguale alla densità di carica divisa per una costante, col segno più o meno a seconda del segno della carica. Il che vuol dire che ogni carica elettrica genera un campo elettrico.

2.  La seconda equazione ci dice che non esistono cariche magnetiche separate, ossia in ogni punto deve esistere sia una carica positiva che negativa.

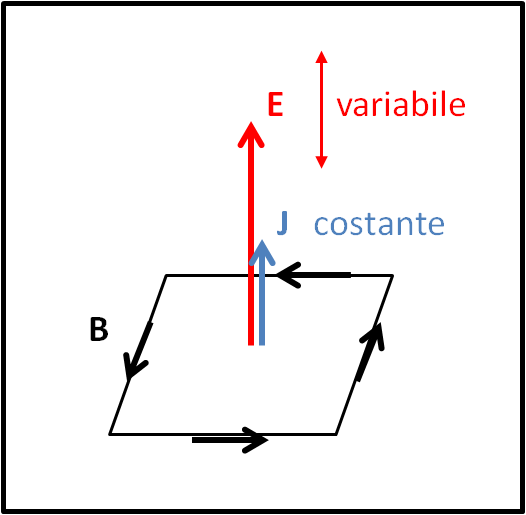
3.  La terza legge dice che un cambiamento del vettore campo magnetico crea una circolazione del campo elettrico . In altre parole una variazione del campo magnetico induce un campo elettrico (Fig. 24).

4. La quarta legge dice che una corrente elettrica e la variazione del campo elettrico generano un campo magnetico (Fig. 25).

Maxwell ha sintetizzato il tutto con una simmetria perfetta! Un attimo, un attimo... in realtà, la simmetria sarebbe perfetta solo se la seconda equazione fosse uguale alla prima, ossia se una carica magnetica fosse in grado di generare un campo magnetico. Accidenti! Si sta comunque cercando in tutti i modi di "scoprire" un monopolo magnetico. La rottura di simmetria sembra una cosa strana per l'Universo. Non dimentichiamo, infatti, quanto stia facendo  facendo impazzire i fisici l'abbondanza di materia rispetto all'antimateria. Qualcuno dice di avere prove sperimentali per l'esistenza dei monopoli magnetici, ma, per il momento, non vi è nessuna conferma decisiva.

Resta comunque il fatto (simmetria completa oppure no) che tutta la nostra vita è ormai legata all'applicazione delle quattro equazioni di Maxwell: basta accendere una luce, far partire un qualsiasi attrezzo elettrico, usare un computer e tutte le diavolerie moderne. Senza Maxwell saremmo forse veramente al BUIO completo e lo stesso Einstein non avrebbe pensato alla sua relatività. La faccenda, infatti, non è ancora finita. Le quattro leggi fanno intuire come campo elettrico e campo magnetico siano due facce della stessa medaglia e come le loro variazioni si svolgano su piani perpendicolari in perfetto accordo. Da qui alle onde elettromagnetiche il passo è (abbastanza) breve, così come lo è la costanza della velocità di propagazione di queste onde (la velocità della "luce").

Ci torneremo fra non molto...