Categorie: Matematica Riflessioni
Tags: Alice Lewis Carroll probabilità quiz tre sferette
Scritto da: Vincenzo Zappalà
Commenti:7
(QI) Le tre sferette di Alice ***
Chi non conosce Alice nel Paese delle Meraviglie? Sicuramente sia i bambini più ingenui sia i professori più esperti di meccanica quantistica. Il romanzo, infatti, anticipa la visione assurda dei fenomeni delle particelle quantistiche. Nel racconto si incontrano personaggi che rendono tangibili certi principi come l'effetto tunnel e, addirittura, la possibilità di universi paralleli. Non a caso oggi vengono chiamati con nomi legati alla strana favola esperimenti ai limiti delle conoscenza attuali, primo fra tutti lo Stregatto. Il fatto che compaia un gatto capace di sdoppiarsi sembra quasi richiamare l'altrettanto celebre gatto di Schroedinger. Un caso, ovviamente, ma è bello rileggere le avventure di Alice e scoprire analogie con una delle branche più complesse della fisica odierna.
Come dico spesso, sarebbe bello poter spiegare ai bambini, che ancora non hanno una visione deterministica della realtà legata alla fisica classica, gli accadimenti del meraviglioso Paese in cui tutto sembra andar contro la logica comune. Sono certo che proprio i bambini sarebbero in grado di accettare situazioni a dir poco assurde e potrebbero formarsi un visione alternativa della realtà del microcosmo, utilissima per la loro costruzione mentale verso un futuro sempre più ... quantistico.
Ma torniamo a Lewis Carroll, pseudonimo di Charles Lutwidge Dodgson (1832-1898). E' stato veramente un caso che la sua fantasia letteraria anticipasse in qualche modo la fisica non deterministica? I problemi legati al calcolo delle probabilità e alle operazioni di misura erano ben lontane dalle sue intenzioni? Mi sentirei di dire di NO. Lo scrittore, uomo molto poliedrico, si divertiva a costruire indovinelli e quiz dall'aspetto abbastanza semplice ma che, se letti attentamente, mostrano chiare analogie con le problematiche della MQ. Ne voglio riportare uno che, forse, ha dato proprio il via al più elaborato paradosso di Bertrand. Lo lascio come QUIZ, dato che logica e ragionamento possono portare alla soluzione anche chi è abbastanza digiuno di calcoli delle probabilità e statistica.
Abbiamo tre sferette: due gialle e una rossa. Mettiamone da parte una gialla. Quelle che rimangono sono sicuramente una gialla e una rossa. Senza guardare scegliamo una di queste due sferette e la mettiamo in un sacchetto di cui non possiamo vedere l'interno. Il colore della sferetta non scelta rimane del tutto sconosciuto.
PRIMO CASO
Davanti a noi vi è, dunque, un sacchetto, al cui interno vi è una sferetta che può essere sia gialla che rossa e che è stata scelta a caso tra una pallina rossa e una gialla. A fianco del sacchetto vi è la sferetta gialla accantonata fin dall'inizio.
La prima domanda è molto semplice: "Se estraiamo a caso una sferetta dal sacchetto, qual è la probabilità che essa sia gialla?".
SECONDO CASO
Andiamo avanti e inseriamo la sferetta gialla all'interno del sacchetto. Poi rimescoliamo ben bene ed estraiamo una sferetta. Guarda caso la sferetta estratta è gialla.
Ci troviamo esattamente nella situazione iniziale: abbiamo un sacchetto con al suo interno una sferetta che può essere sia gialla che rossa e accanto al sacchetto una sferetta sicuramente gialla. Non è cambiato assolutamente niente rispetto alla fase iniziale, per cui ci chiediamo: "Che probabilità abbiamo che la sferetta dentro al sacchetto sia gialla? "
TERZO CASO
Ricominciamo tutto da capo: inseriamo la solita sferetta che può essere sia rossa che gialla dentro al sacchetto. Poi inseriamo all'interno del sacchetto anche la sferetta gialla che avevamo accantonato.
Rimescoliamo ben bene ed estraiamo una sferetta SENZA, però, guardare il suo colore e la nascondiamo da qualche parte. Ci poniamo nuovamente la solita domanda: "Qual è la probabilità che la sferetta contenuta nel sacchetto sia gialla?"
Di seguito una figura che illustra schematicamente i tre casi:
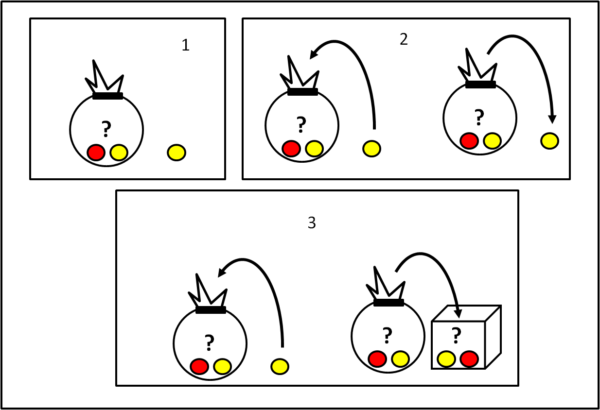
Forza e coraggio... non sono domande difficili, ma ci vuole una discreta dose di logica e di riflessione.
QUI la soluzione






7 commenti
Va bene, mi butto, anche se non so assolutamente gestire il calcolo delle probabilità. Lo insegnano ora nei licei?
1. Senza dubbio direi 50%
2. Non mi pare che si ricada nel caso precedente. Ora nel sacchetto c'è sicuramente una pallina gialla (quella aggiunta) è l'altra potrebbe essere G o R, per cui la probabilità di estrarne una gialla è maggiore, direi il 75%, quindi che nel sacchetto sia rimasta una gialla dovrei avere una probabilità minore, 25%?
3. Qui mi verrebbe da pensare a un terzo risultato intermedio, ma solo perché hai fatto riferimento al paradosso di Bertrand che dà tre risultati diversi.
Attendo la soluzione con ansia. È da un po' di giorni che ci penso
caro Albertone,
ovviamente la risposta alla (1) è giusta, ma poi...
non hai bisogno di saper gestire il calcolo delle probabilità, basta ragionare volta per volta su quanti casi si prospettino e su quanti di questi diano come risultato una sferetta gialla dentro al sacchetto.
Caro Enzo, probabilmente rischio di fare una brutta figura, ma d’altronde solo sbagliando e ragionando sugli errori s’impara.
Dunque, a mio avviso, ma non ne sono così sicuro:
Nel primo caso potendo scegliere solo su due palline di cui una rossa ed una gialla, c’è la medesima probabilità di pescare una pallina gialla o una rossa, ossia 1 pallina su 2:
CASO 1: Probabilità di pescare 1 pallina gialla = ½ (50%).
Anche se il secondo caso sembra simile al primo, in realtà si è già utilizzata (sprecata) 1 possibilità su 3 della pallina gialla di esser pescata, poiché è già stata estratta.
Pertanto considerato che la pallina gialla ha 2 probabilità su 3 di esser pescata e che ne ha sprecata 1:
CASO 2: Probabilità di pescare 1 pallina gialla = 2/3 -1/3 = 1/3 (33,3%).
Il terzo caso è ancora diverso, poiché non si il colore della pallina che è stata estratta e messa da parte.
Io lo considererei come se si dovesse estrarre una pallina su tre di cui due gialle ed una rossa, per cui:
CASO 2: Probabilità di pescare 1 pallina gialla = 2/3 (75%).
Che questa sia la situazione più favorevole per pescare una pallina gialla a me sembra ovvio (magari poi mi sbaglio), poiché già da subito potrei aver estratto una pallina rossa (anche se c’è 1 possibilità su 3), rimanendo con 2 palline gialle…
Non sono così sicuro di come ho calcolato l’ampiezza di probabilità, l’unica cosa di cui sono sicuro è che cambiando le condizioni iniziali, cambiano anche le probabilità di pescare una pallina gialla.
Paolo
Occhio che in (2) e (3) io sto chiedendo:
Che probabilità abbiamo che la sferetta dentro al sacchetto sia gialla?
Cioè intendi dire che nel caso 2 e 3 abbiamo il 100% di probabilità che nel sacchetto ci sia un sferetta gialla?
Ossia se nel secondo caso ho estratto una sfera gialla, nel sacchetto ne rimangono una rossa e una gialla, per cui sicuramente c'è una sfera gialla.
Nel terzo caso poco importa il colore della sfera che ho estratto, poiché nel sacchetto rimarranno una sfera gialla e una rossa oppure due sfere gialle, quindi sicuramente c'è una sfera gialla.
Oppure ho capito male?
Paolo
no, no... dentro al sacchetto rimane sempre e soltanto un sola sferetta: all'inizio può essere sia rossa che gialla. Poi ne inserisco un'altra che è sicuramente gialla, ma poi ne estraggo una che è sicuramente gialla e quindi all'interno ne rimane una soltanto che può essere nuovamente sia rossa che gialla. Qual è la probabilità che questa sia gialla?
Soluzione visiva (dove ogni colore indicato è un caso equiprobabile).
Caso 1)
G, R -> P(G) = 1/2
Caso 2)
Stato iniziale G, R, G,G stato finale G,R,G -> P(G) = 2/3
Caso 3)
Stato iniziale G, R, G,G = stato finale (perché l'estrazione non modifica lo spazio delle possibilità) -> P(G) = 3/4