Categorie: Meccanica quantistica
Tags: Born funzione d'onda onda probabilistica Schroedinger
Scritto da: Vincenzo Zappalà
Commenti:8
La funzione d'onda di Schroedinger. 1: il concetto **
Questo articolo è inserito in Meccanica Quantistica
Come spesso mi capita, a una richiesta precisa da parte di un amico-lettore ho subito risposto in modo drastico: "No, non è possibile.". Questa volta si tratta di Alberto e della sua richiesta di spiegare la funzione d'onda di S. In realtà, la trattazione matematica ha un aspetto non certo banale. Al momento spieghiamola solo concettualmente e poi ... si vedrà.
Partiamo da una premessa che in qualche modo abbiamo già compreso negli articoli sul principio di Heisenberg (PIH) e sulla lunghezza d'onda di De Broglie:
Non confondiamo il PIH con quello che viene chiamata "collasso" dei vari stati in cui si può trovare una particella quantistica. Il PIH è qualcosa di intrinseco della particella quantistica che avviene indipendentemente dalla operazione di misura. Il PIH descrive un comportamento tipico delle particelle duali, tale che in esse possano convivere contemporaneamente sia la natura ondulatoria (lunghezza d'onda, ossia quantità di moto) sia quella corpuscolare (posizione), restando nei limiti di una loro conoscenza approssimata. Ben diversa è, invece, la misurazione o, quantomeno, l'osservazione di una particella duale. Questa azione permette di perdere l'ambiguità, che è presente nella particella quantistica, ossia permette di localizzarla e di eliminare la sua natura duale. Quest'ultima operazione è quella che spesso viene chiamata "collasso" della funzione d'onda.
Ma cos'è la funzione d'onda?
Parliamone in modo puramente concettuale.
Cosa vuol dire avere a che fare con un comportamento ondulatorio? Beh... ormai lo sappiamo: non avere una posizione definita dell'entità che stiamo trattando. In altre parole, non sapere in che luogo di preciso stia la particella quantistica che sappiamo deve possedere entrambe le caratteristiche, istante per istante. Prima di effettuare qualsiasi osservazione di questa entità così ambigua, la particella deve vivere lo stato di onda e di corpuscolo. Tutto ciò che cosa vuol dire? Che la particella non si nasconde in un certo luogo all'interno dell'onda ma solo che non ha ancora nessuna posizione determinata. In realtà, è meglio dire che la particella esiste ovunque all'interno dell'onda, ma con diverse probabilità. Questo è l'unico modo possibile affinché possa realmente valere il concetto di dualità. La particella è sia onda che corpuscolo o, se preferite, essa non è mai o solo onda o solo corpuscolo.
Il fatto stesso che essa sia solo potenzialmente un corpuscolo fa sì che essa presenti anche la natura ondulatoria o viceversa. Tutto bello, ma come poter descrivere questa strana onda? E qui entra in ballo Schroedinger, il quale riesce a descrivere questa onda o meglio funzione d'onda. La particella può trovarsi ovunque all'interno dell'onda, ma la sua posizione è associata a una certa probabilità di esistere in un dato luogo in un certo istante. Attenzione, però... Questo non vuol dire che dobbiamo cercare di stanarla in qualche modo, ma che essa esiste realmente in ogni luogo (in modo da permettere la visione ondulatoria) con una certa probabilità.
Capiamo il concetto "assurdo" della MQ. La particella esiste come onda solo e soltanto perché essa non ha una posizione deterministica, ma solo probabilistica. L'essere ovunque ma con diverse probabilità dà luogo alla sua natura ondulatoria.
Finalmente entra in gioco l'osservazione. Se si osserva questa strana entità descritta dall'equazione di S. si riesce a far collassare la funzione che materializza la particella come corpuscolo. Collasso vuol dire passaggio da una posizione qualsiasi probabilistica a quella "reale". Ma se la particella diventa "reale" ossia esiste in un certo luogo in un certo tempo, è ovvio che perda del tutto la sua natura ondulatoria.
L'equazione di S. è perciò una descrizione matematica probabilistica del comportamento ondulatorio delle particelle, ossia ci dice come si distribuiscono le probabilità di avere la particella in un certo luogo in un certo istante (N.B. la natura probabilistica della funzione d'onda è stata introdotta da Born). Essa è la descrizione di un'onda dato che la particella può essere ovunque, ma perde questa caratteristica non appena la particella appare dal nulla. Ormai la probabilità che essa ha di essere in quel luogo è diventata il 100% e, di conseguenza, cade del tutto la sua natura ondulatoria. Si ha il cosiddetto "collasso" della funzione d'onda. Ciò è quello che capita guardando attentamente subito dopo le fenditure. Da quel momento in poi non abbiamo più onde ma solo corpuscoli. Non illudiamoci, però... possiamo tranquillamente descrivere e far collassare una funzione d'onda, ma il perché succeda tutto ciò è ancora inspiegato.
Possiamo fare un esempio tra la descrizione probabilistica del mondo normale e quella del mondo quantistico (da cui deriva anche il famoso gatto mezzo vivo e mezzo morto). Le figure che seguono sono tratte da "L'infinito dialogo tra Einstein e Bohr"):
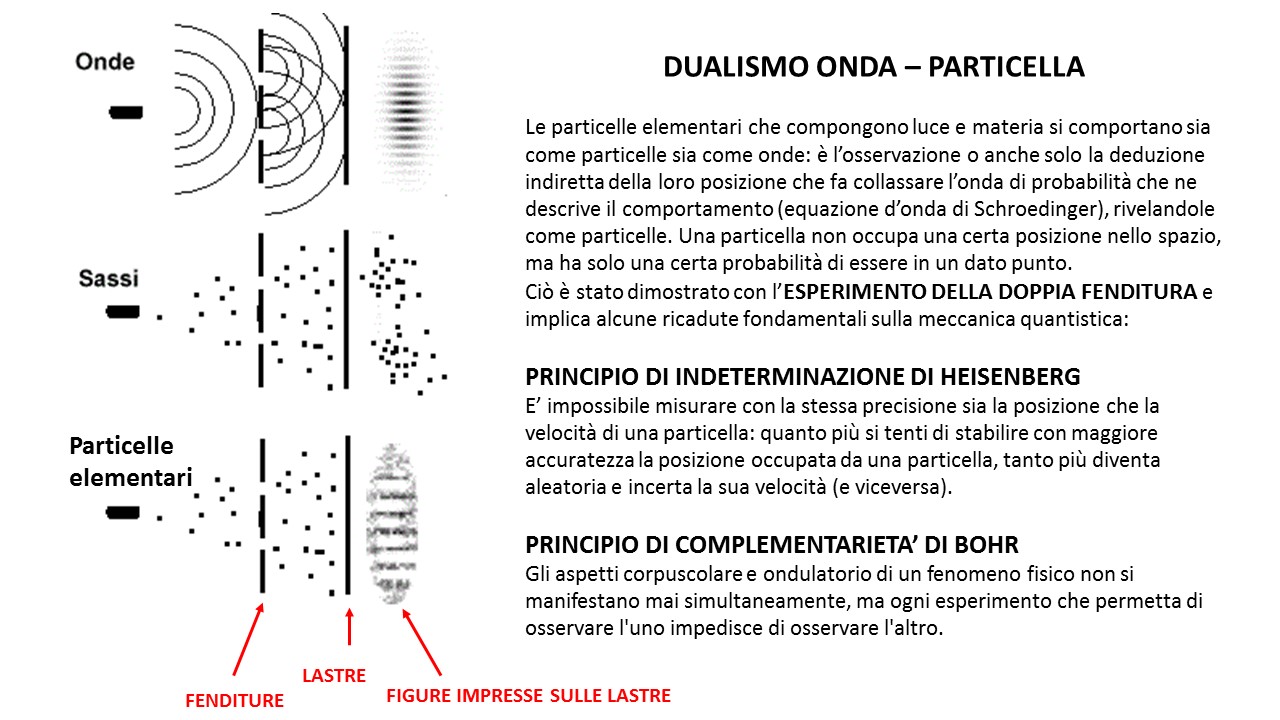

Alberto (ho scelto un nome a caso...) ha un carattere molto peculiare. Ogni mattina o si alza allegro e ottimista oppure triste e pessimista. Un amico comune mi chiede: "Di che umore è oggi Alberto?". Io non so cosa rispondergli se non dire che ha il 50% di probabilità di essere allegro e il 50% di essere triste. In qualche modo lo stato di Alberto viene descritto da una semplice legge probabilistica. Siamo quindi nelle condizioni della funzione d'onda di S. ? Assolutamente NO. Io non ho ancora osservato Alberto e quindi non so rispondere, tuttavia, lui sta già vivendo la giornata in modo ben definito. Il mio atto osservativo (l'incontro con lui) scopre la "realtà" dei fatti. Io posso descrivere il suo stato d'animo attraverso una funzione probabilistica, ma lui sta seguendo un comportamento deterministico: è quello che è! se Alberto fosse, invece, un elettrone, vivrebbe realmente in un regime probabilistico, ossia sarebbe proprio descritto come una funzione d'onda e solo l'osservazione deciderebbe il suo stato. La differenza è enorme: nel caso macroscopico il mio atto osservativo svela una realtà che già esiste, mentre nel caso microscopico decide proprio il suo modo di esistere.
Facciamo un altro esempio...
All'interno di una stanza c'è un ragazzino che ha a disposizione uno smartphone, un libro e un letto. A una certa ora mi accingo a entrare nella stanza. Prima, però, rifletto un attimo e dico tra me e me: "Quali sono le probabilità che stia usando lo smartphone, stia dormendo o stia studiando?". Guardando l'ora e conoscendolo bene posso creare una funzione d'onda probabilistica che mi descriva la situazione che troverò all'interno della stanza. Tuttavia, il ragazzino sta già facendo una delle tre azioni e io, entrando, posso solo scoprire qual è e valutare se la mia descrizione probabilistica era ben fatta. Se, invece, dentro la stanza ci fosse un elettrone, la sua posizione sarebbe veramente descritta da una legge probabilistica ed esso avrebbe tante probabilità di essere al centro e, magari meno di essere in qualche angolo. L'elettrone, però, si troverebbe in qualsiasi posizione con una certa probabilità, mentre il ragazzino si troverebbe in una e una sola posizione che ancora non conosco, ma posso immaginare. L'elettrone avrebbe, perciò, una vera natura duale. Il mio ingresso non scoprirebbe la verità ma indicherebbe in che posizione si viene a trovare in quel momento. Sono io che faccio collassare la funzione d'onda e distruggo la sua natura ondulatoria.
Nel mondo macroscopico il ragazzo prima del mio ingresso è davanti allo smartphone (con il 90% di probabilità) oppure sta dormendo (9 % di probabilità) oppure sta studiando (1% di probabilità). Nel mondo microscopico il ragazzo sarebbe sia davanti allo smartphone sia a letto sia davanti al libro con diverse probabilità. Notiamo bene la differenza: nel primo caso abbiamo una "o": o è qui o è li o è laggiù, nel secondo caso abbiamo una "e": il ragazzo è qui e là e laggiù, contemporaneamente.
E' esattamente ciò che capita al gatto di S. Essendo macroscopico non vive un'esistenza duale: o e vivo o è morto. Se, invece, fosse un elettrone sarebbe sia vivo che morto. Ribadisco, però: "Non chiedete il perché... questo lo sa forse solo Alice".
Possiamo anche tornare all'esperimento della doppia fenditura e rivederlo in modo più vicino al nostro scopo. L'elettrone passa SIA da una fenditura SIA dall'altra. Si comporta come un'onda. Io non lo osservo e aspetto che lo osservi (o lo MISURI) lo schermo finale, dove diventa particella è fa "bing". Il suo stato finale collassa, ma dopo che ha potuto viaggiare come onda e produrre interferenza. Se invece lo osservo prima, distruggo la sua natura ondulatoria e l'elettrone viaggia verso lo schermo già come particella. Farà nuovamente "bing", ma la sua natura duale è già sparita e non può più fare interferenza.
Potremmo anche dire che la seconda legge della dinamica Newtoniana del mondo macroscopico (F = ma) è equivalente all'equazione di S. nella meccanica quantistica. Entrambe descrivono matematicamente il comportamento delle entità che si stanno studiando. La prima descrive i moti del macrocosmo, la seconda descrive i comportamenti dei sistemi quantistici.
L'osservazione diventa perciò un'operazione di creazione o, se preferite, di collasso, ma chi può svolgere questa operazione rimane un mistero. Attenzione, quindi, al rischio di cadere nella psicofisica: deve essere cosciente oppure non importa assolutamente chi o cosa osservi la funzione d'onda? Agli elettroni & co. interessa veramente sapere chi o che cosa li osservi per prendere una certa posizione descritta dall'equazione di S. ? Questa parte fondamentale è ancora del tutto aperta e non descrivibile. Ribadisco: non abbiamo ancora capito niente della MQ. Stiamo entrando nel suo mondo in modo molto empirico, costruendo equazioni matematiche che possono anche essere corrette, ma cosa succeda realmente è ancora tutto da scoprire.
Beh... a questo punto, vi prometto che la prossima volta ricaveremo matematicamente (in modo semplificato) la funzione d'onda senza introdurre hamiltoniani o cose del genere.






8 commenti
Un grande regalo! Domani parto per lo Jutland e chissà che davanti all'isola di Helgoland non sia la volta buona che assimilo questa psi
Si, lo so che Helgoland è l'isola di Heisenberg, ho anche letto l'interessante libro di Rovelli, ma ad Arosa non sono mai stato, tanto meno con un'amante. Sono stato comunque all'istituto di fisica teorica di Copenaghen a cercare le orme di Bohr. E, giuro, mi sono un po' commosso
Buon viaggio e non dimenticarti di leggere la seconda parte...
Molto interessante, aspetto la seconda puntata
Salve, da quanto letto pare di conseguenza che non sia l'osservatore a determinare la posizione precisa che l'elettrone ha quando diventa particella. L'osservatore ne determina solo il momento, o sbaglio? In tal senso non sarebbe di conseguenza possibile che l'osservatore possa coscientemente influire sulla posizione dell'elettrone poiché non ne conosce la posizione (e non potrà mai farlo) al momento del colasso.
Articolo interessante, premetto che sono laureato in Ingegneria. Da un altro studioso avevo appreso anche che il collasso della funzione d'onda violerebbe i principi della relatività generale perchè avverrebbe in maniera istantanea; ma tutte queste trattazione che ho fatto anch'io a Ingegnerai riguardano la particella come singola entità mi piacerebbe capire come si comporta la particella all'interno dell'atomo cioè capire se è onda o particella o tutte e due come dice l'articolo.
Alcuni scienziati ritengono inoltre che l'osservato non abbia influenza sul posizionamento della particella una volta ottenuto il collasso in quanto comunque sia dovrebbe avvenire comunque anche per effetto delle irreversibilità dell'ambiente
caro Alex,
sull'argomento siamo tornati varie volte. In breve, posso dirti che l'elettrone all'interno dell'atomo si presenta come una nuvola di probabilità o , se preferisci, sotto stati diversi che collassano in uno solo quando viene rilevato da un'altra particella. L'osservatore può essere qualsiasi cosa e non un qualcuno cosciente. L'entanglement non viola assolutamente la RG in quanto non vi è scambio di informazione a distanza. Lo potrebbe fare solo se io riuscissi a manipolare una particella a piacere, ma questo non è possibile (ho scritto da poco un articolo a riguardo...).
Grazie professore, ieri al riguardo ho visto anche un video del prof Battiston che più o meno dice la stessa cosa sull'elettrone nell'atomo; complimenti per l'ottimo sito divulgazione che fortunamente ho trovato solo per caso