Categorie: Matematica
Tags: coseno equazione di Eulero identità di Eulero numeri complessi seno sviluppi in serie
Scritto da: Vincenzo Zappalà
Commenti:6
L'equazione e l'identità di Eulero **
Cari amici e, in particolare, caro Albertone, come promesso ecco due semplici metodi per ricavare la formula di Eulero e, conseguentemente l'identità di Eulero. Probabilmente, il nostro caro Umberto l'aveva già spiegata, ma vista la situazione attuale preferisco ricavarla di nuovo in modo veramente immediato (o quasi).
Primo metodo
Innanzitutto, andate a (ri)leggervi gli sviluppi in serie di ex, sin(x) e cos(x) (QUI e QUI). A questo punto scriviamoli qua sotto (anzi, per non perdere tempo e non rischiare di commettere qualche errore li ho recuperati in giro per la rete):
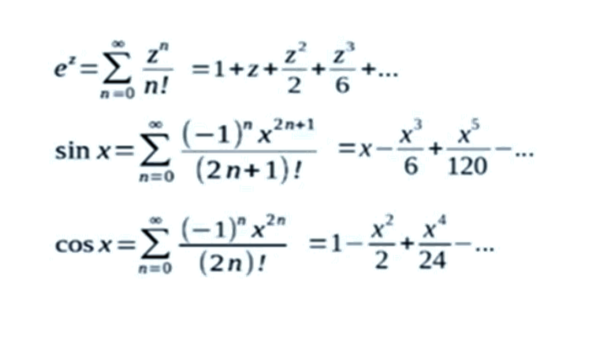
A questo punto, invece di scrivere ez, scriviamo eiy. Tuttavia, separiamo la sommatoria in due parti, la prima relativa ai valori pari di n e la seconda a quelli dispari. Otteniamo:
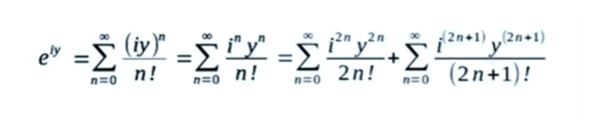
Sappiamo che:
i2n = (i2)n = (-1)n
e che:
i(2n + 1) = (i2)n i1 = (-1)n i
Sostituendo, abbiamo:
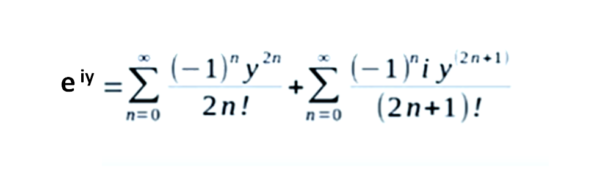
Ricordando gli sviluppi di seno e coseno, otteniamo proprio:
eiy = cos(y) + i sin(y)
Ossia l'equazione di Eulero.
Ponendo y = π si può scrivere la più bella formula del mondo (come diceva Feynman):
eiπ + 1= 0
Una semplice relazione che lega tra loro cinque costanti matematiche fondamentali: e, i, π, 1 e o.
Secondo metodo
Si può, però, ottenere anche in modo più semplice e senza scomodare gli sviluppi in serie.
Scriviamo la funzione g(x):
g(x) = eix/((cos(x) + i sin(x))
Facciamone la derivata rispetto a x:
g'(x) = ((eix i(cos(x) + i sin(x)) - eix(- sin(x) +i cos(x)))/(cos(x) + i sin(x))2
g'(x) = (eix i cos(x) + i2 eix sin(x) + eix sin(x) - eix i cos(x)))/(cos(x) + i sin(x))2
g'(x) = (eix i cos(x) - eix sin(x) + eix sin(x) - eix i cos(x)))/(cos(x) + i sin(x))2
g'(x) = 0
Ne segue che g(x) = costante
calcoliamola inserendo x = 0 nella funzione
g(0) = ei0/((cos (o) + i sin(o)) = ei0 = (ei)0/1 + 0 = 1/1 = 1
La costante vale quindi 1
Ne segue, infine, che:
g(x) = eix/(cos(x) + i sin(x)) = 1
eix = cos(x) + i sin(x)
e il gioco è fatto!
Va, comunque detta la verità... Il primo metodo ricava l'equazione finale lavorando sugli sviluppi in serie, il secondo, invece, parte da una funzione che già contiene l'equazione di Eulero e quindi presuppone già di conoscere l'equazione finale. Insomma, molto meglio il primo!
Contento Albertone?
6 commenti
...non è che si deve giustificare la validità degli sviluppi in serie citati quando dai numeri reali si passa ai complessi?
Cioè: chi mi garantisce che le serie convergano ancora nel campo complesso?
e perché non dovrebbero?
Mi pareva di ricordare che la convergenza delle serie in campo complesso non fosse una banalità. Mi ricordavo male, chiedo scusa...
Caro Enzo,
questo interessantissimo articolo sulla bellissima e geniale equazione di Eulero, mi fa pensare che è l'ennesima dimostrazione che la Matematica è un mare sterminato di logicità e ragionamento dove si immerge l'intelletto umano, e nel quale e dal quale sfociano e si dipartono ininterrottamente i fiumi di portata illimitata e perennemente in piena di arte, magia e fantasia...
Mi viene in mente qualche considerazione:
permettendomi di scrivere umilmente in maniera solo formalmente diversa l'equazione di Eulero, si può giungere alla identità (sempre nel campo dei numeri complessi):
che lega 3 operazioni algebriche fondamentali (elevamento a potenza, radice quadrata, logaritmo naturale) utilizzando un unico numero (negativo) per ottenere una costante fondamentale (oserei dire universale).
Così come negli sviluppi in serie che convergono alle funzioni trigonometriche seno e coseno, se si elimina il moltiplicatore^n)
(oppure si inserisce al suo posto )
), le serie convergono alle funzioni seno iperbolico e coseno iperbolico (che sono in effetti somme di funzioni esponenziali di base e), e anche qui la "magia" continua perché:
Chiedo venia per eventuali errori e/o inesattezze, ma la sostanza è che aveva proprio ragione il grandissimo Richard Feynman..
Parole d'oro caro Andy! Relativamente a Francesco, direi che , in fondo, i non è altro che una costante e come tale può essere maneggiata.
Iiiiih, troppa grazia, Vincenzo, sapevo di poter contare sulla tua somma disponibilità. Purtroppo non sono agile come voi; a una prima lettura mi sembra comunque tutto abbastanza alla mia portata. Ora dammi il tempo di rifletterci sopra e caso mai permettimi di venire ad elemosinare ulteriori ragguagli.
Grazie!