16/09/22

(Q) Rette parallele ***

Categorie: Matematica Tags: circonferenza geometria quiz rette parallele triangolo inscritto Scritto da: Vincenzo Zappalà Commenti:16

Un bel quiz puramente geometrico (senza trigonometria o coordinate cartesiane) presentato a un'olimpiade di matematica. Io ho seguito un certo procedimento, ma può darsi che ne esistano altri più rapidi ed eleganti. Sotto a chi tocca!

Il problema è il seguente:

Un triangolo acutangolo ABC è iscritto in una circonferenza. A partire da A stacchiamo su AB e AC due segmenti di lunghezza qualsiasi uguali tra loro (AD = AE). Tracciamo gli assi dei segmenti DB e CE che intersecano la circonferenza in F e G, rispettivamente. Dimostrare che le rette FG e DE sono parallele.

Vi aiuto, disegnando la figura...

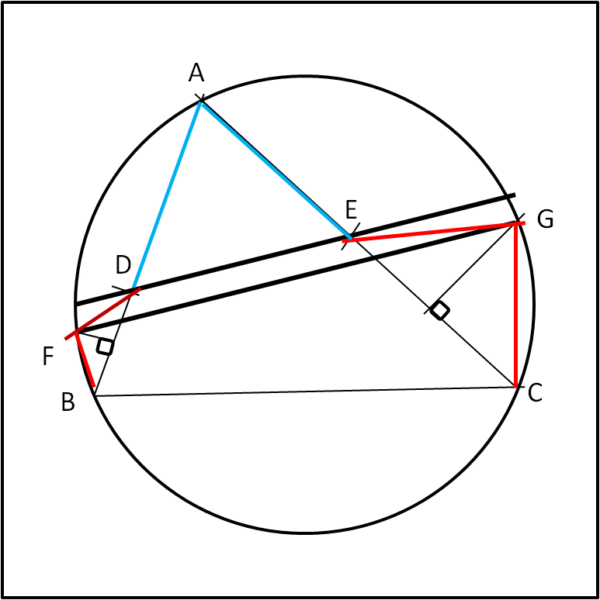
QUI la soluzione

16 commenti

Francesco

16/09/2022 at 22:01

Forse sbaglio (ricordare sempre: sono nella valle della disperazione di Dunning-Kruger) ma se prolungo il segmento HF a intercettare in K il prolungamento di DE e da K ne traccio la perpendicolare, considerato che l'angolo LFK è uguale a HFJ in quanto opposti al vertice, segue che l'angolo LKF è uguale a FJH in quanto complementari ad uno stesso angolo. Ma allora anche FKD (complementare di LKF) è uguale a LFK, alterni interni. Quindi le due rette sono parallele.

Attendo come al solito la smentita... :-(
Francesco

17/09/2022 at 06:59

Eccola qua, la smentita, me la faccio da solo: chi mi dice che l'angolo in L sia retto?

Ok, buttiamo via tutto...
Vincenzo Zappalà

17/09/2022 at 07:12

Più che altro direi che nessuno ti dice che sia retto l'angolo LKD. Quello in L lo puoi sempre costruire, ma poi...
Vincenzo Zappalà

17/09/2022 at 07:16

Vale anche il viceversa, come dici tu... resta il fatto che in entrambi i casi si considerano parallele le retta e poi si dimostra che lo sono... Direi che il problema è un po' più difficile.
Vincenzo Zappalà

20/09/2022 at 15:54

Vi vedo un po' in crisi... E' veramente così difficile? Aspetto ancora oggi e poi do la soluzione
leandro

20/09/2022 at 17:41

Io mi baserei sul circocentro ma non ho la soluzione
Vincenzo Zappalà

20/09/2022 at 17:58

Un piccolo aiuto... bisogna costruire una nuova circonferenza il cui raggio si ripete nella figura.
Vincenzo Zappalà

21/09/2022 at 15:44

Un ultimo aiuto...

per risolvere il quiz basta ricordare soltanto che gli angoli alla circonferenza di uno stesso arco sono uguali... L'importante è avere a disposizione DUE circonferenze.
Fabrizio

22/09/2022 at 02:46

Non ho trovato la soluzione geometrica richiesta.

Andando fuori tema, ho provato almeno a trovare una soluzione trigonometrica.

Riassumo il ragionamento che ho seguito.

Vogliamo dimostrare che se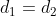 $d_1=d_2$ allora FG è parallelo a DE.

In queste figure ho ruotato la circoferenza in modo che DE sia orizzontale. E' solo una comodità grafica senza effetto sul ragionamento.

Concentro l'attenzione sulla costruzione attorno ad AB.

Poiché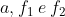 $a, f_1\: e\: f_2$ sono delle corde, le posso mettere in relazione con i rispettivi angoli.

$a=2 \sin{\left(\frac{\alpha}{2} \right)}$ $f_2=2 \sin{\left(\frac{\sigma}{2} \right)}$ $f_1=2 \sin{\left(\frac{\alpha-\sigma}{2} \right)}$

Per il teorema di Pitagora applicato ai triangoli che hanno in comune il cateto h:

$f_{1}^{2} - x^{2} = f_{2}^{2} - \left(a - x\right)^{2}$
da cui ricavo che: $x=\frac{a^{2} + f_{1}^{2} - f_{2}^{2}}{2 a}$

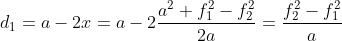
Quindi $d_1=a-2x=a-2 \frac{a^{2} + f_{1}^{2} - f_{2}^{2}}{2 a}=\frac{f_{2}^{2} - f_{1}^{2}}{a}$

Applicando le relazioni tra corda ed angolo che la sottende ottengo:
$d_1=\frac{4 \sin^{2}{\left(\frac{\sigma}{2} \right)} - 4 \sin^{2}{\left(\frac{\alpha}{2} - \frac{\sigma}{2} \right)}}{2 \sin{\left(\frac{\alpha}{2} \right)}}$

Applicando a questa espressione le identità trigonometriche di riduzione di potenza, duplicazione degli angoli e sottrazione, si ottiene questa semplice espressione:
$d_1=2 \sin{\left(\sigma - \frac{\alpha}{2} \right)}$

(ha la lunghezza di una corda di una circonferenza dello stesso raggio di quella in figura sotto un angolo di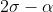 $2\sigma-\alpha$ , forse ha un significato geometrico che non ho trovato)

Analogamente per l'altro triangolo:
$d_2=2 \sin{\left(\rho - \frac{\beta}{2} \right)}$

Poichè abbiamo costruto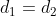 $d_1=d_2$ , segue che 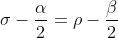$\sigma - \frac{\alpha}{2}=\rho - \frac{\beta}{2}$ vale a dire: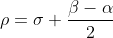 $\rho =\sigma+ \frac{\beta-\alpha}{2}$

Tracciamo il raggio perpendicolare ad DE. Chiamiamo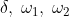 $\delta,\;\omega_1,\; \omega_2$ gli angoli tra questo raggio e quelli passanti rispettivamente per A, F, e G.

Affinché FG sia parallelo ad ED, deve essere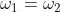 $\omega_1=\omega_2$ . Questa uguaglianza si può dimostrare considerando che

$\omega_1=\sigma+\delta$ e $\omega_2= \rho-\delta=\sigma+\frac{\beta-\alpha}{2}-\delta$

inoltre, considerando gli angoli che compongono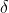 $\delta$ ,
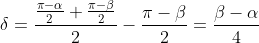
$\delta=\frac{\frac{\pi-\alpha}{2}+\frac{\pi-\beta}{2}}{2}-\frac{\pi-\beta}{2}=\frac{\beta-\alpha}{4}$

Allora $\omega_1=\sigma+\frac{\beta-\alpha}{4}$ e

$\omega_2=\sigma+\frac{\beta-\alpha}{2}-\frac{\beta-\alpha}{4}=\sigma+\frac{\beta-\alpha}{4}$

Quindi se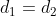 $d_1=d_2$ , allora 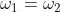$\omega_1=\omega_2$ ne segue che ED ed FG sono paralleli, quello che volevamo dimostrare.
leandro

22/09/2022 at 22:34

<a href="https://im.ge/i/1hnL26"><img src="https://i.im.ge/2022/09/23/1hnL26.IMG-20220922-222903.jpg" alt="IMG_20220922_222903" border="0"></a>

Soluzione senza trigonometria . Scusate l'immagine ma ho avuto problemi nel caricamento
leandro

22/09/2022 at 22:39

manca una spiegazione. HI è parallela alla retta tesa tra i due punti mediani perchè OH è parallelo al segmento da D alla circonferenza , idem per GI .
Vincenzo Zappalà

23/09/2022 at 07:43

Caro Leandro,

Dovresti chiarire meglio tutti i passaggi...
leandro

23/09/2022 at 13:00

Nella fretta avevo mescolato le lettere. Questa mi sembra migliore

L'angolo HOI è uguale a alfa + beta.
Ma OHI è triangolo isoscele, quindi OHI = pi/2 - ( alfa+beta)/2
HLN è per costruzione un triangolo rettangolo, quindi l'angolo HLN = pi/2 - OHI = pi/2 - pi/2 + (alfa+beta)/2 = (alfa+beta)/2
ovvero 2 HLN = alfa+beta
Osserviamo il triangolo ABC : l'angolo gamma = BAC = pi - (alfa +beta) , quindi

gamma = pi - 2 HLN

ADE è isoscele quindi l'angolo ADE = (pi -gamma)/2 = (pi - (pi-2 HLN))/2 = HLN
Poiché angolo ALI = HLN per opposizione, è alterno interno delle due rette DE e HI , esse sono parallele
Per costruzione i segmenti NQ = AD/2 = AE/2 = PR
NQ è ortogonale alle rette HO e FQ , quindi HO e FQ sono parallele
analogamnete lo sono le rette PI e RG . Esse sono inoltre equidistanti dello steso valore NQ =PR
Segue che l'angolo QFG è uguale all'angolo OHI , analogamente per RGF .
Da cui FG parallela a HI , parallela a DE .
cvd
<a href="https://im.ge/i/1i4DGa"><img src="https://i.im.ge/2022/09/23/1i4DGa.triangolo.jpg" alt="triangolo" border="0"></a>
Vincenzo Zappalà

24/09/2022 at 08:11

mi sembra tutto OK
Fabrizio

24/09/2022 at 11:23

Buona l'idea di Andy di dimostrare il parallelismo per un caso particolare per poi estenderlo agli altri casi, però mi sfugge qualcosa nella dimostrazione.

Non capisco l'ultima affermazione: '.... Segue che l'angolo QFG è uguale all'angolo OHI , analogamente per RGF . Da cui FG parallela a HI , parallela a DE ." . Detta così mi sembra che possa valere per tutti i punti sulle rette QF e RG. Non vedo dove entra in gioco il fatto che F e G devono essere sulla circonferenza.
Vincenzo Zappalà

24/09/2022 at 11:54

giusta affermazione, direi... il passaggio da HI a FG è un poco subdolo, E' un po' come se FG fosse costruita parallela a IH... Tutte le rette perpendicolari ad AB e ad AC portano allo stesso risultato se HN/FQ = Pi/RG

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.