Categorie: Matematica
Tags: angoli alla circonferenza geometria quiz rette parallele soluzione
Scritto da: Vincenzo Zappalà
Commenti:19
(Q) Soluzione del quiz su due rette parallele ***
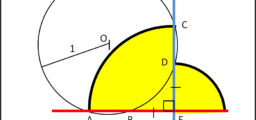
Consideriamo la figura inserita nel quiz e calcoliamo un po' di angoli e di lunghezze.
Prolunghiamo il segmento FD fino ad incontrare la circonferenza in X e il segmento EG fino ad incontrare la circonferenza in Z (Fig. 2).
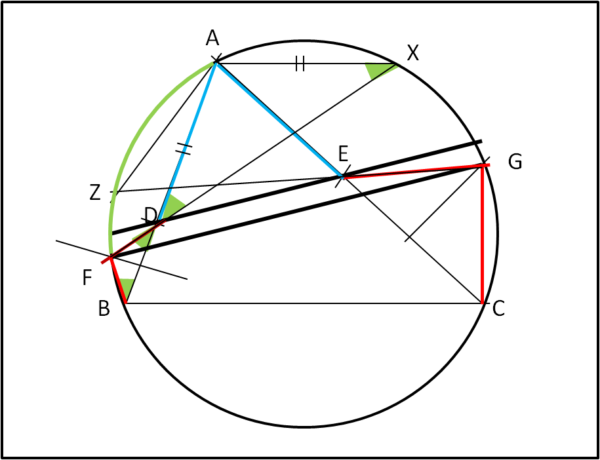
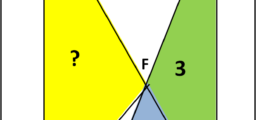
Consideriamo i due triangoli FDB ed ADX. Essi sono simili dato che hanno due angoli uguali: FDB e ADX perché opposti al vertice e FBA e FXA dato che sono angoli alla circonferenza di uno stesso arco AF.
Tuttavia, sappiamo che per costruzione FB = FD. Il che implica che, per la similitudine dei triangoli FDB e ADX, anche AX = AD. Ma AD è uguale ad AE per costruzione. Abbiamo quindi che
AD = AE = AX
Passiamo alla Fig. 3
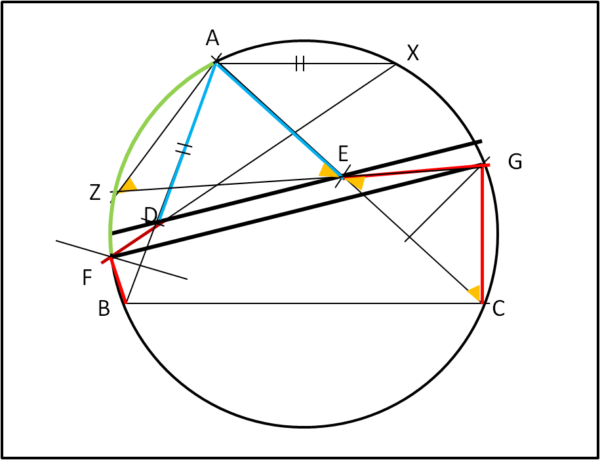
I due triangoli AZE e GCE sono anch'essi simili, per le stesse ragioni di quelli precedenti: AEZ = GEC perché opposti al vertice e AZG = ACG perché angoli alla circonferenza dell'arco AG.
Ma, dato che GC = EG anche AZ = AE.
In conclusione:
AD = AE = AX = AZ
Facciamo centro in A e tracciamo la circonferenza di raggio AD, come mostra la Fig. 4
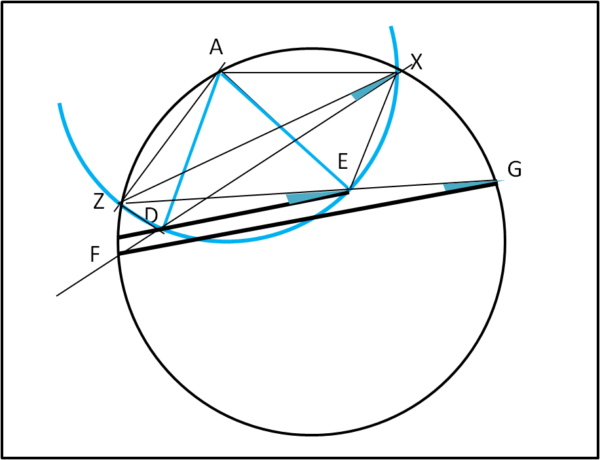
E poi tracciamo il segmento ZX. Dedichiamoci soltanto agli angoli...
ZGF deve essere uguale a ZXF dato che angoli alla circonferenza "nera" dell'arco "nero" FZ. Tuttavia sappiamo anche che ZXD = ZED perché angoli alla circonferenza "azzurra" dell'arco "azzurro" ZD. In definitiva, dato che ZXD = ZXF:
ZGF = ZXF = ZXD = ZED
ZGF = ZED
Il che implica che le due rette DE e FG devono essere parallele dato che formano uno stesso angolo con la retta ZG.
Niente male, vero?
QUI il quiz
N.B: Nei commenti trovate un metodo alternativo altrettanto valido ricavato dal nostro Fabrizio!



19 commenti
Niente male davvero!
Ma come arrivi a queste costruzioni che inizialmente sembrano divagare dal problema e poi piombano sulla soluzione?
Questo è un problema presentato alle olimpiadi di matematica e quindi si sa già che vi è sempre un qualche trucco che semplifica la soluzione.
Provo a dimostrarlo in un altro modo, prendendo a prestito l'immagine di Fabrizio (grazie).
Prolungo FN che incontri il prolungamento di DE in L e il prolungamento di PG in H. Prolungo PG che incontri il prolungamento di DE in M (più fatica a dirlo che a farlo...:-)
Chiamo 2a l'angolo in A.
Ora, l'angolo in N è retto per costruzione e LDN=ADE perché opposti al vertice. Quindi
NLD=a
Per la stessa ragione anche PME=a. Il triangolo LHM è quindi isoscele, con l'angolo LHM uguale al doppio di ADE.
Traccio da H la perpendicolare a FG. L'angolo FHK è la metà di LHM, quindi FHK=ADE e allora
HFK=a
Ma anche NLD (corrispondente a HFK) è uguale ad a, quindi FG è parallela a DE.
Stavolta spero di non aver fatto errori, anche se nella valle della disperazione di Dunning-Kruger è sempre pronto il mio posticino :-)
MA NO!!! Ancora sbagliato!
Chi mi dice che HK sia davvero la bisettrice di FHG? Uff!
Mi scuso se torno ancora su questo problema, ma lo consideravo una sfida: ero certo si potesse dimostrare in modo abbastanza semplice e ora credo di esserci riuscito.
Chiamo 2a l'angolo in A e d l'angolo in D.
Dal triangolo isoscele ADE si ha
pi = 2a + 2d .... (1)
Ora, l'angolo in N è retto per costruzione e LDN=ADE perché opposti al vertice. Quindi
NLD = a
Per la stessa ragione anche PME = a. Il triangolo LHM è quindi isoscele, e dalla (1) segue che
LHM = 2d.
Nel triangolo HFG pi = x + y + 2d, quindi sempre dalla (1) segue che
x + y = 2a .... (2)
Ora traccio il segmento NQ = NR e PT = PS, costruendo quindi i due triangoli isosceli QFR e TGS e considero i due quadrilateri CTGM e BQFL:
2pi = d + (pi/2 + y) + (pi - 2y) + a somma angoli interni di CTGM
2pi = d + (pi/2 + x) + (pi - 2x) + a idem per BQFL
sottraendo membro a membro arrivo finalmente a
0 = y - x -2y + 2x, cioè
x = y
Dalla (2) segue quindi x = y = a
e allora le rette DE e FG sono parallele, perchè x = a è corrispondente a FLD = a.
Giusto stavolta? :-)
Caro Francesco,
mi sembra che funzioni... bravo!
Scusate se faccio ancora l'avvocato del diavolo.
Credo ci sia una imprecisione nella valutazione dell'angolo TGM e dell'omologo QFL.
I loro valori dovrebbero essere rispettivamente pi-y e pi-x.
A prima vista mi sembrava che non inficiasse la dimostrazione cambiando nello stesso modo le due espressioni che vengono messe a confronto.
Purtroppo però, utilizzando i due nuovi valori nelle espressioni queste diventano:
2pi = d + (pi/2 + y) + (pi - y) + a=d+a+3 pi/2 somma angoli interni di CTGM
2pi = d + (pi/2 + x) + (pi - x) + a=d+a+3 pi/2 idem per BQFL
x ed y spariscono dalle espressioni e non credo si possa più dedurre da loro che x=y.
l'errore c'è e mi era scappato... Fabry, occhio di falco!!
Grazie Fabrizio, tutto vero... :-(
Francesco,
spero che tu abbia ancora voglia di cercare la soluzione più semplice. Faccio il tifo per il tuo tentativo. Mi piacerebbe poter capire il ruolo che ha la circonferenza che sembra quasi magico.
E' stato questo che mi ha fatto sospettare che nella tua ultima soluzione (ed in altre che ho commentato) ci fosse qualcosa che non andava.
In qualche modo nella soluzione dovrebbe avere un ruolo qualche proprietà della circonferenza o delle corde.
Se non ne facesse uso sarebbe valida anche per punti che non sono sulla circonferenza. Sarebbe un scoperta interessante, ma sembra che non sia così.
Spero che questo possa aiutare la tua ricerca che mi auguro riesca.
Grazie Fabrizio!
Sì continuerò a cercare fino alla fine :-)
Fine che, a dispetto delle incomprensibili attività di biden, putin e kim jong-un auguro a tutti non eccessivamente prossima...
Ciao
Forse ho trovato una dimostrazione alternativa. Enzo, la sottopongo alla tua verifica e degli altri frequentatori del circolo.
Premessa
La dimostrazione che ho trovato non mi sembra molto più semplice della dimostrazione dell'articolo di sopra, ma mette in luce il significato di "staccare dalle due corde segmenti di uguale lunghezza e di prendere gli assi dei segmenti restanti, DB e EC", che mi sembrava una formula magica.
Partirei proprio dalla proprietà che hanno gli “assi dei segmenti restanti”, proprietà che mi ha guidato nella dimostrazione.
La distanza dell’asse della corda AB dall’asse del segmento DB e uguale a quella dell’asse della corda AC dall’asse del segmento EC. Questa distanza è la metà di AD ( o AE, che è uguale) ed è indipendente dalla lunghezza delle due corde. La dimostrazione è nella figura sottostante.
Seguono due passi per arrivare all'obiettivo di dimostrare che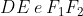 (vedi figura sotto) sono paralleli.
(vedi figura sotto) sono paralleli.
Nel primo passo utilizzo il risultato ottenuto sopra per dimostrare che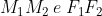 sono paralleli.
sono paralleli.
Nel secondo passo provo a dimostrare che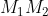 è anche parallelo a
è anche parallelo a 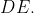 Seguirebbe (se tutto va bene) che
Seguirebbe (se tutto va bene) che 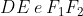 sono entrambi paralleli a
sono entrambi paralleli a 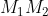 e, quindi, paralleli tra loro.
e, quindi, paralleli tra loro.
Nella figura sottostante ho tracciato le due corde (AB e AC), le intersezioni degli assi delle due corde con la circonferenza (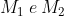 ) e le intersezioni degli assi dei segmenti DB e EC con la circonferenza (
) e le intersezioni degli assi dei segmenti DB e EC con la circonferenza (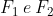 ).
).
Primo passo
La proprietà dimostrata nella premessa permette di affermare che gli angoli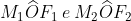 sono uguali poiché sottendono semicorde della stessa lunghezza (d/2). Chiamo
sono uguali poiché sottendono semicorde della stessa lunghezza (d/2). Chiamo 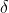 l’ampiezza di questi due angoli.
l’ampiezza di questi due angoli.
Derivo quindi che gli archi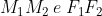 hanno la stessa bisettrice poiché l’arco
hanno la stessa bisettrice poiché l’arco 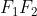 si ottiene aggiungendo all’arco
si ottiene aggiungendo all’arco 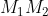 un arco di angolo al centro
un arco di angolo al centro 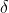 a entrambe gli estremi.
a entrambe gli estremi.
Di conseguenza, la corda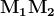 è parallela alla corda
è parallela alla corda 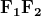 poiché gli archi che le sottendono hanno la stessa bisettrice, che è anche l’asse delle corde
poiché gli archi che le sottendono hanno la stessa bisettrice, che è anche l’asse delle corde 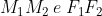 .
.
Secondo passo
Il prossimo obiettivo è dimostrare che la corda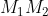 è parallela anche a
è parallela anche a 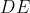 . Si avrebbe che
. Si avrebbe che 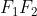 e
e 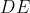 sono entrambi paralleli a
sono entrambi paralleli a 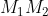 e quindi sarebbero paralleli tra loro, che è ciò che voglio dimostrare.
e quindi sarebbero paralleli tra loro, che è ciò che voglio dimostrare.
Traccio la retta tangente alla circonferenza in A. Chiamo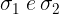 gli angoli tra la tangente e le due corde
gli angoli tra la tangente e le due corde  ed
ed  . Traccio anche la bisettrice dell’angolo
. Traccio anche la bisettrice dell’angolo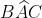 che interseca
che interseca 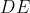 nel punto M.
nel punto M.
Noto che l’angolo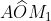 è uguale a
è uguale a 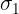 poiché la somma di ciascuno di loro con l’angolo
poiché la somma di ciascuno di loro con l’angolo 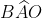 è 90°. Analogamente l’angolo
è 90°. Analogamente l’angolo 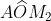 è uguale a
è uguale a 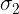 poiché la somma di ciascuno di loro con l’angolo
poiché la somma di ciascuno di loro con l’angolo 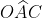 è 90°
è 90°
A questo punto è facile verificare che gli angoli e
e 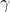 della figura sono uguali.
della figura sono uguali.
L’angolo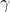 è un angolo alla base del triangolo isoscele
è un angolo alla base del triangolo isoscele 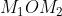 che ha l’angolo al vertice di ampiezza
che ha l’angolo al vertice di ampiezza 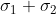 . Quindi
. Quindi }{2}) .
.
L’angolo è metà dell’angolo
è metà dell’angolo 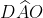 per costruzione. Vale a dire
per costruzione. Vale a dire }{2}) .
.
Quindi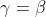 . La conseguenza logica di questa uguaglianza è che
. La conseguenza logica di questa uguaglianza è che 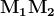 è parallelo a
è parallelo a 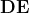 per la seguente catena di deduzioni. Poiché
per la seguente catena di deduzioni. Poiché 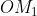 è perpendicolare a
è perpendicolare a 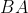 per costruzione e
per costruzione e 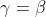 segue che
segue che 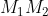 è perpendicolare a
è perpendicolare a 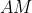 . A sua volta
. A sua volta 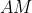 è perpendicolare a
è perpendicolare a 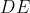 per costruzione. Quindi
per costruzione. Quindi 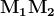 è parallelo a
è parallelo a 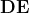 essendo entrambi perpendicolari allo stesso segmento
essendo entrambi perpendicolari allo stesso segmento 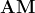 .
.
Poichè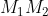 è parallelo sia a
è parallelo sia a 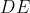 sia a
sia a 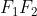 , come dimostrato sopra, consegue che
, come dimostrato sopra, consegue che
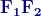 è parallelo a DE,
è parallelo a DE,
che è quello che volevo dimostrare.
caro Fabry,
oggi ho una giornata molto impegnativa... ma vediamo se qualche altro mate-moschettiere ha voglia di analizzare la tua soluzione!
Scusa Fabrizio,
ti chiederei di indicare nella prima figura gli estremi di s1, in modo che, indicandoli anche nella seconda figura, si veda bene la determinazione del valore di s1....
Enzo,
ho aggiornato le figure seguendo il tuo suggerimento. Ho anche corretto e aggiunto qualche informazione.
Se nel mio messaggio precedente si continuassero a vedere le vecchie figure, si può forzare il caricamento delle nuove figure con un click sul tasto refresh (normalmente è il circolino in alto a sinistra) tenedo premuto il tasto Ctrl della tastiera.
Per ogni evenienza le riporto anche qui sotto.
Ottimo direi!
Enzo, grazie per il tempo dedicato alla verifica della mia dimostrazione.
Soddisfatto per il risultato positivo, faccio una domanda alla quale non ho saputo rispondere.
La prima parte della mia dimostrazione è sostanzialmente algebrica. Ho provato a cercare un equivalente Euclideo senza successo. Si tratterebbe di dimostrare questa affermazione valida per due segmenti qualsiasi, non necessariamente corde:
"Dati due segmenti qualsiasi, AB e CD, scelgo un punto arbitratio su AB che chiamo E e un punto su CD, che chiamo F, tale che CF sia congruente con AE. Il segmento tra il punto medio di AB (M) ed il punto medio di EB (N) è congruente con il segmento tra il punto medio di CD (R) ed il punto medio di FD (S)."
Dimostrarlo algebricamente è quasi banale. Quale potrebbe essere una dimostrazione di tipo Euclideo?
P.S. Forse una potrebbe essere basata su quella nell'articolo sopra. Poi dai parallelismi arrivare alle congruenze, ma mi sembra troppo complessa per un problema apparentemente semplice. Inoltre non andrebbe bene per il mio caso poiché la uso proprio per dimostrare il parallelismo.
caro Fabry,
non so esattamente quando, ma vedrò di pensarci su ...
Non so se è euclideo, ma dovrebbe bastare... forse basta il primo passaggio.