Dietro alla domanda del titolo vi sta un concetto e una soluzione considerati ormai ovvi, ma che hanno avuto necessità di tutto il genio di Newton.

Il problema è: "Dato un corpo esteso a simmetria sferica di densità costante, la forza di gravità che esercita su un punto esterno è pari a quella esercitata dallo stesso corpo la cui massa sia concentrata nel suo baricentro". In altre parole, più sintetiche, un corpo sferico di una certa massa omogenea attira un punto esterno come se la sua massa fosse concentrata nel baricentro.

Beh... molti diranno: "Lo sappiamo bene, ce lo dice la legge di gravitazione Universale di Newton!". No, non è affatto vero, dato che la legge lavora su punti e non su corpi estesi.  Avevamo accennato a questo problema quando avevamo parlato del "buco attraverso la Terra", ma non lo avevamo affrontato, dandolo per scontato o quasi. E' giunta l'ora di farlo, ricordando che esso rappresenta il Primo Teorema del Guscio Sferico, mentre nell'articolo appena menzionato avevamo dimostrato il Secondo Teorema, quello relativo a un punto INTERNO al corpo sferico, decisamente più facile.

Ci sono vari modi per dimostrare il teorema, sia utilizzando la complicata trattazione dello stesso Newton, sia attraverso la trigonometria e l'integrazione, senza dimenticare quello che sfrutta il teorema di Gauss, relativo al campo elettrico, generalizzato per qualsiasi campo vettoriale.

Tutti questi metodi sono abbastanza complicati nei vari passaggi, ma, recentemente (2011), Christoph Schmid, dell'Univeristà di Zurigo ha presentato un lavoro in cui la soluzione è basata solo sulla particolare geometria e sul significato di valore medio. Potrebbe bastare la citazione, ma ritengo opportuno spiegare meglio i singoli passaggi che hanno portato alla dimostrazione finale. In qualche modo, questo metodo ribalta la situazione del punto P esterno alla sfera e lavora su un punto Q della sfera che si trova nella parte interna rispetto a una sfera immaginaria che passi per P.

La dimostrazione si separa in due parti, di cui la prima veramente ovvia.

(1) Direzione del vettore forza di gravità

Immaginiamo una sfera di massa M_T, di densità costante (ma la densità può anche variare, qualora tale variazione avvenga per pari distanza dal centro, cosa che si potrebbe applicare anche ai pianeti e alle stesse stelle) e un punto P esterno, di massa m, che è soggetto alla forza di gravità della sfera.

Dividiamo la sfera in tanti gusci sottilissimi e prendiamone uno a caso. Vogliamo dimostrare che la forza esercitata su P dal guscio sferico è diretta verso il centro del guscio. La dimostrazione è banale.

Consideriamo un elemento infinitesimo Q della sfera, di massa dM, tale da poterlo considerare puntiforme, posto a una distanza d da P. Tagliamo il guscio sferico con un piano che passi per Q, P e il centro del guscio (Fig. 1).

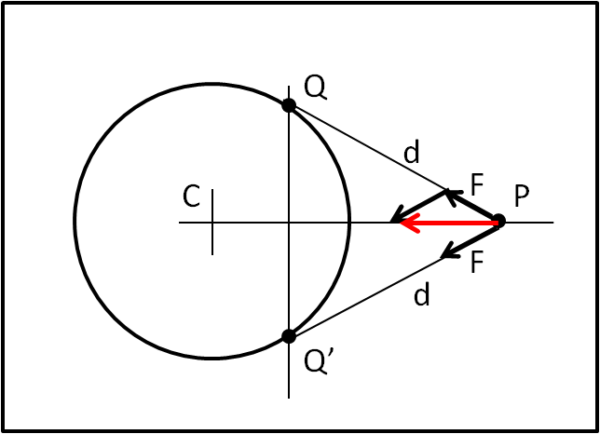
Il punto P è soggetto a una certa forza attrattiva che ha la direzione QP, ma, per la simmetria della circonferenza, esiste sempre un punto Q' tale da avere la stessa distanza d da P. Le due forze possono comporsi facilmente e la loro risultante è ovviamente diretta verso il centro C.

Cambiando piano di riferimento le cose non mutano, per cui tutti i punti di intersezione del cono, di vertice P ed asse PC, con il guscio sferico, danno luogo a una forza totale diretta verso il centro C. Ma il punto Q è stato scelto a caso e, quindi, può descrivere senza problemi un emisfero del guscio, mentre Q' descrive l'altro. Ne risulta che facendo la somma di tutte le forze che agiscono su P, la risultante continua a essere diretta verso il centro. In altre parole, il contributo di un guscio sferico è identico a quello di un unico punto, di massa pari alla somma di tutte le masse dM dei punti Q della guscio, posto nel centro C. Ma ciò capita per qualsiasi guscio sferico e ne segue che sommando tuti i contributi dei gusci sferici in cui può essere divisa la sfera iniziale, la forza F finale è sempre diretta verso il centro C.

Il problema, però, è ancora lontano dall'essere risolto... Abbiamo solo dimostrato che la forza di gravitazione è diretta verso il centro della sfera, ma non sappiamo ancora quale sia l'intensità della forza rispetto alla distanza r tra C e P. In altre parole, dobbiamo dimostrare che l'intensità di tale forza è pari a quella che si otterrebbe ponendo l'intera massa della sfera nel suo centro, ossia a una distanza r da P. Attenzione, quindi... una cosa è dire che la forza finale è diretta verso il centro C e un'altra cosa è dire che l'intensità di tale forza è legata solo alla distanza PC = r.

Quello che possiamo sicuramente dire è che se il punto P descrivesse una sfera attorno alla sfera iniziale, esso sarebbe sempre soggetto a una forza di pari intensità, ma nulla possiamo dire sulla intensità di tale forza.

(2) Intensità della forza

Quest'ultima sicurezza ci regala, però, un approccio geometrico per risolvere la questione. Consideriamo, perciò, nuovamente la nostra sfera iniziale (SI), ma questa volta introduciamo una sfera di raggio r (maggiore del raggio della sfera iniziale, ovviamente) in cui possa muoversi P, sapendo che in qualsiasi posizione esso sia, subirebbe una forza sempre costante da parte della sfera iniziale di massa M_T. Chiamiamo il luogo descritto da P come superficie dell'osservatore (SO). In poche parole, invertiamo i ruoli tra i punti della sfera e quelli, P, che subiscono la forza gravitazionale. Ossia, invece di far variare Q sul guscio, facciamo variare P e manteniamo fisso il punto Q.

Per ogni posizione di P, quest'ultimo avrà un'accelerazione g che lo porta verso Q (inteso come elemento infinitesimo, di massa mQ, del guscio) ed essa è data dalla legge di Newton:

g = Gm_Q/d²                   .... (1)

Ricordiamoci ancora, per non fare confusione, che la legge di gravitazione è conosciuta per corpi puntiformi, ma noi vogliamo vedere cosa succede per un corpo esteso a simmetria sferica.

La formula dell'accelerazione della (1) si applica la legge di Newton tra due punti. Tuttavia, sapendo che il contributo di tutta la Sfera Iniziale causa un' accelerazione sul punto P diretta verso il centro C, occupiamoci proprio di questa componente dell'accelerazione (Figura 2).

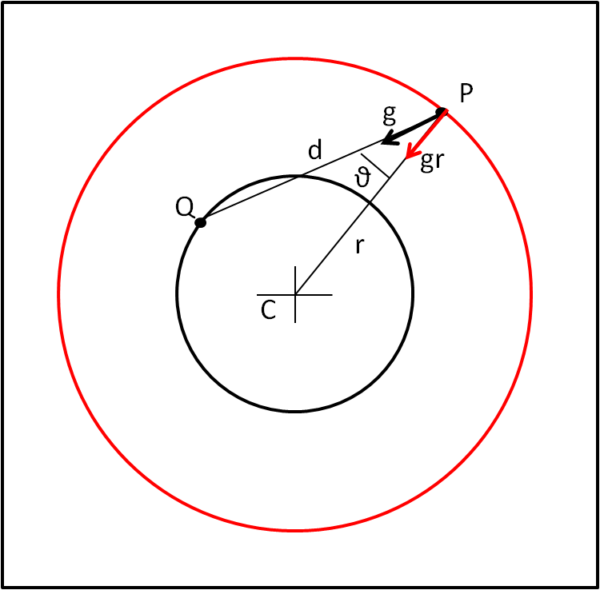
Per ogni punto P possiamo scrivere:

g_r = g cos θ = Gm_Q cos θ/d²         .... (2)

Facciamo ruotare, adesso, il punto P lungo la circonferenza di centro C e raggio r. Facendo questa operazione varia la distanza d tra Q e P, così come l'angolo θ, ma si può facilmente calcolare il valore medio dell'accelerazione <gr> (Fig. 3).

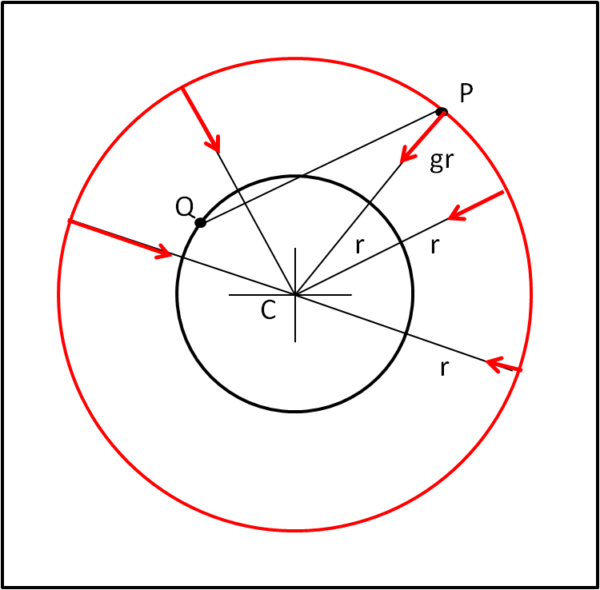
Il valore medio, però, non cambia al variare di Q, dato che non cambia la configurazione, ma viene solo ruotata. Ossia, <gr> è una costante per ogni punto Q della SI (Fig. 4).

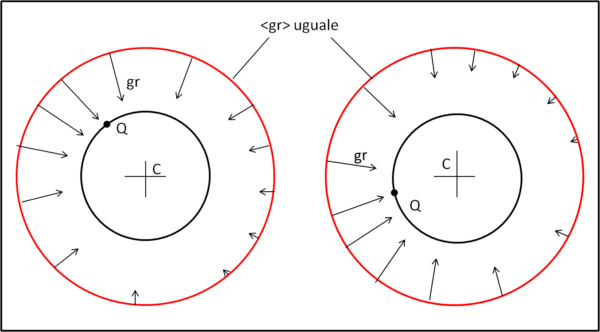
Torniamo al nostro punto P e stabiliamo per bene che cosa rappresenta. Esso non è altro che una piccolissima area A_P attorno al punto P.

Scriviamo la relazione gr · A_P (in pratica è la gr "pesata" in base alla superficie a cui è applicata... qualcosa come il flusso vettoriale). Tuttavia, Q non vede A_P, ma la sua proiezione A_P' = A cos θ.

Questa proiezione viene vista da Q attraverso un piccolo angolo solido Ω^(*). Sappiamo però che in una circonferenza si può scrivere una parte di essa come il prodotto tra l'angolo α e il raggio (Fig. 5).

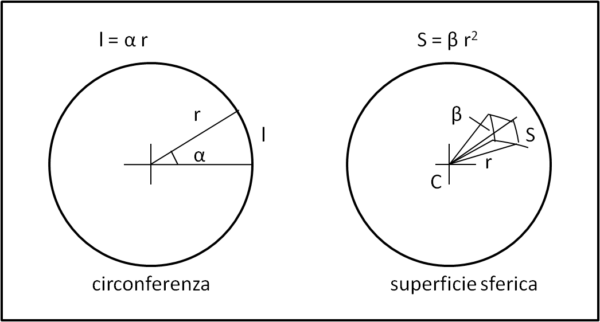
Ossia:

l = R α

Per una sfera, vale la relazione:

S = R² β

Come detto precedentemente, nel nostro caso dobbiamo moltiplicare A_P per il coseno di θ per ottenere la superficie vista da Q. Abbiamo perciò:

A_P cos θ =  d² Ω

A_P = d² Ω/ cos θ

Moltiplichiamo ambo i membri della (2) per A_P:

g_r A_P = (Gm_Q cos θ/d²)(d² Ω/cos θ) = Gm_Q Ω

Come per miracolo sono spariti sia d che il cos θ...

Non ci resta che fare la somma di tutti contributi al variare di P (e quindi A_P) sulla sfera di osservazione. Al posto del valore variabile g_r possiamo inserire il valor medio <g_r> che è una costante. Il valore medio esce dalla sommatoria. La somma degli angoli solidi Ω diventa l'angolo solido di una superficie sferica, ossia vale 4π. Otteniamo perciò:

∑g_r A_P = ∑Ω Gm_Q = 4π Gm_Q

<g_r>∑A_P  = 4π Gm_Q

<g_r> 4πr² = 4π Gm_Q

<gr> = 4π Gm_Q/(4 πr²)= Gm_Q/r²

<gr> = Gm_Q/r²                  .... (3)

Notiamo bene che questo risultato non dipende dalla posizione di Q. Per ogni punto Q avremmo lo stesso risultato, per cui ogni punto, con la sua massa m_Q, può essere portato al centro della sfera aumentando la massa ivi concentrata  fino ad ottenere M_G, dove M_G è la massa del guscio:

<g_r> = ∑Gm_Q/r² =  GM_G/r²

Ricordiamo che il valore medio <g_r> è sempre lo stesso per ogni punto Q e quindi sommando una serie di valori che hanno tutti la stessa media, la media finale resta la stessa. (Fig. 6)

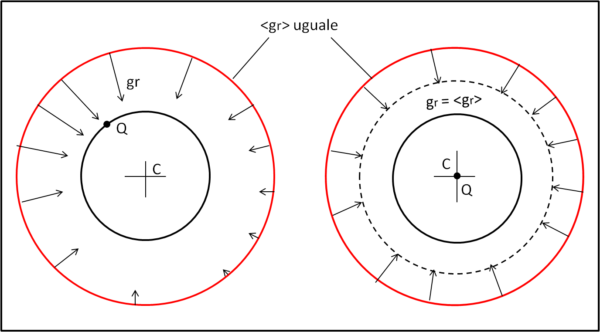
Tuttavia, non basta ancora... la media così ottenuta vale per un guscio, ma sappiamo bene che non dipende dalla posizione del punto Q, ossia esso si può trovare anche su un altro guscio e il valor medio di g_r resta invariato. Per cui al posto di M_G possiamo inserire la massa di tutta la sfera iniziale.

<g_r> = GM_T/r²

In poche parole, ogni punto P è soggetto a un'accelerazione che è proprio quella di un punto di massa M_T posto al centro della sfera. Possiamo tranquillamente dire che il valor medio perde di significato, dato che la relazione precedente vale per ogni punto P della SO.

g_r = GM_T/r²

La forza F che agisce su P vale, infine:

F = GM_Tm/r²

c.v.d.

 

(*) Cos'è l'angolo solido?

Data una certa superficie di area A e un punto V  a distanza r, si traccino le semirette passanti per V e per il contorno della superficie di area A.  si definisce angolo solido Ω la parte di spazio compresa tra queste semirette.

La definizione si comprende rapidamente attraverso la Fig. 7.

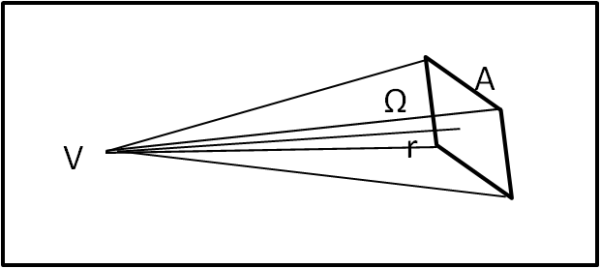
L'angolo solido, in analogia con l'angolo piano, si misura in steradianti, ossia facendo il rapporto tra area della superficie A e la distanza r al quadrato, ossia:

Ω = A/r²

Nel caso che A appartenga a una superficie sferica di raggio r, si calcola facilmente l'angolo solido dell'intera superficie sferica:

Ω = 4πr²/r² = 4π

Il risultato è analogo al caso di un angolo piano di una circonferenza di raggio r:

θ = l/r = 2πr/r = 2π