Dal teorema di Pitagora alla spirale di Teodoro (di Andy)
Questo articolo nasce come una serie di considerazioni e prove numeriche “sul campo” relative al teorema di Pitagora e all’ipotesi di Enzo su di una sua estensione a qualsiasi poligono, che ha ottenuto un primo riscontro particolare grazie alla “riscoperta” della spirale di Teodoro di Cirene. L’ipotesi di Enzo era quella di vedere, se possibile, l’applicabilità del teorema di Pitagora anche a poligoni con più di tre lati. Così ho deciso di tentare algebricamente se fosse stato possibile trovare una identità di tipo pitagorico (inizialmente limitata solo per valori interi) per poligoni generici con più di tre lati.
In poche parole, volevo vedere se esistessero quadruple, quintuple, sestuple, n-uple, di tipo pitagorico.
La spirale, oltre che a regalare graficamente tutte le radici quadrate dei numeri interi, riesce anche a costruire poligoni di n- 1 lati interi, tutti uguali fra loro tranne l’ultimo, per cui vale l'ipotesi di partenza. Ovviamente, partendo da un triangolo rettangolo, la costruzione di Teodoro può anche estendersi a poligoni con n lati tutti diversi tra loro e non interi. Resta, però, il vincolo dell’angolo retto di partenza.
Io ho invece affrontato il problema per via algebrica, nel modo più generale possibile, senza nessun vincolo sull’esistenza di un angolo retto.
Andy
E noi salutiamo il primo articolo di Andy, attento lettore da molto tempo che ha spesso elaborato procedimenti matematici del tutto personali e di grande interesse. Ci auguriamo che sia il primo di una lunga serie. Benvenuto Andy!
Consideriamo un poligono generico di n lati, e poniamo che un lato sia di misura dispari, n – 3 lati di misura pari, indicandoli con:
d = intero dispari qualsiasi, e p1 , p2 , p3 , …., pn-3 = interi pari qualsiasi;
il penultimo lato sia m, e l’ultimo lato sia m + 1.
Se si pone la condizione d2 + p12 + p22 + …. + p2n-3 + m2 = (m + 1)2 (1)
noti d, p1 , p2 , …. , pn-3 si può ricavare il valore di m e di conseguenza di m + 1, affinché sia soddisfatto il requisito che l’area costruita sul lato maggiore sia pari alla somma delle aree costruite sui restanti lati.
Sviluppando la (1) : d2 + p12 + p22 + …. + p2n-3 + m2 = m2 + 2m + 1
ed eliminando i due m2 presenti al primo e secondo membro → d2 + p12 + p22 + …. + p2n-3 = 2m + 1
da cui m = (d2+ p1 2 +p2 2 +....+ pn−32 −1)/2 ↔ m = [(d2−1)+ p1 2 +p2 2 +....+ pn−32]/2
Il numeratore della frazione è sicuramente pari, perché vi è il quadrato di un dispari d2 che è sempre dispari ma meno l’unità diventa pari; tutto il resto è somma di quadrati pari e quindi quantità pari; dividendo per 2 sicuramente si otterrà un intero pari.
Proviamo a fare qualche verifica numerica partendo proprio da un triangolo di lati rispettivamente d, m, m + 1:
3 lati: m = (d2−1)/2
se d = 3 → m = 4 m + 1 = 5
se d = 5 → m = 12 m + 1 = 13
se d = 7 → m = 24 m + 1 = 25
se d = 13 → m = 84 m + 1 = 85
e così via.
Come si può notare, vengono prodotte determinate terne pitagoriche, per cui il triangolo sarà di tipo rettangolo.
Passando ad un poligono a 4 lati:
m = (d2+ p1 2 −1)/2
se d = 3 p1 = 2 → m = 6 m + 1 = 7 → 32 + 22 + 62 = 72
Osservando solo 3 delle innumerevoli configurazioni geometriche che possono dar luogo i 4 lati con queste misure:
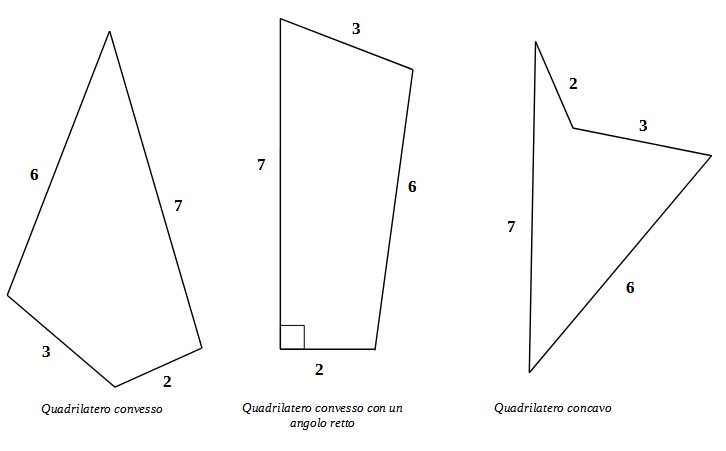
si può notare che il quadrilatero può essere indifferentemente convesso, concavo, può contenere un angolo retto oppure
no, ma rispetta lo stesso il requisito di “pitagoricità”.
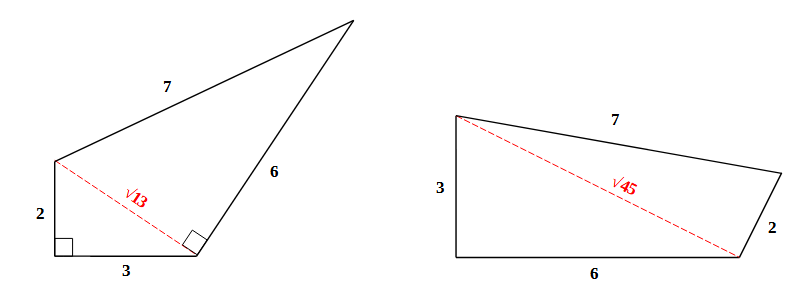
Ma se si costruisce un’altra coppia di configurazioni, partendo da un triangolo rettangolo, si rientra nella costruzione
già proposta da Enzo, e che richiama il triangolo generatore della spirale di Teodoro di Cirene, trattata come sempre
dettagliatamente dal nostro Enzo, con la differenza che qui il triangolo rettangolo di partenza non è isoscele ma la
sostanza del ragionamento non cambia.
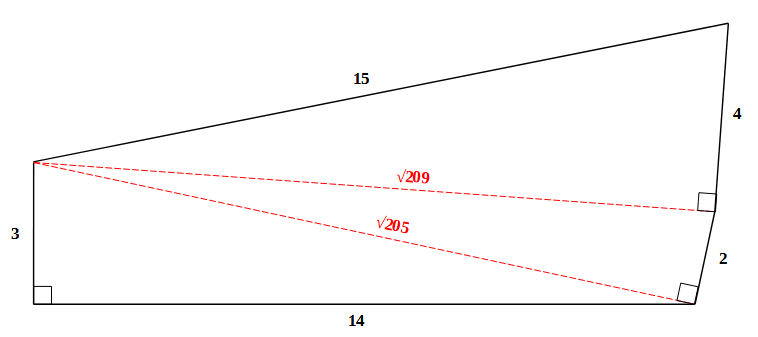
Passiamo adesso ad un poligono a 5 lati:
m = (d2+ p1 2 +p2 2 −1)/2
e inserendo sempre dei valori interi casuali dispari per d e pari per p1 e p2 :
d = 3 p1 = 2 p2 = 4 → m = 14 m + 1 = 15 → 32 + 22 + 42 + 142 = 152
Per un poligono a 6 lati:
m = (d2+ p1 2 +p2 2 + p32−1)/2
d = 11 p1 = 4 p2 = 14 p3 = 10 → m = 216 m +1 = 217 → 112 + 42 + 142 + 102 + 2162 = 2172
e così via per qualsiasi poligono generico di n lati.
Un caso particolare della regola generale è quello per il quale, dato un lato dispari d, gli n – 3 mediani sono tutti uguali tra loro.
Per un quadrilatero la (1) si riduce a: d2 + p12 + m2 = (m + 1)2 (2)
ma dato che i lati mediani sono uguali sarà:
p1 = m → d2 + m2 + m2 = (m + 1)2 → d2 + 2m2 = m2 + 2m + 1
che diventa m2 – 2m + d2 – 1 = 0 equazione di 2o grado con incognita m
la cui soluzione positiva è m = √(2−d2)+1 con 2 – d2 ≥ 0 (3)
ma siccome il più piccolo d intero dispari è 1, sostituendolo nella (3) si avrà che m = √(2−12)+1 = 2
e il quadrilatero avrà lati di misura 1, 2, 2, 3 → 12 + 22 + 22 = 32
Ovviamente la relazione rimane valida inserendo un moltiplicatore k, con k numero reale positivo:
(k×1)2 + (k×2)2 + (k×2)2 = (k×3)2
Ma tornando al quadrilatero 1, 2, 2, 3 se si disegna una specifica configurazione
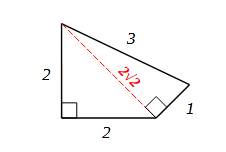
anche questa si riconduce al triangolo generatore della spirale di Teodoro di Cirene, con la differenza che qui il triangolo rettangolo isoscele di partenza è di lato 2, ma il risultato geometrico è sempre lo stesso.
Passiamo al caso particolare applicato ad un poligono di 5 lati considerando il dispari minore di lunghezza unitaria e gli n – 3 mediani di lunghezza 2:
m = (12+22+22−1)/2 = 4 , quindi avremo un 5-poligono di lati 1, 2, 2, 4, 5 → 12 + 22 + 22 + 42 = 52
e la costruzione geometrica è analoga alla precedente:
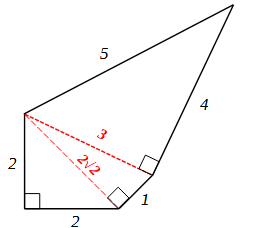
Per un 6-poligono, m = (12+22+22+22−1)/2 = 6 → 12 + 22 + 22 + 22 + 62 = 72
Anche in quest’ultimo caso si può costruire una figura geometrica per triangoli rettangoli successivi come fatto in precedenza.
E ovviamente la relazione rimane valida inserendo un moltiplicatore k, con k numero reale positivo:
(k×1)2 + (k×2)2 + (k×2)2 + (k×2)2 + (k×6)2 = (k×7)2
Estensivamente si può applicare la regola a qualsiasi poligono generico di n lati, come ad esempio al miriagono, poligono dotato di 10000 lati, per il quale occorre un microscopio per distinguerlo da una circonferenza. Praticamente, applicando il metodo dell’esaustione di Archimede, circonferenza circoscritta al poligono, circonferenza inscritta nel poligono e poligono stesso, apparirebbero tutti sovrapposti su di un’unica circonferenza.

Un dettaglio ingrandito del miriagono rende l’idea:

dove la distanza tra i singoli puntini rappresenta un micro-lato del poligono.
Quindi nel caso di un miriagono non regolare, considerando sempre d = 1, gli n – 3 lati mediani p uguali a 2, il lato “vice maggiore” m e il lato maggiore m + 1:
m= (12 + 9997×22−1)/2 = 9997×2 = 19994 → 12 + 9997×22 + 199942 = 199952
Per concludere, qualunque sia il numero (maggiore di 3) di lati del poligono, il metodo della costruzione geometrica a spirale partendo da un triangolo rettangolo generatore, segue la legge:
d2 + p12 + p22 + …. + p2n-3 + m2 = (m + 1)2
Qualcuno potrà chiedersi: e se invece di partire da un quadrato dispari e una somma di quadrati pari si partisse da un quadrato pari ed una somma di quadrati dispari?
Bene, ci viene in aiuto la formula principale, permutando d con p
p2 + d12 + d22 + …. + d2n-3 + m2 = (m + 1)2 da cui m = (p2 + d12 + d22 + …. + d2n-3 – 1) /2
Ora, se i d2 sono di numero dispari, la loro somma è dispari ma meno l’unità diventa pari, p2 è pari quindi il numeratore della frazione è senz’altro pari:
poligono a quattro lati: p = 4 d = 7 → m = (42 + 72 – 1)/2 = 32 m + 1 = 33
poligono a 6 lati: p = 2 d1 = 9 d2 = 13 d3 = 5 → m = (22 + 92 + 132 + 52 – 1)/2 = 139 m + 1 = 140
ma per un poligono a 5 lati: p = 8 d1 = 3 d2 = 15 → m = (82 + 32 + 152 – 1) /2 = 297/2 m + 1 = 299/2
la regola verrebbe rispettata ma non la condizione dei lati tutti di misura intera.
Sarebbe valida con tutti numeri interi solo per poligoni che presentano un numero di lati pari.






2 commenti
Devo un grandissimo grazie ad Enzo e Daniela per il loro supporto profuso durante la redazione dell'articolo e per la loro magna pazienza...
Una piccola precisazione;
ancora più in generale, l'identità pitagorica estesa può essere scritta come:
cioè i quadrati dei numeri pari possono ripetersi indifferentemente per un numero pari o dispari di volte.
mentre i quadrati dei numeri dispari devono ripetersi solo per un numero dispari di volte,
affinché venga rispettata la condizione di avere un'identità pitagorica estesa con tutti numeri interi.
Un esempio con un eptagono (poligono a 7 lati) dove ho usato numeri piccoli per far entrare la figura in un foglio, ma i numeri, tra pari e dispari, possono essere qualsiasi
le ipotenuse dei triangoli rettangoli consecutivi iniziano a "spiraleggiare".
un grazie a te, caro Andy, per la preziosa e continua collaborazione col "nostro" Circolo!