(QI) Cade o non cade ? **

04/11/22

(QI) Cade o non cade ? **

Categorie: Fisica classica Tags: Scritto da: Vincenzo Zappalà Commenti:8

QUI gli altri articoli dedicati all'attrito

 

Abbiamo introdotto l'attrito statico radente e siamo pronti a vederne un paio di applicazioni. Tuttavia, prima di iniziare, vi pongo una domanda che sembra banalissima (e forse lo è), a cui, però, viene normalmente risposto senza alcuna spiegazione fisica.

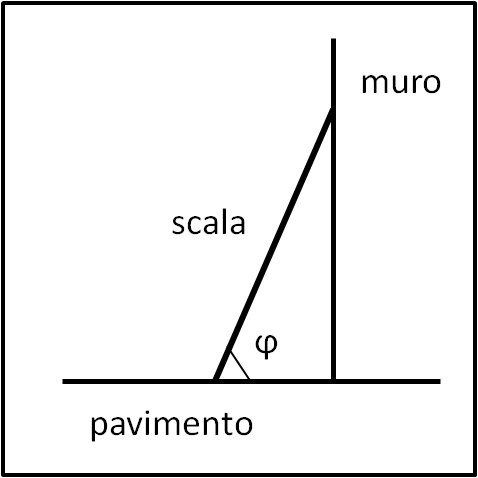
Immaginiamo che non esistano attriti. Poggiamo una scala di un certo peso P al muro con un certo angolo di inclinazione φ. La domanda è:

La scala sta ferma oppure no?

E perché (spiegazione fisica)?

Sembra un problema facilissimo, ma penso che possano nascere discussioni.

 

QUI la soluzione

Articoli correlati

8 commenti

  1. Leandro
    04/11/2022 at 20:45

    Semplifichiamo e supponiamo la scala su ruote, cioe con attrito volvente. Provate a salire sulla scala e avrete la soluzione.

  2. Vincenzo Zappalà
    05/11/2022 at 07:48

    L'esempio è calzante, ma perché cade? Che forze entrano in gioco?

  3. michele celenza
    05/11/2022 at 08:20

    Secondo me il problema va trattato considerando la scala un asta rigida nel cui baricentro è applicata la forza peso,  le forze in gioco sono la forza peso e le reazioni dei vincoli (nei punti di appoggio in alto e in basso).

    non essendo presente attrito le componenti delle reazioni vincolari nei punti di appoggio sono solo quelle normali alle superfici di appoggio nella parete verticale e nella base.

    Per avere l'equilibrio dell'asta si debbono verificare due condizioni:

    la somma delle forze agenti deve essere nulla

    la somma dei momenti delle forze rispetto ad un punto scelto ad arbitrio nel piano di riferimento deve essere nulla.

    le reazioni dei vicoli nei punti di appoggio hanno una componente parallela alle superfici ed una normale.

    nell'appoggio in alto la componente parallela non viene equilibrata dalla forza di attrito che non esiste e stesso vale per l'appoggio in basso.

    pertanto negli appoggi la componente  normale della forza peso viene equilibrata dalle reazioni normali e non vi è l'equilibrio per le componenti parallele.

    la scala (o asta) scivola in basso sula parete verticale e scivola a sx sulla base.

    pertanto la somma delle forze applicate non è nulla e stesso vale per la somma dei momenti

  4. Vincenzo Zappalà
    05/11/2022 at 10:46

    caro Michele,

    il tuo ragionamento fila fino a un certo punto. Poi mi sembra poco chiaro... Tu dici:

    le reazioni dei vicoli nei punti di appoggio hanno una componente parallela alle superfici ed una normale.

    Le reazioni dei vincoli NON hanno una componente parallela alle superfici

    pertanto negli appoggi la componente  normale della forza peso viene equilibrata dalle reazioni normali e non vi è l'equilibrio per le componenti parallele.

    Le componenti parallele non esistono

    Potresti chiarire meglio il tuo pensiero, magari con una figura (Daniela ti aiuterà a inserirla nel commento)?

  5. michele celenza
    05/11/2022 at 14:04

    Si avendo per ipotesi supposto nullo l'attrito sui vincoli sono presenti solo le reazioni normali.

     

  6. Fabrizio
    05/11/2022 at 14:16

    Mi inserisco con la mia risposta probabilmente fuori tema, ma che mi permette di sfruttare questa occasione per applicare ancora il metodo di Lagrange.

    Questo metodo, in questo caso ha il vantaggio di evitare ragionamenti sulle forze di reazione e come applicarle. Ragionamenti diversi caso per caso e non semplici come i commenti precedenti  mi sembra dimostrino. Richiede di fare qualche derivata, ma segue una procedura abbastanza standard.

    Gradi di libertà del problema e scelta delle coordinate

    La configurazione della scala ha un solo grado di libertà, quindi mi serve una sola coordinata per descriverla. E’ vero che la scala si muove in verticale, orizzontale e perfino ruota, ma ogni sua posizione è completamente determinata dall’angolo \varphi della figura. Quindi scelgo questa grandezza \varphi come coordinata.

    Nota: potrei scegliere anche altre, ad esempio l’altezza del baricentro della scala. Si possono fare dei tentativi per trovare la coordinata che rende meno complicata la risoluzione del problema. Per quanto ho visto \varphi sembra la più semplice da utilizzare.

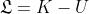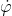    La funzione Lagrangiana è data dalla differenza tra energia cinetica, K, ed energia potenziale, U: \mathfrak{L}=K-U. Dovo calcolare i due termini K ed U in funzione di \varphi e della sua derivata rispetto al tempo \dot{\varphi}.

    Calcolo dell'energia cinetica

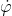    Sposto l’attenzione sul baricentro della scala che suppongo essere al centro della scala. Per calcolare l’energia cinetica devo conoscere l’espressione del quadrato della velocità del baricentro come funzione di \varphi e della sua derivata rispetto al tempo \dot{\varphi}.

    Parto dalla posizione del baricentro  in coordinate cartesiane (x,y) che esprimo in funzione di \varphi:

    x=-\frac{l}{2} \cos(\varphi)   e     y=\frac{l}{2} \sin(\varphi)     dove con l ho indicato la lunghezza della scala.

    La velocità è la derivata rispetto al tempo della posizione. Faccio le derivate rispetto al tempo delle due coordinate cartesiene:

    \dot{x}=-\frac{l}{2}\frac{d \cos(\varphi)}{dt}=\frac{l}{2} \sin(\varphi) \dot{\varphi}      e        \dot{y}=\frac{l}{2} \cos(\varphi)\dot{\varphi}

    Solo \varphi è funzione del tempo e si trova all'interno di un'altra funzione. Quindi ho applicato la regola di derivazione delle funzioni composte \frac{df(\varphi)}{dt}=\frac{df(\varphi)}{d\varphi}\frac{d\varphi}{dt}

    Queste due componenti della velocità sono perpendicolari tra loro. Posso applicare il teorema di Pitagora per trovare il quadrato della loro risultante:

    \small v^2=\dot{x}^2+\dot{y}^2=\left(\frac{l}{2} \sin(\varphi) \dot{\varphi} \right)^2+\left(\frac{l}{2} \cos(\varphi)\dot{\varphi}\right)^2=\frac{l^2}{4} \left(\sin(\varphi)^2+\cos(\varphi)^2\right) \dot{\varphi}^2

    v^2=\frac{l^2}{4} \dot{\varphi}^2

    Quindi l’energia cinetica dovuta al moto del baricentro è data da:

    \frac{l}{2}m v^2= \frac{l^2}{8} m \dot{\varphi}^2            dove m è la massa della scala.

    Ora c’è una complicazione che evito. La scala ha anche un movimento di rotazione, scorrendo non si mantiene parallela. Dovrei tenere conto anche dell’energia associata a questo movimento. Evito questa complicazione pensando tutto il peso della scala concentrato nel baricentro.

    Calcolo dell'energia potenziale

    L’energia potenziale gravitazionale ha la solita espressione:

    U=m g y=m g \frac{l}{2} \sin(\varphi)

    Calcolo della Lagrangiana

    Con l'energia cinetica e l'energia potenziale posso comporre l’espressione della Lagrangiana:

    \mathfrak{L}=K-U=\frac{l^2}{8} m \dot{\varphi}^2-m g \frac{l}{2} \sin(\varphi)

    Applicazione della equazione di Eulero-Lagrange

    Dalla Lagrangiana si può ottenere l’accelerazione di 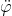\varphi, \ddot{\varphi}, applicando l’equazione di Eulero – Lagrange:

    {\color{DarkGreen} \frac{d}{dt}}{\color{Red} \frac{\partial \mathfrak{L}}{\partial \dot{\varphi}}}-{\color{Blue} {\color{DarkBlue} }\frac{\partial \mathfrak{L}}{\partial \varphi}}=0

    Colcolo separatamente ciascun termine.

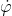    {\color{Red} \frac{\partial \mathfrak{L}}{\partial \dot{\varphi}}}=\frac{l^2}{8} m \frac{\partial}{\partial \dot{\varphi}}\dot{\varphi}^2=\frac{l^2}{8} m 2\dot{\varphi}=\frac{l^2}{4} m \dot{\varphi}

    poiché \dot{\varphi} è presente solo nel primo termine della Lagrangiana e la derivata di una generica variabile w al quadrato e 2w.

    Segue che:

    {\color{DarkGreen} \frac{d}{dt}}{\color{Red} \frac{\partial \mathfrak{L}}{\partial \dot{\varphi}}}={\color{Red} \frac{l^2}{4} m \frac{{\color{DarkGreen} d} \dot{\varphi}}{{\color{DarkGreen} dt}}}=\frac{l^2}{4} m \ddot{\varphi}         poichè solo \dot{\varphi} dipende dal tempo.

    Passo al secondo termine dell’equazione che sviluppo in questo modo:

    {\color{Blue} \frac{\partial \mathfrak{L}}{\partial \varphi}}=-m g \frac{l}{2} \frac{\partial \sin(\varphi)}{\partial \varphi}=-m g \frac{l}{2} \cos(\varphi)

    poichè \varphi è presente solo nel secondo termine della Lagrangiana dove solo \sin(\varphi) dipende da \varphi.

    Mettendo nell'equazione di Eulero-Lagrange i due termini che sviluppati ed  ottengo che:

    \frac{l^2}{4} m \ddot{\varphi}+m g \frac{l}{2} \cos(\varphi)=0

    Da qui posso isolare l’accelerazione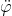 \ddot{\varphi} portando tutti gli altri termini a sinistra:

    \ddot{\varphi}=-\frac{4}{l^2}\frac{1}{m} m g \frac{l}{2} \cos(\varphi)=-g \frac{2}{l} \cos(\varphi)

    \boldsymbol{\ddot{\varphi}} è sempre negativa con  0\leq \varphi< 90^{o}. Quindi, appoggiando la scala al muro, l'angolo \varphi tenderebbe via via a diminuire, cioè la scala cade.

    Considerando anche l'energia di rotazione della scala il risultato è solo di poco diverso ed il metodo per otterlo lo stesso;

    \ddot{\varphi}=-g \frac{3}{2\,l} \cos(\varphi). L'accelerazione è di 1/4 minore, intuitivamente perché parte dell'energia potenziale è "assorbita" dall'energia di rotazione.

    Se non ho fatto errori, questo è il risultato che vi sottopongo.

  7. Vincenzo Zappalà
    05/11/2022 at 17:28

    Caro Fabrizio,

    la tua è una spiegazione ineccepibile, ma io pretendevo molto meno per esercitarsi sugli attriti... Non è difficile vedere che la scala non è in equilibrio giocando solo sulle forze applicate alla scala. Adesso pubblico la "mia" soluzione semplificata (statica), ma ti inviterei a pubblicare separatamente anche la tua che è essenzialmente un problema di dinamica.

  8. Gianfranco
    05/11/2022 at 19:13

    Con la scala inclinata, quindi l’angolo < 90°, la forza peso considerata nel baricentro, genera un momento rispetto alla base, che viene contrastato dalla forza orizzontale nel punto di appoggio sul muro.

    Questa forza non trova il vincolo dell’attrito ma semplice appoggio alla base labile.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.