Categorie: Fisica classica
Tags: attrito attrito radente equazioni cardinali equilibrio statico imbianchino scala
Scritto da: Vincenzo Zappalà
Commenti:21
(QI) L'imbianchino non cade, se ... ***
QUI gli altri articoli dedicati all'attrito
Ecco la soluzione relativa al problema della scala e dell'imbianchino...
Innanzitutto facciamo un paio di premesse...
(1) Il problema non solo è risolvibile, ma viene anche fornito un dato in più del necessario. Infatti, la soluzione è indipendente dal peso dell'imbianchino. Ovviamente, ipotizzando che la scala non solo sia rigida ma indistruttibile per qualsiasi carico, altrimenti il problema non sarebbe più soltanto di equilibrio statico.
(2) Trascurare il peso della scala è del tutto ininfluente, in quanto potrei sempre sommare la forza peso della scala con quella dell'imbianchino e tradurla in unica forza verticale.
Disegniamo il sistema evidenziando le forze che agiscono sulla scala.

I dati che conosciamo sono L, a e il coefficiente d'attrito del pavimento e del muro μ, mentre vogliamo calcolare x, necessario all'equilibrio. La scala ha come peso solo quello dell'imbianchino che poniamo nel punto I. In A e B sono presenti due forze vincolari (NA e NB) che sono rispettivamente perpendicolari al pavimento e al muro. In A e B giocano anche le forze di attrito FA e FB che sono perpendicolari alle forze vincolari. Il loro verso è quello che va in verso opposto al movimento della scala che vogliamo evitare, ossia FA è diretta verso sinistra e FB verso l'alto, dato che la scala tende a scivolare sul pavimento verso destra e sul muro verso il basso (vedi articolo precedente). Non vi sono altre forze in gioco.
Per definizione di forza d'attrito, sappiamo che possiamo scrivere le seguenti due relazioni:
FB = μ NB .... (1)
FA = μ NA .... (2)
Applichiamo la prima equazione cardinale (annullamento delle forze), limitandoci alle componenti orizzontali.
FA = NB .... (3)
Passiamo poi alle componenti verticali
FB + NA = P .... (4)
Le (3) e le (4) ci danno i moduli delle forze (NB ha verso contrario di FA e FB e NA verso contrario di P).
La (2) e la (3) comportano che:
NB = FA = μ NA
NA = NB/μ
La (4) diventa, ricordando la (1):
μNB + NB/μ = P
NB(μ + 1/μ) = P
NB(μ2 + 1)/μ = P
NB = P μ/( μ2 + 1) .... (5)
Passiamo, adesso, alla seconda equazione cardinale (annullamento dei momenti), prendendo con punto di riferimento A, in modo che si annullino subito due momenti (quello di NA e quello di FA) dato che il loro braccio risulta uguale a zero.
Abbiamo tre forze che causano un momento, di cui due in verso orario (FB e NB) e una in verso antiorario (P). Ne segue che la somma dei primi due moduli deve essere uguale al modulo della terza, ossia:
FB L cos a + NB L sin a = P x cos a .... (6)
Ricordando la (1) inserisco μ NB al posto di FB:
μ NB L cosa a + NB L sin a = P x cos a
NB L (μ cos a + sin a) = P x cos a
Ricordando la (5) scrivo NB in funzione di P e di μ:
P (μ/( μ2 + 1)) L (μ cos a + sin a) = P x cos a
Ed ecco che, come per magia, sparisce la forza peso dell'imbianchino...
(μ/( μ2 + 1)) L (μ cos a + sin a) = x cos a
L'unica incognita rimane x
x = L (μ/( μ2 + 1)) (μ cos a + sin a)/cos a .... (7)
x = 5 (0.35/(0.35 2 + 1))(0.35 · cos 60° + sin 60°)/cos 30°
x ∼ 5 · 0.31 (0.35 · 0.5 + 0.87)/0.5 = 3. 24
x ∼ 3.24
L'imbianchino può salire solo fino a 3.24 m lungo la scala, altrimenti l'equilibrio salta e la scala scivola con l'imbianchino: Einstein scopre la Relatività Generale!
Cosa deve fare l'imbianchino per salire fino alla cima della scala? Beh... basta prendere la (7) e porre x = L. L'unica incognita risulta essere l'angolo a.
L = L (μ/( μ2 + 1)) (μ cos a + sin a)/cos a
1 = (μ/( μ2 + 1)) (μ cos a + sin a)/cos a
1 = μ(μ + tan a)/( μ2 + 1)
μ2 + 1 = μ2 + μ tan a
tan a = 1/μ
a ∼ 70.7 °
E torniamo a Newton...
Cesco ha conservato la forza peso, ma è comunque arrivato al risultato: bravo! Peccato che il suo commento non sia facile da leggere...
QUI il quiz






21 commenti
In ogni caso, l'attrito è una gran cosa, senza di lui non potremmo nemmeno camminare.
Non dirlo, però, a chi deve spostare una pietra per costruire le piramidi...
Non mi ritrovo nella soluzione descritta sopra. Di seguito cerco di spiegare le regioni.
Le relazioni (1) e (2) sono delle disuguaglianze: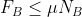 e
e 
Le uguaglianze sono quelle delle equazioni della statica. Le uguaglianze che bilanciano le forze di reazione e d’attrito, fino a che è possibile, con le forze attive. Nel nostro caso:
A queste si aggiunge l’uguaglianza dei momenti, che qui scelgo di prendere rispetto al punto A:
caro Fabry,
le relazioni 1 e 2 sono delle uguaglianze se si vuole cercare il valore massimo dell'attrito per non iniziare a scivolare. E' ovvio che se siamo in condizioni più favorevoli tutto va bene, ma si chiede il valore massimo dell'attrito che faccia rimanere tutto in equilibrio.
Le 1 e 2 sono uguaglianze nelle condizioni limite dell'equilibrio, Esse permettono di legare tra di loro col segno di uguale due forze con l'aiuto del coefficiente massimo d'attrito. Oltre esso non può andare e quindi la scala cade...
Non riusciamo a spiegarci... comunque, non sono il solo a vederla così...
Più la forza impressa é grande e più aumenta la forza d'attrito che continua a controbilanciare (e quindi annullare) la forza impressa. In poche parole, il corpo riesce a rimanere fermo, in equilibrio statico. A un certo punto, però, l'attrito raggiunge il suo valore massimo e se la forza riesce a superarlo inizia il movimento e si perde l'equilibrio statico. Questo succede proprio quando F =μN
Vediamo di dirla in un altro modo...
Se cambio la forza peso dell'imbianchino, cambia automaticamente la forza di attrito massima, ma ciò non toglie che la soluzione sia indipendente dai valori assunti, dato che ciò che conta è proprio l'uguaglianza tra la forza esterna e il valore massimo dell'attrito: cresce una e cresce anche la reazione vincolare e quindi l'attrito massimo, a parità di coefficiente. Questa uguaglianza fa sì che la configurazione geometrica dell'equilibrio non cambi. Stiamo, ovviamente, parlando di LIMITE per l'equilibrio.
Non so proprio come spiegarmi meglio... L'uguaglianza tra FA e NB è fondamentale ed essa si verifica imponendo l'equilibrio, qualsiasi sia la forza esterna. Ma anche l'uguaglianza tra FA e µNA è fondamentale, dato che abbiamo bisogno dell'attrito massimo.
Caro Enzo,
quello che dici nella tua risposta non contraddice il mio commento.
Mi sembra che stiamo dicendo che abbiamo un modello della nostra scala, le equazioni e le diseguaglianze della statica. Applicate al nostro caso consistono in 4 forze, 3 equazioni e 2 disuguaglianze. (Nel modello ci sono anche 3 parametri: la posizione dell’imbianchino, il suo peso e l’inclinazione della scala.)
Una configurazione delle 4 forze è di equilibrio se soddisfa le 3 equazioni e le 2 disuguaglianze.
Inoltre abbiamo un metodo, che almeno in questo caso, ci dice quale è tra tutte le configurazioni di equilibrio possibili quella con l’imbianchino posizionato più in alto. Le 2 disuguaglianze diventano uguaglianze, abbiamo 5 equazioni e 5 incognite (le 4 forze e la posizione dell’imbianchino che da parametro diventa incognita). Ho riportato i valori che si ottengono per le 4 forze nel commento precedente.
Per la posizione più elevata dell’imbianchino potenzialmente di equilibrio, oltre alla configurazione di equilibrio delle forze ce ne sono infinite altre compatibili con le 3 equazioni della statica che non sono di equilibrio perché non soddisfano almeno una delle disuguaglianze. Una di queste l’ho riportata nel mio commento precedente.
Credo che fino a qui siamo d’accordo. La differenza è nelle conclusioni che ne traiamo.
Io mi allineo con chi pensa che il nostro modello non ci permetta di indicare tra tutte le possibili configurazioni compatibili con le 3 equazioni della statica quale sarà quella che assumerà il sistema e quindi non possiamo affermare se la scala cadrà o non cadrà. Per arrivare ad una decisione occorre trattare il problema con un modello più complesso.
Mi sembra che nella tua soluzione si faccia fare un passo ulteriore al modello assumendo che se ci sono diverse configurazioni compatibili con le equazioni della statica, una (o alcune) di equilibrio ed altre non, il sistema assumerà quella di equilibrio. Quindi, da quanto detto sopra se ne trae che la scala con l’imbianchino posizionato all’altezza trovata sopra non solo è potenzialmente in equilibrio, ma è proprio in equilibrio.
L’unica via per risolvere la questione sarebbe una sperimentazione.
Chi fa l’imbianchino?
Cominciamo a concordare...
Resta il fatto che il problema non chiede di determinare il valore delle forze, ma solo la configurazione limite di equilibrio. D'altra parte, dimmi cosa c'è di sbagliato nell'approccio che ho riportato? L'equazione che dice che l'attrito è una forza moltiplicata per un certo coefficiente è un dato di fatto, così come l'uguaglianza tra attrito e forza applicata, trattandosi di "momento del distacco". Quella che tu dai come un'altra soluzione va contro la definizione di attrito massimo, dato che FA è diverso da nu moltiplicato NA. Questa situazione è quella che andrebbe contro natura, dato che cambierebbe la realtà dell'attrito statico. Mi sembra automatico che questa configurazione è proprio l'unica che rappresenti il limite di movimento. Certo è che se cambi l'equazione dell'attrito, tutto può succedere, ma non è quello che capita in Natura. Qualsiasi altra soluzione va in un verso o nell'altro. Se vale il segno "inferiore" la scala è sicuramente in equilibrio, ma se vale il segno > si va contro Natura e l'attrito non sarebbe quello massimo. Infatti, il peso non conta, poiché, se lui cambiasse, cambierebbero anche le forze normali e anche gli attriti massimi: sono tutte e tre collegate tra loro quando si è nelle condizioni limite. Io continuo a vederla così...
Cerco di spiegarmi ancora meglio...
In partica, data la forza peso vengono anche date le relazioni tra reazioni e attriti. Dato anche il coefficiente, rimane come incognita solo l'angolo della scala. In altre parole, qualsiasi sia il peso si ottiene l'equilibrio che dipende soltanto dall'angolo. Se cresce la reazione cresce automaticamente l'attrito massimo (ossia più spingo verso il basso e maggiore è l'attrito, capace sempre di mantenere l'equilibrio). Si può anche pensare così: variando la posizione dell'imbianchino, le forze continuano ad annullarsi tra loro, ma i momenti cambiano i loro bracci e, a un certo punto, non si equilibrano più.
L'equivoco è nato dal fatto che "al limite" FB =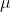 NB
NB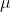 NA , basta che sia FA<
NA , basta che sia FA< 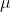 NA
NA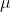 <1 .
<1 .
Ma questo non implica che FA =
in ogni caso NB=FB <FA perché
E infatti...
NB = FA = μ NA
Non riesco a capire le critiche a riguardo...
Mi sembra che un punto sul quale divergiamo sia il modo di considerare le configurazioni delle 4 forze non compatibili con le disuguaglianze. Provo a chiarire la mia posizione che, almeno in parte, risponde alle tue ultime osservazioni.
Per spiegare la ragione per la quale credo si debbano considerare anche le configurazioni delle 4 forze non di equilibrio, propongo di esaminare il caso di una scala senza attrito sul muro. In questo caso le forze incognite sono 3, anche le equazioni sono 3 e rimane la sola disuguaglianza relativa ad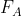 .
.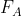 soddisfa la disuguaglianza
soddisfa la disuguaglianza 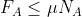 .
.
Per ogni configurazione dei parametri posizione dell'imbianchino, inclinazione della scala e peso dell'imbianchino corrisponde una configurazione delle tre forze compatibile con le 3 equazioni. In alcune di queste
Ad esempio per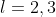 e
e 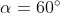 , dalle 3 equazioni della statica ricavo che le 3 forze dovrebbero avere questi valori:
, dalle 3 equazioni della statica ricavo che le 3 forze dovrebbero avere questi valori: 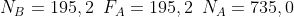 . Poiché
. Poiché 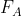 è minore di
è minore di 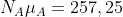 questa configurazione si può realizzare. Da qui possiamo affermare che la scala non cade, almeno per il nostro modello.
questa configurazione si può realizzare. Da qui possiamo affermare che la scala non cade, almeno per il nostro modello.
Per altri valori dei parametri, la configurazione compatibile con le 3 equazioni della statica contiene un valore di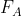 che non soddisfa la disuguaglianza
che non soddisfa la disuguaglianza 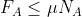 .
.
Ad esempio per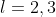 e
e 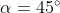 , dalle 3 equazioni della statica ricavo che le 3 forze dovrebbero avere questi valori:
, dalle 3 equazioni della statica ricavo che le 3 forze dovrebbero avere questi valori: 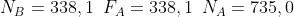 . In questo caso il valore di
. In questo caso il valore di 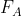 è maggiore di
è maggiore di 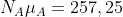 .
.
E' vero che questa configurazione non si può realizzare, ma proprio per questo possiamo affermare che la scala cade. Quindi non ignoro o scarto questi casi, ma li utilizzo per valutare la staticità della configurazione. Credo si possa dire che la fisica della scala genera le due forze normali, ma l'attrito non risponde adeguatamente e la scala inizia a scivolare. Lo scivolameneto porta il sistema a situazioni ancora più favorevoli alla caduta che quindi prosegue fino a terra.
Ora provo a fare un ragionamento parallelo in presenza di un muro con attrito. Abbiamo 4 forze incognite, 3 equazioni della statica e 2 disuguaglianze che limitano i valori di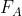 ed
ed 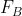 .
.
Prendo la prima configurazione di parametri vista sopra: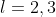 e
e 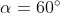 . Cerco la configurazione delle 4 forze compatibile con le 3 equazioni della statica. Questa volta ce ne sono infinite. Alcune presentano valori
. Cerco la configurazione delle 4 forze compatibile con le 3 equazioni della statica. Questa volta ce ne sono infinite. Alcune presentano valori 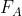 ed
ed 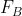 nei limiti delle rispettive disuguaglianze, altre nelle quali almeno una delle disuguaglianze fallisce.
nei limiti delle rispettive disuguaglianze, altre nelle quali almeno una delle disuguaglianze fallisce.
Ad esempio, questa configurazione delle 4 forze compatibile con le 3 equazioni della statica
![\left [ N_{A} = 680,0\; \; N_{B} = 163,45\; \; F_{A} = 163,45\; \; F_{B} = 55,0 \right ]](http://latex.codecogs.com/gif.latex?\left&space;[&space;N_{A}&space;=&space;680,0\;&space;\;&space;N_{B}&space;=&space;163,45\;&space;\;&space;F_{A}&space;=&space;163,45\;&space;\;&space;F_{B}&space;=&space;55,0&space;\right&space;]) e soddisfa anche le due disuguaglianze poiché
e soddisfa anche le due disuguaglianze poiché
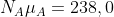 e
e 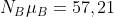 .
.
Ma anche questa altra configurazione delle 4 forze è compatibile con le 3 equazioni della statica![\left [ N_{A} = 670,0\; \; N_{B} = 157,67\; \; F_{A} = 157,67\; \; F_{B} = 65,0\: \right ]](http://latex.codecogs.com/gif.latex?\left&space;[&space;N_{A}&space;=&space;670,0\;&space;\;&space;N_{B}&space;=&space;157,67\;&space;\;&space;F_{A}&space;=&space;157,67\;&space;\;&space;F_{B}&space;=&space;65,0\:&space;\right&space;]) , ma non soddisfa una delle disuguaglianze poiché
, ma non soddisfa una delle disuguaglianze poiché 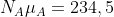 e
e 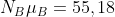
Nel caso con muro liscio per casi come il primo abbiamo tratto la conclusione che la scala non sarebbe caduta, per casi come il secondo abbiamo tratto la conclusione che la scala sarebbe caduta.
In questo caso abbiamo risultati contraddittori poiché per la stessa situazione sono compatibili con le 3 equazioni della statica sia configurazione delle 4 forze che soddisfano le disuguaglianze sia che non le soddisfano.
Non vedo neanche il perché, in base al modello utilizzato, si possa dire che si verificano solo le situazioni di equilibrio. Per il caso di muro liscio abbiamo detto che le altre situazioni esistono e si manifestano con la caduta della scala per l'insufficienza della forza di attrito.
Per questo penso che sia corretta la posizione di chi afferma che il modello di scala che utilizziamo e le sole equazioni e disuguaglianze della statica non riescano a determinare un risultato in questo caso di muro con attrito.
non riesco a capire... Noi abbiamo chiesto il valore limite dell'altezza dell'imbianchino... non abbiamo chiesto quanto valgono le forze in gioco. Per valori superiori la scala cade e per valori inferiori non cade. Ma, ripeto, a noi serve il valore limite di ascesa.
Indubbiamente una configurazione di forze di attrito limite, con le due disuguagliane trasformate in uguaglianze, comporta il valore per x di circa 3,24.
Considerando che la relazione tra x e la configurazione di forze non è biunivovìca come nel caso senza attrito sul muro, la domanda che mi sono fatto è questa:
una valore di x=3,24, cioè ponendo l'imbianchino nella posizione x=3,24, è sicuro che porti alla configurazione limite di equilibrio?
Sostanzialmente il ragionamento sulle forze che ho fatto nei miei commenti serviva ad evidenziare che la relazione non è biunivoca e che, per questo, il modello utilizzato non mi sembra dia la risposta alla domanda.
Nota per eventuali lettori che volessero un esempio semplice di relazione non biunivoca.
Se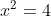 e noto che
e noto che ^2=4) non posso concludere con certezza che
non posso concludere con certezza che 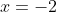 .
.
Per agganciare meglio la mia risposta al tuo ultimo commento faccio una aggiunta.
Se non posso rispondere alla domanda fatta sopra: una valore di x=3,24, cioè ponendo l'imbianchino nella posizione x=3,24, è sicuro che porti alla configurazione limite di equilibrio?
non posso neanche affermare che x=3,24 sia il valore limite dell'altezza dell'imbianchino
( intendendo per valore limite dell'altezza dell'imbianchino il punto x massimo nel quale si può porre l'imbianchino senza far cadere la scala).
Continuo non capire la non univocità... Se salgo di più cado sicuramente. Ovviamente è valida qualsiasi soluzione con un'ascesa più corta. Ripeto: dov'è l'errore nella trattazione. Segnami la relazione che ti dà problemi. Poi smettiamo pure, altrimenti non ne usciamo vivi... Non fare esempi numerici, ma dimmi esattamente cosa non va bene nelle equazioni che ho scritto. Ovviamente, devi accettare la definizione di attrito massimo...
Tanto per dimostrare che non sono il solo a pensarla così...
https://www.youtube.com/watch?v=vtpE5synod8
Se mi chiedi dove è l'errore nella tua trattazione, la mia risposta è che non c'è alcun errore. Il problema, a mio parere, è che assume troppo presto che il valore di x trovato sia il valore max di x sul quale si può porre l'imbianchino senza far cadere la scala.
Provo ad evidenziare il punto dove divergiamo seguendo il procedimento in parallelo per il caso senza e con attrito sul muro.
Considero dimostrato che assegnando alle forze di attrito il loro valore limite massimo posso ottenere il valore di x più elevato (che chiamo ) corrispondente a una configurazione delle forze di reazione ed attrito di equilibro. Per il caso senza attrito sul muro si tratta di una tripletta di forze [
) corrispondente a una configurazione delle forze di reazione ed attrito di equilibro. Per il caso senza attrito sul muro si tratta di una tripletta di forze [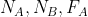 ] . Nel caso di muro con attrito si tratta di una quadrupletta di forze, [
] . Nel caso di muro con attrito si tratta di una quadrupletta di forze, [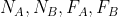 ].
].
Muro senza attrito
Muro con attrito
Condizioni attrito limite

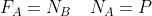
=L&space;N_B&space;\sin(\alpha))
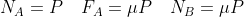
)
Equazioni della statica
Dalle prime 3 equazioni ricavo che:
inserendole nell’ultima equazione ricavo:
Condizioni attrito limite

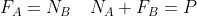
=L&space;\left&space;(&space;N_B&space;\sin(\alpha)+&space;F_B&space;\cos(\alpha)&space;\right&space;))
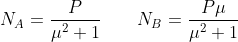
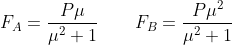
+&space;\mu&space;\right&space;))
Equazioni della statica
Dalle prime 4 equazioni ricavo che:
inserendole nell’ultima equazione ricavo
A questo punto sembrerebbe che abbiamo ottenuto il risultato cercato: è quello che cercavamo.
è quello che cercavamo.
Qui mi differenzio.
Io propongo di fare la ‘prova del 9’. Intendo dire, se inseriamo il valore di trovato nelle equazioni della statica dovremmo ottenere la configurazione di forze di reazione ed attrito dalla quale siamo partiti o almeno una configurazione di equilibrio.
trovato nelle equazioni della statica dovremmo ottenere la configurazione di forze di reazione ed attrito dalla quale siamo partiti o almeno una configurazione di equilibrio.
In fin dei conti il quesito è proprio questo. Quale è il valore massimo di x nel quale si può porre l’imbianchino senza far cadere la scala?
Allora mettiamo idealmente nel nostro modello l’imbianchino in e vediamo se otteniamo una configurazione di equilibrio.
e vediamo se otteniamo una configurazione di equilibrio.
Muro senza attrito
Muro con attrito
Equazioni della statica
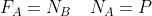
con
da cui:
ed ottengo che:
che coincide esattamente con la tripletta di forze trovata sopra che, per come l'abbiamo definita, è certamente di equilibrio.
Il modello che utilizziamo mi conferma che se l'imbianchino si posiziona in
Equazioni della statica
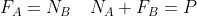
=L&space;\left&space;(&space;N_B&space;\sin(\alpha)+&space;F_B&space;\cos(\alpha)&space;\right&space;))
+&space;\mu&space;\right&space;))
 .
. la scala cade o non cade? Di conseguenza non sappiamo dire se
la scala cade o non cade? Di conseguenza non sappiamo dire se  sia la posizione più alta sulla quale si può porre l'imbianchino senza far cadere la scala.
sia la posizione più alta sulla quale si può porre l'imbianchino senza far cadere la scala.
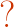
con
Abbiamo 3 equazioni e 4 incognite.
Il modello non può rispondere in modo univico.
Al più possiamo esprimere parametricamente le infinite quadruplette di forze compatibili con
Se le analizziamo queste infinite quadruplette di forze, troveremmo che solo una è di equilibrio, quella dalla quale siamo partiti sopra. Le altre porterebbero alla caduta della scala.
Io concludo che in questo caso con il nostro modello non ci permette di rispondere alla domanda: se l'imbianchino si pone nella posizione
Purtroppo la formattazione delle tabelle non ha funzionato. Non credo si riesca a capire a quale caso si riferiscono le espressioni scritte sopra. Riscrivo il tutto senza usare le tabelle.
Se mi chiedi dove è l'errore nella tua trattazione, la mia risposta è che non c'è alcun errore. Il problema, a mio parere, è che assume troppo presto che il valore di x trovato sia il valore max di x sul quale si può porre l'imbianchino senza far cadere la scala.
Provo ad evidenziare il punto dove divergiamo seguendo il procedimento in parallelo per il caso senza e con attrito sul muro.
Considero dimostrato che assegnando alle forze di attrito il loro valore limite massimo posso ottenere il valore di x più elevato (che chiamo ) corrispondente a una configurazione delle forze di reazione ed attrito di equilibro. Per il caso senza attrito sul muro si tratta di una tripletta di forze [
) corrispondente a una configurazione delle forze di reazione ed attrito di equilibro. Per il caso senza attrito sul muro si tratta di una tripletta di forze [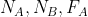 ] . Nel caso di muro con attrito si tratta di una quadrupletta di forze, [
] . Nel caso di muro con attrito si tratta di una quadrupletta di forze, [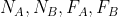 ].
].
Muro senza attrito
Condizioni attrito limite

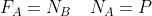
=L&space;N_B&space;\sin(\alpha))
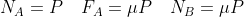
)
Equazioni della statica
Dalle prime 3 equazioni ricavo che:
inserendole nell’ultima equazione ricavo:
Muro con attrito
Condizioni attrito limite

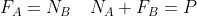
=L&space;\left&space;(&space;N_B&space;\sin(\alpha)+&space;F_B&space;\cos(\alpha)&space;\right&space;))
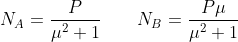
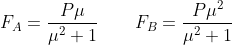
+&space;\mu&space;\right&space;))
Equazioni della statica
Dalle prime 4 equazioni ricavo che:
inserendole nell’ultima equazione ricavo
A questo punto sembrerebbe che abbiamo ottenuto il risultato cercato: è quello che cercavamo.
è quello che cercavamo.
Qui mi differenzio.
Io propongo di fare la ‘prova del 9’. Intendo dire, se inseriamo il valore di trovato nelle equazioni della statica dovremmo ottenere la configurazione di forze di reazione ed attrito dalla quale siamo partiti o almeno una configurazione di equilibrio.
trovato nelle equazioni della statica dovremmo ottenere la configurazione di forze di reazione ed attrito dalla quale siamo partiti o almeno una configurazione di equilibrio.
In fin dei conti il quesito è proprio questo. Quale è il valore massimo di x nel quale si può porre l’imbianchino senza far cadere la scala?
Allora mettiamo idealmente nel nostro modello l’imbianchino in e vediamo se otteniamo una configurazione di equilibrio.
e vediamo se otteniamo una configurazione di equilibrio.
Muro senza attrito
Equazioni della statica
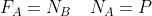
con
da cui:
ed ottengo che:
che coincide esattamente con la tripletta di forze trovata sopra che, per come l'abbiamo definita, è certamente di equilibrio.
Il modello che utilizziamo mi conferma che se l'imbianchino si posiziona in
Muro con attrito
Equazioni della statica
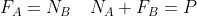
=L&space;\left&space;(&space;N_B&space;\sin(\alpha)+&space;F_B&space;\cos(\alpha)&space;\right&space;))
+&space;\mu&space;\right&space;))
con
Abbiamo 3 equazioni e 4 incognite. .
. la scala cade o non cade? Di conseguenza non sappiamo dire se
la scala cade o non cade? Di conseguenza non sappiamo dire se  sia la posizione più alta sulla quale si può porre l'imbianchino senza far cadere la scala.
sia la posizione più alta sulla quale si può porre l'imbianchino senza far cadere la scala.
Il modello non può rispondere in modo univoco.
Al più possiamo esprimere parametricamente le infinite quadruplette di forze compatibili con
Se le analizziamo queste infinite quadruplette di forze, troveremmo che solo una è di equilibrio, quella dalla quale siamo partiti sopra. Le altre porterebbero alla caduta della scala.
Io concludo che in questo caso con il nostro modello non ci permette di rispondere alla domanda: se l'imbianchino si pone nella posizione
Nel secondo caso manca una relazione:
FA = FB/μ
dato che
FA = μ NA
FB = μ NB
FA = NB
....
In questo modo assumi a priori che la soluzione richiederà il massimo attrito, nulla di più e nulla di meno.
Nel caso di muro senza attrito non viene fatta questa assunzione e sono le equazioni della statica ad indicare che la soluzione è di massimo attrito.
Comunque, credo che facciamo riferimento a due modelli diversi. Danno lo stesso risultato quando le 3 equazioni della statica forniscono una unica soluzione. Divergono a causa della diversa interpretazione delle disuguaglianze quando le forze incognite sono più di 3, cioè le 3 equazioni non danno un risultato univoco.
A mio parere le disuguaglianze servono a discriminare le soluzioni fornite dalle 3 equazioni tra quelle di equilibrio e quelle che non consentono l'equilibrio. Questo mi porta a considerare il risultato indeterminato quando tra le soluzioni ce ne sono dei due tipi.
Interpretando i tuoi commenti, capisco che nel modello al quale fai riferimento le disuguaglianze selezionano le soluzioni in generale. Quindi basta che tra soluzioni compatibili con le 3 equazioni della statica ce ne sia almeno una di equilibrio il sistema viene considerato in equilibrio poiché quelle non compatibili con le diseguaglianze vengono scartate dalle diseguaglianze.
Io propendo per la prima interpretazione, ma non posso escludere la seconda.
Io rimango convinto che dati a,µ,P la soluzione sia unica. Non ci resta, veramente, che trovare un imbianchino che voglia fare la prova e salire un po' più in alto...