Categorie: Matematica
Tags: studentesse liceali teorema di Pitagora trigonometria
Scritto da: Vincenzo Zappalà
Commenti:5
Quando la matematica diventa arte ***/*****
La matematica continua a essere considerata fredda e ripetitiva. Niente di più sbagliato. In certi casi può diventare un'opera d'arte e, come tale, non ha nemmeno bisogno di essere veramente utile. L'importante è che meravigli e faccia pensare...
In questo articolo vogliamo parlare di Calcea Johnson e Ne'Kiya Jackson, della St. Mary's Academy di New Orleans, due studentesse liceali (di un bellissimo colore nero della pelle) che hanno presentato, lo scorso marzo, una nuova dimostrazione del teorema di Pitagora basata sulla trigonometria. Esistono più di 370 dimostrazioni del teorema, forse il più celebre in assoluto, ma nessuna si è mai realmente basata sulla trigonometria o, almeno, non in modo così limpido e ingegnoso.

Il problema di tale dimostrazione è che il Teorema di Pitagora è equivalente all’identità fondamentale della trigonometria, che afferma che la somma tra il seno al quadrato di un angolo e il coseno al quadrato dello stesso angolo è pari a uno. La stragrande maggioranza delle relazioni trigonometriche discende da questa e sembrava impossibile usare relazioni trigonometriche che fossero “immuni” da questa identità. In poche parole, la trigonometria sembrava poter dimostrare il teorema solo partendo dal teorema stesso, un gatto che si morde la coda.
Sono veramente rare le espressioni trigonometriche "immuni". Tra queste il teorema dei seni e, ovviamente, la definizione di seno e coseno.
L'approccio usato dalle due studentesse è perfetto, anche se non fa solo uso della trigonometria, ma anche dell'algebra. Resta, comunque, un piccolo capolavoro. Come già detto, probabilmente non serve a niente di pratico, dato che il teorema è ampiamente dimostrato, ma neanche un'opera d'arte, in fondo, serve a qualcosa, tranne che a stupire e a far subire emozioni forti e "belle"... sappiamo bene quanto ve ne sia bisogno nello squallido mondo odierno.
Cominciamo , ovviamente, da un triangolo rettangolo, i cui lati, in ordine di lunghezza sono chiamati a, b e c. Analogamente chiamiamo α, β, e γ= 90° gli angoli opposti ai tre lati. Disegniamolo in Fig. 1.
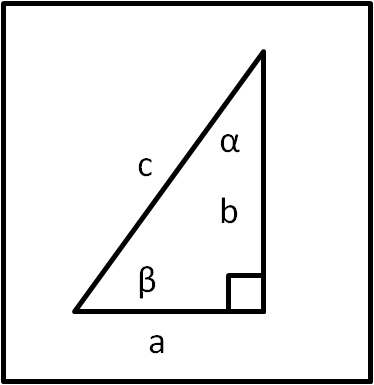
La prima cosa da fare è scrivere una relazione trigonometrica in cui compaia il quadrato dell'ipotenusa c e che non faccia ovviamente uso dell'identità trigonometrica. Niente di meglio che partire dalla definizione del seno:
sin β = b/c .... (1)
Ed ecco il primo semplicissimo colpo di genio: ribaltare il triangolo secondo il cateto maggiore e aggiungerlo al primo, come mostra la Fig. 2.
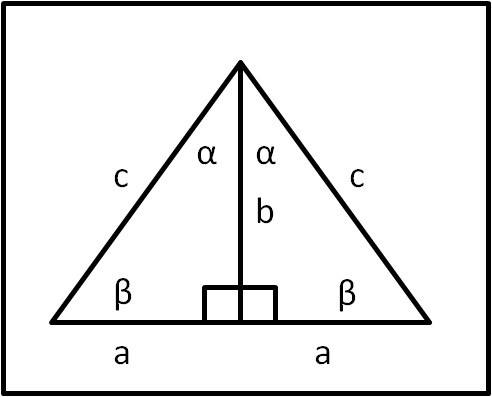
Si ottiene un triangolo isoscele a cui si può applicare il teorema dei seni. In particolare:
sin (2α)/2a = sin β/c .... (2)
Possiamo tranquillamente inserire la (1) nella (2) e ottenere:
sin (2α)/2a = b/c2
Invertiamo numeratore con denominatore
2a/sin (2α) = c2/b
e moltiplichiamo entrambi i membri per b
2ab/sin (2α) = c2 .... (3)
Abbiamo ottenuta la relazione voluta, in cui al secondo membro compare c2. Notiamo, ancora, che la relazione non ha fatto uso dell'identità trigonometrica. Cosa dobbiamo cercare di ottenere, a questo punto? Beh, è molto semplice ...
a2 + b2 = 2ab/sin (2α) .... (4)
Se valesse la (4), a causa della (3), potremmo concludere che:
a2 + b2 = c2 .... (5)
Che altro non è che il teorema di Pitagora!
Bene, complichiamo ingegnosamente la Fig. 2, aggiungendo dei triangoli simili a quello di partenza, come mostra la Fig. 3.
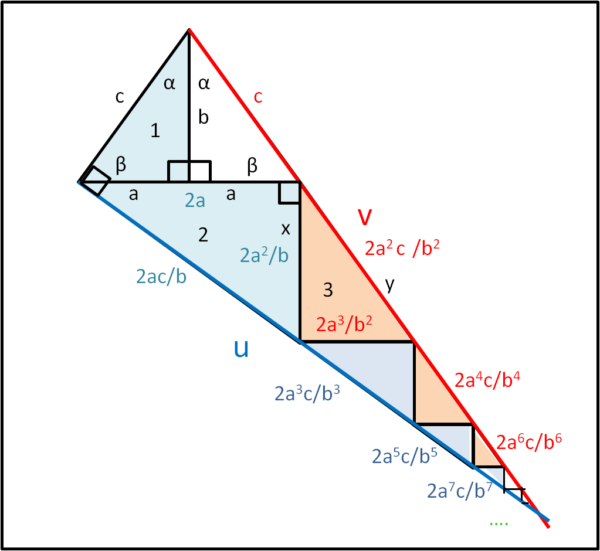
E' immediato riconoscere che tutti i triangoli che compaiono sono simili tra loro. In particolare, consideriamo i triangoli azzurri 1 e 2.
Il cateto lungo di 2 (2a) è il doppio del cateto corto di 1(a), ciò permette, data la similarità, di determinare il valore del cateto corto (x) di 2 e la sua ipotenusa.
x/2a = a/b
x = 2a2/b
Il che implica che il rapporto di proporzionalità sia (2a2/b)/a = 2a/b. Ciò comporta che l'ipotenusa di 2 sia data dall'ipotenusa di 1 moltiplicata per 2a/b, ossia 2ac/b.
Risolto completamente il triangolo 2, possiamo proseguire con il triangolo 3. Determiniamone, ad esempio, l'ipotenusa y:
yb/2ac = 2a2/2ab
y = 2a2c/b2
Il rapporto di proporzionalità tra 2 e 3 è diventato (2a2c/b2)/(2ac/b) = a/b.
A questo punto, gli infiniti triangoli sia azzurri che rosa che seguono mantengono per costruzione lo stesso rapporto di proporzionalità tra di loro. Ciò vuol dire che per avere la successiva ipotenusa del triangolo azzurro, basta moltiplicare quella di 2 per il rapporto a/b e via dicendo... così come viene indicato nella Fig. 3.
In poche parole, il lato u è dato dalla somma dei termini che contengono le potenze dispari di a/b:
u = 2ac/b + 2a3c/b3 + 2a5c/b5 + 2a7c/b7 + ..... .... (6)
Le ipotenuse dei triangoli rosa contengono le potenze pari di a/b.
v = c + 2a2c/b2+ 2a4c/b4+ 2a6c/b6 + ..... .... (7)
Prima di proseguire diamo un'occhiata al triangolo che contiene tutti i triangoli aggiuntivi. Anch'esso è rettangolo e ha u come cateto lungo e v come ipotenusa. Ne segue che:
u = v sin(2α) .... (8)
Una semplice relazione trigonometrica immune dall'intoccabile identità.
Non ci resta che analizzare, in dettaglio, e manipolare un pochino, le due sommatorie che forniscono u e v. Cominciamo con u
u = 2ac/b + 2a3c/b3 + 2a5c/b5 + 2a7c/b7 + .....
u = (2ca/b)((a2/b2) + 2c(a4/b4) + 2c(a6/b6) + .....
u = (2ca/b) ∑1∞(a2/b2)n - 1
ponendo k = n - 1
u = (2ca/b) ∑0∞(a2/b2)k
Ricordiamoci la serie geometrica
∑0∞qk
se q < 1
la serie converge e ha per somma:
∑0∞qk = 1/(1 - q)
Nel nostro caso a2/b2 < 1
Per cui possiamo scrivere:
u = (2ca/b) (1/(1 - a2/b2))
u = 2abc/(b2 - a2) .... (9)
Passiamo a v:
v = c + 2a2c/b2+ 2a4c/b4+ 2a6c/b6 + .....
v = c + 2a2c/b2 ∑1∞(a2/b2)n - 1
ponendo k = n - 1
v = c + 2a2c/b2 ∑0∞(a2/b2)k
Siamo nuovamente di fronte a una serie geometrica, per cui possiamo scrivere:
v = c + (2a2c/b2 )(1/(1 - a2/b2))
v = c + 2a2c/(b2 - a2)
v = (c(b2 - a2) + 2a2c)/(b2 - a2)
v = (cb2 + ca2 )/(b2 - a2)
v = c(b2 + a2)/(b2 - a2) .... (10)
La nostra attenzione è subito attratta dalla presenza (sperata e cercata) di a2 + b2
Non ci resta, adesso, che richiamare la (8) e inserire al suo interno i valori ottenuti di u e di v.
sin(2α) = u/v
sin(2α) = (2abc/(b2 - a2))/(c(b2 + a2)/(b2 - a2))
sin(2α) = 2ab/(b2 + a2)
2ab/sin(2α) = a2 + b2 .... (11)
A questo punto, richiamiamo la (3)
2ab/sin (2α) = c2
Il primo membro è esattamente uguale al primo membro della (11), per cui devono essere uguali anche i secondi membri, ossia:
a2 + b2 = c2
c.v.d.
Permettetemi di fare una mia personalissima riflessione...
Il mondo odierno è un mondo soprattutto "occidentale", ossia è ancora nelle mani dell'Europa e dell'America del Nord. La storia ha permesso, per vari motivi, agli europei e agli americani di essere i "padroni" del mondo, con conseguenti stragi, distruzione di civiltà, guerre sanguinose, ecc. Lo sfruttamento dei più deboli ha portato al razzismo più bieco, ancora oggi imperante. Il teorema era ed è ancora parzialmente lo stesso: chi sa usare meno le armi ha sicuramente il cervello inferiore. E così milioni di bambini in Africa e in Asia (ma non solo) sono usati come schiavi dall'Occidente e dalle sue ipotetiche conquiste tecnologiche. Basta pensare alle miniere del Congo, alle guerre tra tribù e ai bambini soldato. Quando manca il cibo è difficile aver tempo di pensare... Tutto questo è profondamente ingiusto.
Mi fermo, spesso, a pensare a quanti bambini talentuosi, con colore della pelle diversa dalla nostra, avrebbero potuto e potrebbero dare un contributo fondamentale -e decisamente migliore- all'evoluzione della specie umana. Una specie che, comunque, è appena nata e ha già visto cambiamenti drastici. Non dimentichiamo che l'homo sapiens è di origine africana ed è riuscito a prevalere su tutte le altre specie durante i durissimi secoli dell'era glaciale.
Altre civiltà sono state soggette ad alti e bassi e, oggi, volenti o nolenti, ci troviamo di fronte a nazioni, come l'India e la Cina, che vogliono riprendere il predominio sia sociale che intellettuale. Chi vivrà vedrà... per il momento fatemi essere estremamente felice che questa opera d'arte matematica sia stata realizzata da due giovani col colore nero della pelle, ma dal cervello più "bianco" di tanti altri dalla pelle più chiara. Cervelli che si stanno autodistruggendo seguendo solo la tecnologia della "pappa pronta", dell'arroganza e dell'interesse del singolo.
P.S.: i 5 asterischi si riferiscono all'idea, mentre i 3 si riferiscono ai calcoli da eseguire.






5 commenti
Bella dimostrazione!
Quanto alla tua personalissima riflessione non può che essere condivisa. L'arroganza, a braccetto con l'ignoranza, non possono che generare catastrofi.
Vincenzo non posso che condividere la tua riflessione riportata a fondo articolo.
Curioso dell'argomento sono andato sul Web e mi pare di aver letto che la dimostrazione trigonometrica fatta dalle due geniali ragazze liceali non sarebbe ancora sta avvallata sala comunità scientifica internazionale.
Ma dall'articolo da te scritto è molto evidente la rigorosa logica riportata nella dimostrazione
Caro Michele,
direi che rimane la parte "burocratica"... La dimostrazione è bellissima e poco importa che sia completamente o parzialmente trigonometrica. L'idea delle due serie è a dir poco "sublime"...
Geniali le due studentesse liceali che pur usando la trigonometria non si sono servite della relazione fondamentale della stessa che pone in relazione i quadrati delle due funzioni (sin e cos) analoga al teorema di Pitagora.
Poi il ricorso alla serie geometrica e dir poco un pensiero sublime per due giovincelle
Vincenzo per la dimostrazione si è utilizzato il criterio di convergenza delle serie geometriche che risulta convergere alla quantità finita 1/1_q in cui q nel caso in esame è dato da a2/b2 .
Questo si verifica perché il triangolo preso in esame ha a<b ovvero il triangolo rettangolo è scaleno ma se il triangolo rettangolo fosse isoscele con a=b la ragione q della serie sarebbe q=1 e la serie non sarebbe convergente ma divergente.
In questo caso la dimostrazione non sarebbe applicabile?