Questo articolo è inserito in Meccanica Classica

 

Mentre stiamo affrontando la cinematica più semplice attraverso esercizi che ne permettano una comprensione sempre più accurata, descriviamo qualche altra grandezza della fisica classica che ci verrà sicuramente utile in seguito.

Mi sono accorto che non ho dato abbastanza visibilità al momento d'inerzia o, quantomeno, poco è stato fatto per descrivere come si ottengono i valori delle forme più comuni.

Poche parole per ricordare cos'è il momento d'inerzia. Da un certo punto di vista esso è molto simile alla massa di un corpo. Nei moti traslatori, abbiamo a che fare con la massa, ossia con l'inerzia di un corpo a cambiare il suo stato di moto uniforme. D'altra parte, sappiamo bene che se applichiamo una certa forza a un oggetto esso è costretto a cambiare la propria velocità costante e subire un'accelerazione. Ebbene se la stessa forza è applicata a un corpo di massa maggiore, la risposta  sarà inferiore, ossia l'accelerazione sarà decisamente più piccola. La massa, quindi, è un qualcosa che si oppone alle forze che tentano di disturbarne il moto a velocità costante (o in quiete se la velocità è zero).

Se un oggetto viene posto in rotazione attorno a un certo asse, esso si "ribella "al moto che gli si sta imponendo, attraverso il momento d'inerzia.

Iniziamo col considerare un punto di massa m. Il suo momento d'inerzia dipende ovviamente dalla massa del corpo, analogamente all'inerzia traslatoria, ma anche dalla distanza dal punto di rotazione. In particolare, maggiore è la distanza da quest'ultimo e maggiore è il momento d'inerzia. In parole matematiche, il momento d'inerzia I di un punto di massa m vale:

I = mr²                                 .... (1)

dove m è la la massa e r la distanza del punto dall'asse di rotazione. Come si vede la distanza è al quadrato e quindi essa ha un ruolo molto più importante della massa nel cercare di ostacolare la rotazione. Questo fatto ci porta a capire facilmente che mentre la massa è una proprietà intrinseca di un corpo (quella è in qualsiasi sistema di riferimento), il momento d'inerzia, invece, dipende dalla distanza che è grandezza del tutto estranea al corpo in rotazione. Se cambio la distanza cambio l'inerzia rotatoria, a parità di massa.

Ne segue che non ha senso parlare di momento d'inerzia di un oggetto senza specificare l'asse di rotazione.

La formula (1) riguarda, però, solo corpi puntiformi dotati di massa. Se consideriamo forme macroscopiche più strane è necessario saper valutare bene la risposta alla rotazione delle varie parti dell'oggetto, dato che alcune sono più vicine, altre più lontane dall'asse di rotazione. Ne segue che ogni forma, per semplice che sia, ha il suo proprio momento d'inerzia, che, come già detto, può variare in base all'asse di rotazione.

Cosa succede se consideriamo un insieme di punti che ruotano tutti assieme attorno a un certo asse? Se essi mantengono le loro posizioni reciproche è facile concludere che il momento d'inerzia dell'insieme di punti non è altro che la somma dei momenti d'inerzia di ogni singolo punto.  Questo fatto ci porta velocemente verso il momento di un corpo rigido di forma qualsiasi. Se il corpo è rigido vuol dire che ogni suo punto si muove solidalmente con gli altri e, quindi, il momento d'inerzia del corpo non è altro che la somma dei momenti d'inerzia di ogni singolo punto del solido. A parole è semplice, ma per poter agire è necessario saper esprimere l'insieme di tutti i punti del corpo. In poche parole deve intervenire il volume (o la superficie p la lunghezza) del corpo, tenendo conto che la distanza dall'asse di rotazione è diversa per ogni singolo punto.

Scriviamo il momento d'inerzia come sommatoria di momenti

I = Σ m_i r_i²

la "i" varia da 1 a n, ma per un n finito non avremo mai una rappresentazione esatta del corpo. Cosa possiamo fare? Far tendere a zero la massa di ogni singolo punto in modo che si abbia a che fare con infiniti punti. In altre parole calcolare il limite della (2) per m che tende a zero.

Agendo in tal modo passiamo dal calcolo di una sommatoria al calcolo di un integrale, che deve essere esteso a tutto il volume del corpo (se è tridimensionale). Ossia:

I = ∫_V r² dm                                     .... (2)

ovviamente r deve essere scritto in modo che rappresenti la forma del corpo. Non per niente l'integrale è esteso a tutto il volume.

Facciamo subito un esempio molto semplice di applicazione della (2)

Consideriamo una barretta di ferro, omogenea, a base quadrata S e di  lunghezza d e facciamola ruotare attorno ad un asse perpendicolare alla barretta, passante per il suo punto di mezzo (Fig. 1).

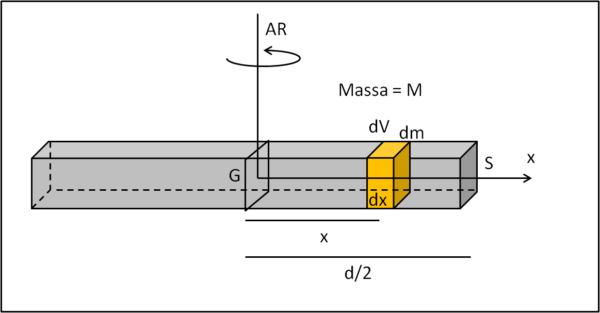
La massa totale è M. Inseriamo la barretta in un sistema di riferimento che abbia G (centro di massa) come origine. Consideriamo un volumetto dV (arancione in figura) di massa dm e lunghezza dx. Tale volumetto si trova a una distanza x dall'origine. La barretta è omogenea, per cui la sua densità ρ è uguale alla massa del volumetto diviso il suo volume, ossia:

ρ = dm/dV

dm = ρ dV

Non è difficile calcolare il volume dV, essendo il nostro volumetto un parallelepipedo:

dV = S dx

e, quindi:

dm = ρ S dx

A questo punto possiamo scrivere l'integrale (2):

I = ∫ r² dm  = ∫ x² ρ S dx

x è infatti proprio la distanza r dall'asse di rotazione e (ρ S dx ) la massa dm del volumetto. Non ci resta che stabilire l'intervallo di integrazione che deve permetterci di coprire l'intero volume della barretta. Niente di più facile, dato che basta integrare tra x₁ = - d/2 e x₂ = d/2. Notiamo che un integrale esteso ad un volume si può trattare in questo caso come un integrale esteso solo ad una lunghezza, moltiplicata per delle costanti:

I =∫_-d/2 ^d/2(x² ρ S) dx

L'integrale è semplicissimo dato che vale x³/3 (la sua derivata è proprio  3x²/3 = x²) , per cui:

I =ρ S [x³/3 ]_-d/2^d/2 = (ρ S/3) (d³/2³ + d³/2³ ) = (ρ S/3) 2 d³/8 = (ρ S/3)d³/4

I = ρ S d³/12             .... (3)

Noi, però, vogliamo che il momento d'inerzia abbia la forma "classica" ossia sia dato dalla massa moltiplicata per il quadrato di una distanza. Nessun problema...

ρ =M/V = M/(S d)

e la (3) diventa:

I = (M/(S d)) (S d³/12)

I = 1/12 Md²

Possiamo concludere che il momento d'inerzia è uguale alla massa totale moltiplicata per la lunghezza della sbarra (ossia, massa moltiplicata per il quadrato di una lunghezza). Il tutto va, però, moltiplicato per il coefficiente 1/12, che dipende dalla configurazione considerata, ossia la rotazione della barretta attorno all'asse perpendicolare passante per il suo centro di massa.

Notiamo bene una cosa: il momento d'inerzia si utilizza nei moti rotatori, ma esso non ha niente a che vedere con la rotazione, in quanto è una grandezza che dipende solo dalla forma dell'oggetto e dall'asse di rotazione. Come la massa, esso esiste per un certo corpo, indipendentemente dal fatto che esso trasli o ruoti o stia fermo.

A questo punto abbiamo le nozioni sufficienti per calcolare i momenti d'inerzia delle figure più comuni. Normalmente, viene dato un elenco dei momenti d'inerzia e si trascura la loro determinazione. Noi, invece, descriveremo il metodo che ci permetterà di determinare il momento d'inerzia, partendo solo dalla definizione data dalla (1). Come sempre, un certo problema si può risolvere in vari modi. Noi sceglieremo quelli che utilizzano alcuni semplici integrali in modo da prendere sempre maggiore dimestichezza con questa operazione che può diventare un ostacolo praticamente insormontabile per certe funzioni.

Abbiamo già ricavato il momento d'inerzia di una barretta attorno a un asse ad essa perpendicolare, passante per il baricentro. Nei prossimi articoli, indicati con (MI) nel titolo, penseremo a un anello e a un disco sottili per poi passare al cilindro e alla sfera.