Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Giorno per giorno…

Le figure utilizzate fino ad ora sono estremamente utili, dato che permettono di calcolare immediatamente la declinazione del Sole rispetto all’equatore di Giove e, confrontandola con il valore limite di visibilità dei vari transiti satellitari, sapere se il nostro Super Kepler naturale stia compiendo osservazioni fruttuose. In qualche modo, però, siamo più che rilassati, dato che qualsiasi siano le condizioni momentanee, sappiamo benissimo che prima o poi il Sole arriverà ai nodi N e N’ e potrà vedere l’equatore di Giove “di taglio”. Sto parlando, ovviamente, delle figure come la Fig. 11, dove i punti sicuramente utili sono proprio N e N’.

Cosa ci dice questa ovvia constatazione? Un fatto importantissimo che spesso porta a grandi confusioni in chi cerca di spiegare senza avere capito veramente la problematica. L’inclinazione dell’orbita di Giove rispetto all’equatore gioviano ha un’importanza abbastanza relativa. Nel senso che se fosse troppo alta si potrebbero osservare i transiti solo avvicinandosi ai nodi N e N’. Vi ricordate cosa abbiamo detto nel primo capitolo? Potrebbe anche essere inclinata di 90°, ma due punti fortunati per vedere i transiti l’avremmo sempre e comunque.

Il fatto che l’orbita sia inclinata di soli 3° è, però, sicuramente un vantaggio in più, perché permette di vedere i transiti dal Sole lungo quasi tutta la sua orbita. Notate, inoltre, che dell’inclinazione dell’orbita gioviana rispetto all’orbita terrestre non abbiamo assolutamente parlato. E ne parleremo ben poco, dato che la sua importanza è ancora più relativa, malgrado si legga in giro che è proprio questa inclinazione molto piccola  a permettere i fenomeni mutui. Assolutamente no, come vedremo…

Torniamo al nostro SK solare. Le rappresentazioni usate nelle figure precedenti ci ricordano qualcosa che usiamo spesso e volentieri per la nostra Terra. Infatti, quando disegniamo sulla sfera celeste l’equatore terrestre e l’eclittica identifichiamo, immediatamente, le stagioni. Il nodo ascendente è il punto d’Ariete (γ), dove comincia la primavera e quello opposto il punto della Bilancia (Ω) dove inizia l’autunno. Nei due punti a 90° si hanno i solstizi. Insomma, quella figura ci indica chiaramente che nei nodi il Sole passa da declinazioni negative a positive e viceversa. Nei nodi, ovviamente, l’equatore è visto di taglio dal Sole e la durata del giorno e della notte sono uguali dappertutto. Cose ben note e quasi ridicole. Tuttavia, fatemi disegnare la situazione “terrestre” nella Fig. 14.

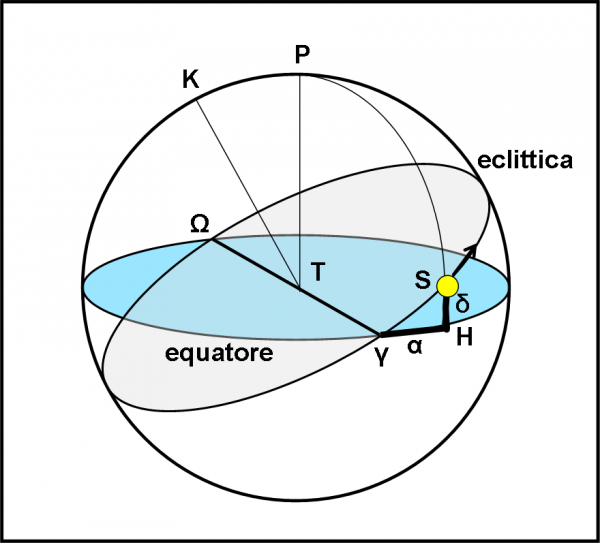
Essa può facilmente essere trasformata in un diagramma ancora più leggibile e facilmente utilizzabile. Il Sole compie un giro completo sulla sfera celeste (da nodo ascendente a nodo ascendente, ad esempio) esattamente in un anno, ossia in 365 giorni circa. Possiamo anche dire che, in prima approssimazione, il Sole percorre la sua traiettoria sulla sfera celeste a velocità costante (orbita circolare). Esiste quindi un legame semplice e diretto tra ascensione retta e tempo. La prima compie i suoi 360° (o se preferite 24 ore), il secondo l’anno.  Diventa quindi banale trasformare la nostra sfera celeste e tutti i suoi archi ed archetti che comporterebbero la conoscenza della trigonometria sferica, in un diagramma disegnato su un piano, attraverso delle coordinate cartesiani, nostre care amiche.

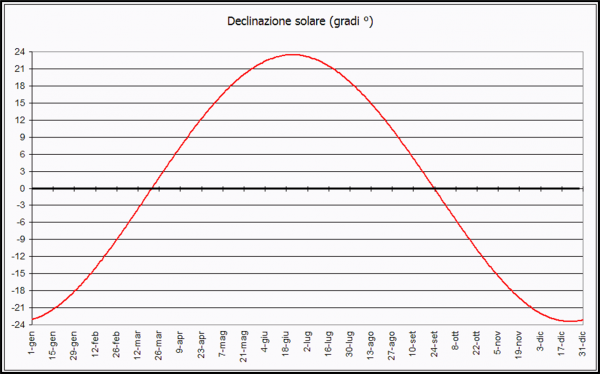
L’ascensione retta si può trasformare tranquillamente in tempo, misurato in mesi, giorni, ore, ecc., la declinazione resta quella che è. In ascissa mettiamo il tempo e in ordinata la declinazione geocentrica del Sole. Otteniamo la Fig. 15, di immediata comprensione. Una bellissima sinusoide (vedi funzioni trigonometriche nella sezione matematica…). Dove essa taglia l’asse delle ascisse si trovano i nodi, ossia gli equinozi (declinazione uguale a zero); dove raggiunge il massimo e il minimo vi sono i solstizi. Una figura comodissima che permette di trovare graficamente la posizione del Sole, rispetto all’equatore, in ogni momento dell’anno. Notate che il massimo (e il minimo) valgono proprio i famosi 23° dell’inclinazione dell’orbita terrestre. Cosa che le figure dei primi capitoli dovevano già farci intuire da molto tempo.

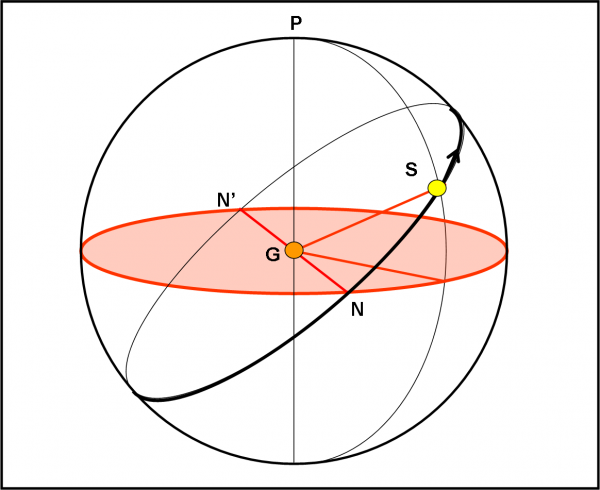
Perché non usare la stessa figura anche per Giove? Le figure usate finora sono proprio dello stesso tipo, come dimostra lo schema di massima mostrato in Fig. 16 (è un’ennesima ripetizione, ma meglio averla sempre vicina). Bisogna solo ricordare che il Sole gira intorno a Giove (o il viceversa) non in un anno terrestre ma in un periodo un po’ più lungo, ossia in quasi dodici anni terrestri (11.86). Problema insignificante, dato che possiamo continuare a utilizzare i giorni e i mesi terrestri. La sinusoide di Giove si chiuderà solo dopo un periodo più lungo, ma tutto il resto rimane analogo.

Tracciamo in Fig. 17 la Fig. 15 terrestre, riferita questa volta a Giove. Il tempo è ovviamente espresso in giorni terrestri (per comodità). Si notano i due nodi (dove il piano equatoriale viene visto di taglio) e il massimo e il minimo che raggiungono a malapena i 3.1° di declinazione giovi centrica (proprio l’angolo tra orbita gioviana e il suo equatore). Questa figura non fa altro che rappresentare le stagioni di Giove! Tuttavia, a noi non importano le stagioni, ma i transiti dei satelliti.

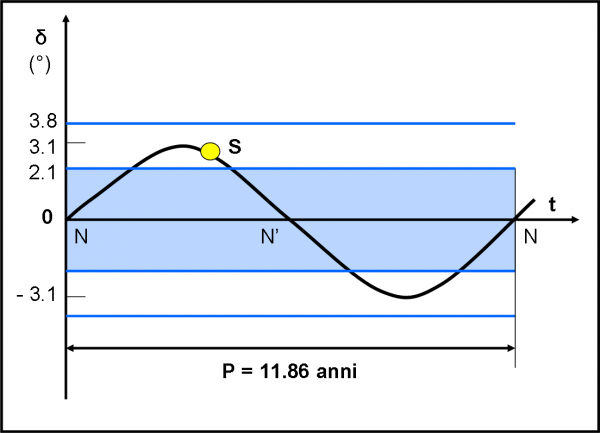
E’ immediato, allora, disegnare nella stessa figura anche quei famosi “paralleli” azzurri usati nel capitolo precedente. Ricordiamo che essi sono il luogo dei punti che hanno, come declinazione, quella limite relativa a ogni satellite. Beh… se hanno sempre la stessa declinazione, quei paralleli diventano delle rette parallele all’asse x (ossia all’asse del tempo) nella Fig. 17. Disegniamole, ovviamente, come linee azzurre. Ne ho disegnato solo due. Perché? Ma è ovvio: i primi tre satelliti si vedono dal Sole sempre con angoli minori di quello limite (ho inserito solo quello di Ganimede, pari a 3.8 gradi, trascurando Io ed Europa che sono nettamente più in alto). La sinusoide è sempre più bassa di queste tre linee. La linea di Callisto, invece, si trova un po’ più bassa e la Fig. 17 ci mostra molto bene quando il Sole la taglia. In poche parole, se il Sole si trova all’interno della banda azzurra TUTTI i transiti sono sempre visibili. Una figura veramente comoda e facilissima da usare. E, soprattutto, costruibile con foglio e matita.

Non ce ne sarebbe bisogno, ma fatemi fare una “sciocca” precisazione. Stiamo sempre parlando di Sole che osserva i transiti. La situazione è, però, identica a quella di Giove che vede il Sole occultato dai suoi satelliti. Posso permettermi di stare su Giove e pensare a quello che vede il Sole proprio per questa possibilità di scambio dei ruoli. Capita lo stesso anche per una stella, un suo pianeta e Kepler. Se Kepler vede un transito di un pianeta davanti alla stella, esiste sicuramente una zona della stella da cui si “vedrebbe” il pianeta passare davanti a Kepler…

Sul Sole fa troppo caldo, ma possiamo accendere la luce!

E’ comunque giunta l’ora di abbandonare il nostro telescopio naturale. Ci siamo accorti che fa troppo caldo e che le osservazioni eseguite dal Sole sono veramente difficili (specialmente d’estate… ah ah ah…). E’ un vero peccato, perché è su una traiettoria ideale per assistere ai transiti…

Un attimo, un attimo… il Sole non è solo un osservatore “passivo”, ma è un  osservatore  “attivo”. Super Kepler deve sperare nella luce della stella che viene bloccata dal suo pianeta, ma il Sole è capace di inviare luce e molta di più di quella che è capace di emettere Giove (che poi non fa altro che sfruttare quella del Sole attraverso la riflessione…). Accidenti, è vero! Se Maometto non va alla montagna, la montagna può andare da Maometto. Invece di usare il Sole come osservatore e basta, utilizziamolo proprio come stella (speriamo che non si sia offeso…).

Tutta la trattazione che abbiamo fatto finora, però, non cambia di una virgola. Dobbiamo solo cambiare il modo di “dire” le cose. Un transito di un satellite davanti a Giove visto dal Sole, diventa un’eclisse di Sole su Giove da parte del satellite. La luce viaggia, in prima approssimazione, in modo rettilineo e quindi ciò che vede il Sole può essere considerato ciò che il Sole invia verso Giove. La Fig. 18 illustra, banalmente, la nuova situazione.

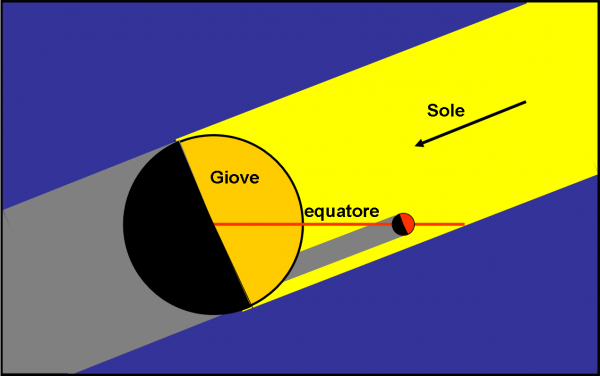
L’importante è che la Fig. 17 (e quelle precedenti) restino invariate e continuino a essere valide per i nostri scopi. Invece di dirci quando e come il Sole vede i transiti, ci dicono, adesso, quando e come l’ombra dei satelliti, dovuta alla luce solare, si proietta sul pianeta. Insomma, ci dicono quando capitano le eclissi di Sole causate dai satelliti medicei.

Qualcuno mi dirà: “Va bene, abbiamo evitato il caldo del Sole… ma non è che andare su Giove sia molto meglio. A parte i costi, è difficile camminare sulla sua atmosfera…”. No, no, non c’è bisogno di andare su Giove. Mentre un transito è qualcosa che necessita la presenza fisica sulla linea in cui avviene (vedi SK), un’eclissi può essere vista anche da altre posizioni. Ciò che interessa è vedere quella macchiolina nera dovuta all’ombra del satellite… Questo è il grande vantaggio delle eclissi!

Come facciamo a sapere da dove si possono vedere le eclissi di Sole su Giove? Basta usare, nuovamente, carta e matita e fare un disegno a dir poco elementare. Utilizziamo la Fig. 19.

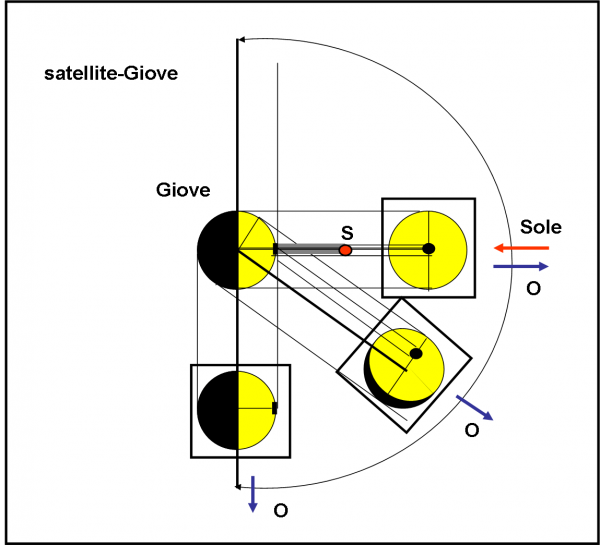
Immaginiamo che il piano del foglio sia quello perpendicolare al piano che contiene Sole, satellite e Giove. Possiamo anche considerare, più semplicemente, che esso sia proprio il piano equatoriale di Giove, tanto la situazione finale non cambia. La luce del Sole proviene orizzontalmente da destra (freccia rossa). Il satellite S la intercetta e causa il cilindro d’ombra (parliamo di cilindro e non di cono, dato che il Sole è abbastanza lontano da Giove rispetto alla distanza dei satelliti) che proietta la macchia nera sul disco planetario. Dove bisogna trovarsi per poter vedere questa macchiolina? In parole povere, potrei dire: “Ovunque sia visibile l’emisfero di Giove che contiene la macchiolina”.

Sicuramente non vedrei niente se andassi dalla parte opposta di Giove rispetto al Sole. In quel caso vedrei l’emisfero in ombra. E’ facile, però, notare che la macchia è ancora visibile perfino dalla posizione perpendicolare alla direzione del Sole, sia in basso che in alto. Ossia ci si può spostare tranquillamente di un angolo di 180° senza perdere lo spettacolo. In particolare, nei due casi estremi, la macchiolina sarebbe proprio sul bordo di Giove e sarebbe praticamente un punto quasi impercettibile. Tuttavia, basta spostarsi un pochino verso il centro. Per facilitare la comprensione della situazione, ho inserito, per tre direzioni particolari, ciò che l’osservatore vedrebbe dalla rispettiva posizione. Queste tre osservazioni sono inserite nei rettangoli. Esse rappresentano il pianeta visto su un piano perpendicolare alla linea di vista. L’ombra è sempre ben visibile tranne che nel punto a 90°, dove si intuisce appena. In ogni modo, direi che non c’è proprio da preoccuparsi! Quando avviene un’eclisse (e sappiamo, dalle figure precedenti, che questo è un evento quasi continuo, tranne per quel piccolo intervallo negativo di Callisto) lo spettacolo è assicurato.

Attenzione: quello che ho disegnato sul piano del foglio vale anche per osservatori posti su un piano perpendicolare al foglio o su qualsiasi piano che passa per la direzione Sole-Giove, dato che la geometria è identica. In questo enorme emisfero di visibilità ci sta tranquillamente anche la Terra, ovviamente…

Non vogliamo, però, ancora tirarla in ballo e continuiamo a guardare cosa succede intorno a Giove. Torniamo anche a parlare di osservatore Solare, tanto sappiamo benissimo che il tutto può essere ribaltato considerando i transiti come delle eclissi: basta che l’osservatore Sole diventi attivo e accenda la luce!

Qualcuno potrebbe dirmi: “Ti è piaciuto vincere facile!” Avrebbe anche ragione. In fondo, Giove è enorme rispetto ai suoi satelliti, che gli sono anche molto vicini. Oltretutto, il piano orbitale di Giove è inclinato di pochissimo rispetto all’equatore del gigante. Tutte queste caratteristiche hanno permesso una visione continua dei fenomeni mutui tra satelliti e Giove, sia se li chiamiamo transiti, visti dal Sole, sia se li chiamiamo eclissi, visti da Giove (o da osservatori distribuiti un po’ ovunque nello spazio “teatrale”). In realtà, di mutuo c’è stato ben poco finora. Beh…sì, è colpa mia che non vi ho mai parlato della scomparsa dei satelliti dietro a Giove. Se ragioniamo sui sistemi planetari stellari, questi eventi sarebbero le eclissi secondarie, ossia quelle relative al passaggio del pianeta dietro alla stella. Scientificamente sono molto interessanti, comunque, ma sono di ben più facile trattazione e li lascio a voi. Può essere un ottimo esercizio per controllare se avete capito bene tutta la strategia grafica.

Per non far diventare questi articoli una specie di Divina Commedia (come lunghezza, ovviamente…), inseriamo, invece, una difficoltà in più, in modo che non mi possiate accusare di “vincere facile”. Andiamo ad analizzare qualcosa di molto meno frequente, ossia le occultazioni o transiti o eclissi tra i satelliti di Giove. Il pianeta non interessa più, ma interessano solo i suoi quattro figlioli. Mamma mia, che problema gigantesco… Forse c’è proprio bisogno di … celestia & Co. No, assolutamente no. Potreste risolvere il tutto da soli, dato che non dovete fare altro che ripetere pari pari quanto fatto finora, cambiando solo il raggio di Giove e la distanza dei satelliti. Tutta la strategia grafica e logica restano uguali e i risultati sono di facilissima interpretazione. Magari pensateci sopra e precedetemi…

Alla prossima…