Questo articolo è stato inserito nelle sezioni d'archivio "Sistema Solare", "Astronomia classica" e "Giove e i suoi tesori"

I satelliti di Giove hanno cominciato a giocare a nascondino tra di loro. Un fenomeno ricorrente che assume ancora un’importanza professionale. Vale la pena cercare di capire bene la configurazione geometrica che li rende possibili. Niente di difficile e completamente descrivibile con un foglio e una matita, senza bisogno di programmi prefabbricati che vengono presi a scatola chiusa. Sono sicuramente affascinanti, ma insegnano poco o niente. Continuo a lottare a favore della mente e contro la pappa pronta che vogliono imporci media e internet. Seguire questo lungo articolo è, inoltre, un fondamentale esercizio di geometria che non può che aiutare in contesti ben più generali. Spazio-tempo, multiversi, meccanica quantistica, relatività, ecc., ecc., sono argomenti affascinanti, ma senza le basi della geometria, della matematica e della fisica elementare, rimangono soprattutto belle "parole", ma sempre troppo lontane per essere veramente tangibili.

Devo dire subito che gli eventi mutui, che saranno tra breve osservabili tra i satelliti di Giove, sono solo uno spunto per cercare di far capire come, secondo me, dovrebbero essere affrontati i fenomeni del Cosmo, da quelli più vicini a noi a quelli legati alle distanza inimmaginabili dell’Universo. Ormai mi conoscete bene e sapete che reputo fondamentale capire i concetti base, lasciando ai programmi prefabbricati il loro ruolo da “schiavi”, ossia di strumenti utili per sveltire i calcoli, ma sempre e comunque un mezzo e non un fine. Si usino pure, ma prima è necessario tornare al foglio e alla matita (e al cervello) per entrare veramente nella problematica, qualsiasi sia la difficoltà dei calcoli che si prospettano. Ricordiamo, inoltre, che un programma funziona solo se funziona la mente di chi lo ha progettato attraverso foglio e matita.

Giove e i suoi satelliti sono sempre stati una ghiotta occasione per gli astronomi. Essi sono ben visibili e mostrano, attraverso i loro movimenti reciprochi, una serie di fenomeni che possono migliorare costantemente (a mano a mano che la strumentazione utilizzata si raffina) molti parametri di importanza enorme per lo studio della dinamica e non solo. Ricordiamo che grazie a loro è avvenuta la rivoluzione scientifica galileiana e si è ottenuta la prima determinazione della velocità della luce per via astronomica. Insomma, un campo di battaglia mai obsoleto, a differenza di molti altri che ormai rimangono solo uno spettacolo prevalentemente mediatico. Chi ha l’attrezzatura fa bene a seguirli, tenendo però conto del vero interesse scientifico (non solo teatrale) e cercando di capire bene tutti i meccanismi che permettono la loro  esecuzione. Insomma, goderseli con lo spirito di questo blog.

Vi sono vari modi per introdurre i fenomeni mutui tra i satelliti di Giove. In realtà, l’articolo che avevo scritto su eclissi, occultazioni e transiti sarebbe già sufficiente per capire il succo del discorso. Tuttavia, vista l’importanza ancora attuale dei quattro oggetti medicei, vale la pena andare un po’ più a fondo. Quest’articolo, quindi, utilizzerà foglio e matita per  rendere semplici e intuitive le varie situazioni geometriche che sono alla base di tutto l’argomento, mostrando come siano un caso particolare di un quadro ben più ampio e generale. Arriveremo al bordo delle equazioni che portano alla loro risoluzione. Tuttavia, nessuna paura, non le affronteremo sia per la loro complessità sia per una certa monotonia che le accompagna. A questo serve il computer che , alla fine, fornisce dati ultra esatti che chiunque può trovare nel web. L’importante è capire come si impostano e cosa possono darci in cambio. Siamo sempre noi, però, che le prepariamo e nessun risultato grafico nasce da solo. Ciò che ci mostra un programma prefabbricato (da prendere a scatola chiusa) ce lo possiamo costruire da soli, con maggiore soddisfazione e ragionamento. Se, invece vogliamo dati veramente esatti, basta dare via libera alle equazioni e al “servo” che fa i calcoli. Insomma, vogliamo sia la carne che il pesce, ma non qualcosa che non sia né uno né l’altro.

Spero che queste mie esternazioni siano comprese per quello che vogliano significare. Uno stimolo per capire sia l’Universo e i suo giochi di prestigio, ma anche per saper dare una giusta collocazione al fantastico mezzo che è il calcolatore elettronico.

Divido l’articolo più parti. Nella prima parte parto proprio da distante. Distante nel vero senso della parola. Immagino infatti di avere a disposizione un Kepler veramente sofisticato. Talmente sofisticato che è in grado di muoversi a piacere per sistemarsi nella posizione più vantaggiosa per osservare un sistema planetario attorno a una stella che non sia il Sole. Uso questo approccio perché è estremamente semplice e perché tutti hanno ormai capito perfettamente come funziona la strategia osservativa di Kepler (forse è meglio dire… come funzionava).

1. Un Super Kepler

Quali sono i vantaggi di una partenza di questo tipo? Molti, sicuramente. Innanzitutto la sorgente di luce è una e una sola: la stella attorno a cui rivolvono i pianeti. Inoltre, la direzione secondo cui la Terra vede il sistema è una e una soltanto. Insomma, la situazione è quella che è e non “potremmo” teoricamente fare altro che accettare ciò che ci offre l’Universo con tutte le sue limitazioni. Se il piano orbitale dei pianeti ha un angolo particolare siamo in grado di vedere le eclissi, altrimenti si deve usare un’altra tecnica osservativa. A questo punto, entra in scena il Super Kepler, capace di muoversi secondo regole molto semplici e precise. Nessun sistema planetario potrà più avere segreti.

Vi sembra un discorso ben lontano da Giove e dai suoi satelliti? Assolutamente no. Piano piano il Super Kepler ci dimostrerà che la comprensione delle sue fantastiche (e semplicissime) capacità può accompagnarci facilmente verso le stagioni terrestri (e non solo) e, infine, con poche complicazioni, verso i fenomeni mutui che avvengono non solo nel sistema satellitario di Giove ma in qualsiasi altro, in tutte le configurazioni possibili. Userò, sempre e soltanto, foglio e matita e tutto scorrerà liscio come l’olio. Seguitemi e non ve ne pentirete.

Sicuramente, l’inizio vi sembrerà fin troppo banale e intuitivo. Benissimo. Solo partendo da cose semplici si può arrivare lentamente a quelle che sembrerebbero a prima vista molto complicate. Spesso, i programmi a scatola chiusa ce lo fanno pensare e… chissà che cosa sta dietro alla problematica. Assolutamente no, almeno per quanto riguarda i concetti di base per la comprensione completa del fenomeno. Tutt’altra cosa è il calcolo esatto di ciò che abbiamo capito ma di cui vogliamo avere risultati matematicamente perfetti. A questo punto, ben venga lo “schiavo” che svolgerà i calcoli e ci regalerà tutte le cifre decimali che vorremo.

La Fig. 1 ci mostra come funziona il Super Kepler. Cerchiamo di seguirla  attentamente, dato che è veramente banale. Il vecchio Kepler cosa farebbe? Bene, lui sarebbe in T1 (sulla Terra o molto vicino a lei, poco importa). In quella posizione osserva la stella S che ha due figlioli che le rivolvono attorno.  Beh… siamo abbastanza fortunati. L’equatore della stella è inclinato di un angolo φ non troppo grande rispetto alla direzione di T1. Ciò comporta una visione “frontale” come quella del riquadro relativo a T1. Uno dei due pianeti è abbastanza vicino alla stella per presentare delle eclissi mutue con la stella (chiamiamole eclissi o transiti o occultazioni, quello che preferite, il concetto è lo stesso: il pianeta passa davanti alla stella e dopo mezzo periodo è occultato da lei). L’altro, purtroppo, è troppo lontano e non riesce a fare lo stesso gioco. “Pazienza”, direbbe Kepler, “almeno uno l’ho beccato!”.  Notate che ho fatto un’ipotesi “fisica”, che posso tranquillamente accettare (soprattutto pensando ai sistemi satellitari che sono lo scopo finale del nostro racconto). Ho stabilito che i pianeti rivolvono sul piano equatoriale della stella secondo orbite circolari, ossia che  il piano orbitale di tutti i pianeti sia perpendicolare all’asse di rotazione dell’astro. Non è sempre vero, ma a noi basta e avanza. Studiando la situazione che osserva Kepler, è possibile stabilire, con queste ipotesi, l’angolo φ tra l’equatore della stella e la direzione di T1.

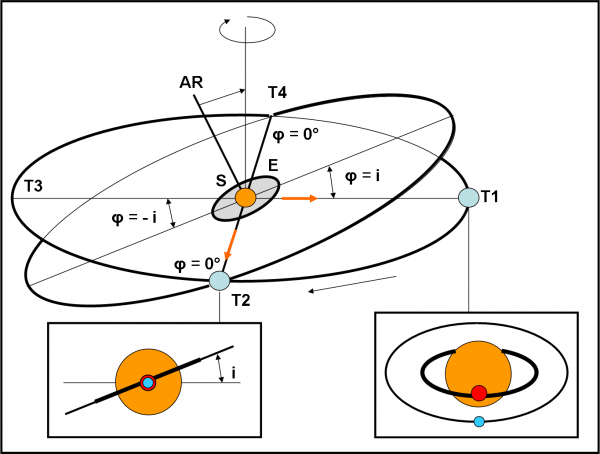
Possiamo accontentarci di questo risultato? Abbiamo avuto la fortuna di fare “trenta”, perché non fare “trentuno”. L’idea di base è: “Se esiste un pianeta, sarebbe bene cercare di trovare tutti i suoi fratelli. Magari non ci sono, ma per essere sicuri dobbiamo mettermi nelle condizioni ideali”. A questo punto entra in scena Super Kepler. Stabilito l’angolo φ, esso assume che questo non sia altro che l’angolo i tra il piano equatoriale del pianeta e un piano molto particolare che teoricamente esiste sempre (anche se non ha nessun significato fisico). Questo piano non è altro che il piano che contiene Super Kepler e la stella è e che è inclinato rispetto all’equatore dell’astro proprio dell’angolo φ. In altre parole posso determinare con facilità un piano inclinato dell’angolo i rispetto all’equatore della stella.

Ho solo cambiato nome all’angolo e costruito un piano teorico, niente di più. Tuttavia, mentre l’angolo i è un angolo fisso, tra due piani, l’angolo φ varia continuamente a seconda della direzione stella-Super Kepler. Sì, cari amici, questa è propria la caratteristica di Super Kepler. Esso è in grado di viaggiare nello Spazio, mantenendosi sempre alla stessa distanza dalla stella S. Dove avviene il suo movimento? Proprio nel piano che abbiamo appena costruito, inclinato dell’angolo i rispetto all’equatore della stella. Super Kepler descrive allora un’orbita (chiamiamola così) attorno alla stella, disposta su un piano perpendicolare alla retta verticale, che forma proprio, per costruzione, un angolo i con l’asse di rotazione della stella (perpendicolare all’equatore).

Non fatevi confondere da tante parole. Ciò che capita è comprensibile facilmente guardando la figura. Un foglio e una matita spiegano meglio di tante parole. Accendiamo i motori di Super Kepler e facciamolo girare attorno alla stella. Potremmo anche fermarci ogni tanto e vedere come cambia la configurazione geometrica stella-pianeti, ma sarebbe del tutto inutile, dato che il risultato è perfettamente prevedibile, per come è stato impostato il movimento di Super Kepler. Lo fermiamo, perciò, solo dopo 90° di rotazione. In quel punto il sistema planetario sarà in condizioni ideali. Non solo qualsiasi pianeta esistente passerà davanti (e dietro) alla stella, ma con un po’ di pazienza potremo anche vedere un pianeta passare davanti all’altro.

Perché capita questa fantastica situazione? Beh… ce la siamo costruiti noi. Siamo esattamente nel nodo tra il piano equatoriale del pianeta e il piano della pseudo-orbita di Super Kepler. In T2  l’angolo φ (angolo tra equatore e direzione ST2) diventa proprio zero e il piano equatoriale viene visto di “taglio”. Lo so, lo so, state già andando avanti col pensiero e state immaginando il moto della Terra intorno al Sole e il suo equatore inclinato di 23°. Anche lì abbiamo due piani inclinati tra di loro e la direzione Sole-Terra giace sul piano equatoriale della Terra nei suoi nodi con il piano dell’eclittica, ossia agli equinozi. Bravi, bravi…bene. Vi chiedo, però, di smettere di pensarci e tornare a Super Kepler. Arriveremo agli equinozi e alle stagioni un po’ più in là… Facciamo le cose con estrema calma… Abbiamo fatto volare una missione fantastica: vale la pena seguirla fino in fondo.

Osserviamo la stella in T2 e aspettiamo il momento in cui i due satelliti passano uno davanti all’altro (è bastata un po’ di pazienza). Magari non proprio come mostrato nel riquadro in basso, relativo alla vista frontale di T2 (troppa fortuna!), ma in qualche altra posizione lungo la loro orbita. Super Kepler ha scoperto tutto quello che c’era da scoprire e può rimettersi in moto.

Beh… non possiamo pretendere di più. Quando si arriva in T3, la situazione è identica a quella osservata in T1 (si invertono solo le eclissi tra stella e pianeta rosso), ma niente di nuovo. Quando arriviamo in T4 si ripete esattamente la configurazione ottenuta in T2. Non c’è da meravigliarsi, dato che siamo giunti nel secondo nodo delle orbite. Nessuna informazione supplementare, tranne che una constatazione: la visione migliore, quella che comporta sicuramente eclissi della stella da parte di tutti i pianeti e anche la loro reciproca occultazione, si ritrova esattamente dopo un tragitto di Super Kepler uguale alla metà del suo giro completo. In altre parole, se Super Kepler impiega un anno a girare attorno alla stella, le due configurazioni più interessanti avvengono a sei mesi di distanza una dall’altra (risultato più che ovvio, pensate ai nostri equinozi…). Se, invece, Super Kepler impiegasse 12 anni, le due condizioni ideali avverrebbero ogni 6 anni. Ricordatevelo, dato che 12 anni non è un numero scelto a caso…

Bene, la Fig. 1 non ha altro da dirci. Però, le capacità di Super Kepler vanno ben oltre. Passiamo a una caso estremamente particolare, ma molto interessante se pensiamo a Urano.

Immaginiamo che la situazione che vede Super Kepler in T1 sia quella della Fig. 2. Teoricamente, il nostro telescopio non vede assolutamente niente. Il piano equatoriale della stella è perpendicolare alla direzione T1-S e per vicini che siano i satelliti alla stella non possiamo aspettarci nessuna eclisse o transito o occultazione. Siamo nelle condizioni più sfavorevoli possibili. Tuttavia, noi non abbandoniamo la speranza e, non vedendo niente, facciamo l’ipotesi (che poi si rivelerà giusta) che la situazione sia proprio quelle della figura. Facciamo, perciò, partire Super Kepler lungo un orbita che giace su un piano perfettamente perpendicolare all’equatore della stella, supposto proprio perpendicolare alla direzione S-T1. Un gioco d’azzardo? Sì, ma non poi tanto… pensateci un po’ sopra e poi ne riparliamo.

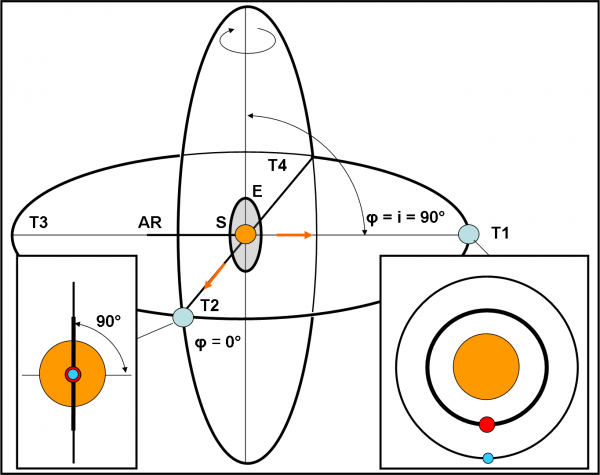
Super Kepler gira attorno al solito asse perpendicolare al piano costruito a tavolino. Che fortuna! Dopo 90° di rotazione le cose cambiano e come. La nostra ipotesi era giustissima. Il piano equatoriale della stella era proprio perpendicolare alla direzione S-T1. In T2, infatti, siamo nella linea dei nodi e si scoprono entrambi i pianeti che eclissano la stella e mostrano anche le loro reciproche occultazioni. Non c’è da dire molto di più, tranne che riflettere un attimo sul colpo di fortuna.

In realtà, il piano equatoriale poteva essere inclinato di un angolo piuttosto grande, ma non esattamente uguale a 90°. Tuttavia, anche facendo girare Super Kepler attorno a un asse non proprio “giusto”, avremmo trovato una posizione in cui il piano equatoriale sarebbe stato visto meno inclinato, permettendo di scoprire almeno un satellite e quindi anche il vero piano orbitale. A quel punto ci saremmo trovati di nuovo nelle condizioni della Fig. 1 e avremmo solo dovuto far cambiare orbita a Super Kepler. Insomma, solo un ritardo, ma la missione avrebbe comunque ottenuto lo scopo.

Torniamo alla Fig. 2. Il confronto con quella precedente ci dice che, per qualsiasi inclinazione dell’equatore della stella rispetto alla direzione stella-Super Kepler, è sempre possibile trovare una direzione in cui l’equatore si vede di taglio. Una soluzione ovvia, se ragioniamo in termini di piani inclinati di un angolo qualsiasi. Essi hanno sempre e comunque una linea dei nodi, ossia due punti in cui l’equatore viene visto di taglio.

Vi faccio notare un altro punto molto importante: finora abbiamo parlato solo di piano equatoriale della stella e direzione stella- Super Kepler o –se preferite- di una Terra che possa girare attorno alla stella. L’unico angolo importante è quello formato dall’equatore! Vedremo come sarà importante questo fatto quando arriveremo a Giove & Co.

Per completare una trattazione che è ormai diventata veramente banale e intuitiva, disegniamo anche la Fig. 3. Beh… qui siamo nel caso più fortunato possibile. Super Kepler non ha nessun bisogno di sprecare carburante. La stella ha il piano equatoriale proprio diretto verso di lui, ossia l’angolo tra equatore e direzione di vista è proprio zero. Senza nemmeno muoversi vediamo già il sistema planetario di taglio. Se costruissimo un’ipotetica orbita come quelle delle figure precedenti faremmo girare Super Kepler proprio nel piano equatoriale della stella. Qualsiasi direzione stella Super Kepler si comporterebbe come linea dei nodi. E’ ovvio: il piano orbitale e l’equatore coincidono!

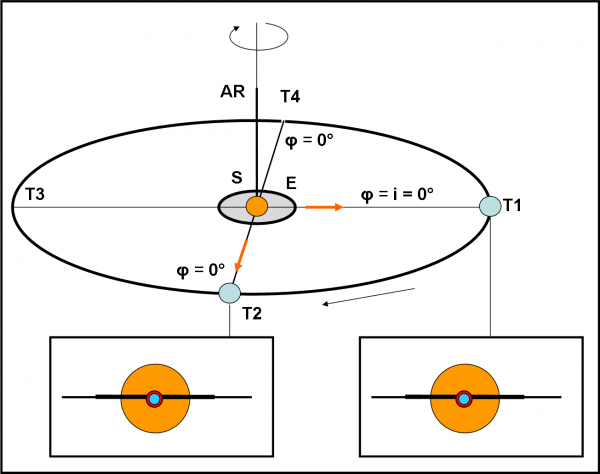
Prima di concludere questa prima parte, vi invito a riflettere su una constatazione molto importante (che interessa soprattutto lo studio delle curve di luce degli asteroidi: vedete quante applicazioni esistono se prendiamo un caso veramente generale?): per qualsiasi inclinazione tra due piani è sempre possibile trovare una direzione che mostri il piano equatoriale visto di taglio (la linea dei nodi). E’ invece unico il caso in cui si riesce a vedere il piano equatoriale “di fronte”, ossia perpendicolare alla direzione oggetto-osservatore. Ciò capita solo se l’asse di rotazione giace nel piano della pseudo-orbita. E questo fatto ci fa di nuovo pensare a Urano…

Vi invito a leggere e rileggere questa prima parte: se capite bene questa trattazione semplificata, non vi saranno più problemi per comprendere la più complessa geometria del sistema di Giove (o di Saturno o del pianeta che volete). Basterà cambiare la pseudo orbita di Super Kepler con un movimento che la Terra compie realmente. Impareremo, tra l’altro, che l’inclinazione dell’orbita di Giove riveste un’importanza del tutto trascurabile, contrariamente a quanto, a volte, si legge sul web.

2. Sistemi di riferimento

Prima di continuare nel nostro lento avvicinamento a Giove e ai suoi figlioli, fatemi ricapitolare quanto abbiamo appena imparato da Super Kepler.

1)      Indipendentemente dall’inclinazione esistente tra piano equatoriale del sistema stellare e linea di vista, se potessimo girare intorno a lei come fa Super Kepler, troveremmo almeno una configurazione che ci permette di assistere al transito dei pianeti davanti alla stella.

2)      Questa configurazione è però fin troppo fortunata, in quanto non solo permette di assistere al transito dei pianeti davanti alla stella, ma ci fa vedere il piano equatoriale proprio di taglio.

Imparate queste nozioni banalissime, lasciamo per un attimo da parte il nostro Super Kepler (SK) e torniamo al più concreto Kepler o, addirittura, alla Terra.

In altre parole, accontentiamoci, per adesso, del passaggio dei pianeti davanti alla stella nelle condizioni che la fortuna ci ha regalato, ossia la posizione relativa dell’ equatore della stella rispetto alla linea di vista. Come ben sappiamo, le condizioni di visibilità di un sistema planetario dipendono dall’ inclinazione sotto la quale vediamo l’equatore della stella, sempre sotto l’ipotesi che i pianeti rivolvano in quel piano.

Sì, giustissimo, ma ciò che veramente comanda tutto il gioco sono il diametro della stella e la sua distanza dai pianeti. Indipendentemente da dove si trovi l’osservatore (Kepler), cosa determina chi e come vede i transiti o eclissi, o quello che volete, dipende primariamente dalla geometria intrinseca del sistema stellare.

Avviciniamoci quindi alla stella e scopriamo le condizioni di osservabilità che essa e i suoi pianeti impongono a chiunque voglia assistere alla loro danza. Una semplicissima analisi grafica ci permette di scrivere le condizioni limite. Un gioco veramente da ragazzi che probabilmente avevo già trattato in articoli precedenti, ma che vale la pena riproporre per non obbligarvi a saltare di qua e di là. Disegniamo, allora, la Fig. 4. Niente si speciale… Al centro la stella A che ha un certo raggio r. Orizzontalmente ho tracciato il suo equatore (immaginiamo di vedere il tutto in un piano perpendicolare all’equatore, quello che ci permette di ottenere i parametri più importanti, come vedremo tra poco).

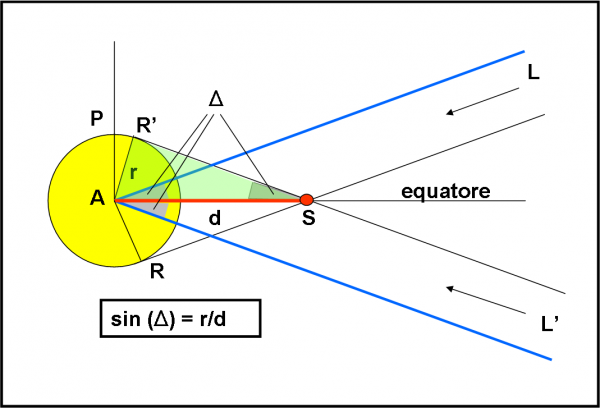
Basta conoscere il raggio della stella? Assolutamente no. E’ anche necessario sapere la distanza dei pianeti dalla stella. Per poter assistere ai transiti di ogni figliolo, consideriamo ovviamente quello più esterno (più lontano dalla stella), dato che è sicuramente lui quello che limita di più le condizioni di visibilità.  Chiamiamo questa distanza d. Abbiamo, adesso, tutti i parametri per scoprire chi e come può vedere i transiti planetari. Ci interessa ovviamente la soluzione limite, ossia quella che permette di vedere l’ultimo satellite sfiorare il bordo della stella. Un leggero spostamento (vedremo da che parte) annulla i nostri sforzi.

Non è difficile tracciare la direzione dell’osservatore L’ che vede questa condizione limite. Basta disegnare la linea che passa per il pianeta S ed è tangente alla stella, ossia R’S. Chi si trova lungo questa direzione assiste proprio a un contatto istantaneo del pianeta S con la stella A. Basterebbe inclinare un po’ di più questa direzione verso il basso e il pianeta S non toccherebbe più la stella e addio transito! Qual è allora l’angolo limite per il sistema stellare che vogliamo osservare? Facilissimo a dirsi e a disegnare: l’angolo Δ tra la direzione L’R’ e l’equatore della stella (dove risiedono per definizione tutti i suoi pianeti). Ovviamente, si ha una situazione del tutto analoga ribaltando la situazione nella parte alta. In questo caso la direzione è  individuata da RS ed è indicata da L. Da L vediamo il pianeta toccare la stella nel suo estremo inferiore; da L’ vediamo una configurazione identica, ma nella parte alta. Per noi, comunque, è la stessa cosa: non facciamo differenze tra alto e basso (che non esiste nell’Universo). L’angolo RAS  è, quindi, uguale a R’AS.

Per comodità di disegno, tracciamo le due linee azzurre che partono dal centro della stella A. L’angolo che esse formano rispetto all’equatore è, ovviamente, identico a Δ. Non fatemelo dimostrare… abbiamo di fronte angoli alterni interni tra rette parallele (L’R’ e L’A), tagliate da una trasversale (AS). Come ben sappiamo, essi devono essere uguali. So che è del tutto inutile, ma fatemi aggiungere un piccolo commento. Ho definito due rette parallele con un punto in comune (L’). Com’è possibile? Beh… ormai siete esperti! Quel punto L’ è un punto che può essere considerato all’infinito, dato che la distanza dell’osservatore è enormemente più grande della distanza pianeta-stella e del raggio della medesima. Possiamo, quindi, tranquillamente considerare parallele le linee che provengono da un osservatore lontanissimo. Avete visto come vengono utili le “lezioni” sul punto all’infinito del nostro piccolo corso di matematica?

Torniamo a noi e consideriamo il triangolo rettangolo verde AR’S (ma potevamo anche prendere ARS).  Di questo triangolo, che è rettangolo dato che R’ è il punto di contatto della tangente al cerchio e quindi forma un angolo retto con la direzione R’A, conosciamo un cateto (r) e l’ipotenusa (d). Che cosa vogliamo ricavare? Beh… semplicissimo: l’angolo limite di visibilità, ossia Δ.  Non ci spaventiamo di certo, dopo aver già introdotto le funzioni trigonometriche più semplici. Ricordate la definizione di seno di un angolo? Beh… ve lo ripeto: il seno dell’angolo Δ è dato dal rapporto tra ipotenusa e cateto opposto all’angolo. Possiamo quindi scrivere:

sin (Δ) = r/d

Conosciamo r e d e quindi è immediato calcolare l’angolo Δ. Conoscendo il seno, si sa anche qual è l’angolo il cui seno è il rapporto r/d. Al limite, potete usare un’obsoleta calcolatrice tascabile… ve lo concedo.

Guardiamo ancora, per un attimo, la Fig. 4, dove, come già detto, abbiamo tracciato le due rette azzurre che individuano le due direzioni limite da cui si riesce ancora a vedere (anche se al pelo) un transito del satellite più esterno. L’angolo tra equatore e le due rette è, per costruzione, proprio Δ. Cosa possiamo concludere con un semplicissimo ragionamento? Beh… se l’osservatore è meno inclinato, rispetto all’equatore, dell’angolo Δ non ha problemi a vedere i transiti. Se invece è inclinato di un angolo maggiore di Δ, non riesce assolutamente a vedere il transito del pianeta S.

Ovviamente, se abbiamo a disposizione Super Kepler, anche quest’ultima configurazione non ci spaventa: basta farlo girare e prima o poi arriverà nei famosi punti trovati la volta scorsa, ossia nei nodi della sua pseudo-orbita con l’equatore della stella. Ma basta anche molto meno. Avevo promesso, però, di non usarlo più (almeno per adesso) e quindi torniamo alla Fig. 4 e alle sue conclusioni.

Qualcuno potrebbe dirmi: “Ti piace vincere facile! E’ ovvio che hai risolto il problema. Sei partito sapendo sia il raggio della stella che la distanza dei pianeti. Ma Kepler queste cose non le sa assolutamente!”. Ovviamente, avrebbe ragione… ma a noi, per lo scopo dell’articolo, interessa fare il procedimento inverso rispetto a quello che esegue Kepler. Lui osserva i transiti (quando li osserva) e in base a ciò che vede riesce più o meno a calcolare la geometria del sistema stellare. Noi, invece, sappiamo in anticipo la geometria del sistema stellare e vogliamo scoprire dove si deve trovare l’osservatore per assistervi. Ricordiamoci, infatti, che siamo partiti dalle stelle, ma vogliamo arrivare a Giove (e magari anche agli altri pianeti) e ai suoi satelliti. In questo caso conosciamo perfettamente le configurazioni orbitali!

Prima di trasferirci nel Sistema Solare, cerchiamo di fare gli astronomi seri. Un passo in più (forse non del tutto necessario) che permette, però, una descrizione più gestibile e più vicina a quella che viene eseguita dai professionisti e poi data in pasto ai servi “calcolatori”. Noi vogliamo giungere a quel punto e non certo limitarci a quello che ci viene propinato dai programmini  a "scatola chiusa” che vogliono solo stupirci con effetti speciali, ma che non spiegano assolutamente niente. Proprio come i media, che ci assillano da tutte le parti, queste “pappe pronte” creano spesso molta confusione e molto siti web se ne cibano a occhi chiusi, senza capirne i concetti, commettendo così errori anche gravi (primo fra tutti proprio Wikipedia).

Cosa vogliamo fare esattamente. Non spaventatevi… una cosa che facciamo costantemente quando guardiamo il cielo. Considerare ciò che si vede come se fosse proiettato su una sfera, la sfera celeste. Ogni stella, pianeta, galassia, asteroide, satellite, ha una posizione ben precisa su di essa. Se usassimo un nome proprio o un “nickname” per ogni oggetto celeste sarebbe un bel caos. Molto meglio dare un nome e un cognome a ogni corpo celeste che si vede (con tutti gli occhiali possibili). Dalla geometria si sa benissimo che ogni punto di una sfera può essere individuato da un paio di coordinate, in un certo sistema di riferimento.

Lavorando su una sfera (e non su un piano) queste coordinate non sono segmenti rettilinei come la x e la y del piano cartesiano (che ormai conosciamo molto bene), ma degli archi di cerchio. Abbastanza semplice, in principio. Bisogna però definire il sistema di riferimento. Per le coordinate cartesiane si usava un punto origine e due assi perpendicolari tra loro. Per la sfera celeste si usano cerchi e punti di partenza particolari da cui misurare gli archi di cerchio. Non voglio farla troppo lunga e nemmeno introdurre tutti i sistemi di riferimento che si usano in astronomia (magari lo faremo in un articolo a se stante). Consideriamone quindi uno particolarmente favorevole per gli scopi dell’articolo. Dove stanno i pianeti (o i satelliti) di una stella (o di un pianeta)? Beh, lo sappiamo ormai bene: nel piano equatoriale dell’oggetto di riferimento. Consideriamo allora proprio l’equatore come cerchio fondamentale sulla sfera celeste. Una soluzione comunissima per descrivere il nostro pianeta e che porta alla definizione dei meridiani e dei paralleli. La conosciamo sicuramente molto bene. Usiamo, allora, la stessa strategia per rappresentare i risultati che abbiamo conseguito finora.

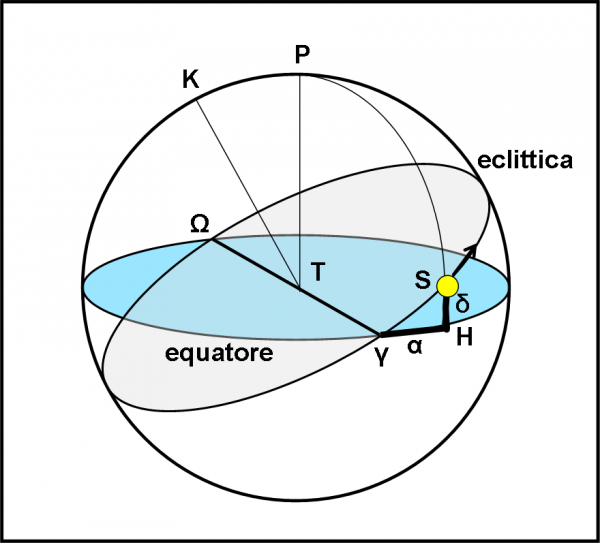
Più di tante parole vale la Fig. 5. Al centro mettiamo la stella A. Il piano di riferimento è il suo equatore (il cerchio rosso) che è stato disegnato orizzontalmente (ma potevo disegnarlo come volevo). Definito il piano equatoriale è immediatamente definito anche il polo P. Dato un punto qualsiasi Q sulla sfera celeste, esso può essere univocamente identificato attraverso due coordinate “sferiche”. La prima si ottiene tagliando la sfera con un piano passante per il polo e per l’ oggetto Q, perpendicolare all’equatore. I cerchi che si ottengono dall’intersezione di questo piano con la sfera vengono chiamati meridiani. La prima coordinata, chiamata declinazione e indicata con δ, è l’arco di circonferenza misurato sul meridiano corrispondente, che va dall’equatore al punto Q. La seconda coordinata si misura invece lungo l’equatore a partire da un punto che si può scegliere un po’ come si vuole. Per la Terra si usa spesso il punto di Ariete, quello relativo all’equinozio di primavera. Esso indica il passaggio del Sole da declinazioni negative a declinazioni positive. Per la nostra stella, potremmo scegliere uno dei nodi con la traiettoria apparente di Super Kepler.

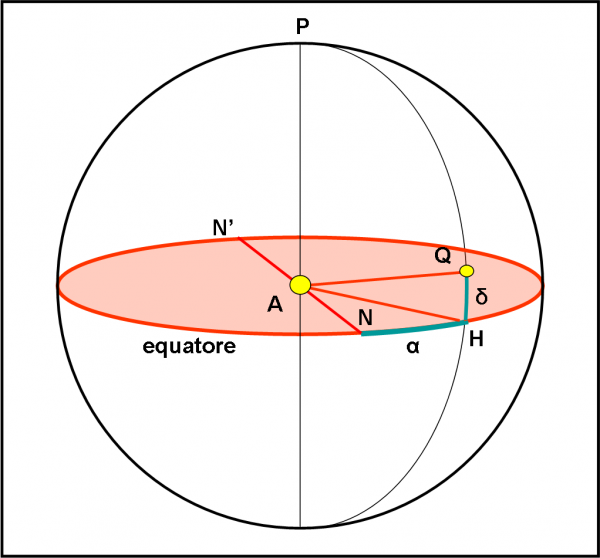
Tra breve lo faremo, ma, per adesso, non diamogli troppa importanza e consideriamo un punto N più o meno qualsiasi. L’arco di cerchio misurato lungo l’equatore da questo punto al meridiano di prima viene chiamata ascensione retta e indicata con α. Tuttavia, per adesso, poniamo l’attenzione solo sulla declinazione.

Prima di proseguire, sento di dover chiedere scusa a molti lettori  (magari a tutti). Aver descritto le coordinate equatoriali è forse stato un passaggio davvero inutile. Tuttavia, per non cadere in qualche trabocchetto nella sua applicazione più generale, ho pensato che non era male avere sottomano una definizione saputa e risaputa, ma magari mai analizzata con la dovuta attenzione. Insomma, al limite, cancellate la parte precedente…

Torniamo alla sfera celeste della stella A e alle sue coordinate equatoriali. E’ molto semplice disegnare la Fig. 6 che altri non è che la Fig. 4, “compattata” e visualizzata in tre dimensioni.  Analizziamola con la dovuta calma, dato che ci permetterà di arrivare fino a Giove e a tutti i pianeti che vorremo.

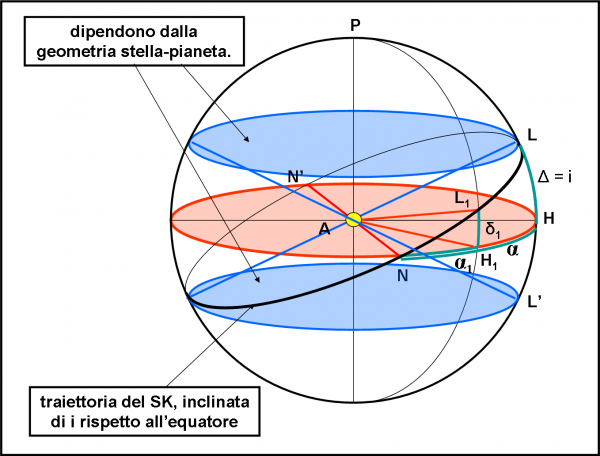
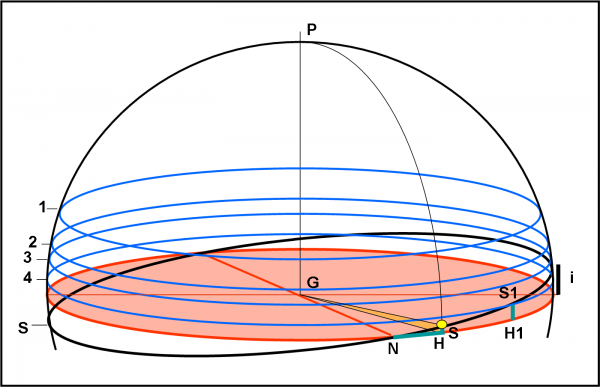
Tracciamo le due rette AL e AL’ nel piano del foglio. Esse individuano subito due “paralleli” azzurri, luogo dei punti che riescono a vedere i transiti nelle condizioni limite. Tutti questi punti hanno declinazione Δ. Limitiamoci, per semplicità, ad analizzare le direzioni L e L’, intuendo che la stessa cosa capita per ogni meridiano e per le sue intersezioni con i paralleli azzurri. E’ giunta l’ora di rimettere in moto Super Kepler e facciamolo partire dal punto L. Esso descrive un cerchio massimo, ossia un cerchio che ha centro nell’origine A. L’inclinazione i di questo cerchio nero rispetto all’equatore è esattamente uguale (per costruzione) all’angolo limite Δ. Essendo partiti da una posizione che, benché al limite, permetteva di vedere il transito più esterno “al pelo”, Super Kepler non fa che migliorare la sua osservazione (i transiti avvengono sempre più centrali). Ottiene il meglio del meglio quando arriva in N (e N’), ossia nei nodi della sua orbita rispetto all’equatore stellare. Queste considerazioni seguono perfettamente quanto descritto nell’articolo precedente. Una posizione L₁ intermedia lungo l’orbita di Super Kepler ha una certa declinazione δ₁. Avendo definito anche i nodi di quest’orbita (o pseudo-orbita come preferite), possiamo far partire l’ascensione retta α da N. L₁ ha, quindi, α₁ = NH₁ e L ha α = NH. Tanto per completezza… anche se per adesso ci interessano poco.

Direi che tutto è piuttosto chiaro. Ricapitolando: abbiamo inserito le condizioni di visibilità del transito del pianeta di un sistema stellare in un sistema di coordinate, adatto a qualsiasi trasformazione o calcolo che utilizzi la trigonometria sferica (nel caso volessimo cambiare sistema di riferimento). Ricordiamo inoltre un fatto fondamentale che non dobbiamo assolutamente dimenticare: il parallelo azzurro dipende solo e soltanto dalla geometria del sistema stellare (raggio dell’astro e distanza del pianeta più esterno) e non da altri parametri. Il cerchio massimo nero indica invece la traiettoria di SK, ossia la traiettoria di un oggetto celeste (anche se artificiale), che descrive un’orbita circolare attorno alla stella con un’inclinazione i data proprio da Δ. Questa traiettoria è molto particolare, dato che è quella che corrisponde a un caso limite, ossia a quello che vede i transiti planetari in ogni suo punto e che arriva al limite estremo (in L). Un’orbita di confine in altre parole.

Attenzione: i è un angolo fisso tra due cerchi massimi (equatore e traiettoria di SK), mentre δ è la coordinata del sistema di riferimento, variabile da punto a punto. In condizioni limite (L) la declinazione massima di visibilità Δ coincide proprio con l’inclinazione orbitale i. Ovviamente, la stessa cosa, ribaltata, capita nell’emisfero sud. Scusate la ripetizione, ma questo concetto è fondamentale per  il prosieguo dell’articolo. Ne vediamo subito una conseguenza nella Fig. 7, dove, per fare meno confusione, abbiamo eliminato la parte bassa, del tutto simile a quella alta.

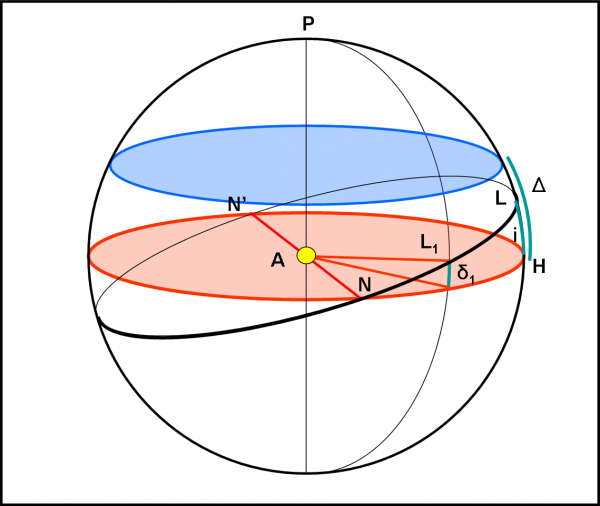
Il parallelo azzurro è rimasto tale e quale, dato che il sistema stellare è sempre lo stesso. Abbiamo cambiato, però, l’osservatore L. L’inclinazione della retta LA rispetto all’equatore è minore dell’angolo limite Δ. Questa inclinazione i è proprio quella dell’orbita di SK. Un’orbita che parte già da una posizione fortunata (benché sia la “peggiore” possibile), dato che L vede tranquillamente i transiti, essendo i (ossia la declinazione di L) minore dell’angolo limite Δ. A maggior ragione, tutti i suoi punti vedranno tranquillamente i transiti fino a ottenere il caso perfetto (equatore visto di taglio) in N. I nodi non sono cambiati rispetto a prima, dato che il nuovo L si trova sullo stesso meridiano del caso precedente.

Adesso, ridisegniamo in Fig. 8 la figura di prima (identico sistema e identico parallelo azzurro), ma per una direzione dell’osservatore L che formi una angolo i maggiore dell’angolo limite Δ (che dipende solo dal sistema stellare, ricordiamolo!). Ormai sappiamo bene come fare. La traiettoria di SK parte da un punto sfortunato (non vede i transiti), dato che i è maggiore di Δ, ma inizia a osservare il primo punto di contatto quando giunge in L₁. Non ci dobbiamo certo stupire che L₁ abbia declinazione δ₁ proprio uguale a Δ. Il parallelo azzurro, proprio perché è un parallelo, deve mantenere la stessa declinazione, essendo “parallelo” all’equatore.

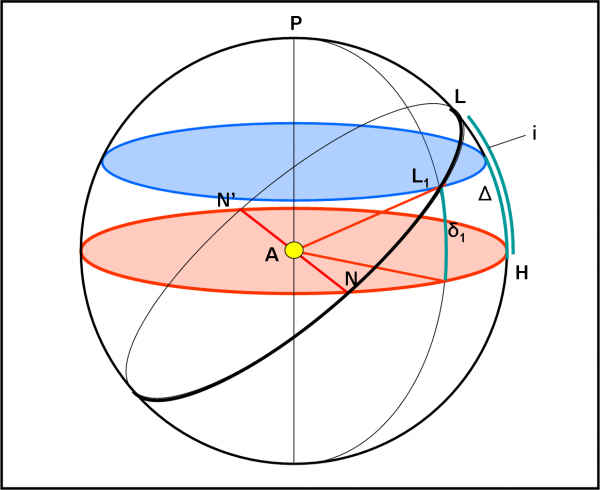
Cari ragazzi, sto dicendo cose che potrebbero sembrare delle novità. Assolutamente no. Non faccio altro che descrivere meridiani e paralleli… Pensateci bene. Sto applicando ovvietà, conosciute da tutti, a una situazione particolare. Tutto qui… e senza nessun bisogno di Celestia o “pappe pronte” del genere… Eppure, abbiamo già in mano tutti i parametri che ci permetteranno di applicare la situazione al sistema di Giove e non solo. In particolare, le coordinate che abbiamo utilizzato ci forniscono i dati esatti affinché un computer ottenga risultati del tutto professionali.

Non pensate che ce l’abbia con certe rappresentazioni pseudo-tecnologiche per partito preso. Sono convinto che siano utilissime, ma solo dopo aver compreso come funzionano le cose. Purtroppo, spesso e volentieri, si utilizzano “invece di” e non “dopo”. Le conseguenze sono molte volte una grande confusione, varie inesattezze e l’idea che certe cose siano possibili solo agli addetti ai lavori. Continuerò a lottare per dimostrare che con un po’ di fatica mentale (sicuramente anche divertimento per la maggior parte di voi) la realtà è molto più semplice di quanto si pensi.

Torniamo a noi… Cosa dobbiamo fare per passare al nostro Sistema Solare? Cambiare il ruolo della stella e di SK. La stella e i suoi pianeti diventano Giove e i suoi satelliti, mentre SK non è altro che, nel primo caso che tratteremo, un oggetto celeste “naturale” molto ben conosciuto: il Sole!

3. Spostiamo baracca e burattini

Il Sole è un Super Kepler che ha una sua “rotta” prefissata, non può cambiarla, ma riesce a osservare tutti i sistemi dei suoi pianeti. Oltretutto, seguendo la famosa traiettoria circolare attorno a loro, avrà sempre due punti in cui vedrà il piano dei satelliti di taglio (i famosi nodi).

Quello che abbiamo imparato in giro per lo Spazio, possiamo adesso applicarlo pari pari all’interno del Sistema Solare, utilizzando il Sole come telescopio spaziale. Ci occupiamo di Giove e dei suoi quattro satelliti medicei se non altro perché sono tutti ben visibili, ma il discorso cambierebbe ben poco se andassimo su Saturno o su Urano o su Nettuno (e perché no sulla Terra e la Luna). Ciò che cambia sono le caratteristiche geometriche del sistema che vogliamo studiare. In particolare, come abbiamo visto nei due articoli precedenti, il diametro del pianeta e la distanza dei satelliti dal loro “comandante”. In altra parole, dobbiamo sostituire la stella con il pianeta scelto e i suoi pianeti con i satelliti. Tutto qua. Le operazioni da fare le sappiamo molto bene e ce le hanno spiegate le Fig. 4-8. Basta aggiornarle.

La situazione che ci troviamo di fronte è quella della Fig. 9. Al centro c’è Giove e attorno a lui rivolvono quattro satelliti a distanza crescente. In questo caso vogliamo studiare le eclissi (o transiti o occultazioni, poco importa il nome) di tutti e quattro i satelliti. Ne segue che dobbiamo ricavare quattro angoli limite, uno per ogni satellite, dato che se non cambia il raggio di Giove, cambia però la distanza tra satellite e pianeta. La formula la conosciamo bene (ed è l’unica che ho introdotto e che introdurrò). Utilizziamo, ovviamente, il sistema di riferimento che già abbiamo usato con successo, ossia quello che vede come piano “fondamentale” l’equatore di Giove che possiamo ancora una volta considerare il piano in cui rivolvono tutti e quattro i suoi satelliti. Di conseguenza avremo come coordinate le declinazioni e ascensioni rette. Possiamo chiamarle tranquillamente “giovicentriche”. In altra parole, analizziamo la faccenda da Giove, come abbiamo fatto per le stelle.

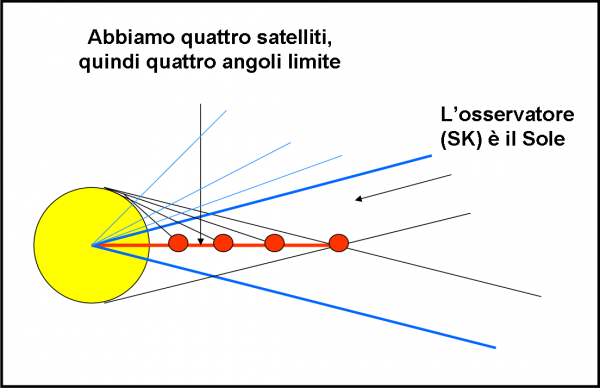
A differenza di Kepler e di Super Kepler, questa volta conosciamo tutti i parametri che possono interessarci: il raggio del pianeta e la distanza dal pianeta. Ci vuole, quindi, un attimo per calcolare la declinazione limite che permette ancora di osservare dal Sole il transito di un satellite davanti a Giove. Come già detto, ne dobbiamo calcolare quattro, dato che quattro sono i satelliti, ossia Io, Europa, Ganimede e Callisto. I risultati del banale calcolo richiesto dalla formuletta che esiste tra raggio, distanza e angolo massimo, sono riportati nella parte alta della Fig. 10.

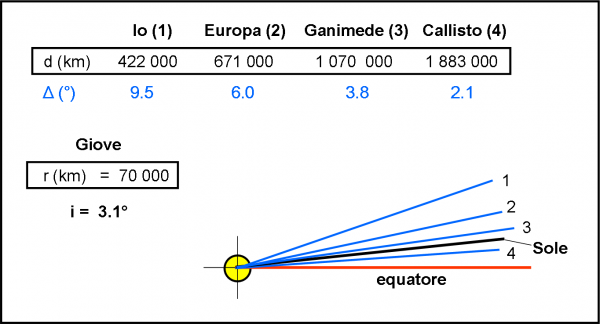
Come vedete, si hanno angoli via via più piccoli a mano a mano che il satellite si allontana. Beh… risultato più che ovvio ricordando la formula o anche solo guardando la Fig. 9.  Con questi dati in mano possiamo facilmente disegnare una figura come la Fig. 6 o 7 o 8, in cui, al centro della sfera celeste, c’è Giove con il suo piano equatoriale e in azzurro i “paralleli” che hanno come declinazione quella limite, relativa a ogni satellite.

Un momento, un momento… abbiamo tutto pronto, ma ci manca ancora l’osservatore, ossia il Super Kepler da inserire con la sua orbita nella stessa figura. No, non me ne ero dimenticato. Come già detto precedentemente la parte di Super Kepler la fa il Sole. D’altra parte è proprio perfetto per lo scopo, dato che si muove rispetto a  Giove proprio su un piano che ha una certa inclinazione i rispetto all’equatore gioviano. In realtà, avviene il contrario, ma , dato che l’orbita e circolare e avviene sempre su uno unico piano, possiamo benissimo ribaltare la situazione mettendo Giove al centro (lo facciamo sempre anche tra la Terra e il Sole…). Nella Fig. 10, non ci resta allora che inserire la linea nera che è la direzione del Sole visto da Giove al momento della sua massima declinazione (a 90° dai nodi delle due orbite), ossia quando vale proprio  i, inclinazionetra orbita del Sole (Super Kepler) e piano equatoriale di Giove.

Questo angolo vale 3.1° e, se confrontato con gli angolo limite dei quattro satelliti, ci dice già una cosa importantissima. Qualsiasi sia la posizione del Sole, esso ha una declinazione sempre inferiore alla declinazione massima dei primi tre satelliti. In altre parole siamo nelle condizioni della Fig. 7. In qualsiasi momento il Sole può vedere transitare i tre satelliti davanti a Giove. Ovviamente, li vede solo quando essi sono nella giusta posizione lungo la loro orbita (ma questo valeva anche per la stella e Super Kepler). Diversa è la situazione di Callisto. Il suo angolo limite di vista è molto piccolo, solo 2.1°, più piccolo dell’inclinazione i dell’orbita di Giove rispetto all’equatore, ossia della declinazione massima del Sole (3.1°).

Questo fatto ci dice che per Callisto vale la Fig. 8, ossia non sempre il Sole vede il transito di Callisto davanti a Giove. Accidenti, ma è così grave? Assolutamente no. La differenza tra i due angoli è  molto piccola e basta che il Sole si sposti un poco verso i nodi N e N’ e la sua declinazione diventa più piccola di quella relativa alla visibilità di Callisto. Tutte queste parole, le ho riassunte nella Fig. 11, dove vi sono i  paralleli azzurri dei quattro satelliti e il percorso nero del Sole (SK). Come si vede molto bene, basta che il Sole si trovi prima di S₁ e i transiti sono assicurati anche per  Callisto. Per gli altri tre non esistono problemi, come già detto precedentemente.

Bene, la Fig. 11 permette, se disegnata con tutta la precisione possibile, di risolvere istante per istante le condizioni di transito dei satelliti davanti a Giove. Ovviamente, tenendo  anche conto della loro rivoluzione attorno al pianeta. Fortunatamente, oggi, si conoscono perfettamente tutti i parametri in  gioco e, quindi, la previsione di questi fenomeni è un lavoro di routine che può fare benissimo il “servo” computer e i programmini che costruiscono le figure di volta in volta. L’importante, però, è che noi siamo riusciti a capire perfettamente cosa succede e perché. Non vi è dietro nessun mistero dinamico o meccanismo complicatissimo. Assolutamente no. Ci sono solo calcoli noiosi e ripetitivi che qualsiasi computer può fare. Anzi, il computer può anche tenere conto di piccole imperfezioni del nostro semplice modello.

Ad esempio, l’orbita di Giove non è perfettamente circolare così come non lo sono nemmeno quelle dei satelliti attorno a lui. Inoltre, ogni orbita ha un’inclinazione leggermente diversa e non esattamente coincidente con l’equatore del pianeta. Piccolezze che non toccano il concetto base. Leggere variazioni da inserire nelle formule da dare in pasto al calcolatore. Non vale la pena perdersi dietro a queste sciocchezze (almeno… per il nostro scopo).

Ricapitoliamo la situazione, ripetendoci ancora una volta. La situazione esistente tra satelliti, Giove e Sole, nel momento in cui quest’ultimo tocca S_1, è riportata nella Fig. 12 (parte alta). Ovviamente, per definizione, la direzione di S₁ forma proprio l’angolo limite di Callisto con il piano equatoriale (la linea azzurra di (4) coincide con la direzione del Sole). Vogliamo vedere cosa succede se ci spostassimo di 90°, ossia ci portassimo nel piano perpendicolare a quello della figura? Facilissimo: basta disegnare delle ellissi il cui semiasse maggiore è proprio il semiasse dell’orbita satellitaria, mentre il semiasse minore è dato dalla distanza dall’equatore delle intersezioni delle righe sottili (parallele alla direzione del Sole) proiettate sul piano AA’. Normalmente ciò che si vede è Giove al centro e i quattro satelliti nelle posizioni verdi (parte bassa della figura). Basta, però, aspettare e uno alla volta i satelliti transiteranno davanti a Giove, occupando le posizioni rosse. Sarebbe bello vederli tutti e quattro allineati come in figura? Sì, bello e … impossibile. Sia perché bisognerebbe avere una fortuna incredibile, che il tempo di vita del Sistema Solare non ci permetterebbe, ma -soprattutto- perché, come sappiamo bene, i primi tre satelliti di Giove sono in risonanza tra di loro (andate a rileggervi l’articolo sulle risonanze planetarie) e ripetono continuamente le stesse configurazioni, che non ammettono quella della figura…

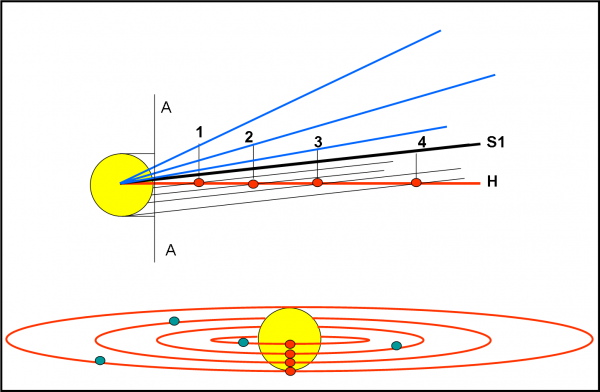
Non ho mai parlato di altre situazioni altrettanto (o quasi) interessanti. Parlo della scomparsa dei satelliti dietro a Giove. Se avete capito quanto detto finora, queste configurazioni sono estremamente banali e le lascio tranquillamente a voi…

Prima di procedere, volevo farvi notare un dato di fatto. Una figura come la parte bassa di Fig. 12 si può disegnare con foglio e matita in modo abbastanza accurato. Basta sapere la declinazione giovicentrica del Sole (ossia la declinazione eliocentrica di Giove, cambiata di segno… ridicolo!) e le dimensioni delle orbite dei satelliti. Lo schiacciamento delle ellissi la ricavate dalla parte alta, cambiando la declinazione di Giove. Veramente un gioco da ragazzi… altro che celestia o cose del genere. Potete ottenere le stesse figure da soli, con una precisione “grafica” del tutto comparabile. Quando leggete che certi programmi fanno cose mirabolanti, che sono superiori alle nostre capacità, non credeteci! Sono solo modi per mettere la polvere sotto al tappeto e non aver voglia di ragionare un poco con la propria testa…

Ben diverso è, invece, voler sapere al decimo di secondo (o anche meno) l’inizio o la fine di un transito e la perfetta geometria. In quei casi non c’è foglio e matita (ma nemmeno celestia) che tengano. Dobbiamo far lavorare il nostro schiavetto computer o andare a cercare i dati nelle tabelle già predisposte e che si trovano un po’ ovunque sul web. Se poi, volete veramente sapere cosa c’è dietro ai dati che servono al computer vi invito a dare un’occhiata QUI. Ma questo “trattato” non lo usano nemmeno celestia & co. In esso sono riportati circa 700 coefficienti correttivi che servono a definire la posizione dei quattro  satelliti rispetto ad un sistema di riferimento giovicentrico (quello che usiamo noi). Dopo la manipolazione di ben quattro matrici di rotazione, si perviene alla conoscenza delle loro posizioni viste dalla Terra e quindi al calcolo delle occultazioni/eclissi reciproche. Le posizioni sono geocentriche in quanto sono irrisori i cambiamenti temporali del fenomeno, anche per osservazioni dalla superficie terrestre, come in realtà avvengono. Gli algoritmi sono pertanto utilizzabili per qualsiasi osservatore in ogni parte del mondo. Inoltre, se si vuole andare oltre, bisogna anche tenere conto degli effetti relativistici che la massa di Giove introduce sulla luce dei satelliti che viaggia verso di noi. Meno male che ci sono gli schiavetti…

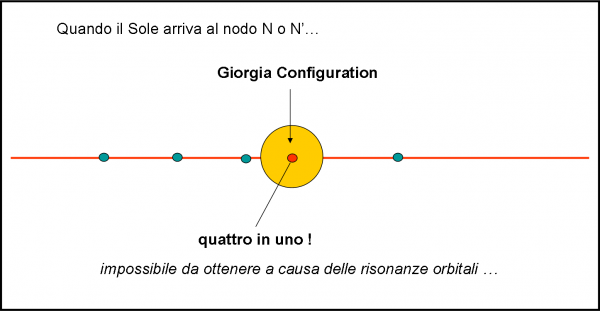
Prima di concludere questo terzo capitolo (che non è certo l’ultimo), un dovuto pensiero a Giorgia che ama molto questo tipo di articoli e si mette subito al lavoro… Se volessimo disegnare la situazione nel punto N (o N’) della traiettoria apparente del Sole, quello che vedremmo è rappresentato nella Fig. 13. Il piano equatoriale diventa una retta e i satelliti si muovono su di essa, avanti e indietro. Nasce così (teoricamente) la configurazione che ho dedicato a Giorgia (Giorgia Configuration), dato che l’aveva già preannunciata nel suo commento. Quattro per uno e uno per quattro, proprio come i moschettieri!

E' ora di fare il passetto  verso il microcosmo, sostituendo Giove con i suoi satelliti, e andando a vedere cosa sono capaci di fare tra di loro. Il Super Kepler è sempre lo stesso, ossia il Sole.

4. Giorno per giorno…

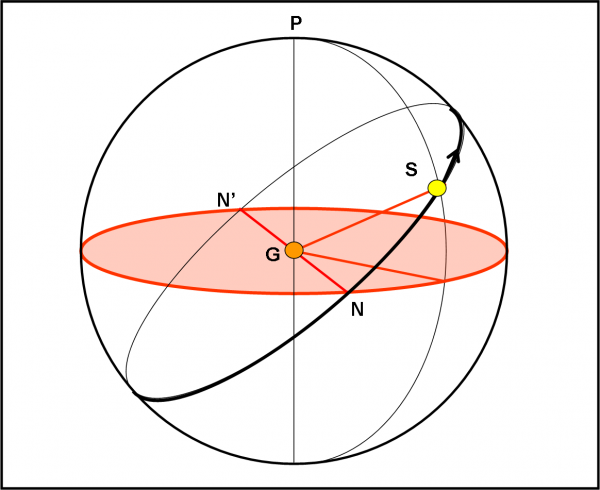
Le figure utilizzate fino ad ora sono estremamente utili, dato che permettono di calcolare immediatamente la declinazione del Sole rispetto all’equatore di Giove e, confrontandola con il valore limite di visibilità dei vari transiti satellitari, sapere se il nostro Super Kepler naturale stia compiendo osservazioni fruttuose. In qualche modo, però, siamo più che rilassati, dato che qualsiasi siano le condizioni momentanee, sappiamo benissimo che prima o poi il Sole arriverà ai nodi N e N’ e potrà vedere l’equatore di Giove “di taglio”. Sto parlando, ovviamente, delle figure come la Fig. 11, dove i punti sicuramente utili sono proprio N e N’.

Cosa ci dice questa ovvia constatazione? Un fatto importantissimo che spesso porta a grandi confusioni in chi cerca di spiegare senza avere capito veramente la problematica. L’inclinazione dell’orbita di Giove rispetto all’equatore gioviano ha un’importanza abbastanza relativa. Nel senso che se fosse troppo alta si potrebbero osservare i transiti solo avvicinandosi ai nodi N e N’. Vi ricordate cosa abbiamo detto nel primo capitolo? Potrebbe anche essere inclinata di 90°, ma due punti fortunati per vedere i transiti l’avremmo sempre e comunque.

Il fatto che l’orbita sia inclinata di soli 3° è, però, sicuramente un vantaggio in più, perché permette di vedere i transiti dal Sole lungo quasi tutta la sua orbita. Notate, inoltre, che dell’inclinazione dell’orbita gioviana rispetto all’orbita terrestre non abbiamo assolutamente parlato. E ne parleremo ben poco, dato che la sua importanza è ancora più relativa, malgrado si legga in giro che è proprio questa inclinazione molto piccola  a permettere i fenomeni mutui. Assolutamente no, come vedremo…

Torniamo al nostro SK solare. Le rappresentazioni usate nelle figure precedenti ci ricordano qualcosa che usiamo spesso e volentieri per la nostra Terra. Infatti, quando disegniamo sulla sfera celeste l’equatore terrestre e l’eclittica identifichiamo, immediatamente, le stagioni. Il nodo ascendente è il punto d’Ariete (γ), dove comincia la primavera e quello opposto il punto della Bilancia (Ω) dove inizia l’autunno. Nei due punti a 90° si hanno i solstizi. Insomma, quella figura ci indica chiaramente che nei nodi il Sole passa da declinazioni negative a positive e viceversa. Nei nodi, ovviamente, l’equatore è visto di taglio dal Sole e la durata del giorno e della notte sono uguali dappertutto. Cose ben note e quasi ridicole. Tuttavia, fatemi disegnare la situazione “terrestre” nella Fig. 14.

Essa può facilmente essere trasformata in un diagramma ancora più leggibile e facilmente utilizzabile. Il Sole compie un giro completo sulla sfera celeste (da nodo ascendente a nodo ascendente, ad esempio) esattamente in un anno, ossia in 365 giorni circa. Possiamo anche dire che, in prima approssimazione, il Sole percorre la sua traiettoria sulla sfera celeste a velocità costante (orbita circolare). Esiste quindi un legame semplice e diretto tra ascensione retta e tempo. La prima compie i suoi 360° (o se preferite 24 ore), il secondo l’anno.  Diventa quindi banale trasformare la nostra sfera celeste e tutti i suoi archi ed archetti che comporterebbero la conoscenza della trigonometria sferica, in un diagramma disegnato su un piano, attraverso delle coordinate cartesiani, nostre care amiche.

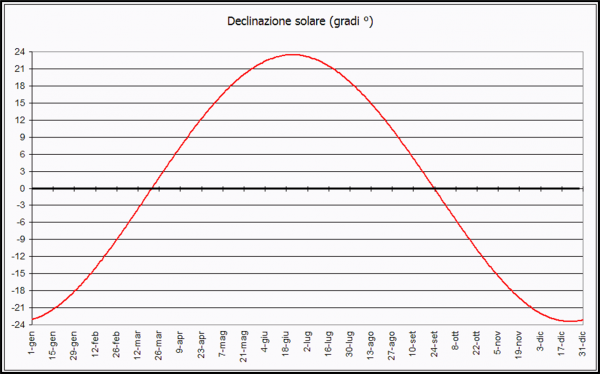
L’ascensione retta si può trasformare tranquillamente in tempo, misurato in mesi, giorni, ore, ecc., la declinazione resta quella che è. In ascissa mettiamo il tempo e in ordinata la declinazione geocentrica del Sole. Otteniamo la Fig. 15, di immediata comprensione. Una bellissima sinusoide (vedi funzioni trigonometriche nella sezione matematica…). Dove essa taglia l’asse delle ascisse si trovano i nodi, ossia gli equinozi (declinazione uguale a zero); dove raggiunge il massimo e il minimo vi sono i solstizi. Una figura comodissima che permette di trovare graficamente la posizione del Sole, rispetto all’equatore, in ogni momento dell’anno. Notate che il massimo (e il minimo) valgono proprio i famosi 23° dell’inclinazione dell’orbita terrestre. Cosa che le figure dei primi capitoli dovevano già farci intuire da molto tempo.

Perché non usare la stessa figura anche per Giove? Le figure usate finora sono proprio dello stesso tipo, come dimostra lo schema di massima mostrato in Fig. 16 (è un’ennesima ripetizione, ma meglio averla sempre vicina). Bisogna solo ricordare che il Sole gira intorno a Giove (o il viceversa) non in un anno terrestre ma in un periodo un po’ più lungo, ossia in quasi dodici anni terrestri (11.86). Problema insignificante, dato che possiamo continuare a utilizzare i giorni e i mesi terrestri. La sinusoide di Giove si chiuderà solo dopo un periodo più lungo, ma tutto il resto rimane analogo.

Tracciamo in Fig. 17 la Fig. 15 terrestre, riferita questa volta a Giove. Il tempo è ovviamente espresso in giorni terrestri (per comodità). Si notano i due nodi (dove il piano equatoriale viene visto di taglio) e il massimo e il minimo che raggiungono a malapena i 3.1° di declinazione giovi centrica (proprio l’angolo tra orbita gioviana e il suo equatore). Questa figura non fa altro che rappresentare le stagioni di Giove! Tuttavia, a noi non importano le stagioni, ma i transiti dei satelliti.

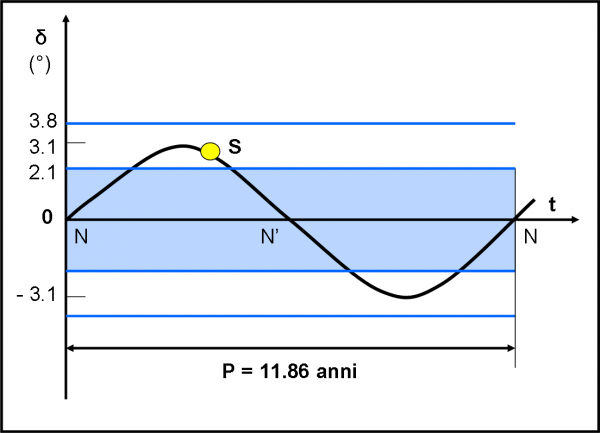
E’ immediato, allora, disegnare nella stessa figura anche quei famosi “paralleli” azzurri usati nel capitolo precedente. Ricordiamo che essi sono il luogo dei punti che hanno, come declinazione, quella limite relativa a ogni satellite. Beh… se hanno sempre la stessa declinazione, quei paralleli diventano delle rette parallele all’asse x (ossia all’asse del tempo) nella Fig. 17. Disegniamole, ovviamente, come linee azzurre. Ne ho disegnato solo due. Perché? Ma è ovvio: i primi tre satelliti si vedono dal Sole sempre con angoli minori di quello limite (ho inserito solo quello di Ganimede, pari a 3.8 gradi, trascurando Io ed Europa che sono nettamente più in alto). La sinusoide è sempre più bassa di queste tre linee. La linea di Callisto, invece, si trova un po’ più bassa e la Fig. 17 ci mostra molto bene quando il Sole la taglia. In poche parole, se il Sole si trova all’interno della banda azzurra TUTTI i transiti sono sempre visibili. Una figura veramente comoda e facilissima da usare. E, soprattutto, costruibile con foglio e matita.

Non ce ne sarebbe bisogno, ma fatemi fare una “sciocca” precisazione. Stiamo sempre parlando di Sole che osserva i transiti. La situazione è, però, identica a quella di Giove che vede il Sole occultato dai suoi satelliti. Posso permettermi di stare su Giove e pensare a quello che vede il Sole proprio per questa possibilità di scambio dei ruoli. Capita lo stesso anche per una stella, un suo pianeta e Kepler. Se Kepler vede un transito di un pianeta davanti alla stella, esiste sicuramente una zona della stella da cui si “vedrebbe” il pianeta passare davanti a Kepler…

E’ comunque giunta l’ora di abbandonare il nostro telescopio naturale. Ci siamo accorti che fa troppo caldo e che le osservazioni eseguite dal Sole sono veramente difficili (specialmente d’estate… ah ah ah…). E’ un vero peccato, perché è su una traiettoria ideale per assistere ai transiti…

Un attimo, un attimo… il Sole non è solo un osservatore “passivo”, ma è un  osservatore  “attivo”. Super Kepler deve sperare nella luce della stella che viene bloccata dal suo pianeta, ma il Sole è capace di inviare luce e molta di più di quella che è capace di emettere Giove (che poi non fa altro che sfruttare quella del Sole attraverso la riflessione…). Accidenti, è vero! Se Maometto non va alla montagna, la montagna può andare da Maometto. Invece di usare il Sole come osservatore e basta, utilizziamolo proprio come stella (speriamo che non si sia offeso…).

Tutta la trattazione che abbiamo fatto finora, però, non cambia di una virgola. Dobbiamo solo cambiare il modo di “dire” le cose. Un transito di un satellite davanti a Giove visto dal Sole, diventa un’eclisse di Sole su Giove da parte del satellite. La luce viaggia, in prima approssimazione, in modo rettilineo e quindi ciò che vede il Sole può essere considerato ciò che il Sole invia verso Giove. La Fig. 18 illustra, banalmente, la nuova situazione.

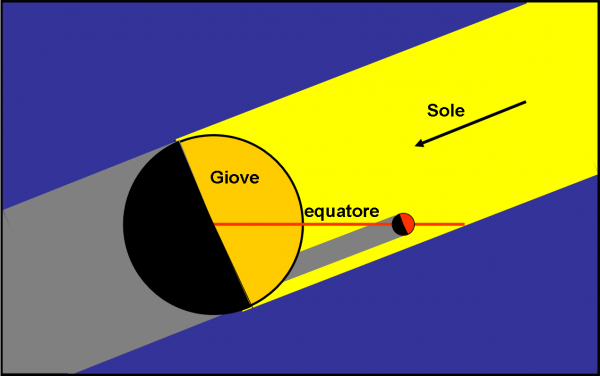
L’importante è che la Fig. 17 (e quelle precedenti) restino invariate e continuino a essere valide per i nostri scopi. Invece di dirci quando e come il Sole vede i transiti, ci dicono, adesso, quando e come l’ombra dei satelliti, dovuta alla luce solare, si proietta sul pianeta. Insomma, ci dicono quando capitano le eclissi di Sole causate dai satelliti medicei.

Qualcuno mi dirà: “Va bene, abbiamo evitato il caldo del Sole… ma non è che andare su Giove sia molto meglio. A parte i costi, è difficile camminare sulla sua atmosfera…”. No, no, non c’è bisogno di andare su Giove. Mentre un transito è qualcosa che necessita la presenza fisica sulla linea in cui avviene (vedi SK), un’eclissi può essere vista anche da altre posizioni. Ciò che interessa è vedere quella macchiolina nera dovuta all’ombra del satellite… Questo è il grande vantaggio delle eclissi!

Come facciamo a sapere da dove si possono vedere le eclissi di Sole su Giove? Basta usare, nuovamente, carta e matita e fare un disegno a dir poco elementare. Utilizziamo la Fig. 19.

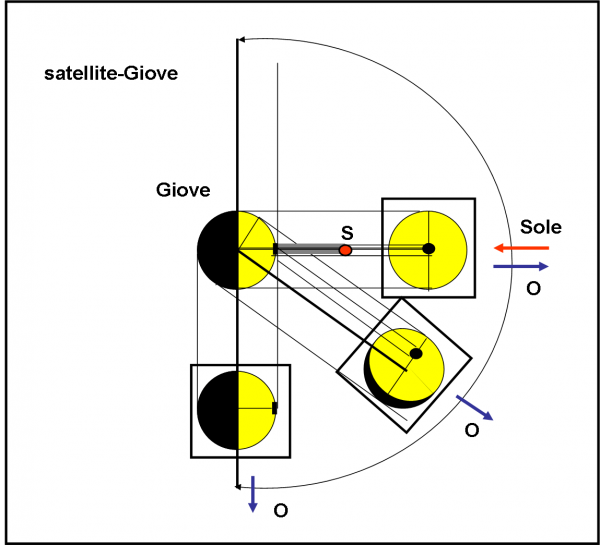
Immaginiamo che il piano del foglio sia quello perpendicolare al piano che contiene Sole, satellite e Giove. Possiamo anche considerare, più semplicemente, che esso sia proprio il piano equatoriale di Giove, tanto la situazione finale non cambia. La luce del Sole proviene orizzontalmente da destra (freccia rossa). Il satellite S la intercetta e causa il cilindro d’ombra (parliamo di cilindro e non di cono, dato che il Sole è abbastanza lontano da Giove rispetto alla distanza dei satelliti) che proietta la macchia nera sul disco planetario. Dove bisogna trovarsi per poter vedere questa macchiolina? In parole povere, potrei dire: “Ovunque sia visibile l’emisfero di Giove che contiene la macchiolina”.

Sicuramente non vedrei niente se andassi dalla parte opposta di Giove rispetto al Sole. In quel caso vedrei l’emisfero in ombra. E’ facile, però, notare che la macchia è ancora visibile perfino dalla posizione perpendicolare alla direzione del Sole, sia in basso che in alto. Ossia ci si può spostare tranquillamente di un angolo di 180° senza perdere lo spettacolo. In particolare, nei due casi estremi, la macchiolina sarebbe proprio sul bordo di Giove e sarebbe praticamente un punto quasi impercettibile. Tuttavia, basta spostarsi un pochino verso il centro. Per facilitare la comprensione della situazione, ho inserito, per tre direzioni particolari, ciò che l’osservatore vedrebbe dalla rispettiva posizione. Queste tre osservazioni sono inserite nei rettangoli. Esse rappresentano il pianeta visto su un piano perpendicolare alla linea di vista. L’ombra è sempre ben visibile tranne che nel punto a 90°, dove si intuisce appena. In ogni modo, direi che non c’è proprio da preoccuparsi! Quando avviene un’eclisse (e sappiamo, dalle figure precedenti, che questo è un evento quasi continuo, tranne per quel piccolo intervallo negativo di Callisto) lo spettacolo è assicurato.

Attenzione: quello che ho disegnato sul piano del foglio vale anche per osservatori posti su un piano perpendicolare al foglio o su qualsiasi piano che passa per la direzione Sole-Giove, dato che la geometria è identica. In questo enorme emisfero di visibilità ci sta tranquillamente anche la Terra, ovviamente…

Non vogliamo, però, ancora tirarla in ballo e continuiamo a guardare cosa succede intorno a Giove. Torniamo anche a parlare di osservatore Solare, tanto sappiamo benissimo che il tutto può essere ribaltato considerando i transiti come delle eclissi: basta che l’osservatore Sole diventi attivo e accenda la luce!

Qualcuno potrebbe dirmi: “Ti è piaciuto vincere facile!” Avrebbe anche ragione. In fondo, Giove è enorme rispetto ai suoi satelliti, che gli sono anche molto vicini. Oltretutto, il piano orbitale di Giove è inclinato di pochissimo rispetto all’equatore del gigante. Tutte queste caratteristiche hanno permesso una visione continua dei fenomeni mutui tra satelliti e Giove, sia se li chiamiamo transiti, visti dal Sole, sia se li chiamiamo eclissi, visti da Giove (o da osservatori distribuiti un po’ ovunque nello spazio “teatrale”). In realtà, di mutuo c’è stato ben poco finora. Beh…sì, è colpa mia che non vi ho mai parlato della scomparsa dei satelliti dietro a Giove. Se ragioniamo sui sistemi planetari stellari, questi eventi sarebbero le eclissi secondarie, ossia quelle relative al passaggio del pianeta dietro alla stella. Scientificamente sono molto interessanti, comunque, ma sono di ben più facile trattazione e li lascio a voi. Può essere un ottimo esercizio per controllare se avete capito bene tutta la strategia grafica.

Per non far diventare questi articoli una specie di Divina Commedia (come lunghezza, ovviamente…), inseriamo, invece, una difficoltà in più, in modo che non mi possiate accusare di “vincere facile”. Andiamo ad analizzare qualcosa di molto meno frequente, ossia le occultazioni o transiti o eclissi tra i satelliti di Giove. Il pianeta non interessa più, ma interessano solo i suoi quattro figlioli. Mamma mia, che problema gigantesco… Forse c’è proprio bisogno di … Celestia & Co. No, assolutamente no. Potreste risolvere il tutto da soli, dato che non dovete fare altro che ripetere pari pari quanto fatto finora, cambiando solo il raggio di Giove e la distanza dei satelliti. Tutta la strategia grafica e logica restano uguali e i risultati sono di facilissima interpretazione.

5. Restringiamo Giove e il concetto non cambia…

Nei capitoli precedenti, abbiamo descritto le condizioni in cui dal Sole si può vedere il transito dei satelliti medicei sul disco di Giove. Sono bastati un pizzico di trigonometria -e tanti disegni- per stabilire una regola base, applicabile a tutti i sistemi satellitari del Sistema Solare e non solo. Siamo anche riusciti a rappresentare la situazione sulla sfera celesta giovicentrica e a descrivere istante per istante la posizione dell’osservatore Sole in modo da determinare immediatamente se un evento può o non può capitare. Facendo diventare il Sole la stella che è, abbiamo, inoltre, usato i risultati ottenuti per descrivere le eclissi mutue tra satelliti e Giove, dato che la situazione è perfettamente speculare. Abbiamo, infine, concluso che quando capita un’eclisse, essa può essere vista da una platea estremamente estesa.

Finora si sono considerati i satelliti e il disco di Giove. Abbiamo, sicuramente, giocato facile, dato che i satelliti sono molto vicini a Giove e il disco del pianeta è molto grande. La conclusione è stata che le condizioni di visibilità dei transiti visti dal Sole sono quasi sempre rispettate e, di conseguenza, anche delle eclissi di Sole viste da Giove. Non vi è nemmeno bisogno di fare girare il Sole come un Super Kepler: qualsiasi posizione è utile.

E’ venuto il momento di complicarci le cose e di fare un passo in più. Normalmente, si cerca di rivestire questo passaggio come un qualcosa di molto più complesso, che solo gli esperti possono risolvere. E, invece, non è vero. La configurazione e il procedimento rimangono gli stessi. Di cosa sto parlando? Beh… dei transiti, visti dal Sole, di un satellite davanti a un altro o, specularmente, di un eclissi di Sole vista da un satellite per colpa di un fratellino.

Cosa cambia realmente rispetto a prima? Pochissimo: invece del disco di Giove, dobbiamo considerare il disco del satellite che subisce il transito o l’eclisse, e, invece della distanza satellite-Giove, la distanza tra i due satelliti. La formuletta ce l’abbiamo già e basta inserire i parametri al suo interno per stabilire le condizioni di visibilità tra satellite e satellite. In altre parole, basta escludere Giove dal gioco. Lui continua a essere presente solo perché i satelliti sono vincolati a girare sul suo piano equatoriale e quindi a rivolvere attorno al Sole. Ne segue, quindi, che l’equatore gioviano rimane il piano di riferimento, tale e quale a prima.

Meglio di tante parole, conviene inserire una banalissima figura che spieghi la situazione. Usiamo la Fig. 20. Nella parte bassa vi sono i soliti due satelliti (1) e (2); il piano equatoriale di Giove, dove stanno i satelliti; la direzione del Sole, la cui declinazione è al massimo l’inclinazione orbitale i; la linea azzurra che è quella che caratterizza l’angolo limite del satellite (1), ossia la declinazione necessaria per essere visto transitare davanti a Giove. Insomma, proprio quello che abbiamo fatto finora e che ci ha portato a tutte le figure dei capitoli precedenti.

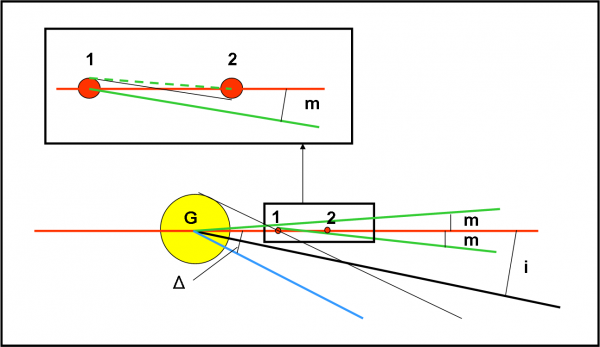
Cosa vogliamo aggiungere, adesso? Le condizioni di visibilità limite affinché il satellite (2) transiti davanti a (1) se visto dal Sole. Come vi dicevo cambia solo il diametro e la distanza… Possiamo già aspettarci il risultato. E’ vero che i satelliti sono più vicini tra loro di quanto non lo siano a Giove (almeno a due a due), ma il loro diametro è ridicolo rispetto a quello del pianeta. Ne consegue che l’angolo limite di visibilità m sarà sicuramente più piccolo di quello trattato finora. E, come conseguenza, sarà più difficile per il nostro Sole (o Super Kepler) riuscire ad assistere all’evento. Abbiamo comunque una sicurezza. Sia come sia quest’angolo limite, vi saranno sempre due punti in cui la visione sarà possibile! Ormai lo sappiamo bene: sono i due nodi tra equatore e orbita di Giove (o del Sole, come preferite). Non abbiamo perciò molta ansia a proseguire, sapendo che ci saranno sempre due configurazioni utili. E’ bello possedere un Super Kepler “naturale” come il Sole: e’ sempre una garanzia di successo.

Torniamo alla Fig. 20 e ingrandiamo nel riquadro la parte che ci interessa, ossia quella che identifica l’angolo m, il nuovo angolo di visibilità limite tra (1) e (2). Ripeto ancora che esso identifica l’angolo limite per assistere dal Sole a un transito di (2) davanti a (1). In altre parole, la declinazione del Sole deve essere inferiore a m per godersi lo spettacolo. E’ così difficile ricavare l’angolo m? No e continuano a essere sufficienti carta e matita e qualche dato che si trova dappertutto.

Eseguo solo una semplificazione (che potremmo anche non fare, ma la trattazione diventerebbe troppo lunga). Quando lavoravamo con i satelliti e Giove era più che sufficiente considerare i satelliti puntiformi rispetto al pianeta. Adesso, la situazione è leggermente diversa, dato che i diametri dei satelliti sono comparabili. Tuttavia, le distanze tra di loro sono sempre grandi rispetto al diametro e quindi gli angoli molto piccoli. Lasciatemi, perciò, continuare a considerare il satellite che deve transitare  davanti all’altro come puntiforme. Ossia, sostituisco la linea verde continua del riquadro con quella verde tratteggiata. E’ una semplificazione che ci permette di non considerare la doppia tangenza tra i due satelliti. Basterebbe cambiare un pochino la formula che ci permette di calcolare m, ma non ne vale la pena. Oltretutto, come si vede chiaramente, il nuovo angolo che trovo è più piccolo di m e quindi non faccio altro che limitare le possibilità di visibilità del transito. Insomma, vi regalo una sicurezza ancora maggiore! Non preoccupatevi, però. Come già detto, gli angoli sono piccoli e sono talmente tanti i parametri che non possiamo considerare (eccentricità dell’orbita gioviana, piani orbitali dei satelliti non perfettamente complanari, ecc.) che questa semplificazione non cambia il risultato concettuale. Tanto, come ormai sappiamo bene, l’importante è dare al computer l’idea di base. Lui sarà capace di tenere in conto tutte le sfumature. Se non fosse così perché avremmo mai dovuto inventarlo? Non certo solo per usare facebook o twitter…

Disegniamo, allora, la Fig. 21 Come vedete è perfettamente identica alla Fig. 4 (seconda parte). Vi è sempre un triangolo rettangolo e il seno dell’angolo m vale sempre il rapporto tra raggio e distanza. Trovate qualche difficoltà supplementare? Direi proprio di no. Non abbiamo fatto altro che sostituire Giove (o la stella) con un satellite e la distanza Giove-satellite (o stella-pianeta) con la distanza satellite-satellite. Elementare, Watson!

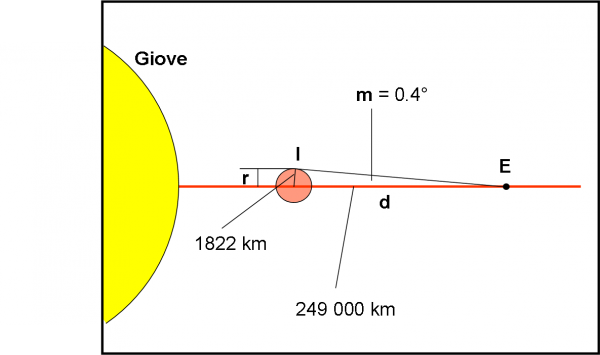
Consideriamo, ad esempio, i primi due satelliti medicei: Io (I) ed Europa (E). Ho considerato loro perché sono i più vicini e quindi danno anche l’angolo m più grande. Se il Sole ha una declinazione satellicentrica (che è però anche Giovicentrica dato che i satelliti risiedono sul piano equatoriale di Giove) inferiore a questo valore “massimo” dell’angolo limite, vi è transito mutuo tra i due satelliti.  Potremmo fare i calcoli per tutte le coppie e per tutte le possibili configurazioni di allineamento (divertitevi…). Nel caso della figura si ottiene un angolo m = 0.4°. Beh… c’era da aspettarselo, dato che le condizioni diventano molto più restrittive.

A questo punto potremmo nuovamente descrivere i paralleli azzurri per ogni coppia di satelliti e via dicendo. Ma, ormai, sappiamo bene come fare (basta seguire le figure del capitolo scorso con i nuovi risultati). Vedremmo che il Sole sta quasi sempre al di sopra dei paralleli azzurri e quindi non riesce ad assistere ai transiti con continuità. Nessun problema, basta aspettare… i nodi non tradiscono mai!

Passiamo subito all’ultima figura che descrive sinteticamente e quantitativamente la visibilità da parte del Sole. Mi riferisco a quella che riporta la declinazione solare giovicentrica in funzione del tempo (Fig. 17, quarta parte). Può bastare ritoccarla un po’ e il gioco è fatto, come mostra la Fig. 22. Il percorso del Sole è sempre lo stesso. Dobbiamo solo aggiungere la fascia verde che indica la zona in cui il Sole vedrebbe almeno un transito (in particolare, quello tra Europa e Io, pari a una declinazione limite di 0.4°). Sicuramente le cose sono cambiate e il Sole entra nella fascia quando arriva piuttosto vicino ai nodi, ossia quando assume una declinazione prossima a zero (equatore visto di taglio).

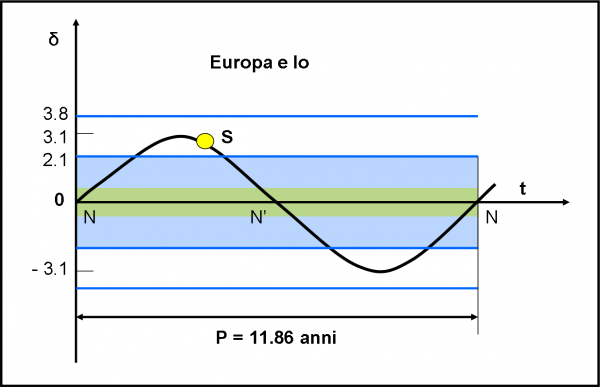
Ricordiamo, ancora, che i nodi dividono a metà il percorso completo del Sole. Dato che il Sole impiega 11.86 anni a girare attorno a Giove (o il viceversa, ma è lo stesso), ne segue che i transiti mutui tra satelliti avvengono circa ogni 11.86/2  = 5.93 anni. Dato che si ha un certo margine prima e dopo i nodi, non è certo sbagliato concludere che avvengono in media ogni sei anni circa.

Finora, abbiamo studiato le varie situazioni guardando le configurazioni in un piano perpendicolare a quello dell’equatore e dell’orbita di Giove. Quando parlavamo di transito di un satellite davanti a Giove, non vi era nemmeno bisogno di vedere le cose “dall’alto” o “dal basso” (avremmo solo capito quanto sarebbe durato il transito). Per i transiti mutui dei satelliti è invece molto più istruttivo, dato che essi orbitano attorno a Giove con periodi diversi tra loro e quindi danno luogo a configurazioni abbastanza variegate. Una precisazione ovvia, ma che non fa mai male. Il Sole si muove lungo la sua traiettoria molto lentamente e quindi una sua posizione favorevole nella Fig. 22 vuole dire regalare un’ampia possibilità ai satelliti per girare attorno a Giove, dato che i loro periodi orbitali vanno da poco più di uno a poco meno di diciassette giorni. In altre parole, il Sole aspetta che i satelliti giochino a nascondino.

Vale, quindi, la pena di mostrare ciò che capita guardando tutto perpendicolarmente all’equatore di Giove, ossia proiettando il tutto su di esso. Vediamo qualche caso, relativo a soli due satelliti, nella Fig. 23. Le due linee verdi delimitano la zona in cui possono avvenire i transiti. Come si nota si possono avere transiti di 1 davanti a 2 (1’ e 2’oppure 1 e 2’) o di 2 davanti a 1 (2 e 1’ oppure 2 e 1).

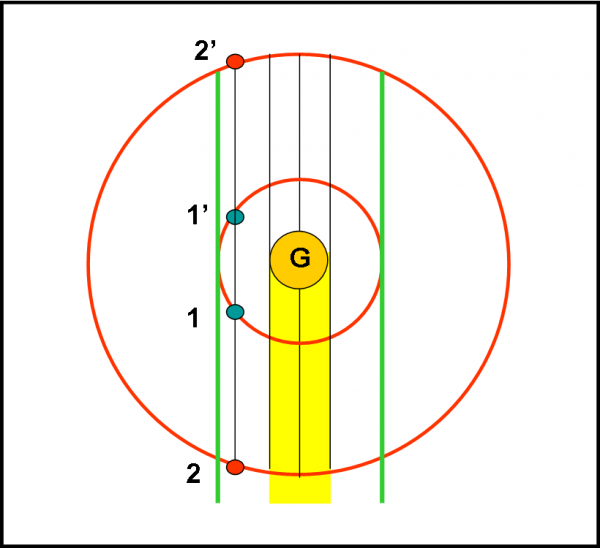
Il successo dei transiti dipende, però, anche dalla configurazione verticale (quella maggiormente utilizzata finora) e dai valori dei periodi di rivoluzione dei satelliti. Insomma, la soluzione esatta ci sarà data nuovamente dal calcolatore. Ma noi sappiamo benissimo cosa succede e questo è l’importante. Se poi vogliamo anche simulare la situazione con un programma “pappa pronta” possiamo anche farlo, dato che ormai abbiamo capito il gioco.

A questo punto, possiamo pure fare accendere la luce al nostro Super Kepler e dare al Sole quello che è del Sole. I vari transiti diventano immediatamente eclissi mutue tra i satelliti. Non ci rimane che calcolare chi li può vedere. Non cambia niente rispetto al problema Giove-satellite. Anzi, gli spettatori possono anche disporsi in posizioni più defilate. Infatti, l’ombra proiettata su un satellite da un  altro non sarà effettivamente un punto, ma un disco piuttosto grande, magari il cilindro d’ombra è perfino superiore al disco colpito. Ne segue che si estende il campo di visibilità, come mostra la Fig. 24, analoga alla Fig. 19 (quarta parte). Si notano eclissi anulari, strisce luminose e magari anche “buio totale”,  dato che il satellite investito dall’ombra è più piccolo del cilindro d’ombra (eclissi totale di Sole). Lascio a voi studiare bene la figura e le altre possibilità. Ormai è un gioco da ragazzi…

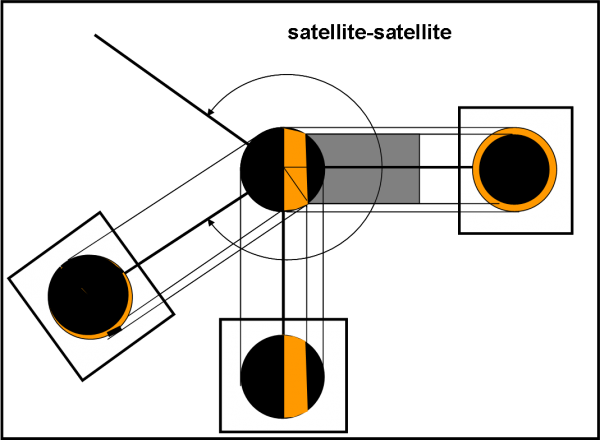
Abbiamo risolto tutti i casi di eclissi. Dobbiamo dire grazie al Super Kepler Sole, una sonda perfetta.

L’appetito, però, vien mangiando. E se cambiassimo sonda? Visto che abitiamo sulla Terra, perché non considerare proprio lei come Super Kepler? Otterremo lo stesso risultato? Purtroppo no. Per due motivi: innanzitutto perché la Terra non si può accendere e deve accontentarsi di vedere i transiti (osservatore passivo). Un fenomeno, quello dei transiti, che è del tutto “soggettivo”, dato che nessun altro può vederlo in giro per lo Spazio, tranne casi estremamente particolari. Cosa, però, ancora più importante è che la Terra non gira intorno a Giove, ma intorno al Sole. E questo complica un po’ la situazione. Chiedetelo a Tolomeo e ai suoi epicicli che cercavano di spiegare il movimento di un Giove che doveva assolutamente girare (quasi) attorno alla Terra.

6. Un Super Kepler irrequieto

Qui, sulla Terra, siamo abbastanza contenti, ma ci dispiace un poco non aver visto direttamente i transiti. Come potremmo fare? Beh… si potrebbe usare la stessa Terra come Super-Kepler costringendola a girare attorno a Giove e ai suoi figlioli. Purtroppo, malgrado la tecnologia sia ormai eccezionale, spostare la Terra a piacimento rimane ancora un problema insolubile. Dobbiamo rassegnarci? Beh… non è detto. Anche il nostro pianeta potrebbe fare concorrenza al Sole. E’, in effetti, anche lui un Super-Kepler, anche se  un po’ indipendente e bizzarro.  Si comporta come se fossimo tornati ai tempi di Tolomeo, quando gli epicicli riuscivano a spiegare i moti dei corpi planetari. Accidenti, le cose si complicano e, forse, dovremmo iniziare ad affidarci ai programmi “a scatola chiusa”… Macché, state tranquilli: basta ancora il foglio e la matita, con l’aggiunta di un pizzico di attenzione e di voglia di capire.

Vediamo qual è la situazione relativa al magnifico terzetto Sole, Giove, Terra. Finora abbiamo sempre immaginato che sia il Sole a rivolvere attorno a Giove. Abbiamo sbagliato? Assolutamente no. Lo facciamo continuamente per la coppia Terra-Sole e quindi possiamo continuare a farlo, invertendo le posizioni. Il problema, come abbiamo visto prima, è che lo stesso stratagemma non possiamo farlo direttamente tra la Terra e Giove. Tuttavia, se il Sole gira attorno Giove e se la Terra gira attorno al Sole, possiamo dire che, in modo un po’ strano, anche la Terra DEVE girare attorno a Giove.

Il nostro pianeta si fa trascinare dalla stella nel suo moto “apparente”. Non è forse quello che fa la Luna? Anche lei gira intorno alla Terra, mentre la Terra gira intorno al Sole. E’ una situazione che conosciamo molto bene. In fondo, in fondo, anche la Terra può essere considerata un Super-Kepler dato che segue il Sole, pur danzandogli attorno. Molto meglio rappresentare queste banali considerazioni in Fig. 25.

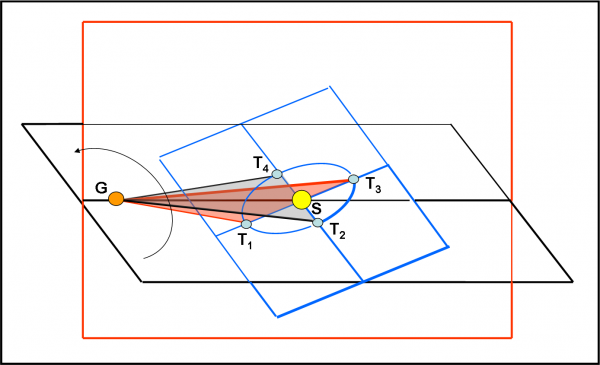
Ho disegnato i tre piani fondamentali. Quello nero (orizzontale) è il piano dell’orbita di Giove attorno al Sole, ossia del Sole attorno a Giove. Quello azzurro è il piano orbitale della Terra (eclittica), inclinato di un certo angolo rispetto a quello precedente (che è poi l’inclinazione del piano orbitale gioviano rispetto all’eclittica). Infine, quello rosso è perpendicolare al piano di Giove.

Blocchiamo con una bacchetta magica la situazione ad un certo istante della rivoluzione del Sole attorno a Giove. Lasciamo muovere solo la Terra e evidenziamo quattro punti particolari lungo la sua orbita: T₂ e T₄ non sono altro che i nodi tra l’eclittica e il piano dell’orbita gioviana; T₁ e T₃ sono invece i punti in cui si raggiunge la massima distanza angolare tra la Terra e il Sole, vista da Giove. Uno sarà “sopra” il piano di Giove e l’altro “sotto”. I due angoli non sono uguali, dato che in una caso la Terra si trova più lontana da Giove e nell’altro più vicina di quanto non sia ai due nodi. Questi due angoli sono sempre più piccoli dell’inclinazione del piano di Giove rispetto all’eclittica, dato che la distanza Terra-Sole è decisamente più piccola di quella tra Giove e il Sole.

Conoscendo le distanze dei due pianeti dal Sole e della Terra da Giove, esiste una formula trigonometrica che permette di ricavare l’angolo che ci interessa. Magari ne parleremo, ma per adesso sappiamo che si può calcolare facilmente.

Nella figura ho solo indicata con una freccia l’orbita del Sole attorno a Giove,  per non allargare  troppo il disegno.

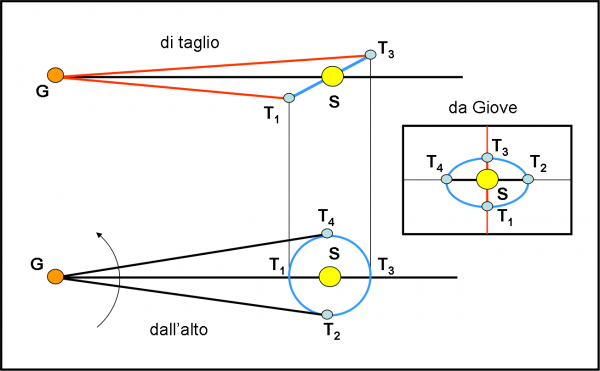
Nella Fig. 26 vediamo, adesso, la figura di prima proiettata nei due piani, quello rosso e quello nero, ossia quello perpendicolare all’orbita di Giove (sopra) e quello che contiene l’orbita di Giove (sotto). Possiamo anche dire che il primo fa vedere l’orbita della Terra (azzurra) di taglio e il secondo dall’alto (o dal basso, tanto è uguale…). Ancora più interessante è vedere la coppia Terra-Sole da Giove su un piano perpendicolare alla direzione Giove-Sole, come mostrato nel riquadro a destra. Beh… dovevamo aspettarcelo: la Terra descrive una specie di ellisse attorno al Sole che ha la distanza verticale superiore minore di quella inferiore (i famosi angoli differenti di cui abbiamo parlato prima), ma che si allontana verso destra e verso sinistra dello stesso valore (siamo ai nodi, ovviamente).  Questa danza attorno al Sole dura, ovviamente, un anno. L’importante è, però, che due volte all’anno la Terra si trova esattamente sullo stesso piano in cui il Sole gira attorno a Giove e questo fatto è molto importante. Come potete facilmente intuire, questo doppio attraversamento non dipende dall’inclinazione dell’orbita di Giove rispetto all’eclittica.

Purtroppo, questo punto è normalmente capito poco da chi cerca di spiegare in modo grossolano il fenomeno o fidandosi solo dei programmi “pappa pronta”. Mettiamoci pure nel caso più sfortunato possibile, ossia imponiamo che l’eclittica formi un angolo di 90° con il piano di Giove. Possiamo facilmente disegnare la configurazione in Fig. 27. Cosa cambia rispetto a prima. Sicuramente i due punti sopra e sotto l’orbita di Giove (T₁ e T₃) si vedono da Giove molto più distanti (prospetticamente) rispetto al Sole (se facessimo i calcoli troveremmo un valore di circa 13°), ma i punti T₂ e T₄ rimangono gli stessi, ossia continuano a coincidere con i due nodi.

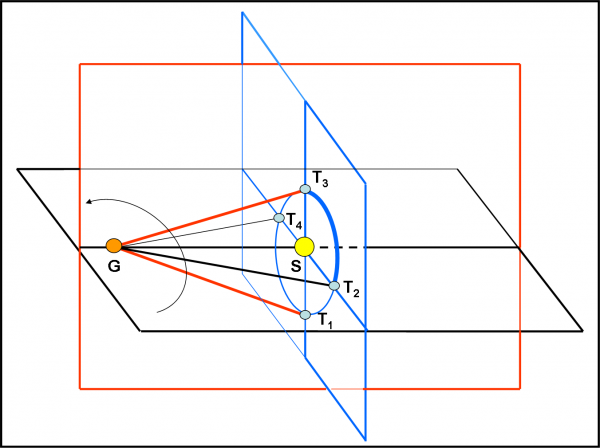
Tuttavia, è proprio ai nodi che la Terra si trova sul piano Giove-Sole e quindi in quei punti segue sicuramente le regole del Sole riguardo alla visibilità dei fenomeni tra satelliti: se il Sole vede i transiti, li deve vedere anche la Terra! Risulta chiaro che l’inclinazione dell’orbita del pianeta rispetto a quella terrestre conta ben poco ai fini della visibilità dei transiti “terrestri”. Il vero angolo fondamentale rimane sempre quello tra piano dell’orbita gioviana e piano equatoriale del pianeta gigante. Solo lui impone una visibilità dei transiti mutui (sia tra satelliti e Giove, sia tra i satelliti) più o meno continua (come abbiamo visto nei capitoli precedenti).

In ogni modo, ogni circa sei anni il Sole DEVE vedere il piano equatoriale di Giove esattamente di taglio (i nodi tra equatore e orbita). La terra segue il Sole nel suo moto, danzandogli attorno e ogni sei mesi si trova, come abbiamo visto poco fa, nel piano equatoriale di Giove. La conseguenza finale è abbastanza ovvia, ma la vedremo ancora meglio tra poco.

Adesso facciamo un passetto “professionale” in più e torniamo alla ben nota sfera celeste giovicentrica. La ridisegno ancora una volta (anche se ormai le diamo del “tu”…), aggiungendo solo un particolare decisamente interessante. In Fig.  28 vi è il solito cerchio massimo nero che rappresenta il percorso del Sole, che completa il suo giro in 11.86 anni. Le coordinate sono le solite declinazione e ascensione retta. L’unica differenza è che sappiamo ormai molto bene che abbastanza vicino al Sole deve sempre stare la Terra.  Come fatto precedentemente, immaginiamo che il Sole si fermi in  una certa posizione per almeno un anno. Cosa vedremo fare alla Terra se vista da Giove? Una piccola quasi-ellisse azzurra, proprio quella che abbiamo costruito poco fa.

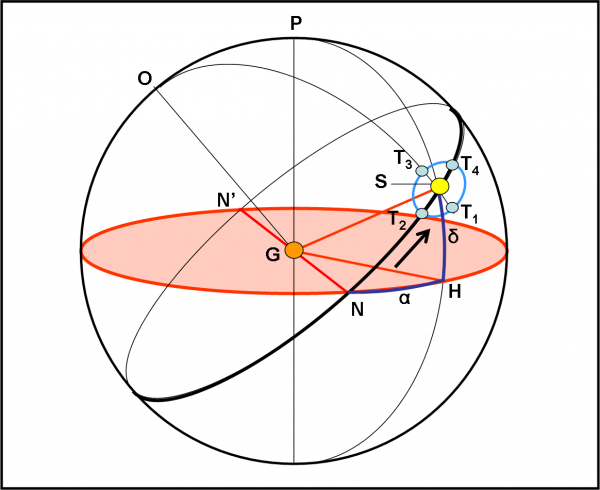
Attenzione: la possiamo costruire accuratamente e non solo qualitativamente. Infatti, gli angoli da cui Giove vede la Terra rispetto al Sole quando è nelle posizioni T₂ e T₄, li abbiamo già calcolati dai triangoli della Fig. 26. Basta disegnarli come archi lungo il cerchio massimo che passa per il Sole e per il polo O del suo piano orbitale, che è diretto, per definizione, perpendicolarmente al piano orbitale del Sole, ossia nel piano rosso della Fig. 25. Insomma, senza farla troppo lunga, è possibile calcolare perfettamente la quasi-ellisse che la Terra descrive attorno al Sole. Ovviamente, se la sappiamo descrivere nella sfera celeste giovicentrica, vuol dire che possiamo conoscere anche la declinazione e l’ascensione retta govicentriche di ogni suo punto.

Per riuscire a fare, matematicamente, questo piccolo “passo”, oltre che graficamente, è necessario applicare qualche semplice formula di trigonometria sferica. Per adesso, fidatevi di me, ma vi prometto che ci torneremo sopra e vedremo quanto è facile passare da un sistema di riferimento sferico ad un altro.

L’unico problema che abbiamo adesso dipende dal fatto che il Sole non ha nessuna voglia di stare fermo nel cielo, ma si muove costantemente, aumentando e diminuendo la sua declinazione rispetto all’equatore gioviano. Ebbene, non può certo spaventarci. Vuole dire che la Terra, oltre che descrivere la sua quasi-ellisse, si sposta di conserva con il Sole, descrivendo una specie di “sinusoide”, andando un po’ sopra e un po’ sotto alla traiettoria regolare della stella (questo fatto è veramente il punto fondamentale). A noi basta rappresentarla nella Fig. 29, in modo molto approssimato e qualitativo. Quanto basta, però, perché il solito “stupido” computer possa disegnare una traiettoria accuratissima: tutti i dati necessari glieli abbiamo già dati!

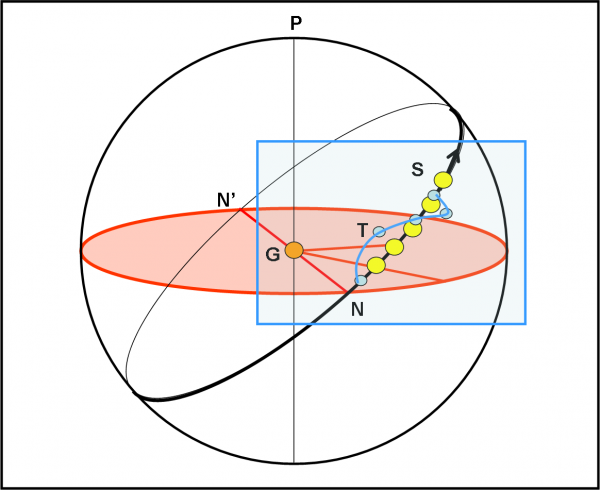
Che bello! Un’onda continua, a volte più ripida e a volte meno. D’altra parte pensate che per sei mesi la Terra viaggia nella stessa direzione del Sole, mentre per altri sei mesi si muove in direzione opposta. E’ ovvio che il risultato sia abbastanza “caotico”.

Prima di proseguire, immaginatevi questo movimento visto da Giove e mettetevi nei panni degli antichi scrutatori del Cielo. Se la situazione è così complicata quando si guarda da Giove, lo è anche quando si guarda dalla Terra e, quindi, non appare tanto strana l’introduzione degli epicicli per spiegare il moto planetario. Analogamente, potete rendervi conto della genialità di chi è riuscito, a spiegare tutto mettendo il Sole al centro e addirittura a scrivere le leggi orbitali. Non parliamo poi di chi ha capito che era tutto legato a una legge universale! Va beh… torniamo a noi.

Nella Fig. 29 ho disegnato un riquadro azzurro e lo riporto ingrandito nella Fig. 30, dove per diversi punti ho evidenziato le declinazioni e le ascensioni rette del Sole e della Terra. Inoltre, ho anche accoppiato le posizioni assunte dal Sole e della Terra nello stesso istante t. In tale modo, oltre alle coordinate giovicentriche, riusciamo anche a rappresentare il tempo che scorre. Non confondiamo, infatti, il tempo con l’ascensione retta. In un certo istante, Terra e Sole possono assumere, ovviamente, posizioni diverse. Analizziamole più attentamente, partendo dal basso a sinistra.

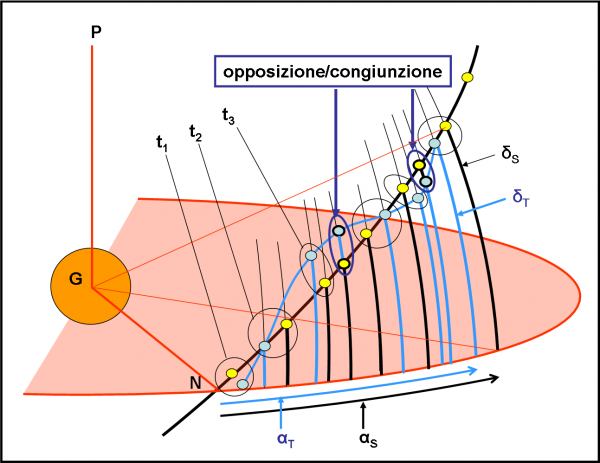
La prima coppia rappresenta il Sole la Terra poco dopo che il Sole è passato dal nodo ascendente N. Fortunatamente (state bene attenti a quello che dico!), la quasi ellisse del Sole è molto piccola e quindi la Terra deve sempre essere molto vicina al Sole, anche nel momento in cui lui è passato al nodo. Questo fatto implica che se i transiti sono visti dal Sole, lo sono anche dalla Terra. Il ogni modo, il Sole rimane abbastanza a lungo vicino al nodo, a sufficienza perché la Terra, anche con un’orbita più inclinata (ossia con una quasi-ellisse molto più allungata verso l’alto e verso il basso), riesca a passare nel suo moto attorno al Sole da declinazioni negative a positive e/o viceversa. Questo è il punto fondamentale! Passare da declinazioni negative a positive vuole dire attraversare l’equatore di Giove, ossia il piano dei satelliti e, quindi, vedere i loro piani orbitali di taglio (o quasi)!

In altre parole: condizione essenziale perché la Terra possa vedere i transiti dei satelliti su Giove (e tra di loro) è che la sua traiettoria apparente vista da Giove tagli il suo piano equatoriale. Dato che il Sole lo fa almeno una volta ogni sei anni e che la Terra gli gira attorno ne segue che anche il nostro pianeta è obbligato a farlo. Queste sono le uniche condizioni che permettono i transiti mutui tra satelliti! Pensateci bene e vi apparirà una conclusione di un’ovvietà quasi ridicola: altro che essere un problema per soli professionisti.

L’inclinazione piccola dell’orbita gioviana, rispetto a quella terrestre, implica soltanto che i transiti visti dal Sole e quelli visti dalla Terra capitino praticamente nello stesso periodo di tempo. Se l’orbita terrestre fosse più inclinata e/o descritta in un  periodo più lungo di un anno, i transiti solari e quelli terrestri potrebbero avvenire in tempi anche abbastanza diversi. Provate a pensarci sopra e vedrete che la faccenda è molto semplice. Vi do un aiuto. Se il periodo fosse più lungo, la sinusoide della figura precedente si allungherebbe e quando il Sole si trova al nodo N (o lì vicino), la Terra potrebbe trovarsi molto distante da quel punto e quindi non vedere i transiti. Idem, se si spostasse troppo verso l’alto o verso il basso. Tuttavia, lo ripeto ancora una volta, prima o poi la Terra sarebbe comunque obbligata ad attraversare l’equatore di Giove e assisterebbe tranquillamente ai transiti mutui dei satelliti. Tutta questa attenzione riguarda solo i transiti mutui tra i satelliti e non i transiti dei satelliti sul disco di Giove. In questo secondo caso i paralleli di visibilità sono molto più “permissivi” e permettono di allontanarsi molto di più dai nodi dell’equatore di Giove.

Potevamo risolvere la questione in modo ancora più sbrigativo, senza tante parole. Bastava che nella Fig. 29 avessimo disegnato i paralleli azzurri che limitano la visibilità dei transiti su Giove e tra satellite e satellite, ossia riportarci alle figure adottate negli articoli precedenti. E’ proprio quello che facciamo adesso. Anzi, andiamo oltre e consideriamo il diagramma che descrive la declinazione giovicentrica del Sole in funzione del tempo, aggiungendo alla declinazione del Sole anche quella della Terra, con la sua strana curva che continua a danzare attorno a quella regolare del Sole.

Lo rappresentiamo nella Fig. 31, dove abbiamo inserito sia la fascia azzurra (relativa alla visibilità di transito di tutti i satelliti su Giove) sia quella verde (relativa alla visibilità di almeno un transito mutuo tra i satelliti). Insomma, abbiamo ripetuto la Fig. 22,  aggiungendovi la traiettoria giovicentrica della Terra. Un gioco veramente da ragazzi che ci permette di stabilire subito quando e come si verificano sia i transiti rispetto al Sole “acceso” (eclissi se visti dalla Terra) sia rispetto alla stessa Terra (osservatore passivo).

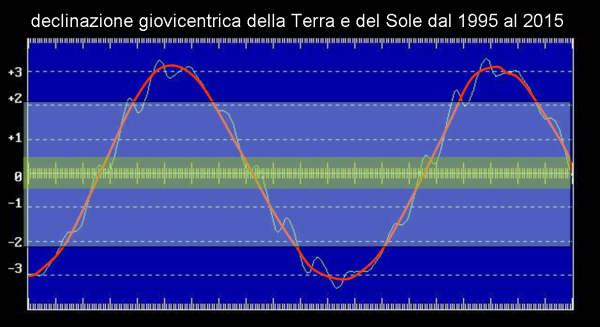
Torniamo ancora un attimo alla Fig. 30. Nella traiettoria Sole-Terra vi sono altri punti particolari. Li ho indicati come congiunzioni/opposizioni. Essi sono gli istanti  in cui l’ascensione retta del Sole e della Terra sono uguali. Ciò può essere possibile in due casi, che avevo già descritto nell’articolo sulle opposizioni… L’opposizione si ha quando il Sole e Giove si trovano a 180° l’uno dall’altro, La congiunzioni quando Sole e Giove sono entrambi nella stessa direzione. Viste da Giove entrambe le configurazioni danno, ovviamente, la stessa ascensione retta sia per la Terra che per il Sole. La situazione, molto schematizzata e vista dall’alto (non considerando, quindi, l’inclinazione orbitale) è riportata in Fig. 32. E’ facile intuire che per le osservazioni sono molto più convenienti le opposizioni, dato che Giove si vede di … notte.

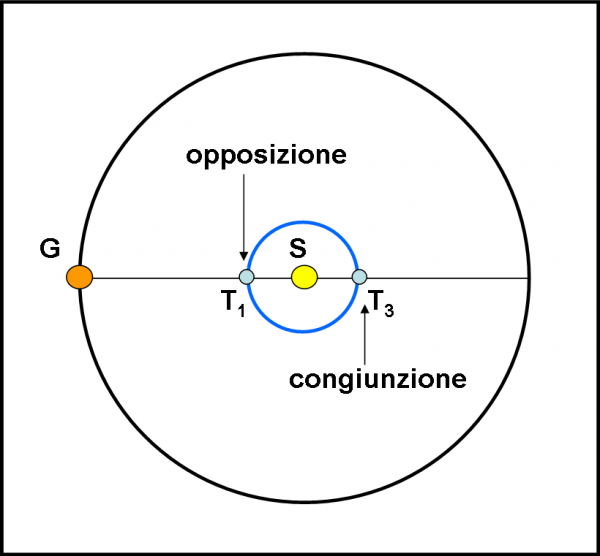
Siamo proprio arrivati alla fine. Possiamo concludere con la figura più tecnica che nasce spontaneamente dal nostro lento avvicinamento. La Fig. 33 riporta il periodo dei transiti e delle eclissi mutue tra satelliti gioviani nel periodo 2003-2004. La zona verde è quella che già conosciamo bene ed è relativa alla visione di almeno il transito mutuo tra Io ed Europa. Come vedete per un certo numero di mesi sono visibili sia i transiti mutui tra satelliti (curva sinusoidale della Terra) sia le eclissi mutue (curva regolare del Sole).

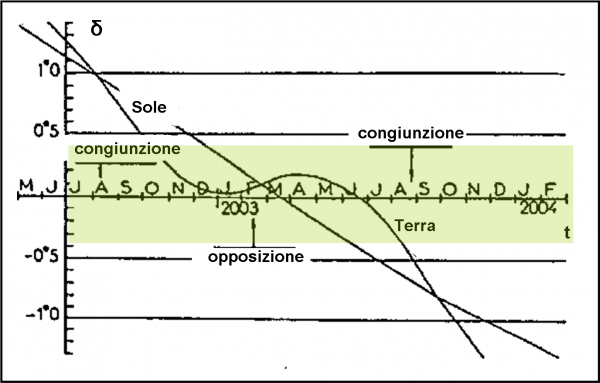
Siamo riusciti, con carta e matita, a ricostruire un po’ alla volta il diagramma professionale che illustra le condizioni ideali per osservare, con gli strumenti più adatti (normalmente i fotometri fotoelettrici come fa Kepler), i fenomeni mutui tra i satelliti di Giove. Un diagramma è comunque sempre e solo un diagramma. Per pianificare le osservazioni bisogna riferirsi alle tabelle che danno con grande precisione gli istante di inizio e fine dei vari fenomeni. A produrre queste tabelle ci pensano, ovviamente, i soliti “schiavi” elettronici.

A questo punto, si può anche utilizzare Celestia & co., per vedere sullo schermo la stessa cosa che noi siamo riusciti a disegnare da soli. Si può anche fare… ma non penso che possa più dare alcuna soddisfazione. Chi è interessato veramente a osservare gli eventi deve, comunque, riferirsi alle tabelle. Chi, invece, è interessato al come e perché, trova tutte le risposte solo attraverso il ragionamento e non certo con una “pappa pronta” che spiega poco o niente. Insomma, celestia e i suoi fratelli, o eventuali migliorie personalizzate, non servono a nessuno, né agli osservatori né agli amanti delle regole del Cosmo!

Concludo con una constatazione e un invito per chi avesse tempo e voglia. La trattazione che abbiamo seguito non vale certamente solo per Giove, ma per qualsiasi sistema satellitario. Basta cambiare i parametri orbitali e si ottengono TUTTE le figure ricavate per Giove. Anzi, vi dirò di più: i casi di Saturno e dei pianeti esterni (possiamo anche considerare l’ex Plutone) sono decisamente più favorevoli, dato che l’orbita della Terra, vista da loro, diventa ancora più stretta e gli angoli di vista diminuiscono. Inoltre, abbiamo il caso molto interessante di Urano. Il suo piano equatoriale forma un angolo di circa 90° con il piano orbitale. Qualche problema?  Nessuna paura: il Super Kepler Sole sa benissimo che anche in questo caso peculiare ci sono sempre e comunque due punti sempre sicuri, ossia i nodi… Divertitevi se volete…

Ancora una cosa… Non pensate che tutto questo lungo articolo sia servito solo ai satelliti dei pianeti e ai loro fenomeni mutui. E’ servito a introdurre le coordinate sferiche e a spostarle da un oggetto a un altro, cambiando piano di riferimento.  Potrebbe essere arrivato il momento di spiegare nel modo giusto e con le dovuta accuratezza i vari sistemi di coordinate e la matematica che permette di eseguire le trasformazioni. L’astronomia ha assoluto bisogno della trigonometria sferica e ormai siete in grado di affrontarla (sempre che non la conosciate già). Se siete d’accordo lo faremo quanto prima. Ancora una volta vedrete che le vere difficoltà sono tutta un’altra cosa. Quindi, vi prego di digerire bene questo articolo che , vi assicuro, non è assolutamente noioso e/o inutile. Mi fido di voi…

 

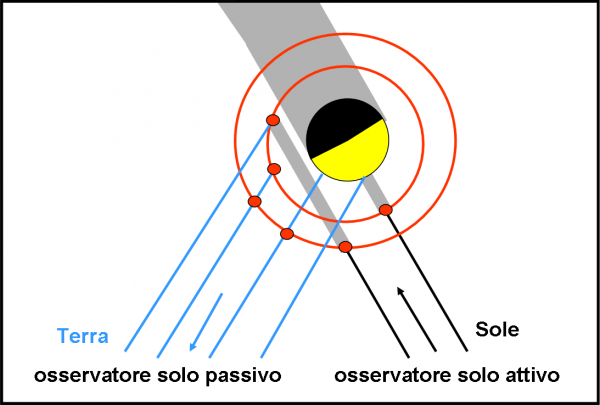
QUI una splendida doppia eclissi mutua, "catturata" con mezzi a dir poco elementari da un astrofilo giapponese il 17/1/2015

Dove dovrebbe essere posizionato un Kepler alieno per avere una certa probabilità di scoprire il pianeta Terra attraverso il metodo dei transiti? leggete QUI e lo scoprirete!

QUI tutti gli articoli sul telescopio spaziale Kepler, che ha scoperto migliaia di esopianeti (e molto altro...) grazie al metodo dei transiti

Questo articolo è stato inserito nelle sezioni d'archivio "Sistema Solare", "Astronomia classica" e "Giove e i suoi tesori"