Cari amici, non sono molto contento dei risultati (lo dico perché siamo tra AMICI, ovviamente). Innanzitutto, perché solo pochissimi hanno risposto. Ma soprattutto non mi è piaciuto il modo come hanno risposto. Perché? Quasi tutti non hanno seguito il semplice procedimento che avevo illustrato nel capitolo 24, ma hanno liberamente utilizzato concetti e procedimenti che ancora non avevo spiegato. Tutto ciò può dimostrare che loro sono bravi e preparati, ma ha creato molta confusione nei meno preparati. Probabilmente aiutandoli a lasciar perdere un argomento che si stava complicando in modo non gestibile attraverso le lezioni già pubblicate. Insomma, siamo caduti nel solito errore che fa odiare la matematica: la perdita di un ordine semplice, chiaro e umile. Il succo delle 24 lezioni non è, invece, questo e nemmeno quello di fare classifiche di bravura, ma solo quello di tentare di fare amare una materia fondamentale per capire l’Universo.

Prima di darvi le soluzioni, fatemi fare un bel “rimbrotto” (amichevole) a coloro che mi hanno risposto. Hanno chiaramente dimostrato (non ho nemmeno voluto controllare i risultati, ma penso siano tutti giusti) che hanno già studiato le funzioni. Tuttavia, non hanno seguito quasi mai il semplice procedimento che avevo illustrato nel capitolo 24. Non solo, però. Hanno già parlato di derivata seconda e cose del genere. In poche parole, hanno dimostrato di conoscere la materia, ma hanno creato molta confusione in chi l’affronta per la prima volta. Insomma, non mi hanno aiutato! Da un altro lato, però, hanno dimostrato un punto importante: se la matematica viene spiegata saltando molti passaggi giudicati ovvi e si applicano concetti non ancora spiegati in dettaglio si ottiene proprio quello che capita in molte scuole, ossia si odia la matematica!

Ovviamente, sto scherzando, ma stiamo attenti, sia voi che io, a non presentare la matematica e i suoi risultati in modo troppo approssimativo, senza le dovute spiegazioni e senza tanta umiltà. Prima di dare tutti i  risultati, aspetto ancora un po’ per vedere se questa trattazione estremamente umile può incitare i meno esperti a cimentarsi con le altre funzioni…

Soluzione del primo esercizio

y = 2x² - x

Punti all’infinito

Basta far tendere x a + e - ∞ e vedere cosa succede alla y. Ovviamente dobbiamo usare il “limite”…

lim _{x→ + ∞} y = lim _{x→ + ∞} (2x² - x) = ∞ - ∞

sembrerebbe una forma indeterminata… ma noi sappiamo benissimo come non farci prendere in giro dalle apparenze. Da un lato, potremmo dire che x² è di ordine superiore rispetto a x e quindi il risultato è + ∞, dato che basta fare il limite del monomio con il grado più alto. Dall’altro, potremmo anche mettere in evidenza la x e poi passare al limite, ossia:

lim _{x→ + ∞} (2x² - x) = lim _{x→ + ∞} x(2x –-1) = lim _{x→ + ∞} x ･ lim _{x→ + ∞} (2x - 1) = ∞ ･∞ = + ∞

Ricordando ovviamente la regola del limite di un prodotto e il fatto che il limite di una costante  è sempre la costante. Ovviamente, aggiungere o togliere un numero a  ∞, lo fa restare ∞.

Insomma, il risultato è elementare, ma per i meno esperti sarebbe bene andare a rivedersi le operazioni sui limiti…

Analogamente:

lim _{x→ - ∞} y = lim _{x→ - ∞} (2x² – x) = lim _{x→ -∞} x ･ lim _{x→ - ∞} (2x -1) = - ∞ ･ - ∞ = + ∞

Anche per x che tende - ∞ la y tende a + ∞. Era ovvio aspettarselo dato che il termine di grado maggiore è un quadrato e quindi il quadrato di qualsiasi numero è sempre un numero positivo.

La nostra funzione va a + ∞  sia a sinistra che a destra. Questo primo risultato lo vediamo nello schema dei Fig. 1, dove inseriamo due freccette che indicano questo risultato.

Intersezioni con gli assi

Iniziamo dalle intersezioni con l’asse delle y. Per trovarle, basta imporre x = 0. Abbiamo:

y = 2x² – x = 0 – 0 = 0

La curva passa per l’origine degli assi O(0,0), dato che quando x = 0 anche y = 0.

Troviamo, adesso, le intersezioni con l’asse delle x. Per far questo dobbiamo porre y = 0. Otteniamo:

0 = 2x² – x

Scriviamola meglio:

2x² – x = 0

E’un’equazione di secondo grado in x, ma risolvibile facilmente dato che non vi è il termine noto. E’ sufficiente mettere in evidenza x e si ha:

x(2x – 1) = 0

Affinché questa prodotto sia ZERO è necessario che almeno uno dei due fattori sia ZERO. Ossia:

x = 0

oppure

2x – 1 = 0

La soluzione con x = 0, l’abbiamo già trovata ed è quella relativa all’origine. Rimane un’altra soluzione data dalla seconda equazione di primo grado in x. Otteniamo:

2x – 1 = 0 -> 2x = 1 -> x = ½ = 0.5

La funzione taglia l’asse delle x anche nel punto P(0.5,0).

Riassumendo, la curva passa per l’origine e poi tocca nuovamente l’asse delle x (y = 0) dove l’ascissa vale 0.5. Anche questo risultato lo inseriamo nella Fig. 1.

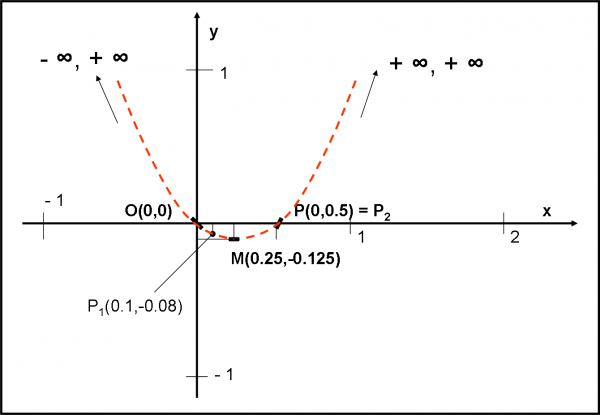
Punti di massimo, minimo o flesso orizzontale

Per vedere se esistono questi punti dobbiamo effettuare la derivata di y e poi trovare per quale valore di x va a zero. Infatti, sappiamo che i massimi, i minimi e i flessi orizzontali hanno la derivata uguale a zero, ossia la tangente alla curva in quel punto è una retta ORIZZONTALE.

y’ = d(2x²-x)/dx = 2d(x²)/dx- d(x)/dx = 4x – 1

Abbiamo utilizzato alcune delle proprietà delle derivate (andate a rileggervele…).

Poniamo la derivata uguale a zero

4x – 1 = 0 -> 4x = 1 -> x = 1/4 = 0.25

Non ci resta che vedere quanto vale la y per x = ¼

y = 2(1/4)² - ¼  = 2/16 – ¼ = (2 - 4) /16 = - 2/16 = - 1/8 = - 0.125

Il punto in cui la derivata si annulla è M (0.25, - 0.125)

Dobbiamo solo scoprire se è un massimo, un minimo o un flesso orizzontale.

Scegliamo un punto alla sinistra e uno alla destra di M e vediamo se la sua y è maggiore o minore di quella del punto a derivata nulla. Scegliamo x₁ = 0.1 e x₂ = 0.5 (ad esempio). Ricaviamo i relativi valori della y:

y₁ = 2(0.1)² – 0.1

e

y₂ = 2(0.5)² – 0.5

Ossia:

y₁ = - 0.08

y₂ = 0

Avete notato che ho scelto come punto a destra del punto a derivata nulla, proprio quello in cui sapevo già che la curva toccava l’asse delle x. Potevo sceglierne un altro, ma in tal modo abbiamo verificato un risultato già ottenuto (non fa mai male).

Confrontiamo adesso y₁ e y₂ con la y_M del punto a derivata nulla. y_M valeva - 0.125.

y₁ > y_M  dato che - 0.08 > - 0.125

y₂ > y_M  dato che 0 > - 0.125

Sono entrambe maggiori della y_M (punto a derivata nulla) e quindi siamo nel caso di MINIMO. Il punto M (0.25, -0.125) è un minimo della nostra funzione. Per come l’abbiamo trovato è anche l’unico punto particolare di questo tipo.

Ovviamente, i punti che ci sono serviti per controllare che tipo di punto particolare è M, sono punti della curva e ci servono per abbozzarne una rappresentazione.

Anche questo procedimento lo riportiamo in Fig. 1.

Conclusioni

La nostra funzione ha un numero sufficiente di informazioni per essere tracciata in modo molto preliminare. Da sinistra a destra: deve partire da più infinito, toccare l’origine, scendere fino a M, risalire toccando P e andare nuovamente a più infinito. Cosa dovremmo farla per migliorarla? Trovare molti altri punti che le appartengono, ossia fare una tabellina con vari valori di x e ricavare le corrispondenti y e poi tracciare la curva che passa per tutti questi punti.

Il caso che abbiamo studiato è ovviamente un caso estremamente semplice e la curva finale poteva capirsi fin dall’inizio, dato che la y è rappresentata da un polinomio di secondo grado in x e quindi deve essere per forza una conica. In particolare, risulta una parabola e quindi ha una simmetria tra ramo discendente e ascendente. Insomma, vi sono vari modi per saperla descrivere in modo analitico.

Tuttavia, non sempre la funzione è una curva conosciuta e il procedimento “rozzo” e preliminare che abbiamo eseguito è il procedimento migliore per cominciare ad avere un’idea di cosa dobbiamo studiare. Questo è solo il primo passo, ma -come avete visto- è stato sufficiente a dare uno schema di massima delle caratteristiche essenziali della funzione.

A tutti coloro che stanno affrontando questa problematica per la prima volta, consiglio vivamente di seguire questo procedimento solo apparentemente lungo, monotono e -spesso- quasi banale. Solo così si sarà in grado di affrontare funzioni ben più complesse e molto meno conosciute “a priori”.

Aspetto ancora un po’ a dare gli altri risultati, sperando di invogliare i meno esperti a provarci. seguendo quanto ho fatto io per il primo esercizio…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica