Categorie: Corpi minori
Tags: asse di rotazione curva di luce forma fotometria polo
Scritto da: Vincenzo Zappalà
Commenti:8
Datemi un punto luminoso e vi svelerò un mondo ***
Questo articolo è stato inserito nella serie "I miei amici asteroidi", nella quale sono raggruppati gli articoli più significativi in materia.
Approfitto della “pausa” per richiamare questo articolo che racconta una parte importante degli inizi della mia vita professionale. Niente di speciale, ma penso sia apprezzato da chi ama la geometria.
Come si ottiene il periodo di rotazione, attorno al proprio asse, di un asteroide? E’ semplicissimo rispondere. Basta misurare il flusso di luce che riceviamo e costruire la relativa curva di luce in funzione del tempo. Dato che gli asteroidi emettono solo luce riflessa e sono corpi di forma irregolare, la quantità di luce che inviano verso terra dipende soltanto dalla superficie apparente che mostrano all’osservatore. Durante la rotazione completa questa cambia continuamente, passando da un massimo di luce (area massima) a un minimo (area minima) e poi ancora a un massimo e a un altro minimo (Fig. 1).
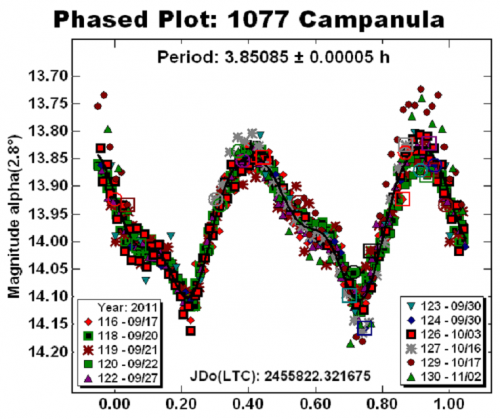
Questa doppia onda è tipica delle forme irregolari. Se avessimo una sfera mezza chiara e mezza scura avremmo, invece, solo un massimo e un minimo di luce (come, ad esempio, capita per Vesta).
Le osservazioni fotometriche permettono di stabilire in una sola notte, o, più frequentemente in una serie di notti, la curva di luce completa dell’oggetto celeste. Il periodo di rotazione è la durata di tempo che intercorre tra un massimo (o minimo) e la sua successiva apparizione. Normalmente, quasi tutti gli asteroidi sono di forma irregolare e quindi le loro curve di luce complete sono caratterizzate da due massimi e da due minimi per periodo.
Se ci pensate bene, già questo risultato è ammirevole: l’analisi della luce inviataci da un punto che appare tale anche con i maggiori telescopi, permette di conoscere un’entità fisica come il periodo di rotazione. Non è stata conquista da poco e io sono estremamente contento e onorato di aver fatto parte del limitato numero di “pionieri” di questa “semplice” tecnica osservativa applicata ai piccoli corpi del sistema solare (anni ’70). Oggi, è alla portata di tutti, ma continua a regalare dati di estrema importanza per lo studio dell’evoluzione fisica della fascia asteroidale.
Queste cose, però, le sapete già. Tuttavia, lo studio della curva di luce va ben oltre. Può, sotto certe ipotesi non eccessivamente restrittive, permettere la ricostruzione della forma “generale” del corpo celeste e la direzione del suo asse di rotazione. Parametri, tra l’altro, molto importanti per lo studio dell’evoluzione del momento angolare e della forma dei frammenti di un corpo andato catastroficamente distrutto. Vi prego di ricordare che proprio la forma di alcuni asteroidi medio-grandi ci aveva permesso di individuare gli ellissoidi a tre assi e la struttura ad “ammasso di pietre”, oggi universalmente riconosciuta (qui).
Mentre la determinazione del periodo di rotazione è normalmente cosa rapida e facile (una volta bastava un buon fotometro fotoelettrico, oggi un buon CCD), più complicata è la determinazione della forma e dell’asse di rotazione. In questo articolo voglio raccontarvi uno dei vari metodi, quello che ho usato più spesso (in quanto messo a punto proprio da… me) e che risulta anche il più semplice da spiegare geometricamente e senza utilizzare formule più o meno complicate.
L’ipotesi fondamentale che bisogna fare per poter arrivare a un risultato accettabile è che la forma dell’asteroide sia assimilabile a un ellissoide a tre assi (a>b>c), rotante attorno al semiasse minore c. Attenzione! Questo non vuol dire che tutti gli asteroidi siano forme di equilibrio, ma solo che, come tutti i frammenti collisionali, hanno forme più o meno allungate e non simmetriche (molti sono a forma di nocciolina americana, come questo). La rotazione intorno all’asse minore è comprovata dalla teoria e dalla casistica, e si lega a condizioni che si riferiscono al momento angolare.
Le forme a tre assi sono più che giustificabili, guardando i sassi di una spiaggia ciottolosa in cui il mare abbia smussato gli angoli delle pietre (Fig. 2).

Ammettiamo, quindi, che il nostro asteroide si presenti come un ellissoide a tre assi, rotante attorno all’asse minore. Magnifico. Tuttavia, noi continuiamo a vedere, da terra, solo un punto luminoso e quindi l’ellissoide può essere orientato in qualsiasi modo nella sua posizione celeste.
La sua prima curva di luce, in genere, ci aiuta già a capire la forma grossolana: se l’ampiezza, ossia la differenza tra massimi e minimi, è abbastanza rilevante vuol dire che l’ellissoide è piuttosto allungato. Come mai? Presto detto. Prendiamo ad esempio un oggetto che abbia l’asse di rotazione perfettamente perpendicolare alla linea di vista. In Fig. 3, nella parte alta, vi è l’ellissoide visto dal polo (e quindi l’ellisse mostra proprio gli assi maggiori a e b), mentre le due rappresentazioni sottostanti si riferiscono a vari istanti.
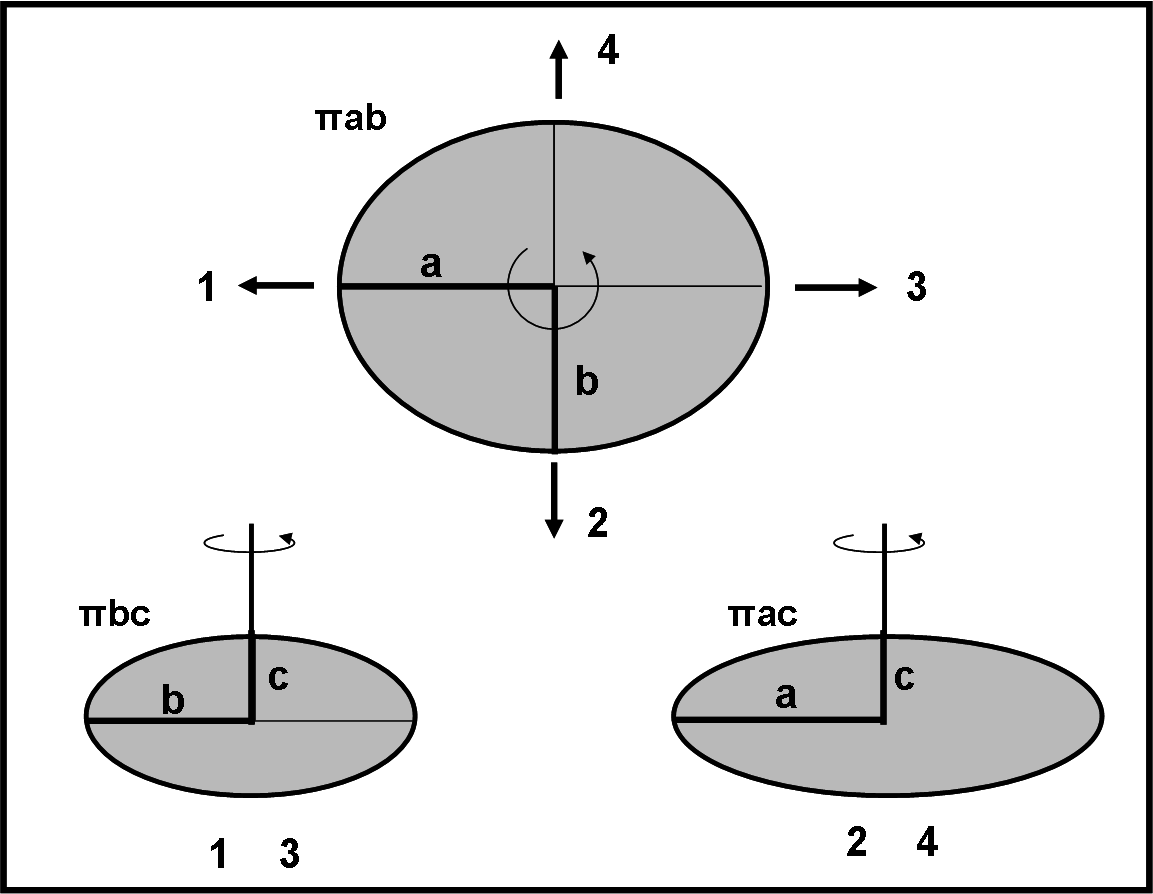
In particolare, l’area della superficie ellittica vista da terra passa da un minimo (1) quando si vede l’asse intermedio b (πbc) a un massimo (2) (dopo novanta gradi di rotazione) quando si vede l’asse maggiore a (πac). Poi, dopo altri 90°, di nuovo πbc (3), seguita da πac (4), per concludersi, infine, nuovamente con πbc (1). L’asse minore c si vede sempre, proprio perché l’asse di rotazione è perpendicolare alla linea di vista.
In questo caso così favorevole si potrebbe immediatamente risalire al rapporto tra gli assi maggiori dell’ellissoide (a/b), scrivendo la formula (ormai ben conosciuta da tutti):
m2 – m1 = – 2.5 log (Imax/Imin) = – 2.5 log (Amax/Amin) = – 2.5 log (πac/ πbc) = – 2.5 log (a/b)
notando che m2 – m1 è proprio l’ampiezza della curva di luce in quanto è la differenza di magnitudine tra massimo e minimo, mentre l’intensità luminosa che entra nel logaritmo è, nel caso di luce riflessa, proporzionale solo all’area apparente vista dall’osservatore. In altre parole, più uno “specchio” è grande e più luce riflette.
Se fossimo sicuri di essere nelle condizioni della Fig. 3 avremmo già ottenuto un risultato importante. Purtroppo, esso è solo un caso fortunato, che, però, si verifica sempre (prima o poi) per qualsiasi asteroide e per qualsiasi orientazione del suo asse di rotazione. Basta avere pazienza. Ora vi mostro perché…
Consideriamo due casi estremamente particolari, ma molto indicativi. L’asteroide si trova su un’orbita circolare e complanare con quella terrestre. La direzione del suo asse di rotazione è perpendicolare all’orbita stessa (Fig. 4).
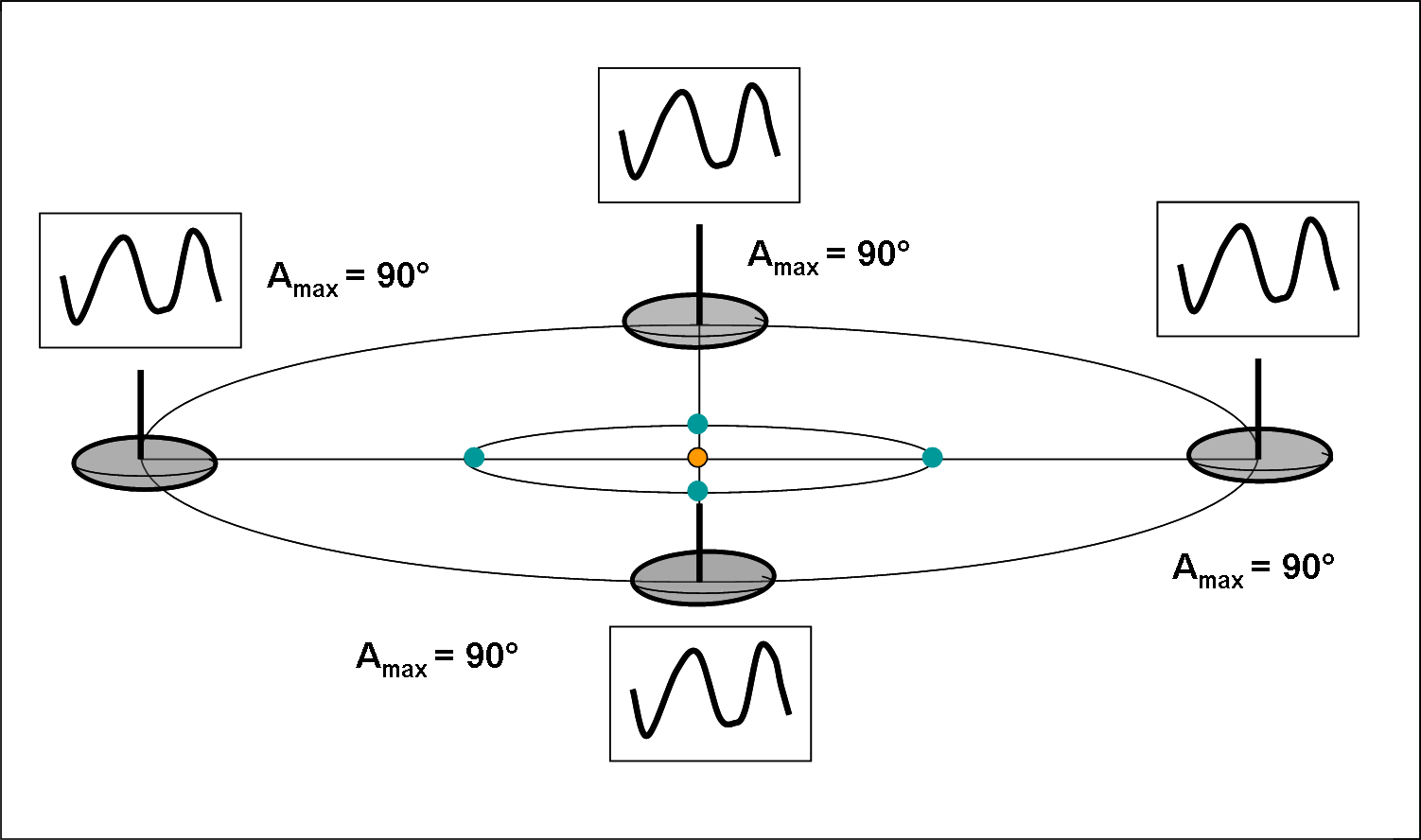
Le mutue posizioni Terra-asteroide sono mostrate per 4 particolari opposizioni. In realtà, sarebbe stato inutile, in quanto l’angolo tra asse di rotazione e linea di vista rimane sempre uguale a 90° (visione equatoriale). In qualsiasi opposizione si osservi, si ricade nel caso di Fig. 3 (in basso). Otteniamo sempre la stessa ampiezza di curva di luce.
Già dalla prima curva di luce, si ricava subito il rapporto tra gli assi maggiori a/b, ma nessuna informazione sul rapporto a/c o b/c. Sappiamo anche la direzione dell’asse di rotazione (non variando l’ampiezza nelle varie opposizioni l’asse deve essere perpendicolare). Se facciamo un diagramma dove in ascissa mettiamo, ad esempio, la longitudine dell’asteroide e in ordinata l’ampiezza della curva di luce, otteniamo dei punti perfettamente allineati lungo una parallela all’asse delle ascisse.
Altrettanto peculiare, ma più interessante, il caso mostrato nella Fig. 5.
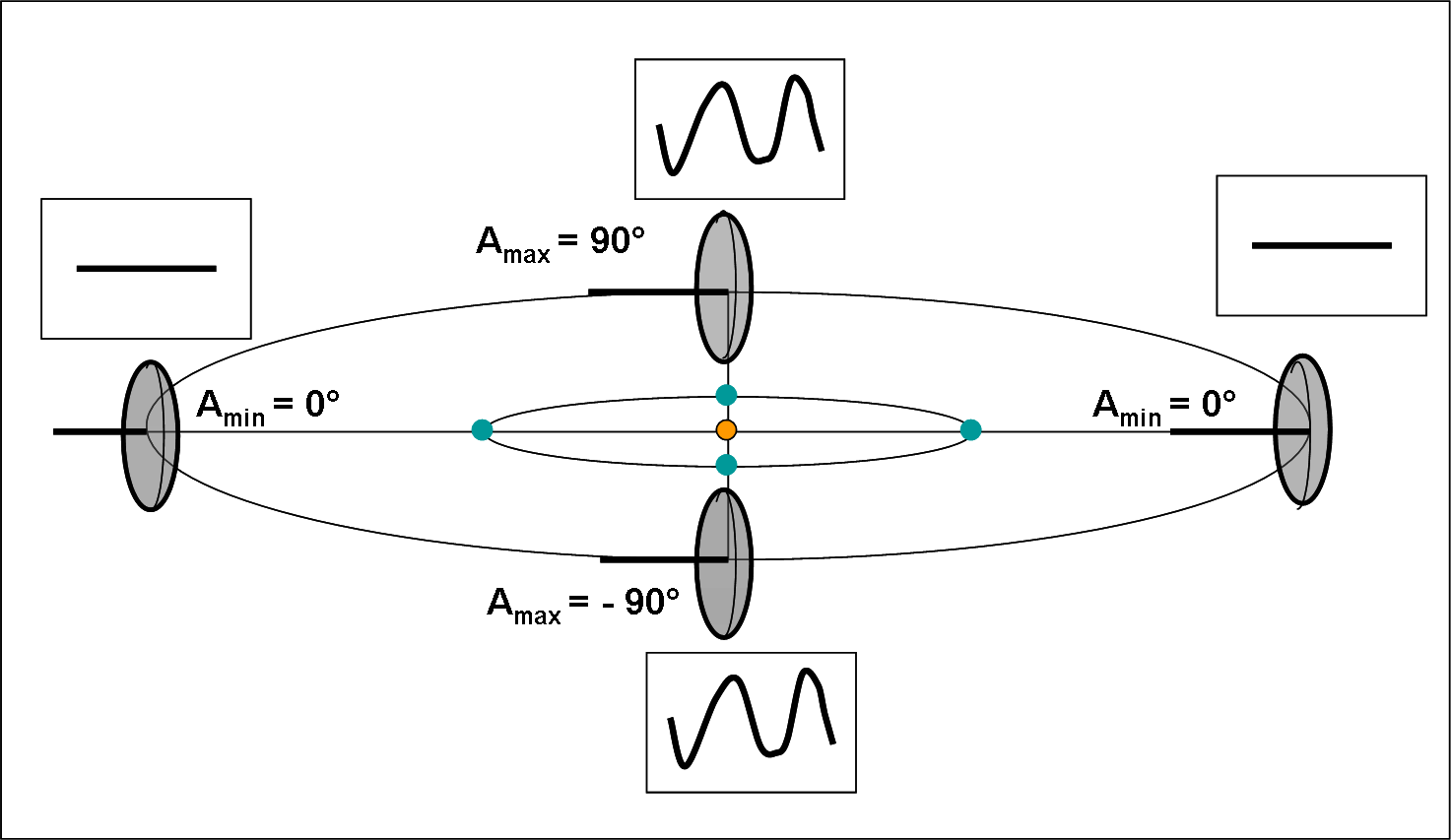
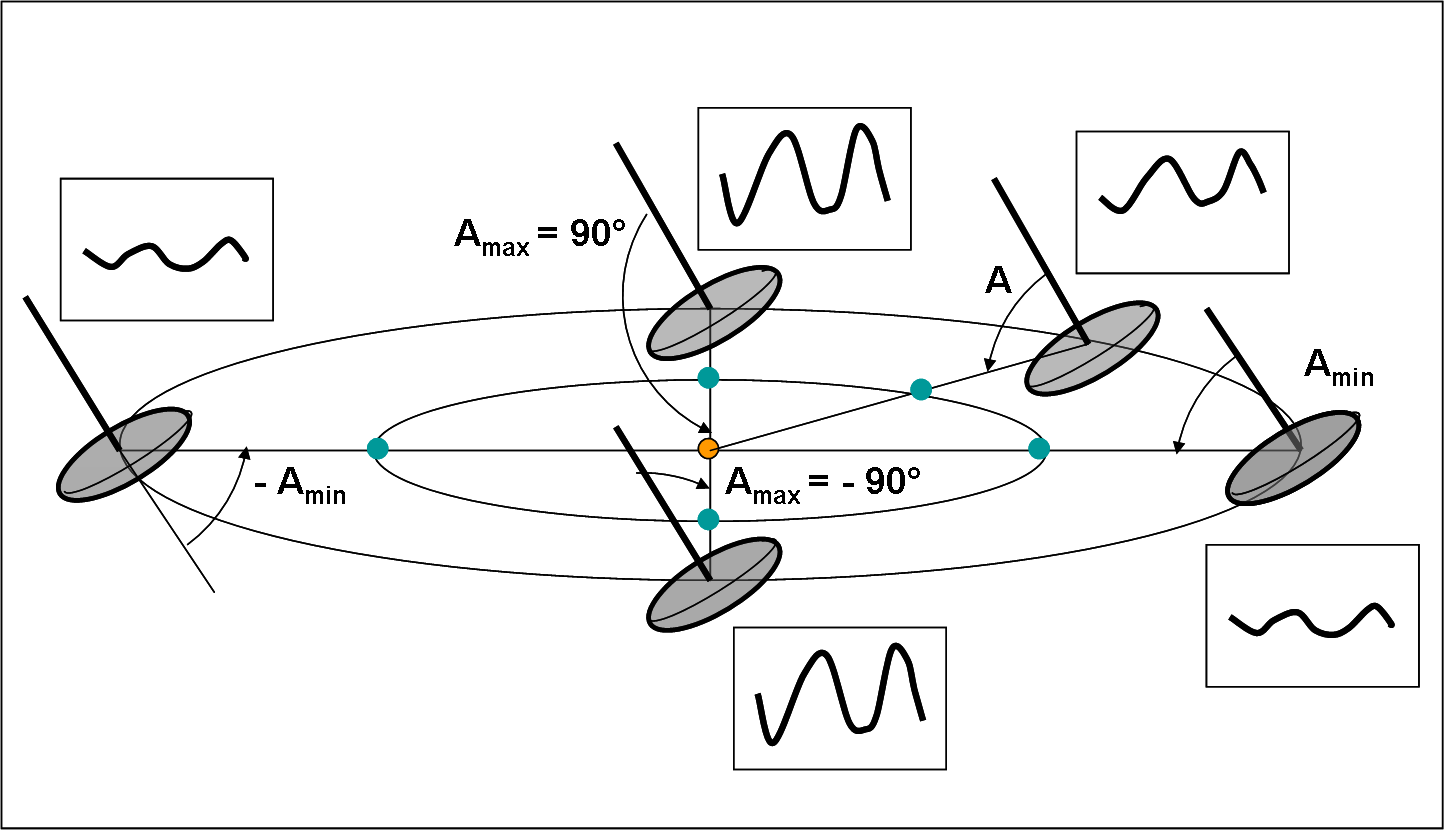
In questo caso le orbite sono sempre complanari, ma l’asse di rotazione giace sul piano orbitale (un po’ come Urano). Vi è allora un punto in cui la Terra vede l’asteroide proprio lungo l’asse di rotazione (posizione a destra), ossia l’osservatore non rileva nessuna variazione luminosa durante il periodo di rotazione dell’oggetto celeste (visione polare). Siamo, infatti, nel caso mostrato in alto nella Fig. 3. Per un opposizione che cada a 90° da questa si ha, invece, un angolo tra asse di rotazione e linea di vista uguale a 90° (come in Fig. 3, in basso) e quindi l’ampiezza della curva raggiunge il suo valore massimo (visione equatoriale). Dopo altri 90° ricadiamo nella visione polare (anche se si vede il polo opposto) e poi ancora nella visione equatoriale.
Nelle configurazioni intermedie tra questi quattro casi peculiari, l’asse di rotazione dell’asteroide forma un angolo variabile tra 0° e 90°, che prende il nome di angolo di aspetto A. In realtà l’angolo andrebbe da 0° a 180° o da – 90° a + 90°, a seconda di come si misuri. Questo fatto ha poca importanza (per adesso, ma ne parleremo più avanti), dato che abbiamo assunto come forma dell’asteroide quella di un ellissoide perfetto, la cui luminosità dipende solo dall’area apparente mostrata all’osservatore.
Al variare dell’angolo di aspetto, l’ampiezza assume valori intermedi tra il valore minimo, uguale a zero (visione polare), e il valore massimo (visione equatoriale). Osservazioni eseguite in varie opposizioni permettono di costruire la curva ampiezza-longitudine. Questa volta non è più una retta parallela all’asse delle ascisse, ma una curva continua che assomiglia, in qualche modo, a una curva di luce. Il valore massimo è sicuramente la visione equatoriale e quindi ci permette di conoscere nuovamente a/b. Inoltre, la posizione in cui l’ampiezza diventa zero, indica proprio la longitudine del polo.
In questo caso peculiare, sappiamo anche che la latitudine della direzione dell’asse di rotazione è zero, dato che l’ampiezza minima è nulla e quindi l’asse deve giacere sul piano orbitale dell’asteroide. Calcolando, infine, la differenza di magnitudine tra la visione polare (valore costante durante l’intera rotazione) e quella della visione equatoriale al massimo della curva di luce, si ottiene subito anche il rapporto tra b e c. Si usa la solita formula:
mP – mE = – 2.5 log (A(polare)/Amax(equatoriale)) = – 2.5 log (πab/ πac) = – 2.5 log (b/c)
Il “caso” è risolto completamente.
Come già detto, però, questa è una situazione del tutto peculiare, molto didattica, ma poco realistica. La situazione “normale” è decisamente più complicata. Ciò che capita è quanto raffigurato in Fig. 6.
L’inclinazione del’asse di rotazione sul piano orbitale è diversa da 0° e da 90° (o, se preferite, la latitudine, nel caso di orbita complanare con quella dell’eclittica). Tuttavia, dobbiamo notare due cose importanti. Anche in questo caso realistico, prima o poi, si avrà un’opposizione con una visione equatoriale (angolo di aspetto A uguale a 90°).
Se questa asserzione vi lascia un po’ dubbiosi, pensate alle stagioni terrestri. Esistono sempre due punti in cui l’asse di rotazione della Terra è perpendicolare al piano dell’eclittica e questi sono gli equinozi. Essi vi sono comunque, indipendentemente da quanto vale l’angolo tra asse ed eclittica. La visione polare è invece impossibile da ottenere e si ha soltanto un valore minimo di ampiezza, in corrispondenza, però, della posizione a 90° dalla visione equatoriale. In altre parole, il minimo della curva ampiezza-longitudine indica, ancora una volta, la longitudine del polo dell’asteroide. Nel caso terrestre questi sono i punti dei solstizi. Alcuni esempi di curve ampiezza-longitudine sono riportate nella Fig. 7.
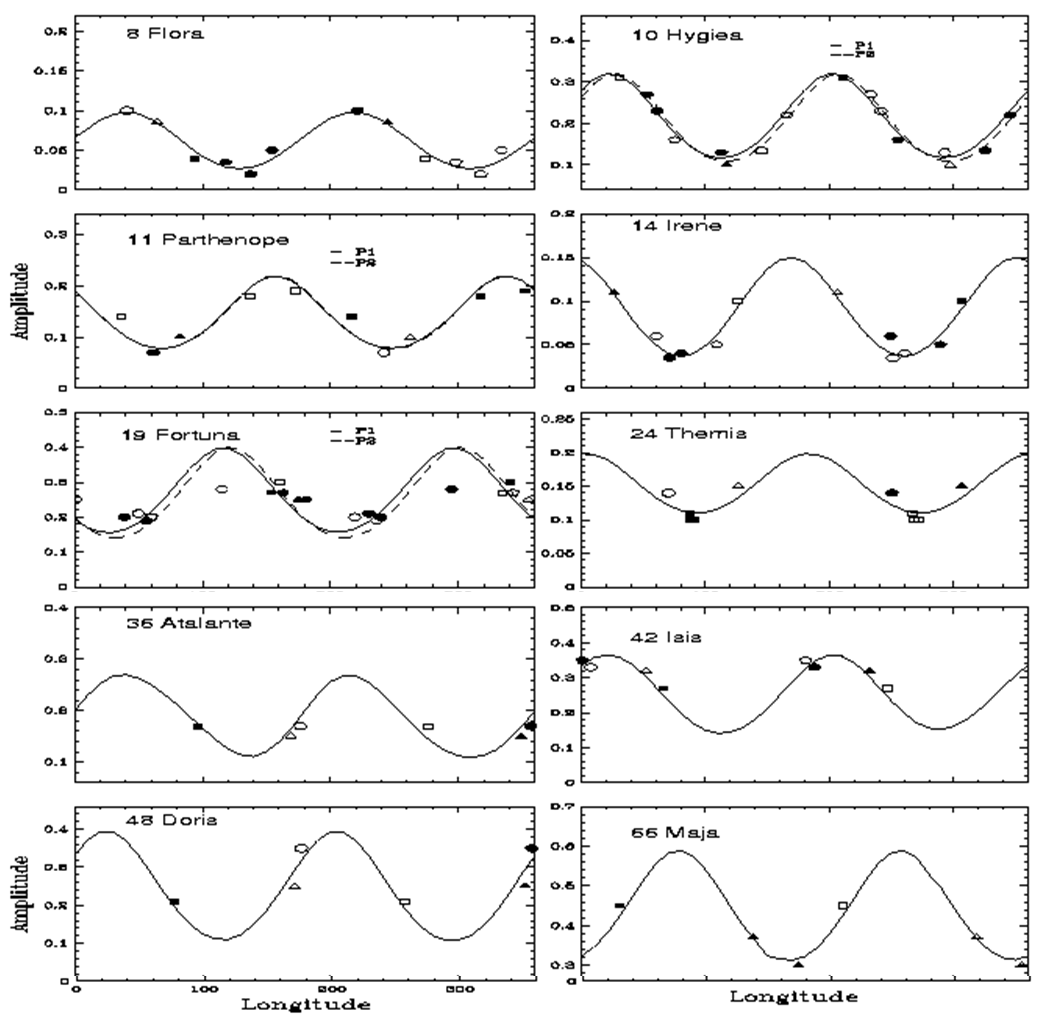
Possiamo calcolare, come al solito, il rapporto a/b, sfruttando l’ampiezza misurata nella visione equatoriale (che si ha sempre, ripeto). Resta più problematica la determinazione del rapporto b/c e della latitudine del polo. Ci aiuta la Fig. 8 che riporta la situazione per un’opposizione e per un orientamento qualsiasi dell’asse di rotazione. L’osservatore vede, in realtà, una proiezione dell’asteroide-ellissoide su un piano perpendicolare alla linea di vista. Essa si ottiene, visivamente, come la sezione perpendicolare di un cilindro ellittico che abbia la direzione Terra-asteroide come asse e che sia tangente all’asteroide.
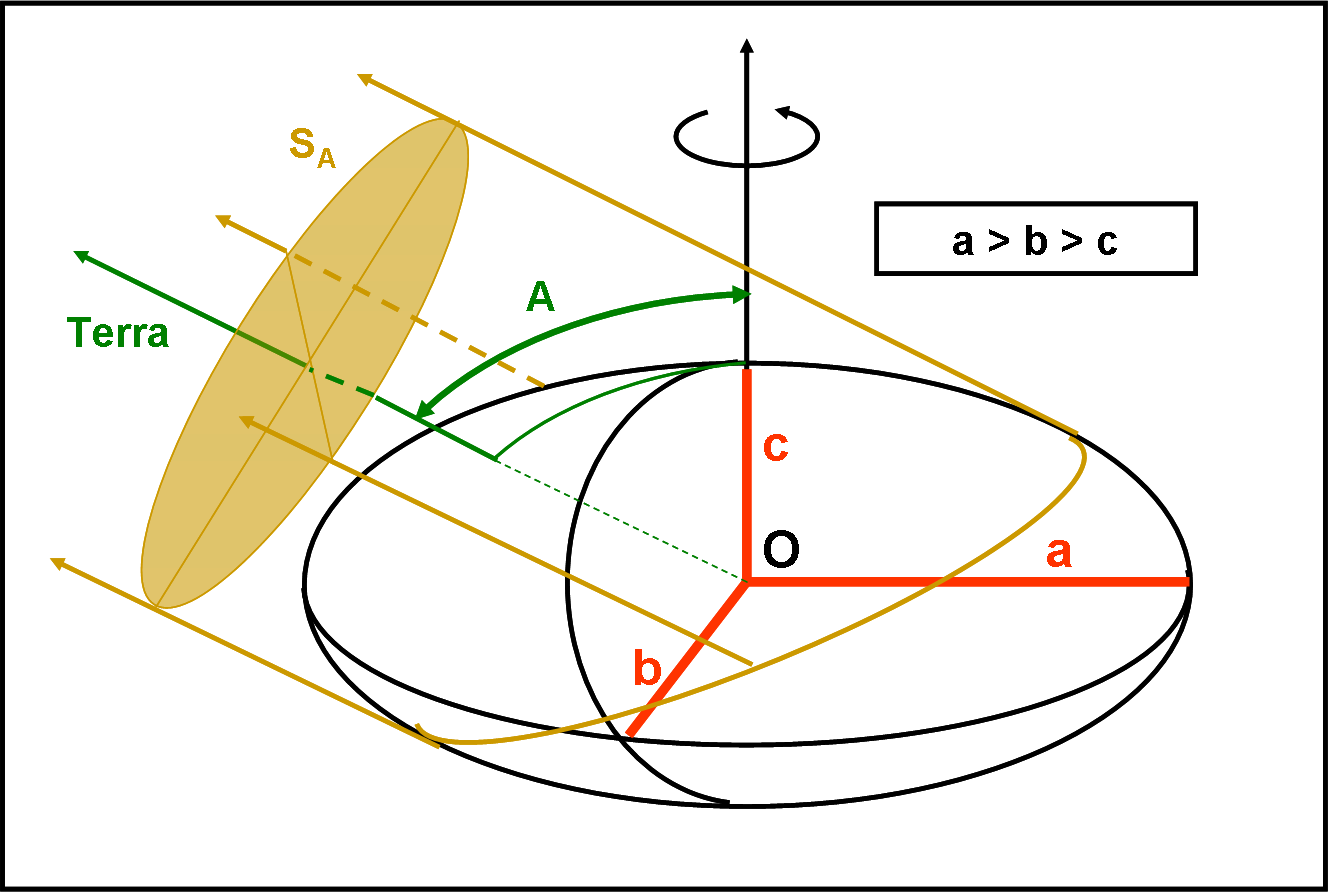
L’angolo tra asse del cilindro e asse di rotazione è proprio l’angolo di aspetto A. La proiezione è anch’essa un’ellisse, ovviamente, ma i suoi assi sono, momento per momento, delle funzioni abbastanza semplici che legano angolo di aspetto e rapporti tra i semi-asse dell’asteroide.
Particolare rilevanza hanno, ovviamente, quelli relativi al massimo e al minimo della curva di luce. Non intendo sviluppare le formule, in quanto approfittano di un po’ di trigonometria e di qualche passaggio più o meno noioso, ma posso assicurarvi che esiste una soluzione che dona sia la forma che i rapporti tra gli assi.
Abbiamo fatto qualche ipotesi restrittiva, ma le applicazioni ai casi reali confermano che l’approccio è più che sufficiente per una determinazione abbastanza accurata. I risultati ottenuti per Eros, Kleopatra e Vesta (anche se in modo più elaborato) sono perfettamente in accordo con quanto osservato “in loco” (Eros e Vesta) o attraverso le immagini radar (Kleopatra).
La determinazione dell’asse di rotazione resta, comunque, un po’ ambigua. In altre parole, esistono quasi sempre due soluzioni altrettanto valide. Questo fatto si può notare nella Fig. 9.

Qualsiasi sia la configurazione dell’asteroide nello spazio, la curva di luce non cambia se l’asse di rotazione descrive un cono circolare, di ampiezza uguale all’angolo di aspetto A.
Fortunatamente, questa enorme ambiguità si ha solo per una singola opposizione. Se ne abbiamo altre e raffiguriamo, nel piano longitudine-latitudine celeste, le circonferenze che hanno centro nella posizione dell’asteroide e raggio uguale all’angolo di aspetto, esse hanno due soli punti in comune (Fig. 10).
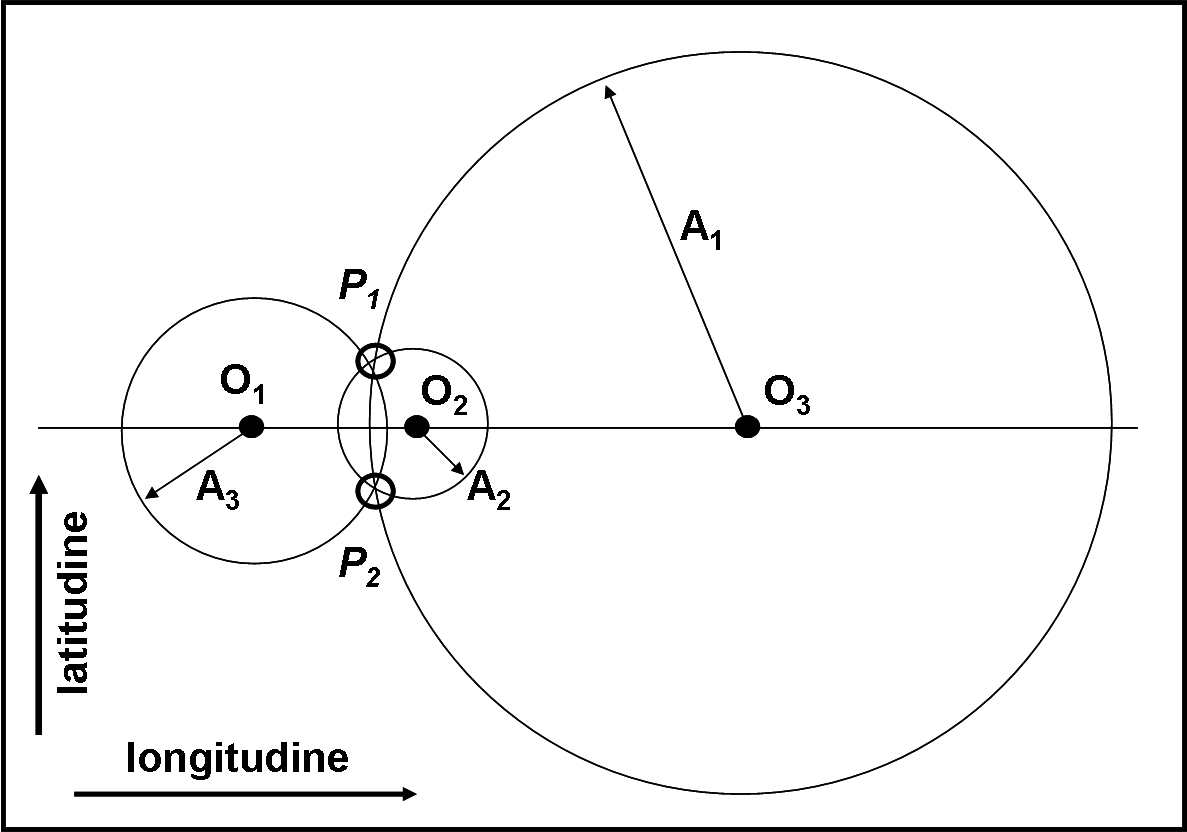
La loro longitudine e latitudine sono i possibili valori del polo dell’asteroide. In modo analitico questo fatto si traduce dicendo che l’angolo di aspetto è calcolato solo in valore assoluto (ossia può essere sia positivo che negativo, come già accennato in precedenza).
Per risolvere l’ambiguità, è necessario che l’orbita non sia complanare con l’eclittica e, magari, che sia anche piuttosto ellittica. In questi casi vi è una piccola differenza tra le due soluzioni: una delle due intersezioni è meno “buona” dell’altra.
Tuttavia, dato che gli errori sono molti (macchie di albedo, forma non assimilabile completamente a un ellissoide a tre assi, rugosità superficiale, effetto dell’angolo di fase solare sulla luminosità della superficie esposta all’osservatore (ossia l’ombra su una superficie convessa), ecc.), l’ambiguità è difficilmente risolta e le differenze riscontrate negli errori stimati per le due soluzioni sono comparabili o minori di quelli introdotti da altre cause.
In ogni modo, si ottengono valori più che accettabili per lavori di tipo statistico e anche per pianificare missioni spaziali dirette agli asteroidi, per le quali è necessario avere una stima dell’asse di rotazione e della forma.
Insomma, un giochino che penso sia piaciuto agli amanti della geometria. Gli altri portino pazienza e pensino a quante cose, nel Sistema Solare, si riescono a determinare da un punto di luce, solo perché è variabile.
Questo articolo è stato inserito nella serie "I Miei Amici Asteroidi"
QUI il report osservativo del "mio" asteroide 2813-Zappalà






8 commenti
Ah ah ah Enzone, indovina cosa ho (ri)trovato nella mia biblioteca?
Un simpatico volumetto del 1983 (edizioni "Il Castello") dal titolo: GLI ASTEROIDI.
Gli autori? Beh, Paolo Farinella, Paolo Paolicchi e ... Vincenzo Zappalà. Almeno uno dovresti conoscerlo ....
mamma mia... è vero! grande Alvy...
Caro Enzo, se mi conosci un poco sai benissimo che non pui cavartela affermando candidamente che:
"La rotazione intorno all’asse minore è comprovata dalla teoria e dalla casistica, e si lega a condizioni che si riferiscono al momento angolare".
Allora, diciamo che il momento d'inerzia I di un solido di rotazione dipende dalla massa M e dalle caratteristiche geometriche. Facciamo due casi semplici (le espressioni le ho ritrovate su internet perchè non le ricordavo):
I di un cilindro pieno omogeneo, rispetto all'asse longitudinale: (1/2)*M*R^2
I di una barra sottile piena omogenea, rispetto all'asse trasversale: (1/12)*M*L^2.
Esprimiamo la massa in funzione della densità (costante ed uguale per tutti) :
M = ρ*volume.
Facciamo ora l'ipotesi che R = L/10 (oggetto piuttosto allungato)
CILINDRO: I = (1/2)*ρ*π*10*R^5 = 5*ρ*π*R^5 rispetto asse longitudinale
CILINDRO: I = (1/12)*ρ*π*1000*R^5 = 83*ρ*π*R^5 rispetto asse trasversale
Se i due oggetti ruotano con la stessa velocità angolare ω , ottengo il seguente rapporto tra i momenti angolari m (m = I*ω) dei due oggetti:
m CILINDRO (longitud.) / m CILINDRO (trasvers.) = 0,06.
La rotazione intorno ad un asse trasversale assicura dunque un momento angolare maggiore (a parità di condizioni) rispetto alla rotazione rispetto all'asse longitudinale.
Questo bel polpettone, caro Enzo, mi è servito per arrivare alla domanda fatale:
maggiore momento angolare significa maggiore stabilità? Come si arriva, analiticamente, a tale conclusione? La grandezza che regala stabilità ad un sistema è l'energia potenziale; più è bassa, più stabile sarà il sistema.
In questo caso ho a che fare con un momento angolare e non vedo campi di forza, a parte l'autogravitazione; come si imposta l'energia potenziale del sistema? Insomma, come si dimostra il busillis?
Certo di averti scassato a sufficienza, ti auguro buona serata ....
Un'ideuzza mi sta spuntando nella capocchia!
Non è che ricadiamo nel ... ho quasi paura a pronunciare l'innominabile .... nel ... nel ... si, insomma .... nel VIRIALE? Ecco, l'ho detto, mi sento già meglio
caro Alvy,
bisogna andare per gradi.
Innanzitutto la rotazione è stabile se avviene attraverso uno degli assi principali d'inerzia. Quindi, teoricamente, potrebbero andar bene le tre rotazioni. Tuttavia, quella di massima momento d'inerzia è la più stabile. Si può dimostrare in vari modi, ma ti basti pensarla così: la sfera che ha come raggio il semiasse maggiore contiene completamente l'ellissoide d'inerzia, mentre quella che ha raggio un semiasse minore NON contiene l'ellissoide. Anche ad occhio si capisce la maggiore stabilità... Qualsiasi piccolo spostamento fa riallineare un oggetto che ha massimo momento d'inerzia, mentre lo stesso fa deviare velocemente l'asse se sta ruotando attorno a un asse maggiore...
Non c'è bisogno di calcolare energia, anche se volendo si potrebbe anche trovare qualche relazione. I calcoli, però, non sono banali e di carne al fuoco, ancora al sangue, ce n'è tanta... Direi che possiamo consideralo un risultato comprovato dalla realtà dei fatti...
Senza voler entrare in ambito analitico, ti voglio sottoporre – tanto per dialogare amichevolmente – l’idea che mi sono fatto.
Abbiamo un insieme di corpuscoli che stanno collassando gravitazionalmente per formare un oggetto di tipo planetario o satellitare. L’autogravitazione e gli urti reciproci cospirano ad indirizzare il collasso in modo da consegnarci un oggetto di una data forma e di una data velocità di rotazione intorno ad un dato asse.
Adottiamo il principio di economia su cui si basano le “scelte” operate dalla natura: qualunque sistema tende alla configurazione di minima energia che comporta la massima “stabilità” del sistema stesso. Cosa vuol dire stabilità? Beh, che si deve spendere molta energia per alterare lo status quo.
Sappiamo che la forma a cui compete il minimo valore di energia potenziale gravitazionale è la sfera: possiamo dunque pensare che la gravità agisca per raggiungere quell’obiettivo i tutti i casi. Minima energia potenziale, cioè grande stabilità, significa essere fermamente ancorati alla propria posizione: una sfera sul fondo di un profondo avvallamento può essere spostata ma ricadrà sempre nello stesso punto.
Ma, cosa occorre per definire completamente lo stato di un oggetto o di una particella? Posizione e quantità di moto. Nel caso del proto-oggetto collassante immaginato in quiete rispetto al mondo esterno possiamo sostituire la quantità di moto con il momento angolare, grandezza associata all’oggetto in rotazione.
Come si fa a rendere stabile un oggetto rotante? E poi, stabile cosa, visto che ora non ci sono posizioni da mantenere? Bene, in realtà qualcosa da mantenere c’è, ed è la direzione dell’asse di rotazione. Un elevato momento angolare garantisce una maggiore stabilità del sistema rotante: è il principio del giroscopio. Sappiamo che la forma a cui compete un elevato valore (il massimo possibile?) del momento d’inerzia è la barra rotante intorno ad un asse di simmetria trasversale: possiamo dunque pensare che la rotazione agisca per raggiungere quest’altro obiettivo i tutti i casi.
Sembra così che abbiamo due diversi orientamenti della natura, incompatibili: forma sferica e basse velocità di rotazione o forma ellissoidica ed alte velocità di rotazione?
Beh, si tratta di capire chi la vince! Queste due azioni agiscono contemporaneamente sulla scorta delle caratteristiche del costruendo oggetto: massa, direzione ed energia cinetica dei corpuscoli ecc.
Si possono avere:
- oggetti sferici come la Terra, grande massa ed, in rapporto, piccola velocità di rotazione.
- oggetti quasi sferici come Saturno, grande massa ma anche grande velocità di rotazione.
- oggetti oblunghi a forma di sigaro, piccola massa ed alta velocità di rotazione, ecc.
Può funzionare Enzo?
Il ragionamento funziona in linea di principio e, infatti, è confermato da grandi masse collassanti (sfera o sferoide di rotazione). Per gli asteroidi normali le cose sono ben diverse. Essi sono per lo più dominati dalle forze di stato solido per cui la gravità conta molto poco nella configurazione di equilibrio. Il fatto è che essi ottengono il loro momento angolare attraverso gli urti mutui e una rotazione qualsiasi tende a rilassarsi verso il massimo momento d'inerzia. Nei casi in cui gli oggetti sono formati da mucchi di sassi sotto l'effetto della gravitazione allora il momento angolare acquisito negli urti può portare a forme d'equilibrio più complesse come gli ellissoidi di Jacobi (a tre assi) o la fissione in un sistema binario. Chandrasekhar li aveva studiati in gran dettaglio... Se cerchi sul web penso che si trovi il lavoro originario del premio Nobel (a me sembra di averlo visto... e il titolo dovrebbe essere qualcosa intorno alle figure d'equilibrio dei fluidi...).
Insomma, le configurazioni che dici tu non sono incompatibili, dato che chi comanda la forma finale è solo il momento angolare e un suo eccesso va oltre allo sferoide di Mc Laurin e arriva a Jacobi e poi al sistema doppio (come alcuni asteroidi mostrano e -forse- moltissime stelle).
Grazie Enzo