Categorie: Fisica classica
Tags: baricentro centro di massa quiz
Scritto da: Vincenzo Zappalà
Commenti:11
SOLUZIONE della regata velica su Papalla **
Cominciamo proprio dall’inizio, con un concetto di geometria elementare, sicuramente noto a tutti. Come si definisce il baricentro di un insieme di punti?
Consideriamo il caso più semplice (Fig. 1, in alto), ossia i punti stiano tutti su una stessa retta che viene scelta come asse delle ascisse. Scegliamo anche un punto qualsiasi della retta come origine. Limitiamoci al caso di DUE soli punti (ma non cambierebbe niente se i punti fossero in numero ben più grande…).
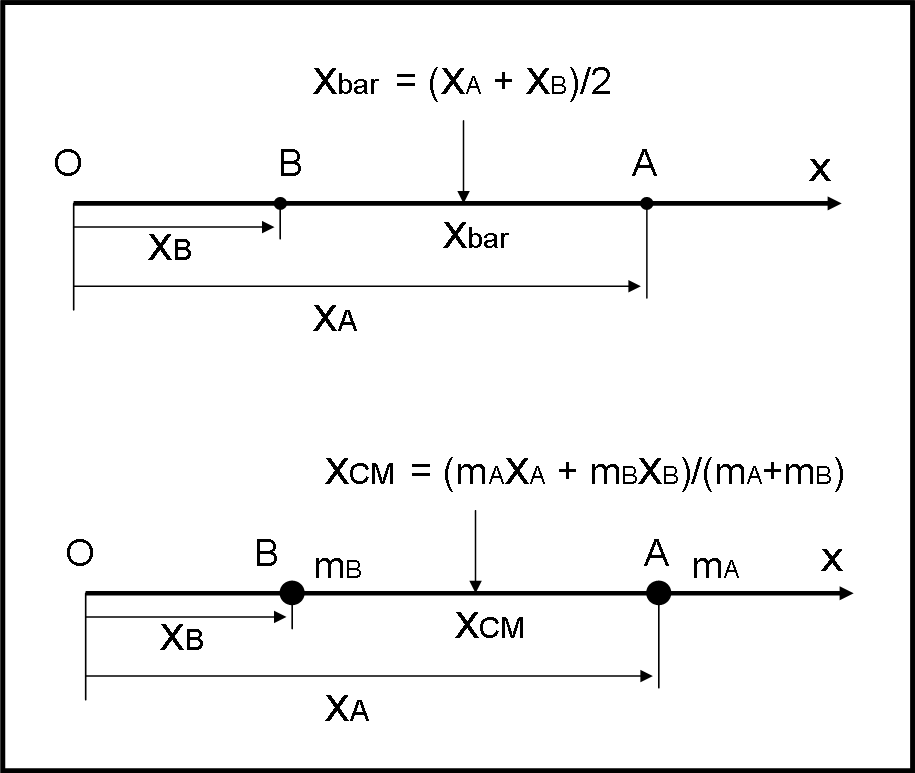
Rispetto all’origine O i due punti A e B hanno ascissa xA e xB. Il baricentro dei due punti è dato dalla somma delle due ascisse divisa per due, ossia:
xbar = (xA + xB)/2 …. (1)
In poche parole, non è altro che il valor medio delle ascisse dei due punti. Si otterrebbe una formula simile se considerassimo punti su di un piano (x,y): avremmo una formula come la (1) per le ascisse e una del tutto simile per le ordinate. Se, invece, i punti fossero N, la formula diventerebbe:
xbar = (xA + xB + …. + xN)/N …. (2)
Beh… queste sono formule conosciute fin dalle scuole medie.
La faccenda cambia di poco se facciamo diventare i punti A e B dei corpi dotati di una certa massa (Fig.1, in basso). Possiamo comunque definire la posizione del loro baricentro con una formula come la (1), solo che, adesso, bisogna moltiplicare ogni ascissa per la massa del punto-corpo corrispondente . La (1) diventa:
xCM = (xAmA + xBmB)/(mA + mB) …. (3)
Invece di baricentro si preferisce, spesso, chiamarlo centro di massa, ma il significato è lo stesso. Notate che la (3) diventa la (1) se le masse sono tutte uguali e unitarie…
Il centro di massa o baricentro di un sistema di corpi è estremamente importante dato che sappiamo bene come si possa sostituire l’intero corpo con un punto posizionato nel centro di massa che abbia come massa la somma di tutte le masse del sistema. Ricordiamo, ad esempio, il centro di massa di un sistema stellare binario. Ogni stella rivolve attorno al centro di massa del sistema, mentre quest’ultimo si muove di moto rettilineo uniforme.
Se considerassimo “fermo” il sistema, rispetto a un sistema di riferimento esterno, avremmo che le stelle continuano a rivolvere, mentre il baricentro sta fermo. E’ un punto estremamente importante perché può fare le veci dell’intero sistema e può agire solo lui in problemi di dinamica ben più complicati. In altre parole, i corpi che compongono il sistema possono muoversi come vogliono al suo interno, ma se non agiscono forze esterne, il centro di massa deve restare immobile.
Questo concetto è fondamentale e può anche dedursi tenendo conto della conservazione della quantità di moto del sistema e che, se la sua velocità è ZERO, tale deve rimanere senza l’intervento di forze esterne. In poche parole, le singole masse possono divertirsi a muoversi e a cambiare la posizione relativa del centro di massa del sistema, ma esso non può assolutamente muoversi rispetto a un sistema esterno e quindi la sua posizione xCM deve rimanere costante.
Fatte queste premesse, oltremodo semplici e ben conosciute, possiamo cominciare a risolvere il nostro papalproblema…
Il nostro sistema è composto da due sole masse: la barca di 100 kg e papallino di 50 kg. Come ben noto, possiamo benissimo sostituire i due corpi con i loro rispettivi baricentri, in cui sia concentrata l’intera massa del corpo. In Fig. 2 (a), disegniamo il sistema barca + papallino in modo schematico, inserendo i loro baricentri. Prendiamo come origine la poppa della nave O e, come asse, l’asse della barca. Il baricentro della barca sia B e quello di papallino sia A.
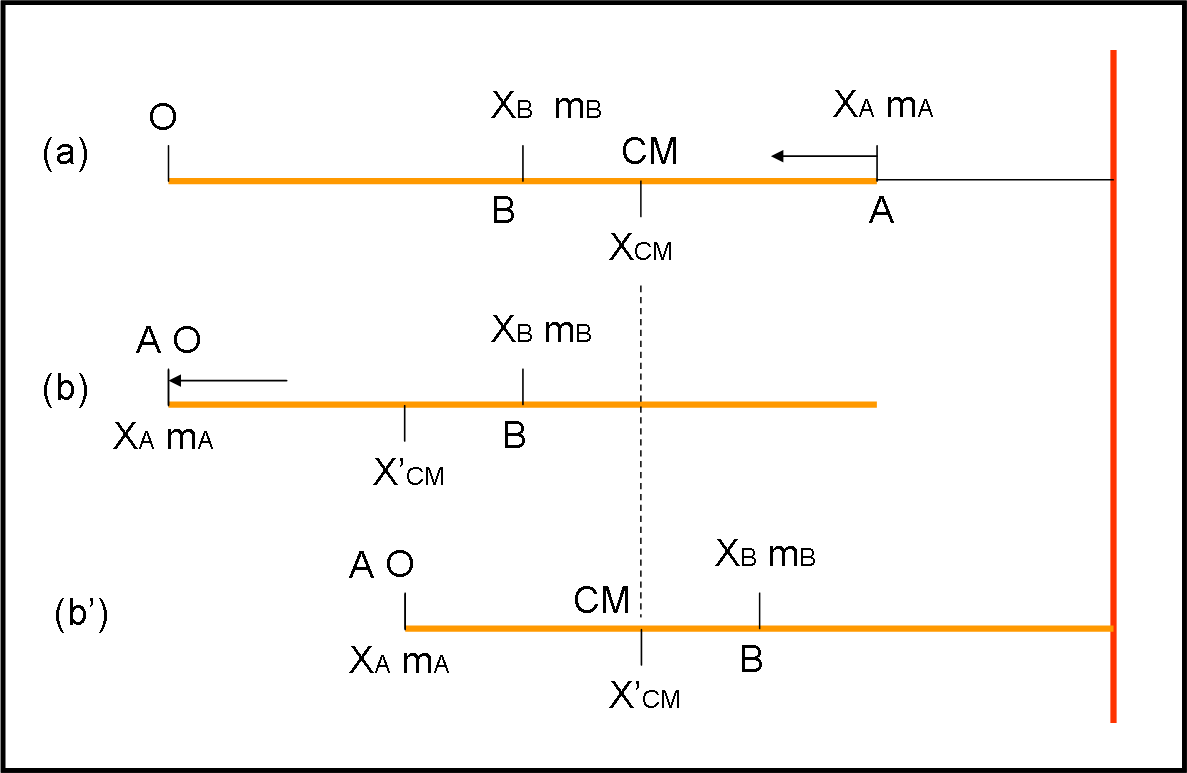
Ovviamente, dato che la barca è simmetrica lungo l’asse x, il baricentro xB (o centro di massa) della barca si trova a 3/2 = 1.5 m rispetto a O. Il baricentro di papallino si trova, invece, a una distanza xA = 3 m. Conosciamo anche la loro massa e, quindi, è immediato scrivere l’ascissa xCM del centro di massa (o baricentro) dell’intero sistema, attraverso la (3):
xCM = (xBmB + xAmA)/(mB + mA) = (1.5 x 100 + 3 x 50)/(100 + 50) = 2 m
Il centro di massa del sistema ha un ascissa xCM = 2m, ossia si trova a 2 metri dalla poppa della barca. Ricordiamo che il sistema deve stare fermo dato che non esistono forze esterne. In altre parole xCM deve rimanere sempre lo stesso, rispetto al pappalago, comunque si divertano a muoversi le masse che formano il sistema.
La barca non può muoversi, ma papallino sì. Ed ecco, allora, che si sposta senza fretta (a parte quella di sollevare al più presto la coppa di campione…) verso la poppa O (Fig 2 (b)). In poche parole, papallino cambia la sua ascissa da 3 a 0. Cosa succede facendo questa operazione? Beh… deve cambiare la posizione relativa del centro di massa del sistema, ma non certo la sua posizione rispetto al papallago, allo stesso modo di un sistema binario di stelle che non abbia velocità propria.
Calcoliamo allora la posizione del nuovo centro di massa x’CM, rispetto all’origine O (la poppa) che fa parte del sistema.
x’CM = (xBmB + xAmA)/(mB + mA) = (1.5 x 100 + 0 x 50)/(100 + 50) = 1 m
Il centro di massa si è spostato di un metro verso sinistra nel sistema di riferimento interno. Tuttavia, il centro di massa deve rimanere fermo rispetto al pappalago e quindi tutto il sistema barca + papallino deve spostarsi verso destra in modo da far coincidere la posizione del nuovo baricentro x’CM con la posizione di quello vecchio xCM. In altre parole, ancora, la distanza tra centro di massa e traguardo (sistema di riferimento esterno) deve rimanere uguale (Fig. 2 (b'))!
Notate che l'azione (b) e (b') avvengono contemporaneamente.
Attenzione: se avete problemi a immaginare questa azione, pensate di stare su una stella di un sistema binario. Per voi il baricentro del sistema si sposta in continuazione (un po’ lo vedete a destra e un po’ a sinistra), ma lui in realtà resta sempre fermo in un sistema di riferimento esterno (come il pappalago. le sue sponde e il traguardo).
La conclusione della “passeggiata” di papallino costringe la barca a spostarsi di un metro verso destra. Non un centimetro di più, però… I tre metri della barca, e quindi la variazione possibile del nuovo baricentro, non permettono uno spostamento maggiore.
Come si vede chiaramente, la soluzione può ottenersi facendo un calcolo a mente e trovando solo e soltanto la differenza tra la posizione del centro di massa iniziale e finale. Questa differenza è uguale e contraria allo spostamento del sistema rispetto al pappalago.
Chi vuole, può anche fare un breve studio di funzione per generalizzare la situazione allungando la barca e/o cambiando le masse in gioco. Oppure, vedere come varia lo spostamento del sistema verso destra per tragitti diversi di papallino. Funzioni veramente elementari…
Per concludere, direi che Paolo ha usato l’approccio migliore, anche se ha cercato di dimostrare contemporaneamente l’invarianza del baricentro, cosa che però è già insita nella sua definizione. Un esercizio di logica in più non fa mai male…
Anche se solo quattro amici hanno partecipato, devo dire che il concetto di base è stato, più o meno, compreso da tutti e quattro!
Qui potete trovare il testo del quiz
http://www.
E se siete interessati a conoscere o approfondire gli argomenti di fisica oggetto dei quiz, non potete perdervi "La Fisica addormentata nel bosco"
http://www.






11 commenti
Scusa Enzo, se uso questo post per una riflessione di carattere personale che spero possa servire da stimolo anche ad altri.
Giustamente tu affermi che nella soluzione del quiz ho cercato di dimostrare l'invarianza del baricentro.
Una simulazione che serve soprattutto a me stesso, poichè devo fare i conti con le mie lacune (il concetto di baricentro l'ho ricavato più dai ragionamenti, che non da quel poco che ricordo e che purtroppo per me non era affatto scontato o assodato).
(il concetto di baricentro l'ho ricavato più dai ragionamenti, che non da quel poco che ricordo e che purtroppo per me non era affatto scontato o assodato).
In passato, davvero non capisco perchè, ho litigato con la geometria, e tra i due ero io nel torto.
Mi sono trascinato per anni i postumi di questa lite, finchè grazie ai tuoi articoli ho compreso (almeno in parte) non solo l'importanza di una visione geometrica, ma la sua attinenza con il formarsi di schemi mentali che consentono di inquadrare i problemi.
Il mio uso delle figure, non vuole essere un'esposizione di conoscenze che non ho, ma il tentativo di comprendere ciò che prima mi sfuggiva, ossia un tentativo di rappresentare gli schemi mentali che cerco di adottare per affrontare il problema, nella consapevolezza che si può sempre migliorare, affinando l'interpretazione e le possibili soluzioni, o anche di rendersi conto dell'errore che si sta commettendo, che porta ad analisi e soluzioni errate.
Per fortuna con la logica non ho mai litigato, ma senza una visione generale del problema, anche la logica mostra i suoi limiti.
Non so proprio come ringraziarti perché quasi magicamente quello che prima era il mio punto debole (la visione geometrica) ora lo uso come strumento di analisi.
Mi scuso di nuovo per questo intervento un po' fuori tema, ma spero che questo possa servire da stimolo anche ad altri e altre......
A tal proposito, aggiungo solo che se uno che è uscito parecchi anni fa da scuola, con il mediocre voto di 40/60 (tutto sono tranne che un secchione), ogni tanto riesce a risolvere qualche quiz (altre volte non c'è verso, oppure pur essendo arrivato alla soluzione questa è più frutto di approssimazioni successive, che non di una reale comprensione del problema) questa strana idea sulla potenza della logica non è poi così insensata o riservata a pochi, anzi.....
Comunque, giusto per capirsi, voi non avete idea di quanti foglietti pieni di calcoli mi capita di produrre quando cerco una verifica matematica all'ipotesi che sto vagliando.
Spesso si può anche arrivare ad una soluzione geometrica del problema o solo logica, ma la sua plausibilità deve reggere anche dal punto di vista matematico.
Paolo
PS: Salutami Barbara, anche se non ci conosciamo, con l'augurio che le cose continuino a migliorare.
caro Paolo,
il tuo commento non è assolutamente fuori tema ed è utilissimo per comprendere come ci si avvicini sempre di più alla fantasia e al rigore della coppia matematica-fisica. La componente fondamentale è sempre la logica, senza la quale si può studiare quanto si vuole, ma si rimane sempre lontani dalle meraviglie che l'Universo e la Natura ci mostrano attimo dopo attimo. Con la logica, tutto riesce a prendere forma, sia una serie di formule sia una figura più o meno complessa.
Vorrei fare una scommessa... Se c'è una geometria complicata e poco intuitiva, a prima vista, è proprio il diagramma spaziotemporale di Minkowski. Tuttavia, esso è permeato di logica, anche se non immediata. Sono convinto che tu ne sarai uno dei più appassionati "amanti" e fruitori!!!!
Mi devi anche scusare se sovente non do il giusto rilievo al lavoro che svolgete. La tua soluzione della regata è ineccepibile e dimostra come tu abbia perfettamente digerito il concetto di quantità di moto e della sua conservazione. A tal punto, che sei riuscito ad arrivare alle proprietà del baricentro partendo da lontano. Un esempio di perfetta logica e di applicazione rigorosa.
Devo, però, fare un po' l'amico del giaguaro e cercare sempre la via più immediata e fisicamente (o matematicamente) semplice. La Scienza deve sempre cercare la semplicità, come tutti sappiamo molto bene.
Sono, però, contentissimo dei tuoi sforzi, mai casuali e sempre puntati allo scopo. Avessi avuto tanti allievi come te...
Faccio meno complimenti ad Alvy, dato che si vede che ha a disposizione un bagaglio di partenza già elevato. Lo "bastono" soprattutto quando si perde dietro a calcoli che poco contribuiscono alla comprensione di un certo fenomeno. Col tempo a disposizione e con le cose che ci sono ancora da imparare, reputo giusto, nel tempo in cui riuscirò a essere ancora abbastanza lucido, affrontare i concetti piuttosto che gli ornamenti che li abbelliscono. Un po' come Michelangelo (fatte le dovute proporzioni, ovviamente!!!), che reputava inutile rifinire una statua, ma riteneva sufficiente estrarre l'anima nascosta nel marmo...
Tuttavia, anche Alvy non può che regalarmi piacere nel come affronta i vari argomenti (ma non diteglielo, se no si monta la testa!)...
E poi tutti gli altri che a volte ci provano, a volte ci riescono e a volte preferiscono tacere, ma sono convinto che sono moltissimi quelli che affrontano gli esercizi e non certo pochi quelli che li risolvono (ma non si fidano tanto di loro...).
Insomma, magari rallentandoli, penso che continuerò nel proporre quiz di fisica classica, la base di qualsiasi teoria più moderna e mediaticamente accattivante!
Grazie per tutto il resto e vi posso confermare che le cose migliorano continuamente giorno per giorno, anche se lentamente...
Caro Enzo, ma la soluzione più semplice ed elegante è proprio quella che mi aspetto da te, per cui fai benissimo a giaguardare.
Non si finisce mai di imparare cose nuove!
Sai, a volte capita di veder ridurre anche la conoscenza a “competizione”.
Vi è un'idea piuttosto diffusa che la competizione sia quella con gli altri, in cui ognuno cerca di dimostrare di essere più bravo.
Per me invece la competizione è con se stessi, una sfida senza fine, da cui non si può uscire vincitori e proprio per questo si possono cogliere e costruire occasioni per crescere, ampliando comprensione e conoscenza.
Paolo
PS: Sulla geometria di Minkowski , vedremo, devo però trovare il tempo di rileggermi alcuni articoli precedenti e di digerire fino in fondo le derivate ed il concetto di funzione di una funzione (per esempio ai risultati del quiz sul naufrago sono arrivato in pochissimo usando il teorema di Pitagora ed andando per approssimazioni successive, ma non sono riuscito a fissare matematicamente la condizione, ossia quando si ha il tempo minore... poi leggendo la tua soluzione basata sullo studio delle funzioni, a cui ancora non sono arrivato, ho capito perchè!)
hai perfettamente ragione Paolo! Al limite, sono solo io, che mi arrogo il compito di voler insegnare, che posso essere più o meno bravo...
Al limite, sono solo io, che mi arrogo il compito di voler insegnare, che posso essere più o meno bravo... 
La scienza e il conoscerla non devono mai essere competizione, ma aiuto reciproco. Non mi sognerei mai di dare un "premio" a chi risolve prima e meglio un quiz. Come diceva il buon vecchio Einstein: "Tutto è relativo!" (se mi sentisse mi ucciderebbe). Vale di più un'intuizione, un semplice ragionamento, che una trattazione perfetta e rigorosa. Qui si gioca per imparare, ma guai a dire che esiste un "più bravo"!!!! La bravura è, appunto, relativa... Il vero premio si ha con se stessi e non c'è metro assoluto per misurarla. Può essere più meritevole uno che riesce a fare una radice quadrata che non uno che risolve un integrale triplo! Tutto dipende dalle condizioni al contorno e dalla volontà e impegno messi in gioco.
Per me siete tutti bravi ugualmente solo perché leggete e cercate di capire.
Tuttavia, anche Alvy non può che regalarmi piacere nel come affronta i vari argomenti (ma non diteglielo, se no si monta la testa!)…
già fatto!!

E dai Enzone, non pretendere troppo da me. Guarda che ho i miei bravi limiti!
Continuo a pensare che mi sopravvaluti (parecchio).
A dirla tutta, la soluzione della rotazione non mi sembrava affatto male. C'è da ammettere che, per far tornare i conti, si deve fare assegnamento sulla presenza di un agente esterno a cui cedere quantità di moto, vale a dire l'atmosfera, senza la quale .... no se puete far nada!
D'altra parte hai scritto che fino ad un attimo prima il vento soffiava (altrimenti che regata velica sarebbe) per poi cadere del tutto. Quindi l'atmosfera c'è! Ho pensato di utilizzarla per raggiungere l'obiettivo; tra l'altro la rotazione cade a fagiolo perchè consente di tagliare perfettamente il traguardo, sia pure di poppa.
E poi i polpi non si spostano forse nell'acqua grazie alla reazione provocata dall'espulsione di acqua dal loro sifone?
Mi sembra che concettualmente la mia soluzione non sia sbagliata; attendo però una tua conferma.
Infine, riguardo ai calcoli che spesso svolgo, sono il mio modo di pormi di fronte ai problemi. Non so, mi sembra di avere più chiaramente in pugno i concetti e devo dire che, a volte, è proprio svolgendo i calcoli che mi rendo conto di talune peculiarità concettuali.
caro Alvy,
no forze no rotazione... se c'era l'atmosfera non sarebbe stata Papalla... E poi non ti ricordi che i papallini non possono soffiare!!!!
Comunque, ne sto preparando uno niente male che spero ti metta in ... difficoltà!
sssshhhrrriii....
è il rumore delle unghie sul vetro ...
Pur di non darmi soddisfazione saresti disposto ad inneggiare agli psico-terroristi del GW!
... una regata velica senza vento ... i papallini non possono soffiare ... roba da matti!!
Eh si, aveva proprio ragione Calimero, sai quello tutto nero col guscio d'uovo per cappello.
ma no Alvy... tu non sei NERO, sei solo...

spor.....tivo?
ecco! Non mi veniva più la parola giusta... sportivo della mente, però! Dai, comincia a dedicarti alla papaslitta....
Dai, comincia a dedicarti alla papaslitta.... 