QUIZ: Rischio grosso per Papalla ***
Un asteroide di massa m considerevole (il suo diametro è di circa 20 km!) era in rotta di collisione con il pianeta. Sfortunatamente, la sua velocità non era elevata e, tenendo conto del contributo che la gravità del pianeta avrebbe impartito alla traiettoria del piccolo corpo planetario, la catastrofe sarebbe stata immane. Il suo parametro d’impatto d non lasciava speranze.
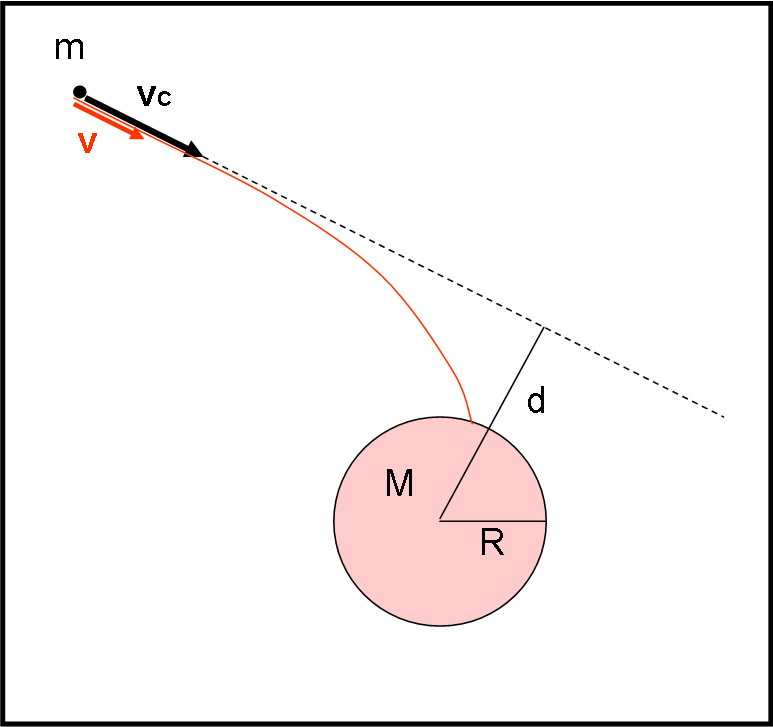
N.B.: Il parametro d’impatto (che già dovremmo conoscere attraverso la storia dell’atomo…) è la distanza (misurata perpendicolarmente) tra la direzione del moto dell’asteroide a grande distanza e il pianeta, come rappresentato in Fig. 1. Più professionalmente, questo vuol dire che si può trascurare l’energia potenziale gravitazionale nel sistema Papalla-asteroide.
Tuttavia, i governi papalliani hanno velocemente unito le proprie forze per cercare di aumentare la velocità v dell’asteroide. Per far ciò hanno dovuto calcolare la velocità minima vC che avrebbe permesso all’asteroide di sfiorare soltanto Papalla e poi proseguire nella sua corsa sfrenata (anche a costo di sradicare qualche albero troppo alto…). La Fig. 1 mostra la situazione dopo aver effettuato la correzione (eseguita a una distanza notevole dal pianeta) senza cambiare il parametro d’impatto. La curva rossa sarebbe stata la traiettoria prevista senza aver corretto la velocità originaria v.
L’impresa è riuscita perfettamente attraverso una serie di manovre di “spinta” ottenute utilizzando tutti i missili papalliani.
Vi chiedo semplicemente di trovare la formuletta che ci fornisce la velocità minima vC dell’asteroide, necessaria per scongiurare “al pelo” l’impatto catastrofico. Il diametro dell’asteroide può essere tranquillamente trascurato…
Ovviamente, su Papalla non c’è atmosfera…






53 commenti
Mah, io lascerei fare alla natura.
Un bel botto e ... addio papallotteri!
Ecco... sei il tipico TERRESTRE guerraiolo e distruttivo!!!
Quando dico sfiorare dico proprio sfiorare!!!! A costo di appiattire i papalliani o papalli che dir si voglia...
Ma no, lo sai che li adoro ... al forno con le patatine!
Ooooops, Enzo, ho letto solo ora la tua nota tecnica.
Eh si, avevo capito male. Pensavo che d dovesse restare costante e la traiettoria rettilinea.
Comunque Enzone, anche se devo ammettere che il verbo sfiorare ha un significato molto preciso, peraltro spesso usato a sproposito, quell'accidenti di segmento rettilieo che hai tracciato trae in inganno... mannaggia li pescetti ....
caro Alvy,
il segmento rettilineo serve solo a mostrare il parametro d'impatto che non cambia, perché si calcola quando il moto non è influenzato dalla gravità (vedi anche l'effetto Compton...) e la velocità è costante.
Troppa TV catastrofista?



O siamo solo reduci dalla fase "giramenti di papalli"...
Ok, va bene, va bene, torniamo a fare i seri...
Condizione necessaria perchè un oggetto (con traiettoria non impattante, ovviamente) non collida con il pianeta è che la sua velocità sia almeno pari alla velocità di fuga.
Per velocità di fuga si intende la velocità minima per sfuggire all'attrazione gravitazionale (sia che si tratti di pianeta, stella o altro), pertanto la ricaveremo ponendo l'energia cinetica dell'asteroide pari al potenziale gravitazionale.
Proviamo a mettere giù due righe...
1/2mv^2 = GMm/d
dove G è la costante di Gravitazione Universale,
M è la massa del pianeta,
m la massa dell'asteroide
proseguendo avremo che
v^2 = 2GMm/md = 2GM/d
e semplificando
v = (2GM/d)^1/2
che è la velocità minima cercata...
P.S. Alvy, i papalli vengono meglio in padella, almeno secondo una ricetta Andoriana molto in voga...
Inizialmente m ed M sono a distanza pressoché infinita, tanto che l’energia potenziale del sistema Ep → 0.
D’altra parte m ha una sua velocità V, mentre M lo consideriamo immobile: l’energia cinetica iniziale del sistema vale allora Ec = ½*m*V^2
Nel momento in cui m sfiora M, ovvero transita a distanza R dal centro di M, i valori delle energie divengono:
Ep = -G*M*m/R
Ec = ½*m*Vc^2
Per la conservazione dell’energia:
½*m*V^2 = ½*m*Vc^2 - G*M*m/R
Vc^2 = V^2 + 2*G*M*/R
Se V=0, Vc uguaglia la velocità di fuga Vf dal pianeta:
Vf = Vc = √(2*G*M*/R)
Caro Celty ..... con un pò di rosmarino?
Grassotteli come sono devono essere una prelibatezza ......
Alvy, spadellati con rosmarino e un filo d'olio non li vedo affatto male!
Va bene ma piantiamola qui, non vorrei che ad Enzo venisse un colpo apoplettico!
Sai, lui tiene molto ai papallini. Sospetto che abbia una relazione extra-coniugalterrestre con qualche papallina dotata di ... interessanti rotondità!
ma v non è uguale a zero... mi spiace ragazzi, ma l'energia non basta. A Celty, invece, ricordo che l'asteroide ha una sua velocità vC di partenza. Riflettete con calma... senza pensare a mettere al forno i nostri cari amici papalli... ingordi!!!!
aggiungo... Ricordatevi dell'effetto Compton ...
Enzo, sei sicuro? Secondo me non importa Vc iniziale, non dovevo mica calcolare il deltaV, ma la velocità finale. Quindi partire da 0, da 1 o da 2 non cambierebbe la V finale...
Quanto ai Papalli, ribadisco, meglio in padella!
Scusate ma l'età avanza ed il rincogl....... anche!
La prima volta ho affrontato un problema non richiesto da Enzo, presupponendo una traiettoria rettilinea di m con velocità variabile. Non so se lo svolgimento sia corretto (attendo notizie da Enzo).
La seconda volta ho trovato il legame tra la velocità iniziale e quella finale applicando il principio di conservazione dell'energia. Svolgimento formalmente corretto ma ... niente a che vedere con la richiesta del quiz.
Stavolta penso di aver colpito nel segno!
Dal momento che la velocità finale Vf di m che sfiora M deve essere la minima possibile che eviti la catastrofe, bisognerà che tale velocità sia la velocità di fuga dal pianeta. Per calcolarla si può applicare l'uguaglianza tra energia potenziale del sistema ed energia cinetica di m:
G*m*M/R = 1/2*m*Vf^2
da cui: Vf = (2*G*M/R)^2
Ora devo esprimere la velocità finale per mezzo della velocità iniziale Vc, cioè la velocità impressa inizialmente ad m perchè si verifichi la condizione appena imposta. Per fare ciò impongo la costanza del momento angolare del sistema, calcolandolo rispetto al centro di M. La traiettoria di m è curva ed m, una volta impostagli la velocità iniziale Vc, è libero di muoversi nel campo di M conservando il suo momento angolare.
Dunque:
m*Vf*R = m*Vc*d
da cui:
Vf = Vc*d/R
Sostituendo si ottiene:
Vc =√ [2*G*M*R/(d^2)]
N.B.:
per il calcolo del momento angolare di Vc, si può ragionare come segue.
α sia l'angolo tra la direzione individuata da Vc e quella che conduce al centro di M.
r sia la distanza tra m ed M all'istante in cui, ad m, viene applicata Vc. Si ha che r=d/sinα
Scomponiamo Vc nella componente radiale Vcr (stessa direzione di r) e tangenziale Vct (cioè normale ad r).
La componente radiale di Vc non dà contributo al momento angolare perchè il prodotto vettoriale tra detta componente ed r è nullo, avendo i due vettori la stessa direzione.
La componente tangenziale di Vc, pari a Vc*sinα, dà il seguente contributo:
m*Vct*r = m*(Vc*sinα)*(d/sinα) = m*Vc*d
... e adesso buonanotte a tutti!
per Celty,
ma è proprio la velocità iniziale che si chiede! Quella costante (ottenuta in qualche modo) che una volta che l'asteroide entra nel campo gravitazionale di Papalla gli permetterà , pur cambiando, di sfiorarlo soltanto...
per Alvy,
non ci siamo ancora. Perché mai vf dovrebbe essere una velocità minima? Si chiede la vC minima... non importa a che velocità l'asteroide sfiori Papalla, l'importante è che lo sfiori!
Mi sembra di essere stato chiaro: vC è la velocità che deve avere l'asteroide quando è ancora fuori dall'influenza di Papalla (o almeno lo possiamo considerare tale) e quindi viaggia di moto rettilineo uniforme. Poi tutto va di conseguenza...
Mi fa pensare che non abbiate letto l'articolo su Compton... male, male...
Dalla figura v è la velocità (bassa o quantomeno insufficiente) iniziale dell'asteroide, Vc è quella finale...
In mezzo c'è l'accelerazione impressa dai razzi (vettori) papalliani e l'accelerazione impressa dalla forza gravitazionale che porta Vc=vf.
P.S. Compton non è quello dell'effetto Compton, che descrive l'urto (anelastico) tra elettrone e fotone? Come lo posso inserire qui, che scontro NON ci deve essere?
No Celty,
vc è la velocità iniziale corretta molto prima che la gravità si faccia sentire. v è un ricordo che nulla c'entra con il problema... Basta considerare vc come la velocità costante di arrivo dell'asteroide, prima che la gravità papalliana faccia il suo corso.
Compton c'entra e come... non per niente l'effetto fionda si calcola nello stesso modo... fatte le dovute differenze pratiche.
Accidenti Enzo, hai ragione (ovviamente!)
Ho pensato che fosse sufficiente la condizione di tangenza del proiettile nei confronti del bersaglio; ma se il proiettile fugge via dopo aver sfiorato il bersaglio vuol dire che ha ancora energia che, nell'ottica del quiz, avrei dovuto risparmiare!
Allora, torniamo alla velocità finale, cioè tangente al pianeta.
Quand'è che questa velocità è la minima possibile, pur conservando la condizione di tangenza? Beh, quando rimane tangente al pianeta il più a lungo possibile, ovvero quando il moto è circolare a distanza R (raggio) dal centro del pianeta.
Ma allora devo imporre l'equilibrio tra gravità e forza centrifuga alla distanza R dal centro del pianeta:
G*M*m/(R^2) = m*(Vf^2)/R
Vf = (G*M/R)^0,5
da cui, imponendo la conservazione della quantità di moto secondo quanto già scritto precedentemente, ottengo che:
Vc =√ [G*M*R/(d^2)]
P.S.: effettivamente è più bassa di quella calcolata prima.
E' così?
sto godendo come un mandrillo!!!

No Alvy, non ci siamo ancora... L'asteroide non si sogna minimamente di ruotare attorno al pianeta. D'altra parte se scappa vuol dire che la sua velocità deve essere diversa da quella di rotazione... anche nel punto di tangenza...
Mah, pensavo che il potenziale gravitazionale si esprimesse anche a distanza r, infatti nella formula avevo inserito una generica distanza d > r, quindi la velocità di fuga in un punto a distanza d è inferiore che in un punto a distanza r (perciò sulla superficie).
Mi stai dicendo che devo complicare il tutto?
La soluzione si complica e non di poco...
Posta Vf la velocità di fuga a distanza r, la formula precedente diventa √(2GM/r).
Dovendo equiparare la velocità finale V alla velocità di fuga Vf devo andare a sommare alla velocità Vc l'incremento dovuto all'accelerazione di gravità.
Scriverò pertanto Vfinale=Vf=gt+Vc=√(2GM/r). (1)
Però non tutta la componente g è diretta in direzione del moto, quindi dovrò modificare la (1) in Vfinale=Vf=gt(cos α)+Vc=√(2GM/r) (2)
Sapendo che g=GM/d^2
la (2) diventa (GM/d^2)t(cos α)+Vc=√(2GM/r)
ossia
Vc=√(2GM/r) - (GM/d^2)t(cos α)
Ma è sicuramente più complicato ancora, dato che α è un angolo variabile (vale 0 a distanza infinita e 90 nel punto a distanza r in cui l'oggetto "sfiorerebbe" la superficie) ed anche la distanza d (da assimilabile ad infinito a 0), perciò mi fermo qui...
P.S. L'effetto fionda non è dato da una particolare traiettoria (iperbolica) in cui un oggetto di massa trascurabile rispetto al pianeta (es. le sonde Pioneer e Voyoger nei confronti di Giove), "ruba" momento (infinitesimo dato il rapporto di massa) al pianeta stesso?
vi ostinate con la velocità di fuga... perché mai? L'angolo conta ben poco e il tutto è decisamente più semplice...
L'effetto fionda è un caso particolare in cui si muove anche il pianeta. Ma la base è sempre la stessa: un urto che non è un vero urto... Ne avevo parlato a lungo in un articolo dedicato...
commento ulteriore: certe cose erano ben spiegate in un vecchio articolo (anzi una serie) che è stato forse snobbato?

Non è un'ostinazione, è solo una deduzione. Nel senso che se la velocità finale risultasse troppo bassa, l'oggetto impatterebbe. Per velocità più alte ma inferiori alla velocità di fuga avverrebbe la cattura (è quello che vogliono fare con le nuove missioni su Marte).
Si pensava quindi restasse valida la sola ipotesi che l'oggetto dovesse continuare per la sua strada.
E poi te lo immagini un satellite con perigeo =r?
Dovrebbero mettere perennemente un Papallo di vedetta: "Occhio che arriva! Chinate la testa!"
"Testa? QUALE testa?"
SPLAT!
Farebbero la fine dei pomodorini che attraversano la strada!
P.S. L'articolo non lo ricordo... Puoi metterci un link? Thanks!
http://www.infinitoteatrodelcosmo.it/2014/10/15/leffetto-fionda/ (bastava usare il motore di ricerca... )
)
Beh... un oggetto con perigeo (ma non è un perigeo, dato che non è in orbita!) uguale a R era già stato formulato per fare un canale di Panama nuovo di zecca ( e ne avevo anche parlato). E poi l'ho detto che dovevano schiacciarsi a terra (anzi a papalla)
e ne avevo anche parlato). E poi l'ho detto che dovevano schiacciarsi a terra (anzi a papalla) 
Quello lo avevo trovato (usando appunto il motore di ricerca), ma non mi era sembrato "calzante" per il nostro caso. Quanto al perigeo diventa tale se l'oggetto viene catturato, e se la velocità di "approccio" è inferiore alla velocità di fuga allora non potrà sfuggire ed entrerà in orbita. Mi ricordo l'articolo sul nuovo canale, ma alla fine l'oggetto non doveva sfuggire, ma "arenarsi", in modo da sfruttarlo come miniera...
caro Celty,
(1) l'approccio al problema è molto simile, te lo assicuro.
(2) perché mai dovremmo farlo entrare in orbita? Noi vogliamo solo che sfiori Papalla e continui per la sua strada. La parola perigeo non c'entra niente, quindi...
(3) Il problema in esame è ovviamente un caso teorico, senza atmosfera e senza altri intoppi. I problemi sono sempre così... e già creano difficoltà. Arenarsi o sfiorare è una differenza minima se ci portiamo in casi ideali come quello trattato.
Dai, ormai mi sono sbilanciato abbastanza.... e il problema, se lo leggi bene, chiede una cosa ben chiara.
Allora, ho cambiato approccio: )
)
Consideriamo l'energia TOTALE del sistema = Energia Potenziale (dovuta alla gravità) + Energia cinetica dell'oggetto e tale energia si deve conservare.
Perciò andiamo a scrivere:
1/2mVc^2 (energia cinetica) - GMm/r (energia potenziale gravitazionale)
che dovremo eguagliare alla energia nel punto di "sfioro", che ovviamente sarà esclusivamente *cinetica* in quanto l'energia potenziale si sarà convertita in cinetica e potremo considerarla pari a 0.
Scriveremo perciò 1/2mVc^2 - GMm/r = 1/2m(√(2GM/r))^2
Abbiamo posto per semplicità la velocità finale pari a quella di fuga (non vogliamo che entri in orbita, vero?
proseguendo passo passo:
m(1/2Vc^2 - GM/r) = 1/2m(2GM/r)
semplificando m:
1/2Vc^2 - GM/r = 1/2(2GM/r)
che diventa:
1/2Vc^2 - GM/r = GM/r
Vc^2 = 2 (GM/r + GM/r)
Vc= √(4GM/r) = 2GM/r
Dimmi che è giusto!!!
mi spiace... no...
ops, mi è saltata una radice... Vc= √(4GM/r) = 2√(GM/r)
Enzo, mi dici in cosa sto sbagliando?
Approccio, esposizione, formule o altro?
caro Celty,
non è vero che l'energia al momento dello "sfioro" sia solo cinetica, se mai è vero il contrario: era solo cinetica quando la velocità era vc. Ho, infatti, detto che vc è la velocità quando il corpo NON risente ancora della gravità papalliana...
Caro Enzo, sapessi che voglia di andare su Papalla e dare fuoco a tutto il pianeta!
Porca vacca, è di ghiaccio!
Conservazione del momento angolare:
m*Vc*d = m*Vf*R
nell'ipotesi che l'asteroide passi rasente al pianeta, ovvero alla distanza R.
Conservazione dell'energia:
½*m*Vc^2 = ½*m*Vf^2 – G*M*m/R
Risolvendo il sistema delle due equazioni si ottiene:
Vc = √ [(2*G*M*R)/(d^2-R^2)]
Se d=R la velocità da imprimere sarà Vc → ∞.
mmmmh, forse potrei fare come Archimede, sai quello degli specchi ustori ...
caro Alvy,
no , non bruciare Papalla!
Bene, sono contento e ti eleggo PAMEC di fiducia (Primo Assistente in MEccanica Classica). Il premio è un viaggio (di sola andata????) su Papalla!!!!
A parte gli scherzi... Bravo, complimenti. Non era facilissimo anche se gli urti non urti li avevamo già trattati...
Quello che mi fa girare le ... papalle è che ci ho girato intorno come e meglio dell'asteroide...
Male Alvy, molto male! Non sono affatto contento di te!

Mah!
Male perché devi andare su Papalla? ma dai... sono simpaticissimi e fanno tanti quiz!
Caro Enzo, sulla soluzione del problema devo ancora ragionarci.
Perciò per ora ho solo provato a inquadrare il problema.
La figura mostra come pur mantenendo invariata la traiettoria iniziale dell'asteroide, modificando la velocità iniziale l'esito è molto diverso (tra l'altro tra la seconda e la terza ipotesi la velocità iniziale cambia di poco).
http://www.astrobin.com/full/38903/M/
Qualche piccola considerazione:
La direzione del moto verso il pianeta è dovuta all'accelerazione centripeta (ossia alla forza di gravità) ed è sempre diretta verso il centro del pianeta (basta considerare una serie di cerchi concentrici, con relativi raggi, che identificano la distanza tra asteroide e centro del pianeta);
La velocità e la traiettoria iniziali dell'asteroide combinandosi con l'accelerazione centripeta, determinano l'esito finale;
Se consideriamo il sistema pianeta asteroide come un sistema chiuso, l'energia totale in gioco e la quantità di moto complessiva, devono mantenersi (anche se le due masse non si urtano fisicamente);
Guardando la figura mi sembra molto difficile che l'asteroide possa sfiorare la superficie del pianeta e poi allontanarsi (vedi esempio due, il pericolo sembra inizialmente scampato, ma poi...), al limite potrebbe essere possibile fare una cosa simile solo dopo oltre mezzo giro di boa.....ma qui serve la matematica per capire se è possibile.
Comunque esiste sicuramente una distanza minima che evita l'impatto e necessita di un minor apporto di energia per aumentare la velocità “iniziale” dell'asteroide (e penso che sia questa la soluzione da cercare e non la minor distanza a maggior velocità).
Paolo
PS: stasera provo a vedere se riesco a trovare la soluzione, sempre ammesso che il problema sia stato correttamente impostato.
potresti essere sulla strada giusta... Attendo speranzoso... Però, più che la quantità di moto si dovrebbe considerare... ssshhht!!!
Caro Enzo la soluzione a cui ho pensato differisce leggermente da quella di Alvy, per cui ne approfitto anche per chiarirmi alcuni dubbi.
Innanzitutto ho realizzato alcune figure, in maniera più precisa delle altre (questa volta sono frutto di qualche calcolo), dopodichè ho cercato di ragionare sull'energia necessaria per evitare lo schianto.
Se l'asteroide fosse fermo l'Energia totale tra asteroide e Pianeta sarebbe uguale all'Energia di Potenziale + l'Energia cinetica.
L'Energia di Potenziale è uguale a:
Epot= - GMm/r
L'energia cinetica a:
Ec= ½ mv^2
Per cui:
Etot = ½ mv^2 – GMm/r
Ora per sfuggire a un inevitabile impatto, l'asteroide dovrà usare altrettanta energia, per cui la sua Energia cinetica dovrà almeno eguagliare quella dovuta al campo gravitazionale:
½ mVct^2 = ½ mVf^2 – GMm/r
Vct^2 = Vf^2 – 2GM/r
Vf è la velocità (istantanea), che varia in funzione del raggio, se questo diminuisce aumenta l'energia cinetica, ossia la velocità.
Vct è la componente della velocità iniziale Vc, perpendicolare al raggio (il segmento d che separa l'asteroide dal centro del pianeta).
http://www.astrobin.com/full/38903/N/
Ho scelto di usare questa componete del moto, perchè è quella che può offrire o meno qualche chance di evitare la catastrofe.
Se la traiettoria iniziale dell'asteroide fosse in direzione del centro del pianeta, aumentare la sua velocità accelererebbe solo lo schianto, per cui conta anche la traiettoria iniziale dell'asteroide prima di venir catturato dal Pianeta.
Scomponendo il vettore velocità usando il raggio e la sua perpendicolare, come assi di riferimento, la componente Vcr essendo parallela al raggio, porta l'asteroide verso il centro del pianeta (che è quello che si vorrebbe evitare), non solo, in un prodotto vettoriale se i due vettori sono paralleli il risultato si annulla, ossia è uguale a zero.
Durante l'avvicinamento al Pianeta la sua quantità di moto varia, ma non varia il momento angolare, poiché la Forza a cui viene sottoposto l'asteroide è sempre parallela al raggio, per il suo Momento è uguale a zero (grazie al prodotto di vettori paralleli).
IL momento angolare è uguale a.
L = r Λ q = r Λ mv =r mv sinϑ
Dato che la velocità dell'asteroide continua a variare, se considero le velocità istantanea come la perpendicolare al raggio in un dato punto (tangente ad un punto di un cerchio, o anche derivata dello spazio rispetto al tempo), l'angolo ϑ è sempre di 90°, per cui il suo seno vale 1.
Quindi:
L = =r mv
http://www.astrobin.com/full/38903/O/
Questa figura mostra solo il movimento rotatorio, mantenendo l'asse x sempre parallelo al vettore velocità (gli assi ruotano).
http://www.astrobin.com/full/38903/P/
Dato che L in questo caso è costante, il momento angolare dovrebbe risultare lo stesso sia quando l'asteroide era alla distanza d, sia quando è ad un distanza minore dal Pianeta:
m Vct d = m Vf r
Vct d = Vf r
Vct d/r = Vf
Sostituisco il valore trovato nell'equazione dell'energia:
Vct^2 = (Vct d/r )^2 – 2GM/r
Vct^2 = Vct^2 d^2/r ^2 – 2GM/r
Vct^2 + 2GM/r= Vct^2 d^2/r ^2
Vct^2 r ^2 + 2GMr = Vct^2 d^2
2GMr = Vct^2 d^2 - Vct^2 r ^2
2GMr = Vct^2 (d^2 - r ^2)
2GMr/(d^2 - r ^2) = Vct^2
Vct = (2GMr/(d^2 - r ^2))^1/2
Dall'equazione trovata si evince che conviene intervenire per aumentare la velocità quando l'asteroide è molto lontano, infatti più è alto questo risultato (d^2 – r^2) minore è la velocità Vct richiesta.
Cosa succede quando d = r l'ha già raccontato Alvy (crash).
L'unica vera differenza è che io ho preso in considerazione solo la componente trasversale di Vc, per cui alla fine la velocità Vc dipende dall'angolo iniziale tra il vettore Vc e il raggio (ossia dalla traiettoria iniziale dell'asteroide).
Per esempio se la componente Vct tende a zero o ad un numero molto piccolo (traiettoria diretta verso il Pianeta), Vc corrispondente tende a infinito.
In ultimo, senza intervento Papalliano, con velocità iniziale Vo non alterata da papallici interventi la catastrofe era inevitabile.
http://www.astrobin.com/full/38903/Q/
PS: Non so se è coretto o meno usare solo la componente trasversale della Velocità...
Paolo
caro Paolo,
il risultato è ovviamente giusto... ma non serve studiare come varia la velocità durante l'avvicinamento. L'importante è solo conservare energia e momento angolare. E quindi può bastare considerare la velocità tangente a Papalla che è, ovviamente, quella del minimo avvicinamento.
In generale,però, è giusto considerare solo la velocità trasversale, dato che l'altra componente dà momento angolare nullo.
OK!!!!
Per esempio se la componente Vct tende a zero o ad un numero molto piccolo (traiettoria diretta verso il Pianeta), Vc corrispondente tende a Vcr e non a infinito come erroneamente scritto.
Ciao Paolo, scusa se m'intrometto prima che intevenga Herr Professor.
Tu hai inizialmente impostato la formula della conservazione dell'energia del sistema. Un istante dopo l'introduzione della velocità "corretta" Vc (intendo corretta dall'intervento dei papalli) l'energia totale è solo quella cinetica, perchè i due corpi sono ancora molto distanti e l'energia potenziale gravitazionale del sistema è prossima a 0.
Nell'istante finale, quando cioè l'asteroide rasenta il pianeta, esiste sia l'energia cinetica dell'asteroide che l'energia potenziale del sistema. Tu le hai correttamente portate in conto.
Attenzione però, perchè l'energia non è un vettore, come sicuramente sai, ma uno scalare. Si deve quindi prendere in considerazione l'intero modulo del vettore velocità (elevato al quadrato). Se tu consideri solo una parte del modulo non stai applicando il principio di conservazione dell'energia, ma un principio di .... parziale conservazione, se così posso dire, che in realtà non conserva nulla!
In attesa delle scudisciate del Grande Capo, ti saluto caramente.
Ciao Alvy, quale intromissione ?
Come dicevo ne approfitto per chiarirmi alcuni dubbi.
Hai ragione, ma il mio intento era proprio quello di individuare solo quella parte di energia cinetica che determina un movimento capace di contrastare l'attrazione gravitazionale, ossia non parallelo al raggio (ossia di tener conto della traiettoria iniziale dell'asteroide).
Se la traiettoria dell'asteroide fosse diretta fin dall'inizio verso il centro del pianeta, che me ne faccio di tutta quell'Energia cinetica in più (aumento della velocità), dato che accelererebbe solo il disastro?
Il problema è anche che senza scomporre il vettore velocità ho parecchie difficoltà ad attribuire a sinϑ il valore di 1, dato che, solo se l'angolo è di 90° sinϑ = 1 :
L = r mV sinϑ = r mV
Per giustificare la perpendicolarità rispetto al raggio, ho usato la componente trasversale del vettore V, che poi è anche la tangente a quel punto di un cerchio il cui centro coincide con quello di gravita.
Tu come fai per eliminare sin ϑ?
Paolo
Dice bene Alvy (grrrr ).
).
Dunque Paolo,
devi considerare sia energia che momento angolare al momento in cui si ha vc. In quella situazione l'energia è solo cinetica. Il momento angolare è proprio m vc d, dato che r sin(alfa)= d, sempre, lungo la traiettoria non disturbata.
Assodato questo, basta dire che l'energia totale dell'asteroide deve conservarsi e quindi al termine di solo energia cinetica si deve aggiungere anche il termine di energia potenziale gravitazionale. Dato che vogliamo la tangenza vf deve essere perpendicolare al raggio R. Ma poco importa, dato che l'energia è uno scalare come dice Alvy.
Ma anche per il momento angolare poco importa la direzione di v, dato che non vi sono forze esterne (a parte la gravità che dà SEMPRE momento nullo) e quindi deve conservarsi. Nel caso di tangenza, velocità critica. quest'ultima è proprio perpendicolare e quindi il momento è m vf R.
Tu hai trovato il risultato corretto, proprio perché la velocità alla tangenza è tutta trasversale.
Paolo, puoi vedere le cose in questo modo, più generale.
Immagina di considerare un asteroide in viaggio verso il Sole e di considerare il suo moto in due diversi istanti A e B.
Immagina di conoscere la massa dell'asteroide e la sua velocità (modulo e verso) nell'istante A, oltre alla distanza dal Sole in A e B.
Vuoi determinare la velocità dell'asteroide quando giunge in B.
Come fare?
Se applichi il principio di conservazione dell'energia (che è uno scalare) puoi senz'altro ricavare Vb, ma solo il suo modulo! Non puoi cioè determinarne il verso.
Se applichi la conservazione del momento angolare (che è un vettore) puoi ottenere le informazioni che ti mancano. In pratica puoi determinare il modulo del momento in A (conosci tutte le variabili in gioco) e quel valore sarà lo stesso in B. Quello che calcoli in B è però il valore Vb*sinα (essendo α l'angolo tra la direzione di Vb ed il vettore distanza asteroide-Sole). D'altra parte è solo la componente tangenziale del vettore Vb (Vb*sinα) a dare contributo al momento.
Per ricavare Vb devi ricordarti allora della conservazione dell'energia, che Vb ti aveva già fornito; ora puoi ricavare anche α, cioè la direzione di Vb ed avrai tutte le informazioni cercate.
Insomma nè l'uno nè l'altro principio, da soli, ti possono dare tutte le informazioni.
Spero di non averti confuso le idee
Che vuoi, la natura è fatta così ...
P.S.: riguardo alla natura scalare dell'energia, credo che tragga in inganno il fatto che nell'energia cinetica compaia la velocità, la quale è immediatamente associata ad un vettore.
In questo caso devi "spersonalizzare" la velocità considerandola solo un numero: un numero non ha componenti, devi prenderlo così com'è, "tutto insieme".
Ah dimenticavo.
Non vorrei passare da maleducato nei confronti di Enzo, il quale mi ha salutato con un gutturale grrr.
Ricambio allora con un leggiadro prrr ...
Grazie a entrambi.......... lo dicevo che dovevo chiarirmi dei dubbi.
Provo a ricapitolare giusto per vedere se ho davvero compreso il mio errore.
Quando l'asteroide è in d, la sua energia cinetica è quella che è, e vale 1/2 mv^2.
Come questa energia verrà spesa durante l'avvicinamento al Pianeta dipende invece dall'angolo tra la traiettoria iniziale dell'asteroide e il raggio (che congiunge centro asteroide, centro Pianeta).
Se cerco la velocità tangenziale Vf, questa è perpendicolare al raggio, per cui il seno dell'angolo vale 1, quindi il momento angolare vale L= m vf r.
Continuo però a non comprendere perchè all'inizio d= r sin (alpha).
Più che mille parole la figura mostra la traiettoria dell'asteroide non disturbata (ho annullato la gravità, ossia il suo percorso non è disturbato), ma.....
http://www.astrobin.com/full/38903/R/
Continua a sfuggirmi qualcosa....
Paolo
Si Paolo.
Attenzione alla “spesa energetica” come l’hai definita. L’energia nel suo complesso si conserva, parlando ovviamente di sistemi chiusi ed isolati, come nel nostro caso in cui sono presenti solo l’asteroide ed il pianeta.
In qualunque punto si trovi l’asteroide è SEMPRE presente anche l’energia potenziale gravitazionale asteroide-pianeta. Quando Enzo dice di non considerarla intende dire che, data la distanza tra i due corpi, il suo valore è trascurabile. Trascurala pure analiticamente, ma non concettualmente!
Quindi l’energia iniziale totale del sistema (cinetica+potenziale) si mantiene sempre costante pur nelle reciproche trasformazioni cinetica-potenziale e viceversa, secondo che l’asteroide si allontani o avvicini al pianeta.
A ben vedere l’energia totale dipende da pochi parametri variabili:
- La velocità dell’asteroide (modulo!)
- La distanza tra i due oggetti.
Non c’è altro; ovviamente considero il pianeta immobile, altrimenti ci sarebbe da portare in conto anche la velocità del pianeta. La cosa importante è che non ci sono angoli da considerare.
Quando scrivi che d=r*sinα non fissarti su r*sinα ma su d!
Variare α in fondo significa variare d. Prova a considerare gli infiniti vettori Vc che hanno lo stesso punto di applicazione e tutte le possibili direzioni. Cosa cambia tra un vettore e l’altro? Semplicemente d.
Dalla formula risolutiva si vede come, variando d, varia ovviamente il modulo di Vc.
Vc = √ [(2*G*M*R)/(d^2-R^2)]
Se d aumenta (se cioè aumenta α) Vc diminuisce, essendo il vettore orientato sempre più lontano dal pianeta.
Grazie Alvy, la prima parte quella dell'energia l'ho data per scontata, ossia che quella relativa all'attrazione gravitazionale (cinetica e potenziale) sia trascurabile, ma non nulla.
La seconda parte è quella per me problematica.
Comunque penso di aver capito, l'informazione sul vettore r di riferimento è d con il suo angolo, se d inziale cambia, significa che l'angolo inziale è diverso, per cui la formula finale Vc = √ [(2*G*M*R)/(d^2-R^2)] già contiene tale informazione ossia il valore inziale di d.
Paolo
Paolo... ma r sin(alpha) vale proprio d dato che hai un triangolo rettangolo...
Ho capito l'errore!!!! quello che tu segni come d è quello che chiamo r. d è il parametro d'impatto, ossia la distanza tracciata perpendicolarmente tra asteroide e retta passante per Papalla e parallela alla traiettoria rettilinea iniziale dell'asteroide! O, se preferisci, tra il centro di Papalla e la traiettoria iniziale dell'asteroide (vedi figura dell'articolo).
Per la miseria io indicavo come d il raggio inziale r, invece d è proprio quello che nella figura che ho realizzato ho definito come sin (Alpha).
Quindi d= r sin (alpha).
D'altronde la tua figura indicava come d non certo il raggio inziale che congiunge asteroide e centro di Papalla
Ora tutto torna ed i dubbi sono svaniti
Mi sento un pò come quello che non andava dal dottore, ma si curava con l'enciclopedia medica, finchè non è morto a causa di un errore grammaticale
Paolo
Ottimo Paolo!!!
 Io ne faccio talmente tanti... e se non ci fossi tu ad accorgertene....
Io ne faccio talmente tanti... e se non ci fossi tu ad accorgertene.... 
D'altronde quando ci si avvicina a Papalla si fa in fretta a prendere fischi per fiaschi...
Mi spiace solo di non essermi accorto prima dell'errore di sbaglio...