Categorie: Relatività
Tags: Minkowski quiz relatività speciale velocità della luce
Scritto da: Vincenzo Zappalà
Commenti:16
QUIZ: la velocità della luce è relativa? ***
Prendiamo un’asta rigida molto lunga. Mettiamo una lampadina a un estremo dell’asta e uno specchietto all’altro estremo. Accendiamo la lampadina e vediamo il tempo che impiega la luce a tornare indietro. Facciamo molti tentativi accorciando e allungando l’asta fino a che il tempo impiegato non sia esattamente 2 secondi. A questo punto, non ci resta che misurare l’asta che (casualmente…) risulta uguale a 299 792.458km. Possiamo, perciò, dire che la luce ha percorso 599 584.916 km in due secondi. Basta dividere per due e otteniamo che la velocità della luce è 299 792.458 km/sec. Magnifico! Abbiamo calcolato sperimentalmente la velocità della luce. Possiamo introdurre le nostre unità di misura di spazio e di tempo, assumendo che l’unità del tempo sia un secondo e l’unità dello spazio sia 299 792.458 km. In questo sistema la velocità della luce è uguale a 1. In poche parole dire 299 792.458 km/sec equivale a 1 nel nuovo sistema di riferimento. Abbiamo solo cambiato le unità di misura, tutto qui…
Siamo molto fieri dello strumento di misura che abbiamo costruito e vogliamo farlo vedere in funzione ai nostri amici. Oltretutto, sappiamo molto bene che la velocità della luce è una costante per qualsiasi sistema di riferimento. Eseguiamo, allora, il nostro esperimento viaggiando a una velocità di 0.6 (con le nostre unità di misura), ossia di 179 875.475 km/sec rispetto ai nostri amici che si considerano fermi. La velocità della luce NON deve cambiare secondo quel genio di Einstein. I nostri amici, sparsi nello spazio, hanno degli orologi perfettamente uguali ai nostri (lo abbiamo controllato attentamente) e non devono fare altro che misurare il tempo di andata e ritorno della luce della nostra lampadina. Noi sappiamo benissimo che il risultato deve essere uguale a 2 secondi.
Ciò che succede in realtà è molto imbarazzante… Il tempo segnato dai nostri amici non è assolutamente 2 (come previsto e provato ripetutamente da noi)… Accidenti! Loro concludono che la velocità della luce è nettamente diversa, dato che hanno osservato distintamente che per andare fino allo specchietto e tornare indietro la luce ha impiegato un tempo diverso.
Ovviamente, ci prendono in giro e ci canzonano in tutti i modi! Noi siamo sicuri del nostro strumento di misura e glielo prestiamo per provarlo direttamente. Riprendiamo il nostro viaggio e guardiamo cosa succede, misurando il tempo di andata e ritorno della luce. Accidenti! Hanno ragione loro! Che errore clamoroso abbiamo fatto. Sarà colpa dell’orologio o dell’asta? Non sappiamo, ma quando “riusciamo” a incontraci ci chiedono immediatamente scusa. “Avevate ragione voi”, ci dicono, “il vostro strumento funziona perfettamente e abbiamo misurato che la velocità della luce è proprio uguale a 1. Vorremmo stare zitti e incassare il successo… ma non ci sentiamo di farlo: sarebbe troppo disonesto.
Rimaniamo tutti ammutoliti. Poi, però capiamo che ancora una volta è un problema di relatività della simultaneità…
Vi chiedo di disegnare le due figure, sempre con il nostro sistema in movimento, e trovare, graficamente, quanto tempo impiega la luce per andare avanti e indietro sull’asta rigida, se il fenomeno viene visto dal sistema esterno a quello che esegue l’esperimento (una volta quello considerato fermo vede l’esperimento fatto nel sistema in moto e l’altra volta il sistema in movimento vede l’esperimento fatto nel sistema considerato fermo). Basta che mi diciate quanto tempo impiega apparentemente la luce a percorrere l’asta avanti e indietro… tutto qui. Però, non usate le formule se no sarebbe troppo facile…
Nella Fig. 1 riporto già il diagramma da usare per entrambi i test. Ciò che ho disegnato basta e avanza: la retta che indica il nostro spostamento e la curva di calibrazione.
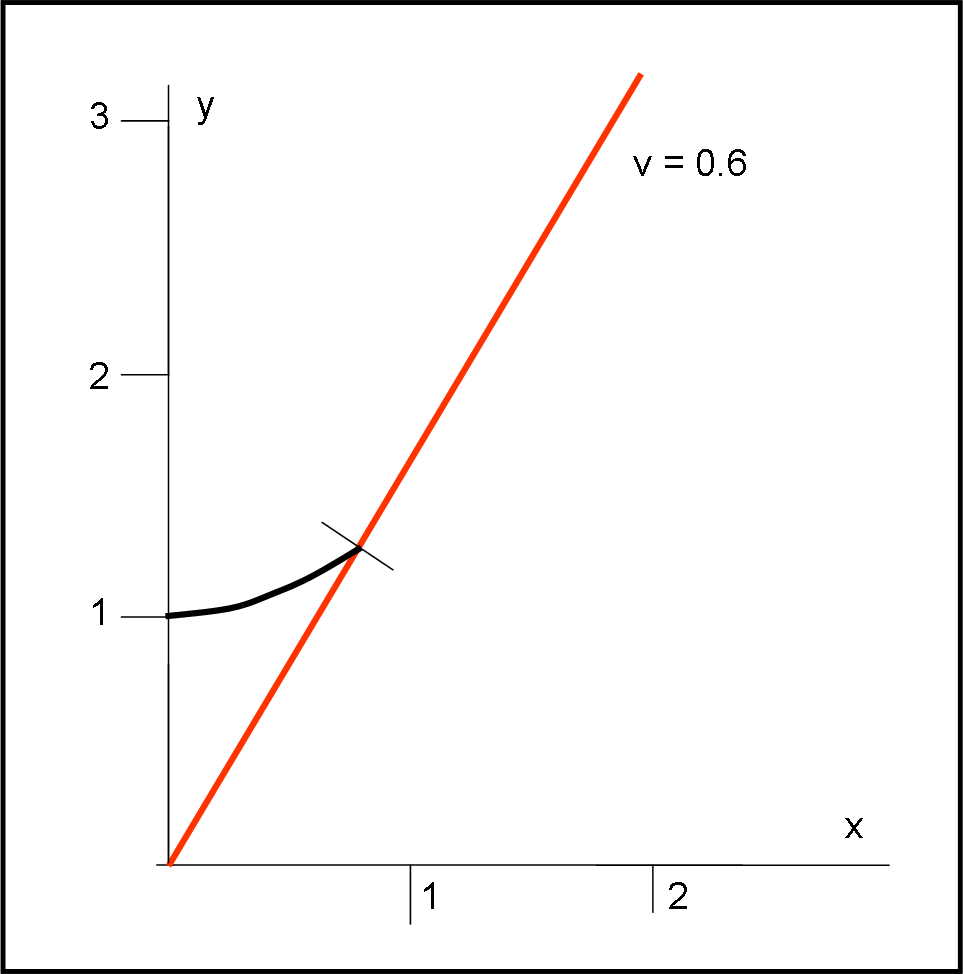
Come sempre, è molto più facile di quello che potrebbe sembrare...
16 commenti
commento per ricevere ... uffa!!!
caro Enzo sembra strano che non riesci a ricevere le notifiche dei commenti sopratutto per il fatto che wordpress ti predispone in automatico in quanto amministratore - autore...
è quello che non riesco a spiegarmi nemmeno io... e anche SMA. Ieri sembrava funzionasse e oggi non più... Per me è la vendetta di Montezuma
Cercherò sempre di prenotare i commenti, ma qualcosa potrebbe sfuggirmi... abbiate pazienza e riprovate se non rispondo...
mah...se mi dite che nell'impostazioni è spuntata l'opzione di notifica...sembra davvero strano..comunque Enzo con i feed rss dei commenti potresti seguire agevolmente le fesserie che diciamo..è un alternativa
Per me è un problema temporaneo di WordPress, visto che funziona ad intermittenza e non abbiamo modificato nulla.
SMA magari l'aggiornamento risolve il problema
carissimi,
posso risolvere facilmente il problema (che speriamo sia solo momentaneo) andando a vedere direttamente nei commenti che sono tutti elencati nel word press... Ci vuole un attimo!
meglio cosi :-)
Caro Enzo, questa volta niente formule, solo disegni.
.. e qualche ragionamento. 
Nelle figure ho aggiunto degli orologi, per mostrare il tempo che misura ogni sistema di riferimento.
Gli orologi rossi si riferiscono al sistema in moto (t'), quelli neri a quello fermo (t), le linee rosse oppure nere in cui i molti orologi segnano lo stesso tempo sono le linee di simultaneità del sistema che osserva.
http://www.astrobin.com/full/34216/M/
Quando è il sistema fermo che osserva, è lui che usa più orologi (neri) per misurare il tempo, mentre il sistema in movimento usa un solo orologio (tempo proprio).
La barra fissa si trova nel sistema in movimento, per cui la luce ci mette 1 secondo del suo tempo (t'=1) per arrivare allo specchio (che corrisponde all'intersezione della curva di calibrazione con l'asse t') ed un altro secondo per tornare all'altra estremità della barra, in totale 2 secondi per andare e tornare.
Per il sistema fermo quando la luce raggiunge lo specchio, secondo i suoi orologi (neri) sono passati 1,25 secondi e quando ritorna all'origine della barra ne sono passati 2,5 di secondi.
Quando è il sistema in movimento che osserva, è lui che usa più orologi (rossi) per misurare il tempo, mentre il sistema fermo usa un solo orologio (tempo proprio).
La barra fissa si trova nel sistema fermo, per cui la luce ci mette 1 secondo del suo tempo (t =1) per arrivare allo specchio ed un altro secondo per tornare all'altra estremità della barra, in totale 2 secondi per andare e tornare (t=2).
Per il sistema in movimento quando la luce raggiunge lo specchio, secondo i suoi orologi (rossi) sono passati 1,25 secondi e quando ritorna all'origine della barra sono passati 2,5 secondi.
Una perfetta simmetria!
Potrei fermarmi qui, ma se il ragionamento è corretto deve essere soddisfatta la condizione che la velocità della luce rimane invariata per qualunque sistema (fermo o in movimento che sia).
In termini grafici significa che le rette che rappresentano la luce devono risultare inclinate di 45° qualunque sia il sistema scelto per rappresentare ciò che accade.
Per rappresentare l'evento, ho usato le due figure precedenti, a cui ho aggiunto l'asse x' e la sua curva di calibrazione, il fascio di luce rappresentato da rette gialle, una lampadina, uno specchio, un rilevatore (rappresentato con l'esplosione), e naturalmente una barra fissa (per il proprio sistema di riferimento).
http://www.astrobin.com/full/34216/N/
Vista dal sistema fermo:
L'evento da osservare si trova nel sistema in movimento, per cui la lunghezza della barra è stata misurata lungo il suo asse dello spazio, ossia X' =1 (intersezione tra curva di calibrazione ed asse X') e tale barra si deve muovere in solido con il sistema in movimento, per cui si muove nel tempo lungo l'asse t' o sue rette parallele.
Anche in questo caso, la figura mostra che la luce colpisce lo specchio dopo 1 secondo di tempo misurato (con l'orologio rosso) lungo l'asse t' (basta vedere cosa segna l'orologio rosso in prossimità dello specchio, ossia lo stesso tempo t' =1 dell'altra estremità della barra) e torna all'origine dopo 2 secondi (t'=2).
Come prima i molti orologi del sistema fermo segnano 1,25 secondi quando la luce raggiunge lo specchio (ossia quando l'orologio rosso segna t'=1) e 2,5 secondi quando torna all'origine della barra.
Vista dal sistema in movimento:
L'evento da osservare si trova nel sistema fermo, per cui la lunghezza della barra è stata misurata lungo l'asse X (X =1) e tale barra rimane ferma, per cui si muove solo nel tempo lungo l'asse t o sue rette parallele.
Anche in questo caso, la figura mostra che la luce colpisce lo specchio dopo 1 secondo di tempo misurato (con l'orologio nero) lungo l'asse t (basta vedere cosa segna l'orologio nero in prossimità dello specchio) e torna all'origine dopo 2 secondi (t=2).
Come prima i molti orologi del sistema in movimento (rossi) segnano 1,25 secondi quando la luce raggiunge lo specchio (orologio nero che segna t=1) e 2,5 secondi quando torna all'origine della barra.
Affinché la velocità della luce rimanga uguale, vista da un sistema esterno (non importa quale dei due) oltre a dilatarsi il tempo devono anche contrarsi le lunghezze.
Nella figura precedente ho anche disegnato un segmento blu (sbiadito) che mostra che anche per il sistema in movimento la lunghezza della barra del sistema fisso (X=1) si contrae, ossia misurata sul suo asse X' è minore di 1.
Sembrerebbe funzionare.......
Paolo
diciamoci la verità... per te era uno scherzo!
Ripeto se qualcuno ha dubbi in proposito ce lo faccia sapere subito!!!!
scusa Paolo,
ma mi era sfuggita la parte finale... Forse non ho capito bene, ma per mantenere la velocità della luce se cresce il tempo deve anche crescere lo spazio percorso. Le contrazioni delle lunghezze sono quasi inutili...
Se calcoli lo spazio percorso nei due casi (visti dal sistema esterno all'esperimento) vedrai che la lunghezza totale percorsa è anche lei 2.5 (in un caso prima due e poi 0.5 e poi il viceversa). Ne segue che la velocità è data da 2.5/2.5 0 1 sempre.
A volte wordpress ci mostra direttamente a video l’errore, altre volte invece ci mostra una pagina bianca, come possiamo capire l’errore in questo caso?
Forse non tutti sanno che wordpress genera un suo Error-Log. Ma un attimo… Che cos’é un error log? Semplicemente non é altro che un file dove vengono registrati tutti gli errori che il nostro wordpress incontra durante il suo funzionamento!
Avete capito bene, in questo file vengono registrati nel dettaglio tutti gli errori del nostro sistema WordPress. Per scaricare il file dovete accedere al vostro FTP e recarvi nella cartella wp-includes, li troverete il vostro file “error_log”.
Una volta aperto il file vi mostrerà rigo per rigo:
[data - ora] errore (file dove risiede l'errore)
In questo modo potrete scovare tutti i problemi del vostro wordpress.
I principali errori di wordpress sono:
1) Error Message:
Cannot modify header information – header already sent
Call to undefined function
Allowed memory size exhausted
2) Un problema con un particolare tema o plugin
3) Errori nei file: WordPress vi segnala in che file e a che riga trovare gli errori (non é sempre preciso, ma recatevi più o meno alla riga indicata e troverete l’errore)
L’errore Cannot modify header information – header already sent per esempio é dato molto spesso dalla presenza di caratteri fuori dai tag, spesso anche un innocuo spazio in più può essere la causa del problema! Questo é l’errore più banale e più difficile da trovare, in quanto spesso si nasconde tra i tag.
Un altro errore molto comune é Call to undefined function, questo problema sta a significare che un plugin o un tema cerca di eseguire una funzione che non trova. Le ragioni di questo errore sono molteplici:
Un errore dovuto ad un aggiornamento automatico di un plugin o un tema (provate a lanciare l’aggiornamento manualmente)
Un errore dovuto ad una auto installazione di un plugin o un tema(rilanciate l’installazione di wordpress manualmente)
Un problema relativo alla compatibilità tra un plugin installato e la versione usata di wordpress (generalmente i plugin troppo nuovi o troppo vecchi possono dare problemi, se non riuscite a riprendere il controllo del vostro wordpress, cancellate la cartella del tema o del plugin direttamente dall’FTP)
Ultimo errore é Fatal Error: Allowed Memory size exhausted, questo errore sta a significare che il vostro WordPress non riesce ad eseguire tutte le sue operazioni perchè ha bisogno di più memoria. La via più veloce per tentare una soluzione al problema é modificare il vostro wp-config.php, il file di configurazione di wordpress aggiungendo la seguente riga:
define('MEMORY_LIMIT', '128M');
La butto li per me scarsa memoria???
Oppure davvero Montezuma il vecchio ci ha preso di mira
Caro Enzo, hai ragione questa frase è fuorviante
: “Affinché la velocità della luce rimanga uguale, vista da un sistema esterno (non importa quale dei due) oltre a dilatarsi il tempo devono anche contrarsi le lunghezze”
Presa alla lettera (come in genere si fa quando si legge qualcosa
) non ha senso, ossia se in in tempo t di 1,25 secondi si percorre uno spazio x inferiore a 1 e più precisamente di 0,8 (il valore esatto di X equivalente ad X'=1 è di 0,8, ossia 1/γ= √(1-β²) = √(1-0,6²) =0,8), la velocità della luce così calcolata (x/t) sarebbe diversa da 1.
Io mi riferivo invece ad una questione puramente grafica, ossia per costruire l'ultima figura vista dal sistema fermo, il segmento solidale con i sistema in movimento ha una certa inclinazione rispetto all'asse X (ossia si trova sull'asse X'), per cui l'estremità del segmento dove è posizionato lo specchio si trova nella posizione giusta per riflettere la luce (t'=1) affinché torni all'origine nel tempo t'=2 (che, visto dal sistema fermo, equivale a t=2,5).
Ciò consente di rappresentare la luce come una retta inclinata di 45° (x/t = 1), che giunge allo specchio quando questo si trova nella corretta posizione spaziotemporale.
Dato che proprio questa inclinazione, insieme al fatto che il segmento deve muoversi lungo l'asse t', genera anche l'apparente contrazione della lunghezza ho cercato di mostrare anche questo aspetto nel grafico.
Concludendo, la frase è malposta e fuorviante ed andrebbe così riscritta:
“La velocità della luce rimane uguale qualunque sia il sistema di riferimento usato per descrivere gli eventi, ma visto da un sistema esterno il tempo si dilata e la lunghezza si contrae”.
Nella soluzione che hai postato la costanza della velocità della luce per entrambi i sistemi è stata ampiamente dimostrata, come era logico aspettarsi (luce descritta con rette a 45°), ossia, ponendo c=1:
x/t = 1
x'/t' = 1
Paolo
caro Paolo,
Ormai so benissimo quali siano le tue capacità interpretative (se sempre l'unico a rispondere 
), ma , appunto per quello, volevo che fossi tu stesso a correggere il tiro per i meno esperti... Speriamo che, a parte le risposte, molti si siano cimentati con il disegnino...
avevo capito che non era un vero errore, ma solo una constatazione che non era inserita al posto giusto...