28/01/16

Quiz: un urto papalliano **

Categorie: Fisica classica Tags: cinematica elementare matematica percorso quiz velocità Scritto da: Vincenzo Zappalà Commenti:50

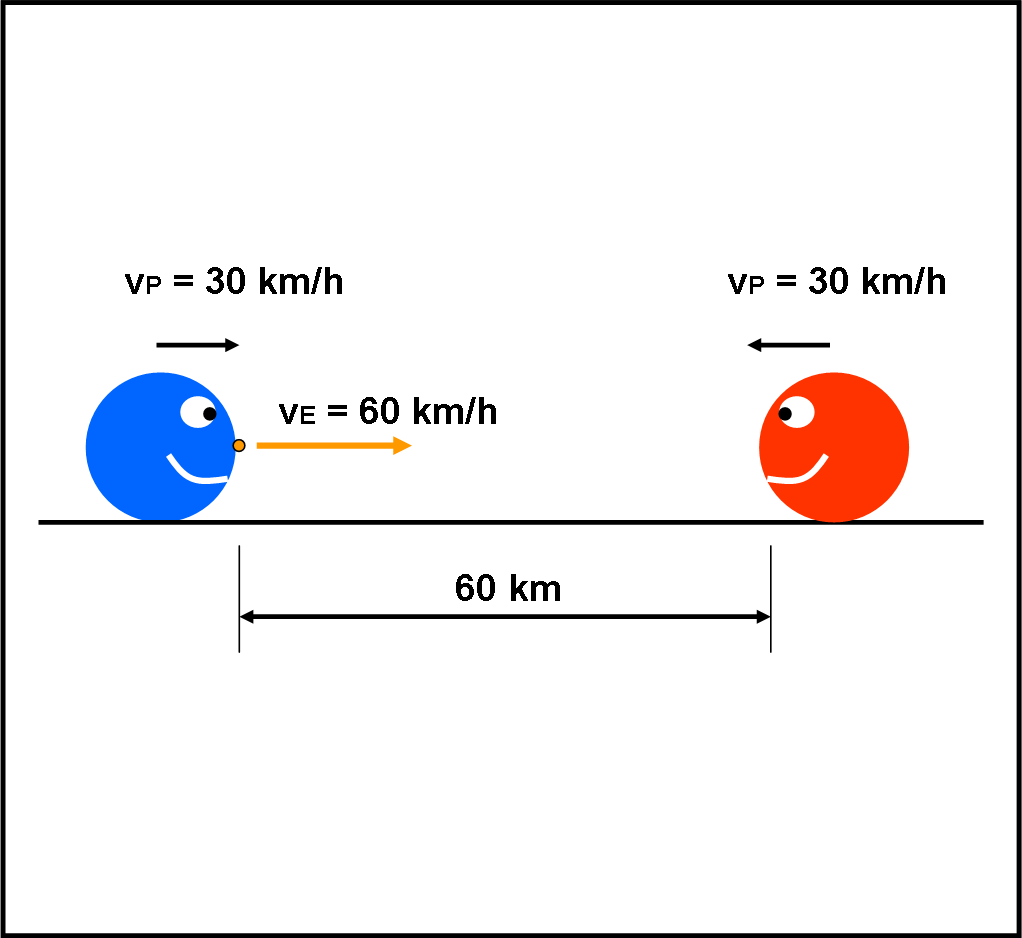
Il gioco è molto semplice e vede due papalatleti che si fronteggiano e che corrono uno verso l’altro, lungo la stessa linea retta, con la stessa velocità v. Sulla fronte di uno di loro viene posto un papalelettrone di dimensioni praticamente nulle. Appena dato il via, i papalatleti si mettono subito in moto con la loro velocità costante, ma il papalelettrone viaggia molto più veloce di loro e, partito dal primo, raggiunge rapidamente il secondo papalatleta. Appena raggiunto, inverte immediatamente la sua corsa e si dirige di nuovo verso il primo papalatleta. Lo raggiunge e inverte nuovamente il suo moto e via dicendo. Un gioco divertentissimo, che dà luogo a un semplice quiz, una volta che si siano impostate le velocità dei papalatleti, la distanza tra di loro e la velocità del papalelettrone.

Ed è proprio quello che vogliamo fare noi. Stabiliamo che la distanza tra i due papalatleti, all’inizio, sia di 60 km. Scegliamo come loro velocità 30 km/ora, mentre quella del papalelettrone è di 60 km/ora. La domanda è veramente semplice: “Quanti viaggi riesce a fare l’elettrone tra un papallo e l’altro prima che i due papalli si scontrino?”.

Sono sicuro che i papallicoli utilizzeranno questo gioco per raccontarci qualche bella storia papalliana, anche perché potrebbe servire per introdurre concetti di più ampia portata.

A me basta la risposta numerica, con la descrizione dei calcoli eseguiti. Tuttavia, chi volesse cercare di impostare un grafico generale con la descrizione del gioco e fare un po’ di conti, vedrebbe che la faccenda si può facilmente “complicare”, alla ricerca di termini ricorrenti, di serie e cose del genere. Per adesso, comunque, limitiamoci al quiz puro e semplice. Poi si vedrà…

Questa volta prometto che non dirò niente per parecchi giorni… muto come un pesce!

Mentre noi abbiamo sviscerato il viaggio di un elettrone che rimbalza tra due papalli, Gatto Gualtiero avrebbe voluto spiegarci come calcolare in un battibaleno quanta strada percorre una mosca che vola avanti e indietro tra due treni... ma aveva troppo sonno e, per questa volta, si è fatto sostituire dalla sua zampa destra Alan che, tuttavia, si è dimostrato all'altezza! Ecco QUI il loro video.

QUI troverete una prima risposta semplice e discorsiva

QUI, invece, una risposta più tecnica che utilizza matematica e geometria

QUI la risposta dei PapalCuriosoni, che si spinge ancora più in là delle precedenti, con un’animazione finale da non perdere

50 commenti

umberto

28/01/2016 at 20:54

scusa ma ho un dubbio sulla velocità dell'elettrone (60 km/h) rispetto a quella dei papalli (30 km/h) non so se sbaglio ma così non può fare tanti giri avanti e indietro
Daniela

28/01/2016 at 22:04

Ciao Zappi,

nonostante le apparenze, sono Valentina e sono stata reclutata per risolvere il quiz.

Secondo me è così:

l'equazione del moto rettilineo uniforme è S=So+vt, dove S è lo spazio percorso, So è lo spazio iniziale, v è la velocità e t è il tempo trascorso. Conosciamo la posizione iniziale di tutti e tre i corpi, ma per risolvere il problema ne dobbiamo considerare due alla volta.

Iniziamo considerando il papalelettrone (1) e il papallo rosso (2): So1=0, S02=60km, v1=60km/h, v2=-30km/h. Ponendo a sistema le due equazioni del moto otteniamo

S=0+60t

S=60-30t

quindi S=40 km e t=2/3h, ovvero l'elettrone si scontra per la prima volta col papallo rosso dopo 40 minuti a una distanza dal punto di partenza di 40 km.

A questo punto consideriamo l'elettrone e il papallo blu. Dobbiamo tener presente che il papallo blu in 40 minuti ha percorso 20 km. Impostando le due equazioni del moto otteniamo

S=20+30t

S=40-60t

Quindi t=2/9h (circa 13 min) e S=80/3 km (circa 27 km).

Visto che il papallo blu e il papallo rosso sono a una distanza di 20 km, prima che il papalelettrone possa scontrarsi con il papallo blu, i due papalli si scontrano. Quindi a questo punto devo calcolare il punto di incontro tra i due papalli:

S=20+30t

S=40-30t

quindi S=30 km e t=1/3h (20 min)

In questo momento e in questa posizione si scontrano tutti e tre i corpi.

La risposta è che il papalelettrone riesce a fare due viaggi prima dello scontro.
Vincenzo Zappalà

29/01/2016 at 05:09

ciao Valentina! Una delle celeberrime papalbelve!!!!!! Che piacere sentirti!!!!!!!!!!!!!!!!

Non posso dire altro, però (niente aiuti su Papalla...)....

Idem per Umberto...

Solo un consiglio... provate a mettere in grafico la situazione...
umberto

29/01/2016 at 06:58

hai ragione, qui basta sapere che la velocità dell'elettrone è maggiore delle altre , ma per il calcolo non serve a niente. La prima volta l'elettrone raggiunge il P2 ad un certo tempo, poi si gira e incontra il P1 ad un tempo minore (le velocità in gioco sono sempre le stesse) mentre le distanze si accorciano sempre di più. Tendono a zero in modo lineare ma la loro somma deve dare un numero finito (60KM perchè si incontrano dopo un ora e l'elettrone ha una velocità di 60 KM/h ). Non si può che concludere che il numero dei tratti è infinito e così pure il numero dell'inversioni.
Daniela

29/01/2016 at 06:59

Bene, riferirò...
Paolo

29/01/2016 at 09:53

Qui c’è lo zampino di papalscherzone che sta giocando ad Achille e la tartaruga.

Se si considera Papalelettrone come un punto privo di dimensioni, gli urti non hanno temine, ma l’intervallo di tempo di ogni rimbalzo diventa infinitesimo.

Se si considera papalelettrone come un corpo con una certa dimensione fisica allora i rimbalzi sono un numero finito… per dare un’idea dopo una trentina di rimbalzi, lo spazio che separa i due Papallli è dell’ordine di 10 alla meno 15 Km.

Ovviamente il tempo che impiegano i due Papalli per incontrarsi a S= 30Km è finito, ed è pari a 1 ora… nel frattempo papalelettrone ha speso 30 km per arrivare fino al punto di incontro dei due Papalli e 30 km di rimbalzi..

Facendo i calcoli ne esce una serie…

Se riesco stasera, provo a postare un paio di calcoli che portano in quella direzione.

Paolo
michele

29/01/2016 at 12:53

P1 , P2 ed e si incontreranno contemporaneamente dopo una ora nel punto di mezzo, dopo che P1 e P2 hanno percorso 30 km ed e ne ha percorsi 60. La matematica, non la logica e la fisica, ci dice che il numero dei rimbalzi è infinito, lo spazio percorso tra due rimbalzi successivi si riduce a 1/3 di quello precedente.
Paolo

29/01/2016 at 15:44

Visto che mi sono lanciato in un'ipotesi, non resta che provare a dimostrarla.

Consiglio a chi vuole cimentarsi nel quiz di non leggere questa ipotesi, tutta da dimostrare e verificare (tra l'altro potrebbe pure essere errata la soluzione che sto proponendo).

I due papallli viaggiano alla stessa velocità costante V(p) di 30 km/h e dato che il quiz non considera fortunatamente le conseguenze degli urti sulle quantità di moto (in fin dei conti la massa di papalelettrone rispetto a quella dei papalli è irrisoria), non possono che incontrarsi a metà percorso, ossia dopo aver percorso 30 Km che alla loro velocità impiegano 1 ora esatta.

Nel medesimo tempo, che d'ora in avanti indicherà come T, l'elettrone percorre 60 km alla velocità v(e) di 60 km/h.

T = So/v(e) = 60 km/60 km/h = 1 ora

Papalelettrone usa 30Km per trovarsi nel punto esatto in cui i due papalli si incontrano e altri 30 km in rimbalzi tra i due papalli.

Il problema, però, è vedere come vengono spesi quei 30 km di rimbalzi, ossia quante volte papalelettrone rimbalza tra i due Papalli.

Ogni volta che papalelettrone colpisce uno dei due papalli entrambi devono occupare la stessa posizione spaziale nel medesimo istante.

Parto dall'istante to, descritto in figura:

a) Papalelettrone si trova nella pozione S(e) = 0

b) Papallo Blu si trova nella posizione S(pb) =0

c) Papallo Rosso si trova nella posizione S(pr) = So = 60km

All'istante t1, avviene il primo urto e papalelettrone deve trovarsi nella stessa posizione del papallo Rosso:

S(e) = v(e) t1.

S(pr) = So - v(p) t1 …………. ma v(p) = ½ v(e)

S(pr) = So - ½ v(e)t1

S(e) = S(pr)

v(e) t1 = So - ½ v(e)t1

v(e) t1 + ½ v(e)t1 = So

3/2 v(e) t1 = So

3/2 t1 = So/v(e)……………….. ma So/v(e) = T

3/2 t1 = T

t1 = 2/3 T

In tale frazione del tempo totale, queste sono le posizioni che assumono papalli e papalelettrone:

S(e) = v(e) t1 = (60) 2/3 T = 40 Km

S (pr) = So - ½ v(e)t1 = 60 – ½ 40 km = 60 -20 = 40 km

S (pb) = ½ v(e)t1 = ½ 40 km = 20 km

All'istante t2, avviene il secondo urto e papalelettrone, la cui velocità cambia di segno, deve trovarsi nella stessa posizione del papallo Blu: S(e) = S (pb)

S(e) = v(e) t1 - v(e) t2 = v(e) (t1 - t2)

S (pb) = ½ v(e)t1 + ½ v(e)t2 = ½ v(e) (t1 + t2)

v(e) t1 - v(e) t2 = ½ v(e)t1 + ½ v(e)t2

v(e) t1 - ½ v(e)t1 = ½ v(e)t2 + v(e) t2

v(e) (t1 - ½ t1) = 3/2 v(e)t2

(2/3 - ½ 2/3) T = 3/2 t2

(2/3 - 1/3) T = 3/2 t2

1/3 T = 3/2 t2

t2 = 2/3 (3) = 2/9 T

(t1 –t2) = (2/3 – 2/9) T = (6 – 2)/9 = 4/9 T

(t1 + t2) = (2/3 + 2/9) T = (6 + 2)/9 = 8/9 T

S(e) = v(e) (t1 - t2) = (60) 4/9 T = 26,6666 Km

S (pb) =½ v(e) (t1 + t2) = ½ (60) 8/9 T = 8/18 (60)T = 4/9 T (60) = 26,6666 Km

S (pr) = So - ½ v(e) (t1 + t2) = 60 - 26,6666 = 33,333333 Km

All'istante t3, avviene il terzo urto e papalelettrone, la cui velocità cambia nuovamente di segno, deve trovarsi nella stessa posizione del papallo Rosso:

S(e) = S (pr)

S(e) = v(e) (t1 - t2) + v(e) t3 = 4/9 v(e) T + v(e) t3

S (pr) = So - ½ v(e) (t1 + t2) - v(e) t3 = So - ½ v(e) 8/9 T - ½ v(e) t3 = So - v(e) 8/18 T - ½ v(e) t3

S (pr) = So - 4/9 v(e) T – ½ v(e) t3

4/9 T + v(e) t3 = So - 4/9 v(e) T – ½ v(e) t3

4/9 v(e) T + 4/9 v(e) T = So – ½ v(e) t3 - v(e) t3

8/9 T = So/ v(e) -3/2 v(e)t3/v(e)………………… ma So/v(e) = T

8/9 T = T - 3/2 t3

3/2 t3 = T – 8/9 T

3/2 t3 = T (9-8)/9 = 1/9T

t3 = (1/9) (2/3) T = 2/27 T

(t1 –t2 + t3) = (2/3 – 2/9 + 2/27) T = T (18 – 6 + 2)/27 = 14/27 T

(t1 + t2 + t3) = (2/3 + 2/9 + 2/27) T = T (18 + 6 + 2)/27 = 26/27 T

S(e) = V(e) (t1-t2+t3) = (60) 14/27 T = 31,1111 Km

S (pr) = So - 1/2 v(e) (t1 + t2 + t3) = 60 – ½ 60 (26/27) T = 60 – 30 (26/27) = 60 -28,888 = 31,111 Km

S (pb) = ½ V(e) (t1-t2+t3) = 30 (26/27) T= 28,888 Km

All'istante t4, avviene il quarto urto e papalelettrone, la cui velocità cambia nuovamente di segno, deve trovarsi nella stessa posizione del papallo Blu:

S(e) = S (pb)

S (e) = v(e) (t1-t2+t3) – v(e) t4 = v(e) 14/27 T - v(e) t4

S (pb) = ½ V(e) (t1-t2+t3) + ½ v(e) t4 = ½ v(e) (26/27 T) + ½ v(e) t4

S (pb) = v(e) 13/27 T + ½ v(e) t4

v(e) 14/27 T - v(e) t4 = v(e) 13/27 T + ½ v(e) t4

v(e) 14/27 T - v(e) 13/27 T = v(e) t4 + ½ v(e) t4

v(e) 1/27 T = 3/2 v(e) t4

1/27 T = 3/2 t4

t4 = 2/27 (3) T = 2/81 T

(t1 – t2 + t3 –t4 ) = (2/3 – 2/9 + 2/27 – 2/ 81) T= T (54 – 18 + 6 – 2)/81 = 40/81 T

(t1 + t2 + t3 + t4 ) = (2/3 + 2/9 + 2/27 + 2/ 81) T= T (54 + 18 + 6 + 2)/81 = 80/81 T

S (e) = v(e) (t1-t2+t3 –t4) = (60) 40/81 T = 29,6296 Km

S (pb) = ½ v(e) (t1+ t2+t3 + t4) = ½ (60) 80/81 T = (60) 40/81 T = 29,6296 Km

S (pr) = So - ½ v(e) (t1+ t2+t3 + t4) = So - ½ (60) 80/81 T = 60 - (60) 40/81 T = 60- 29,6296 = 30,3704

Si potrebbe proseguire, ma mi sembra che basti per trovare una serie di intervalli di tempo che sommati fra loro formino il tempo totale T di 1 ora, che occorre a papalli ed a palaelettrone per trovarsi tutti e tre nella stessa posizione nello stesso istante.

Ricapitolando:

t1 = 2/3 T...... t2= 2/9 T..................t3= 2/27 T.......................t4 = 2/81 T

che posso scrivere come:

$t1 = 2/3^{1} T.....t2= 2/3^{2} T.......t3= 2/3^{3}T ......t4= 2/3^{4}T$

Mi basta prendere in considerazione quando il Papallo Blu incontra quello Rosso, per compattare la serie: S(pb) = S(pr) = 30 Km........ T = 1 ora

$S(pb) = 1/2 v(e) \sum_{n=1}^{\infty }2/3^{n}$

o, anche, dato che 1/2 v(e) = v(p)

$S(pb) = v(p) \sum_{n=1}^{\infty }2/3^{n}$

o anche:

$S(pr) = S_{0}- v(p) \sum_{n=1}^{\infty }2/3^{n}$

La serie consente di approssimare il risultato al grado che si vuole.... ma papalelettrone ha una dimensione fisica, per cui oltre un certo grado di approssimazione è inutile andare poichè il povero papalelettrone è schiacciato tra i due papalli e non può più muoversi...

Paolo
umberto

29/01/2016 at 17:00

ribadisco le mia convinzione, anche se non riesco a formalizzarla bene. La domanda del quiz è Quanti viaggi riesce a fare l’elettrone tra un papallo e l’altro prima che i due papalli si scontrino?

non chiede quanto spazio abbia percorso, nè che si debba calcolare un termine generale di una serie, per trovare un risultato che ormai sappiamo tutti che è 60 KM. Il problema è dimostrare che i viaggi sono infiniti.

Sappiamo che la distanza fra i due P1 E P2 diminuisce in modo lineare e va a zero per t1=S0/2Vp

$S_{0}= S_{0}-V_{p}\cdot t$

dovendo essere confinato in questo valore il tratto percorso dall'elettrone, ma diminuendo sempre di più lo spazio, aumentano le inversioni che in un intervallo di tempo può fare l'elettrone. Deve percorre uno spazio sempre più piccolo con la stessa velocità relativa. Man mano che ci avvicina a un $\Delta S=0$ le inversioni tendono a infinito. Si nota anche dalla figura
Paolo

29/01/2016 at 17:09

Il problema a mio avviso è che l'elettrone non si può considerare come un punto, ma ha delle dimensioni fisiche che pongono un limite agli intervalli di spazio percorsi in intervalli infinitesimi di tempo, ossia se non ho sbagliato qualche calcolo, al quarantesimo urto (n =40) lo spazio tra i due papallli dovrebbe essersi ridotto a:

$(4,9) 10^{-15} metri$

il “diametro” di un elettrone dovrebbe essere di

$(5,6) 10^{-15} metri$

GAME OVER !

Poi, magari mi sbaglio, ma è questo il bello dei giochi papalliani... che spesso sbagliando si impara..

Paolo
Vincenzo Zappalà

29/01/2016 at 17:14

faccio fatica a stare zitto... ma l'ho promesso... (sperando che altri si facciano sentire...)
umberto

29/01/2016 at 17:22

mi sembra che il Prof.Vincenzo parlasse di..

papalelettrone di dimensioni praticamente nulle.
Vincenzo Zappalà

29/01/2016 at 17:33

occhio, ragazzi, che state dicendo la stessa cosa
Paolo

29/01/2016 at 17:37

A mio avviso, dal punto di vista matematico, se non si pongono limiti alle dimensioni dell'elettrone, a quelle dello spazio (lunghezza di plack) ed alla minima misura del tempo sono convinto anch'io che i viaggi sono infiniti ... su questo concordo con te.

Se invece si tiene conto di tali limiti "fisici" allora le cose a mio avviso cambiano...

Paolo
umberto

29/01/2016 at 18:20

senz'altro; io l'ho preso come un problema di astrazione puramente matematica. E dire la verità avrei potuto cercare di giustificarlo in altro modo, cercando la distanza in modo ricorsivo e vedendo che non va mai a zero, se non al limite(é una frazione del termine precedente). Con degli esempi numerici ci si riesce ma il caso generale é fuori dalla mia portata.
Vincenzo Zappalà

29/01/2016 at 18:25

non credo proprio Umberto... non avresti sicuramente problemi... ne sono convinto!
umberto

29/01/2016 at 18:32

grazie dell' incoraggiamento, proverò domani mattina se non chiudi il quiz
Vincenzo Zappalà

29/01/2016 at 18:40

no, no, lo lascio aperto...
umberto

30/01/2016 at 07:30

Traviamo i tratti di inversione in successione:

il primo tratto si trova con il sistema:

$\left\{\begin{matrix} S_{1}=S_{0}-V_{p}\cdot t_{1}\\ S_{1}=V_{e}\cdot t_{1} \end{matrix}\right.$

$\left\{\begin{matrix} S_{1}=S_{0}-V_{p}\cdot t_{1}\\ t_{1}=\frac{S_{1}}{V_{e}} \end{matrix}\right.$

$\left\{\begin{matrix} S_{1}=S_{0}-V_{p}\cdot S_{1}/V_{e}\\ t_{1}=\frac{S_{1}}{V_{e}} \end{matrix}\right.$

porto a sinistra il termine con S1, raccolgo e ricavo S1:

$S_{1}=S_{0} V_{e}/(V_{e}+V_{p})$

cerco il secondo tratto in funzione del primo

$\left\{\begin{matrix} S_{2}=S_{1}-V_{p}\cdot t_{1}-V_{p}\cdot t_{2}\\ S_{2}=V_{e}\cdot t_{2} \end{matrix}\right.$

sostituisco a t1, t2 le espressioni in funzione di S1,S2

$S_{2}=S_{1}-V_{p}\cdot S_{1}/V_{e}-V_{p}\cdot S_{2}/V_{e}$

porto a primo membro S2, raccolgo S1, S2:

$S_{2}(1+V_{p}/V_{e})=S_{1}(V_{e}-V_{p})/V_{e}$

sostituisco a S1 la sua espressione tramite S0

$S_{1}=S_{0} V_{e}/V_{e}+V_{p}$

e ottengo:

$S_{2}=S_{0}\cdot \frac{V_{e}}{V_{e} + V_{p}}\cdot \frac{V_{e}-V_{p}}{V_{e} + V_{p}}$

non raccolgo il prodotto sotto in un unico quadrato per la ragione che vedremo

Calcolo S3 inFunzione di S2:

$S_{3}=S_{2}-V_{p}\cdot t_{2}-V_{p}\cdot t_{3}\$

facendo gli stessi conti sostituendo t2 e t3 con le espressioni S2/Ve e S3/Ve

$S_{3}(1+V_{p}/V_{e})=S_{2}(V_{e}-V_{p})/V_{e}$

Sostituendo l'espressione che abbiamo ricavato per S2: $S_{3}=S_{0}\cdot \frac{V_{e}}{V_{e} + V_{p}}\cdot \frac{(V_{e}-V_{p})^{2}}{(V_{e} + V_{p})^{2}}$

confrontando S0,S1,S2 sembra che:

$S_{n}=S_{0}\cdot \frac{V_{e}}{V_{e} + V_{p}}\cdot \frac{(V_{e}-V_{p})^{n-1}}{(V_{e} + V_{p})^{n-1}}$

Quindi qualsiasi sia n troviamo sempre una soluzione per il sistema generico,

anche se il la distanza percorsa diventa sempre più piccola, quindi n il numero dei trattini (come quello delle inversioni) è infinito. La somma dei trattini è quella

di una serie geometrica con ragione minore di 1,quindi convergente.

Spero non ci siano i soliti errori dovuti al copia incolla con Latex.
michele

30/01/2016 at 08:19

Sinteticamente, non ci saranno più rimbalzi quando la distanza tra P1 e P2 si annulla.

Distanza iniziale S0.

Al primo rimbalzo P1 e P2 hanno percorso ciascuna S0/3, l'elettrone 2S0/3, P1 e P2 distano tra loro S0/3.

Al secondo rimbalzo la distanza tra P1 e P2 si è ridotta a S0/3^2

All'ennesimo rimbalzo la distanza diventa S0/3^n.

Essa si annulla per n che va all'infinito.
Vincenzo Zappalà

30/01/2016 at 08:39

caro Umberto,

potresti fare una figura con la varie grandezze? Non mi torna qualcosa nella formula che segue la frase "cerco il secondo tratto in funzione del primo"... Soprattutto la prima relazione del sistema...

Può darsi che sia io a non capire bene la figura...

Grazie!
Vincenzo Zappalà

30/01/2016 at 08:59

Caro Umberto,

penso di aver capito cosa hai fatto... Sarebbe meglio comunque far vedere la figura, dato che stai spostando gli assi cartesiani di volta in volta... (sempre che abbia capito bene...)
Vincenzo Zappalà

30/01/2016 at 10:05

caro Umberto, ho capito il tuo approccio... Però, secondo me, sarebbe bene veramente fare vedere la figura per renderla più chiara a tutti... Io l'ho ricavata in un certo modo, ma mi piacerebbe sapere se tu hai fatto lo stesso. La matematica è un linguaggio, ma si possono usare parole diverse per raccontare la stessa storia...
umberto

30/01/2016 at 11:49

scusa sono fuori casa cercherò di fare quella figura al più presto
Vincenzo Zappalà

30/01/2016 at 14:40

non preoccuparti... abbiamo tempo
Alvermag

30/01/2016 at 18:38

Allora, vediamo.
Ho disegnato nel diagramma cartesiano S-T i percorsi dei tre protagonisti.
Osservo i moti da un sistema esterno al trio, quindi fermo rispetto ad essi.
La traiettoria spazio-temporale di P1 è un segmento obliquo la cui pendenza rappresenta la velocità di 30 km/h.
La traiettoria spazio-temporale di P2 è un segmento obliquo la cui pendenza rappresenta la velocità di 30 km/h. P2 si muove però in direzione opposta a P1.
La traiettoria spazio-temporale di E è un segmento obliquo la cui pendenza rappresenta la velocità di 90 km/h. E si muove da P1 verso P2.
Mi pare che il gioco stia nel trasferimento di quantità di moto che si verifica ad ogni urto.

Nel primo tratto (E diretto da P1 verso P2) la velocità di E, osservato dall’esterno, vale 90 km/h. Ai 60 km/h propri bisogna infatti sommare i 30 km/h forniti da P1.

Dopo il primo urto con P2 la velocità di E diventa pari a 60 km/h, perché bisogna sottrarre i 30 km/h di P2 che sopraggiunge in senso opposto.

Dopo il successivo urto con P1 la velocità di E diventa pari a 30 km/h, perché bisogna ancora sottrarre i 30 km/h di P1 che sopraggiunge in senso opposto.
A questo punto E viaggia di conserva con P1 fino ad incontrare, insieme a P1, P2 ponendo quindi fine alla carambola.

I calcoli matematici mi rendono:
T1 = 0,50h ; SE = 45 km
T2 = 0,33h ; SE = 20 km
T3 = 0,16h ; SE = 5 km

L’elettrottero (elettrone-papallottero) ha percorso 70 km.

Il tempo complessivo è pari ad 1h.

N.B.: nel trasferimento del moto ho considerato la massa dell'elettrottero insignificante rispetto a quella dei due papallotteri.

Non mi chiedere di mandarti la figura perchè non so come fare ....

comunque è un triangolo con all'interno le tre triettorie di E. L'ultimo tratto (percorso nel tempo T3) coincide con il percorso di P1.

Boh, mi sembra ragionevole .....
Vincenzo Zappalà

30/01/2016 at 18:58

caro Alvy,

innanzitutto la velocità dell'elettrone è di 60 km/h. Non riceve nessuna spinta dal papallo: lui viaggia in modo indipendente. Ma, soprattutto, non vi è trasferimento di quantità di moto (è molto più semplice). L'elettrone raggiunge il secondo papallo e torna indietro con la sua velocità senza urto (comunque la conservazione darebbe qualcosa di diverso, mi sembra...). E' un po' come se l'elettrone vivesse in modo indipendente, come un uccellino che va e viene senza toccare realmente i papalli.

Probabilmente non mi sono spiegato bene, ma la cosa è molto più semplice ed è di pura cinematica.

Il problema è veramente elementare...
Vincenzo Zappalà

30/01/2016 at 19:01

Ah... l'urto del titolo, si riferisce al momento in cui i due papalli si scontrano...e non a quello dell'elettrone con loro... Attenzione, comunque, a mettere una massa uguale a zero... se noricadiamo nel fotone e nella sua quantità di moto (ma lui viaggi un po' più veloce...).
Alvermag

30/01/2016 at 21:38

Si, effettivamente impostando i calcoli la conservazione della quantità di moto e dell'energia cinetica danno risultati diversi da quelli che ho supposto intuitivamente.

Bene, niente urti allora.
Fabio

01/02/2016 at 21:52

Durante gli studi di fisica devo essermi perso qualcosa, perché non ho mai sentito parlare di papalla e papallicoli. Cosa è una nuova teoria della materia? Sarei curioso di conoscerla, illustre collega!
Paolo De Lorenzo

01/02/2016 at 21:56

Io lo so di cosa si tratta, è la nuova teoria gravitazionale che serve a far atterrare le sonde in modo perfetto sulla superficie di una cometa. All'INAF non la conoscono ancora, giusto?!
Vincenzo Zappalà

02/02/2016 at 05:58

Caro Fabio,

tu probabilmente sei troppo giovane e non ti ricordi che molti anni fa, prima dell'avvento della materia e dell'energia oscura, che hanno risolto tutto e di più, si parlava molto di Papalla e della fisica papalliana. Pensa che ne parlavano perfino a Carosello... Poi, come al solito, l'uomo ha preferito non accettare qualcuno che ne sapesse più di lui e ha preferito cancellare Papalla dai libri di fisica (si dice che perfino Einstein abbia scopiazzato la relatività papalliana ... per non parlare di Heisenberg). La materia oscura e sua sorella energia sono molto più comode, dato che si possono costruire tutte le teorie possibili, senza che le osservazioni possano rompere le scatole. I papalliani, invece, pur essendo molto giocherelloni, sono anche terribilmente rigorosi...

Ti devo confidare che temiamo molto un'azione di censura, prima o poi...
Vincenzo Zappalà

02/02/2016 at 06:00

caro Paolo,

per favore... non dire niente! Non vorremmo che partisse un terribile gioco di spionaggio internazionale. Ne abbiamo già abbastanza di guerre più o meno costruite "ad hoc"...
Fabrizio

02/02/2016 at 10:32

Arrivo solo ora a dire la mia che non porta ad un risultato diverso da quello già raggiunto.

Chiamo $d_0$ la distanza iniziale tra il papallo rosso e il papallo blu.

Al momento dell'incontro tra i due papalli, ciascuno di loro avrà percorso un distanza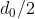 $d_0/2$ . A quel momento, l'elettrone (E) dovrà avere percorso una distanza pari a 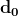$\mathit{\mathbf{d_0}}$ , viaggiando a velocità doppia dei papalli. In grassetto perchè serve nel seguito del ragionamente.

Quale è la distanza che percorre (E) tra due incontri successivi?

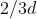Se $d$ è la distanza alla partenza, viaggiando (E) a velocità doppia del papallo che gli viene incontro, la distanza percorsa da (E) è doppia di quella del papallo, quindi al momento dell'incontro (E) avrà percorso $2/3 d$ ed il papallo avra percorso $1/3 d$ .

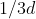Poichè anche l'altro papallo avrà percorso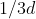 $1/3 d$ , la distanza tra i due papalli sarà diventata $1/3 d$ .

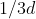In sintesi:

Incontro    Distanza percorsa da (E)     Distanza tra i papalli

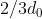
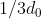
1                          $2/3 d_0$                                           $1/3 d_0$

2               $2/3 d_1= 2/3 (1/3 d_0)$                          $(1/3)^{2}d_0$

i         $2/3 d_i_-_1=2/3 (1/3)^{^{i-1}}d_0$                      $(1/3)^{i}d_0$

Quindi ad un certo incontro N_esimo, (E) avra percorso in totale

$\sum_{i=1}^{N}2/3 (1/3)^{^{i-1}}d_0=2/3 d_0 \sum_{i=0}^{N-1} (1/3)^{^{i}}$

che al momento dell'incontro a tre deve essere uguale a $d_0$ , come visto sopra. Quindi N deve essere tale che:

$\sum_{i=0}^{N-1} (1/3)^{^{i}}=3/2$

Poichè questa somma di serie geometrica ha come valore limite proprio 3/2, sembrerebbe che N non possa essere finito, almeno nello scenario ideale del quiz.
Fabrizio

02/02/2016 at 13:43

Lo stesso ragionamento può essere fatto per la distanza percorsa dai Papalli. I Papalli percorrono tra ogni incontro di uno di essi con (E) 1/3 della distanza residua. Anche la distanza residua si riduce ogni incontro di un fattore 1/3. La coincidenza deriva dalla scelta del rapporto tra le velocità.

La distanza percorsa da ciascuno dei Papalli al momento del N-esimo incontro è quindi:

$\sum_{i=1}^{N}(1/3)^{i}d_0$

che al momento dell'incontro a tre deve essere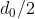 $d_0/2$ , cioé

$\sum_{i=1}^{N}(1/3)^{i}=1/2$

che coincide con il valore limite della somma di questa serie geometrica.

Quindi N sembra non poter essere finito.
Fabrizio

02/02/2016 at 14:36

Scusate, ma continuo a pensare al quiz perchè le soluzioni trovate mi sembrano troppo complicate.

Forse è più semplice.

Sappiamo dalle equazione del moto dei Papalli che essi si troveranno nello stesso punto all'istante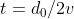 $t=d_0/2v$ e che quindi a quell'istante sarà con loro anche l'elettrone.

Supponiamo che il numero dei percorsi fatti dall'elettrone sia finito e l'ultimo incontro tra E ed uno dei Papalli (diciamo il Rosso) sia avvenuto a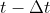 $t-\Delta t$ ad una distanza 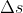$\Delta s$ dal punto di incontro con l'altro Papallo. Per incontrarsi con il Papallo Blu, sia E che il Pappallo Rosso dobrebbero avere fatto il percorso 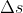$\Delta s$ in un tempo 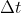$\Delta t$ , cioè essere andati alla stessa velocità, ma ciò contradice l'ipotesi che la velocità di E sia doppia di quella dei Papalli.

Quindi non può esistere questo ultimo percorso, cioè il numero dei percorsi fatti da E non può essere finito.
Vincenzo Zappalà

02/02/2016 at 14:55

caro Fabrizio,

io consiglierei di esprimere come serie l'intervallo di tempo tra due incontri. Questa è una progressione geometrica con n che deve andare a infinito per ottenere il valore finale del tempo. Puoi ragionare in termini generici e non di caso particolare... E' quello che faremo tra non molto...
Alvermag

02/02/2016 at 17:01

... e pensare che stavo diventando matto nel cercare una soluzione diversa da quella effettiva. Comunque impostassi il ragionamento trovavo una serie infinita di rimbalzi ma, non contento, mi sono ingegnato a cercare soluzioni improbabili pur di trasformare l'infinito in finito!

... mi pare che qualcun altro non abbia prestato fede a certe sue conclusioni "correggendole" tramite il ricorso ad una .... costante ..... mah, forse mi attende il nobel .....
Vincenzo Zappalà

02/02/2016 at 17:34

caro Alvy,

il Nobel non l'ha avuto per quello, ma per la soluzione di un urto un po' speciale...
Vincenzo Zappalà

02/02/2016 at 17:34

Oh... Alvy... ti voglio pimpante per la dinamica relativistica!!! Mi raccomando...
Fabrizio

02/02/2016 at 19:00
Provo a seguire il suggerimento del professore generalizzando e considerando il tempo tra gli incontri.

Mi sembra che la dimostrazione per assurdo che ho tentato prima, se valida, sia comunque più esplicativa della ragione degli infiniti rimbalzi dell'elettrone.

Indico con $d_0$ la distanza iniziale tra i Papalli, con v la velocità dei Papalli e con k*v la velocità dell'elettrone (E), assumendo k>1.

Il primo punto di incontro tra elettrone e Papallo Blu (B) dovrà essere tale che la distanza percorsa da E sia k volte la distanza percorsa da B e che la loro somma sia $d_0$ .

Quindi la distanza percorsa dal Papallo Blu sarà: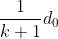 $\frac{1}{k+1}d_0$

di conseguenza il tempo trascorso sarà: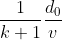 $\frac{1}{k+1}\frac{d_0}{v}$

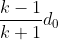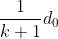La distanza tra i due Papalli si sarà ridotta a $\frac{k-1}{k+1}d_0$ , avendo anche l'altro papallo percorso $\frac{1}{k+1}d_0$ .

Poichè questo vale per ogni incontro elettrone-Papallo si può dire che:

la distanza residua tra Papalli al i-esimo incontro è

$\left (\frac{k-1}{k+1} \right )^{i}d_0$

l'intervallo di tempo trascorso dall'ultimo incontro è

$\frac{1}{k+1}\frac{d{_{i-1}}}{v}=\frac{1}{k+1}\left (\frac{k-1}{k+1} \right )^{i-1}\frac{d{_{0}}}{v}$

Quindi il tempo totale trascorso al momento dell'n-esimo incontro sarà la somma degli intervalli tra incontri:

$\sum_{i=1}^{n}\frac{1}{k+1}\left (\frac{k-1}{k+1} \right )^{i-1}\frac{d{_{0}}}{v}$

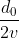Sappiamo che al momento dell'incontro dei due Papalli ciascuno dei Papalli avrà percorso una distanza $\frac{d_0}{2}$ e che sarà quindi trascorso un tempo $\frac{d_0}{2v}$ .

Se vogliamo che l'incontro N-esimo sia quello finale dovra essere

$\sum_{i=1}^{n}\frac{1}{k+1}\left (\frac{k-1}{k+1} \right )^{i-1}\frac{d_0}{v}=\frac{d_0}{2v}$ che isolando la somma e semplificando diventa $\sum_{i=1}^{n}\left (\frac{k-1}{k+1} \right )^{i-1}=\sum_{j=0}^{n-1}\left (\frac{k-1}{k+1} \right )^{j}=\frac{k+1}{2}$

Il valore limite della somma della serie è prorio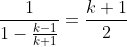 $\frac{1}{1-\frac{k-1}{k+1}}=\frac{k+1}{2}$

Quindi n non può essere finito.
Alvermag

02/02/2016 at 19:59

Eh caro Enzo, sto tentando di recuperare il tempo perduto.

Ho ricominciato a leggere - con estrema attenzione - la RR di Minkowski.

Sai, è un pò come la Recherche di Marcel Proust: ad ogni nuova lettura si trovano spunti diversi e nuovi aspetti da puntualizzare.

Mi accorgo solo ora di aver involontariamente introdotto la Recherche già nella prima riga di questo messaggio ... curioso! Mah, probabilmente quell'opera immortale deve essermi entrata nell'anima....
Vincenzo Zappalà

03/02/2016 at 04:50

caro Fabrizio,

hai pienamente ragione... il problemino può essere risolto e dimostrato in tanti modi diversi. Qualcuno verrà esposto nel prossimo articolo, ma se ne possono trovare molti altri. In poche parole è una specie di "scioglilingua" matematico, utilissimo per padroneggiare il linguaggio... matematico, appunto!
Fabrizio

03/02/2016 at 07:48

Caro professore,

hai perfettamente ragione tu. Infatti mi è stato utilissimo per ritrovare alcuni modi di manipolare la somme di serie ormai sepolti in qualche angolo della memoria, oltre che esercitere la CPU, che non fa mai male.
Vincenzo Zappalà

03/02/2016 at 08:01

Hai capito perfettamente le motivazioni, caro Fabrizio: la matematica merita di essere ogni tanto sponsorizzata!!! !
Arturo Lorenzo

15/03/2016 at 12:09

Ho letto solo oggi questo quiz, e le risposte.

Aggiungo solo che personalmente ho semplificato un pò il problema assumendo che il papallo sia no solo, quello da cui parte l'elettrone, quindi il blu, e che si muova, lui e l'elettrone, con velocità pari a 30+30 e 30+60 km/h rispettivamente. L'elettrone, quindi, anzichè urtare l'altro papallo in movimento è come se urtasse il papallo rosso fermo ma muovendosi con velocità di 90 km/h.

Fatto questo, ho costruito il grafico delle leggi orarie del papallo blu e dell'elettrone nel piano s, t (spazio sull'asse delle ordinate e tempo sull'asse delle ascisse). In particolare , ho una retta rp passante per l'origine e inclinata di vp (60 km/h) rispetto all'asse dei tempi per il papallo, e una retta re1 inclinata di ve (90 km/h) per l'elettrone. La retta rp incontra quella orizzontale y=60km in corrispondenza del punto con ascissa t=1 h. La retta re1, invece, incontra la stessa retta orizzontale in corrispondenza del punto con ascissa t = 60/90 h. Poichè l'elettrone dopo l'urto torna indietro verso il papallo blu, dal suddetto punto passa la retta re2 relativa alla legge oraria dell'elettrone dopo il primo urto, quindi inclinata stavolta di -90km/h rispetto all'asse dei tempi. Tale retta andrà ad incontrare la rp in un certo punto di cui trovo le coordinate mettendo a sistema l'equazione della retta rp e quella della retta re2. Reitero il procedimento n volte , ottenendo n urti tra l'elettrone e il papallo blu. I grafici li ho ottenuto utilizzando l'applicazione online desmos, per cui potete vederli qui:

https://www.desmos.com/calculator/7to1idpall

Dimenticavo di precisare che ho amplificato l'asse dei tempi di 60 volte per avere una maggiore leggibilità dei grafici e in tal modo, inoltre, le due coordinate dei vari punti di interesenzione tra le rette coincidono. Mi dovrò ricordare , per ottenere il valore reale dei tempi, di dividere il valore letto sul grafico per 60.

Mi sono poi preso la briga di calcolare analiticamente l'espressione istante di tempo relativo ai primi 5 urti urto dell'elettrone sul papallo blu, accorgendomi che alla fine posso generalizzare e calcolare il suo valore anche per un generico urto n-esimo attraverso la seguente espressione:

$t_{2n}=\frac{150*5^{n-1}-90+90t_{1}}{150*5^{n-1}}$

dove n = n-esimo urto tra elettrone e papallo blu

t1 = stante di tempo in cui l'elettrone raggiunge il papallo rosso = 60/90 s

Effettivamente, se avessimo una precisione di misura infinita, avremmo infiniti urtri tra elettrone e papallo blu. Nella realtà, il numero degli urti sarebbe quello oltre il quale non saremmo più in grado di misurare le distanze :-)
Arturo Lorenzo

15/03/2016 at 13:00

Dimenticavo: ho letto tutte le risposte e le soluzioni al quiz. Davvero esaurienti e complete. Prendete quindi la mia risposta come quella di chi voleva solo dire la sua su questo intrigante quiz, scoperto in ritardo. E' stato già spiegato tutto e bene. :-)
PapalScherzone

15/03/2016 at 13:12

Grazie Arturo!

In questo Circolo non siamo perfetti, ma ci si impegna affinché ogni lettore abbia la possibilità di comprendere ciò che viene proposto!

Posso darti un consiglio da amico? Nel caso tu non lo abbia già fatto, prova a leggere anche i tre articoli i cui link compaiono in calce a questo... troverai lo stesso quiz spiegato in modi diversi per andare incontro a livelli di comprensione diversi.
Arturo Lorenzo

15/03/2016 at 14:58

Certo, Papalscherzone, già letti, ma dopo la mia prima risposta (non me ne ero accorto prima, avevo letto solo le risposte al quiz ma non le spiegazioni contenute nei tre articoli). I tre articoli meritano di essere letti e apprezzati anche per la grafica.
PapalScherzone

15/03/2016 at 15:01

Bene! Ti ringrazio a nome degli autori!!