Categorie: Fisica Fisica classica Fisica di Papalla Matematica Matematica di Papalla
Tags: Papalcuriosoni
Scritto da: I Papallicoli
Commenti:18
I papalcuriosoni alle prese con il Quiz sul Papalurto
Abbiamo visto il vostro quiz sul papalurto.... grazie per lo spunto, qui su Papalla siamo sempre in cerca di nuovi giochi.

Sul pianeta Papalla, quando nascono nuovi giochi, immediatamente entra in azione la squadra dei Papalcuriosoni.
Si, proprio loro, quelli che compaiono gridando: “STOP AL PANICO”!
I Papalcuriosoni amano smontare e rimontare ogni gioco per comprenderne il funzionamento.
Perciò abbiamo sottoposto a loro il vostro gioco-quiz sul papalurto, che trovate QUI.
I papalli, come al solito, quando c'è da giocare non si tirano mai indietro e due PapalAtleti e un amico papalelettrone sono pronti a darci una mano in questa giocosa rappresentazione.
I Papalcursioni, però, non intendono limitarsi a rispondere al quiz, loro nel rimontaggio del gioco vorrebbero trovare qualcosa che sia applicabile anche ad altri giochi simili, con velocità e distanze diverse da quelle indicate nel quiz.
Un'impresa non facile che merita di essere seguita passo dopo passo.
Innanzitutto Papalmatematico consiglia di usare delle definizioni sintetiche per indicare tempi, distanze e velocità:
d0 = distanza iniziale tra i due PapalAtleti (nel quiz 60 km)
vp = velocità di ogni PapalAtleta (nel quiz 30 km/h)
ve = velocità di papalelettrone (nel quiz 60 km/h)
t0 = tempo iniziale
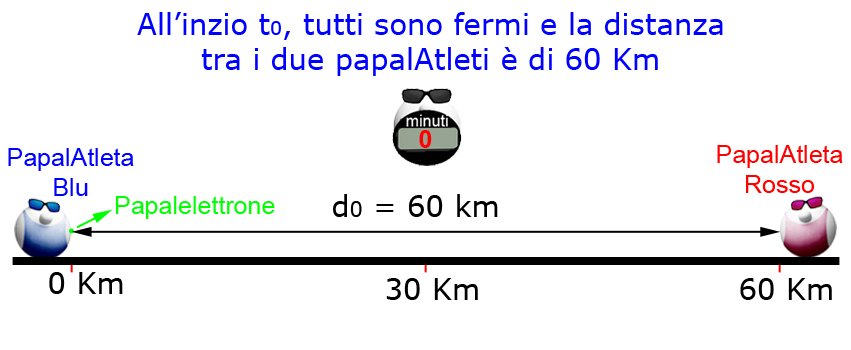
Papalogica si è subito messa all'opera......smontato i vari movimenti.
I PapalAtleti si muovono sempre alla stessa velocità Vp, quindi il tempo necessario ai due PapalAtleti per incontrarsi è indipendente da ciò che fa papalelettrone. Dato che i PapalAtleti viaggiano alla stessa velocità, ma in verso opposto, non possono che incontrarsi a metà strada.
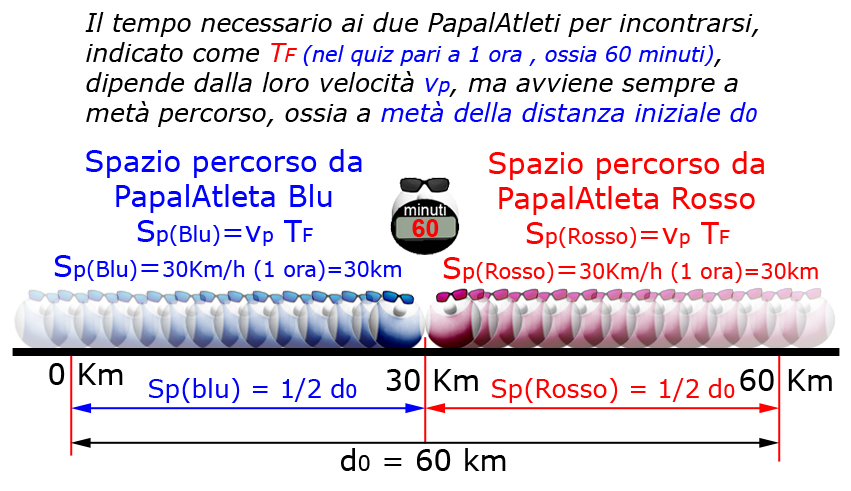
Il tempo finale TF non è altro che quello occorrente ad ogni PapalAtleta per compiere metà tragitto, ossia metà della distanza iniziale d0.
Il tempo occorrente è uguale allo Spazio percorso diviso la velocità, ossia:
t = S/v
Nel caso del quiz lo spazio percorso da ogni PapalAtleta è:
S = ½ d0 = 60/2 = 30 km
che viene percorso alla velocità vp di 30 km orari:
TF = 30 km/(30 Km/h) = 1 ora = 60 minuti.
Papalmatematico, non si lascia certo sfuggire questa regola generale che sembra caratterizzare qualunque gioco simile e la traduce sinteticamente come:
TF = ½ d0/Vp TF = d0/2Vp
A questo punto può entrare nel gioco anche papaleleltrone, la cui presenza non cambia ciò che succede ai due PapalAtleti.
Lui parte da inizio pista e viaggia ad una velocità Ve e dopo un certo tempo, che chiamiamo t1, raggiunge PapalAtleta Rosso.
Nel medesimo tempo t1, però, PapalAtleta Rosso si è avvicinato ad inizio pista fino ad incontrare papalelettrone.
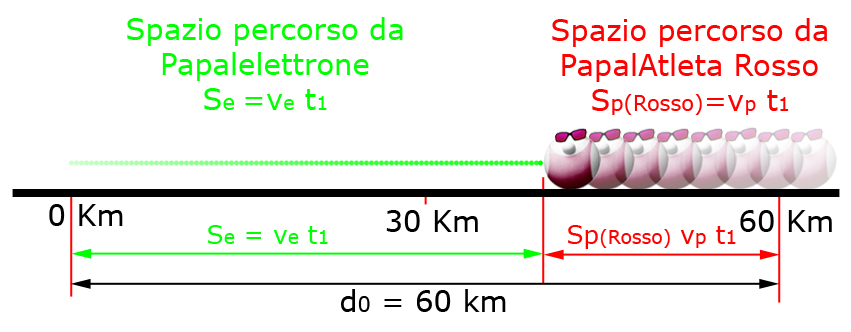
E' del tutto evidente che il tratto di pista percorso da papalelettrone Se sommato al tratto di pista percorso da PapalAtleta Rosso Sp (Rosso) devono essere uguali alla distanza iniziale d0.
Papalmatematico, sintetizza tutto in modo rapido e semplice.

Applicando il linguaggio di Papalmatematico al quiz, si ottiene facilmente che:
t1 = d0/(ve +vp) = 60 km/(60+30)km/h = 60/90 h = 2/3 ora
t1 = 2/3 ora = 2/3 60minuti = 40 minuti
Trovato il tempo in cui avviene il primo rimbalzo è facile ricavare lo spazio percorso da Papalelettrone e lo spazio percorso da papalAtleta Rosso:
Se = ve t1 = 60Km/h 2/3 h = 40 km
Sp (Rosso) = 30Km/h 2/3 h = 20 km

Papalogica, però, ricorda che mentre scorreva il tempo fino a t1, PapalAtleta Blu, si è spostato dall'inizio della pista e ne ha compiuto un tratto.
Ovviamente la quantità di spazio è identica a quella che nel frattempo ha compiuto PapalAtleta Rosso , dato che la loro velocità è uguale:
Sp(blu) = Vp t1
Essendo trascorso il tempo t1, i due PapalAtleti hanno accorciato la distanza che li separa ed ora si trovano ad una nuova distanza, indicata come d1.
Papalmatematico ha inserito vicino alla distanza d il pedice 1 (d1) per indicare che si tratta del primo rimbalzo di Papalelettrone, così come vicino a t il pedice 1 (t1) indica che si tratta del tempo necessario a Papalelettrone per raggiungere PapalAtleta e rimbalzare per la prima volta.

I Papalcuriosoni si consultano un attimo fra loro e affermano che ormai le regole del gioco sono chiare!
C'è una relazione che lega sempre la distanza precedente a quella successiva, rimbalzo dopo rimbalzo.
Papallino, che stava ascoltando i Papalcuriosoni, alza la mano e dice: ma io non ho ancora capito qual è questa strana relazione!
Va bene andiamo con ordine, rispondono i Papalcuriosoni, in fin dei conti per ora abbiamo visto solo cosa succede al primo rimbalzo.
Papalogica invita a soffermarsi sul fatto che, nel medesimo tempo t1, la distanza iniziale tra i PapalAtleti d0, si riduce alla distanza d1.
Papalmatematico mostra volentieri questa ovvietà.

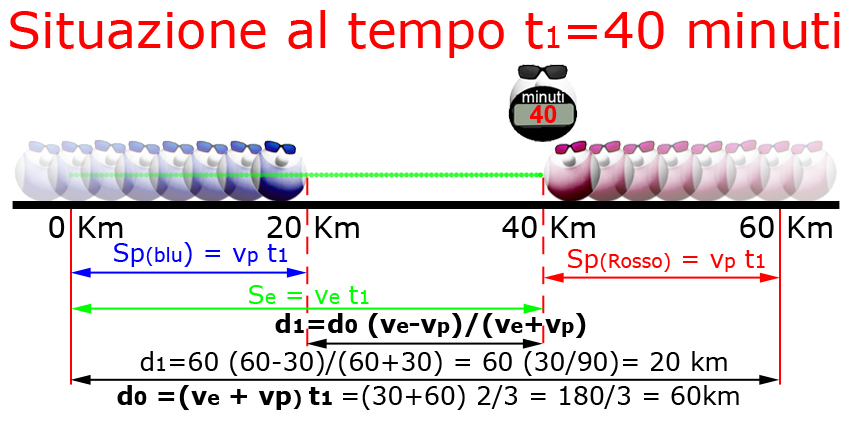
I Papalcuriosi sono sicuri che, la situazione sia destinata a ripetersi all'infinito, ossia:
d2 = d1 (ve – vp)/(ve + vp)
d3 = d2 (ve – vp)/(ve + vp) ...e così via.... per infiniti rimbalzi...
Fidarsi è bene, ma potrebbe pure esserci lo zampino di Papalscherzone, per cui meglio verificare questa strana predizione.
Vediamo cosa succede al secondo rimbalzo di Papalelettrone.
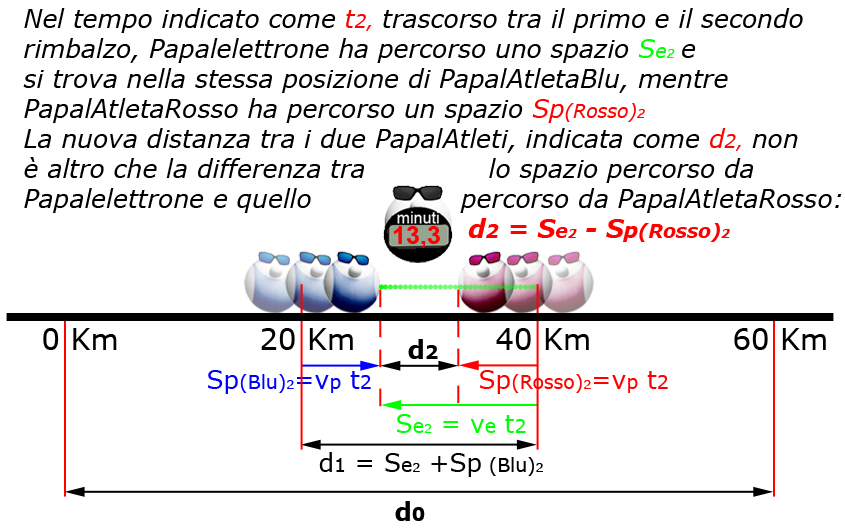
Papalmatematico è soddisfatto, perchè nell'intervallo di tempo t2 tra il primo e il secondo rimbalzo, accade come predetto, nuovamente la stessa cosa:

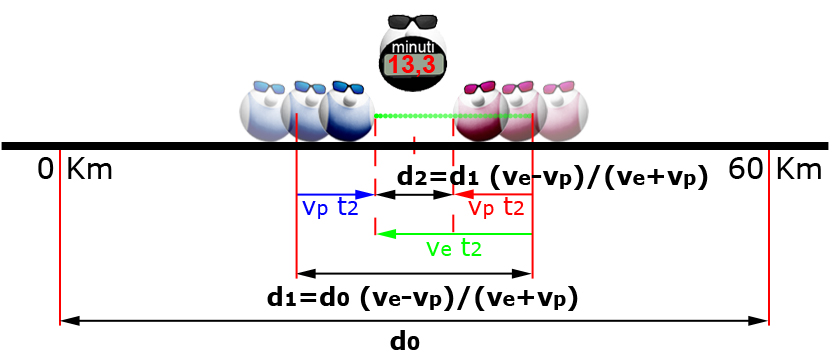

Ma qual è la misura di questa nuova distanza d2?
Figura 12: Quanto misura la nuova distanza d2?
Usando il linguaggio di Papalmatematico..... nel caso del Quiz, si ottiene:
d2 = 60 (60 - 30)/(60 + 30) (60 – 30)/(60 + 30) = 60 (30)/(90) (30)/(90)
d2 = 60 (1/3) (1/3) = 60 (1/9) = 6,66 km
Come trovare il tempo tra il primo e il secondo rimbalzo, era già stato indicato da Papalmatematico:
t2 = d2/(ve -vp) = 6,66/(60-30) = 6,66/30 = 0,22 ore
t2 = 0,22 ore = 0,22 (60 minuti) = 13,33 minuti
Infine lo spazio percorso dai PapalAtleti e quello da Papalelettrone:
Se = ve t2 = 60 km/h 0,22 ore = 13,33 Km
Sp = vp t2 = 30 km/h 0,22 ore = 6,66 Km
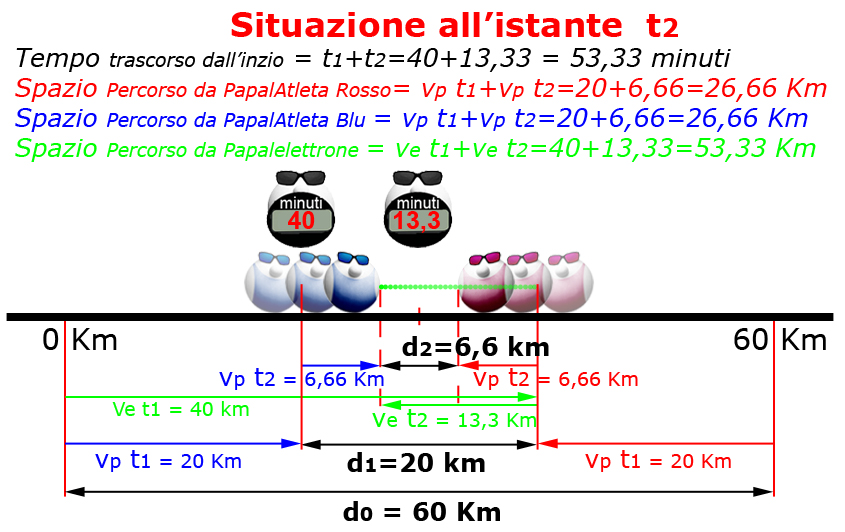
Papalogica invita a concentrarsi solo su ciò che succede a Papalelettrone.
Poco importa da quale PapalAtleta parte, poiché lui viaggia sempre più veloce del PapalAtleta su cui è appena rimbalzato, per cui è sempre un passo avanti rispetto a lui e anche se l'altro PapalAtleta si sta avvicinando Papalelettrone lo raggiunge prima del PapalAtleta da cui è partito.
Tale situazione si ripete ad ogni nuovo rimbalzo ed il povero Papalelettrone sembra destinato a rimbalzare un numero infinito di volte tra i PapalAtleti.

Papalmatematico, sorride nuovamente, poiché le predizioni si sono dimostrate esatte.

Più le distanze si accorciano, più si riduce il tempo tra un rimbalzo e l'altro!

Grazie a Papalmatematico è possibile conoscere ad ogni rimbalzo quanto distano i due PapalAtleti e quanto tempo è trascorso dal rimbalzo precedente.

Anche Papalmatematico, con i suoi calcoli, conferma che il numero di rimbalzi di Papalelettrone è infinito...
Più aumenta il numero di rimbalzi, più diminuisce la distanza tra i due PapalAtleti, finché questa al tempo TF si riduce a zero.
Più la distanza si avvicina a zero, più il numero di rimbalzi cresce e si avvicina a infinito.
Eppure i due PapalAtleti impiegano sicuramente un tempo finito, indicato come TF, per incontrarsi e nello stesso tempo la distanza tra loro deve ridursi a zero!
Questo è un dato di fatto e peraltro il tempo necessario ai due PapalAtleti per incontrarsi non dipende da ciò che fa Papalelettrone.
Papalogica, utilizza un gioco assai più noto per mostrare come la somma di infiniti piccolissimi segmenti possa produrre un risultato finito.

La similitudine proposta da Papalogica è facilmente applicabile anche al gioco che i Papalcuriosoni hanno ormai smontato in più pezzi.
Papalmatematico lo mostra in un attimo!

Nel caso indicato dal quiz la somma delle distanze è uguale alla metà della distanza iniziale d0/2.
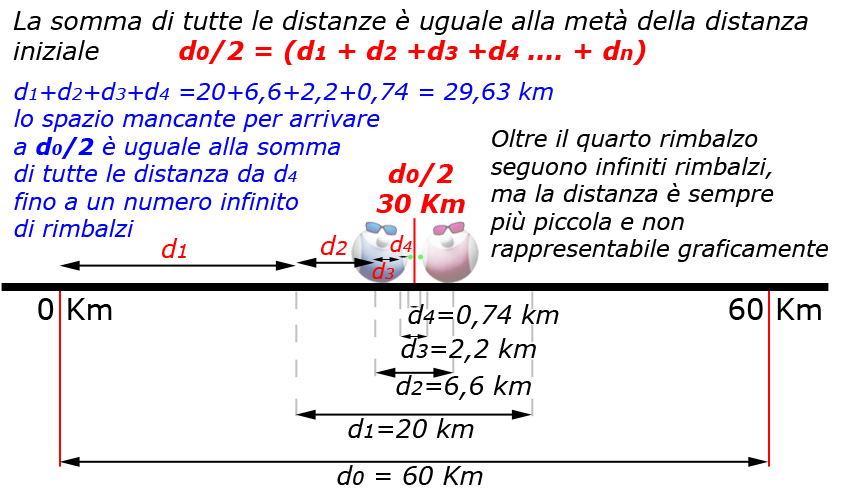
Smontando il gioco i Papalcuriosi sono in grado di applicare le sue regole ad ogni gioco simile, anche con distanza iniziale o velocità diverse da quelle proposte dal quiz (purché la velocità dei due PapalAtleti sia uguale).
Papalmatematico sintetizza tutto come solo il linguaggio matematico sa fare.

I Papalcuriosoni saranno anche soddisfatti che infiniti rimbalzi producano un esito finito e scontato, ossia l'urto finale tra i due PalaAtleti nel tempo previsto TF , ma Papalelettrone è un po' preoccupato di tutti quei rimbalzi.
E come in tutte queste occasioni echeggia l'urlo dei PapalCuriosoni: STOP AL PANICO!
Papalelettrone pur essendo davvero minuscolo ha un diametro stimato in 5,635 10-18 Km, perciò ha una dimensione fisica.
Se la distanza tra i due PapalAtleti si riduce ad una dimensione inferiore al suo diametro, è evidente che per Papalelettrone non c'è più spazio per rimbalzare, lui è inesorabilmente incastrato tra i due PapalAtleti.
Come al solito per calcolare dopo quanti rimbalzi Papalelettrone si incastra tra i due PapalAtleti ci pensa Papalmatematico.

Papalelettrone, con tutti quei rimbalzi infiniti che lo aspettavano, può tirare un sospiro di sollievo..... e di rimbalzi può limitarsi a farne solo quaranta...
Ora che il gioco è stato completamente smontato si può rimontare!
Grazie ai calcoli di Papalmatematico, PapalGrafico ha tradotto il linguaggio matematico in linguaggio grafico ed ha realizzato un'animazione del nuovo gioco. ... altro che la matematica non serve a niente!
Ad ogni rimbalzo viene misurata la distanza tra i due PapalAtleti mentre il cronometro segna il tempo trascorso tra un rimbalzo e l'altro..... la scala dell'immagine (papalli esclusi) è stata continuamente aumentata per mostrare distanze sempre più piccole.
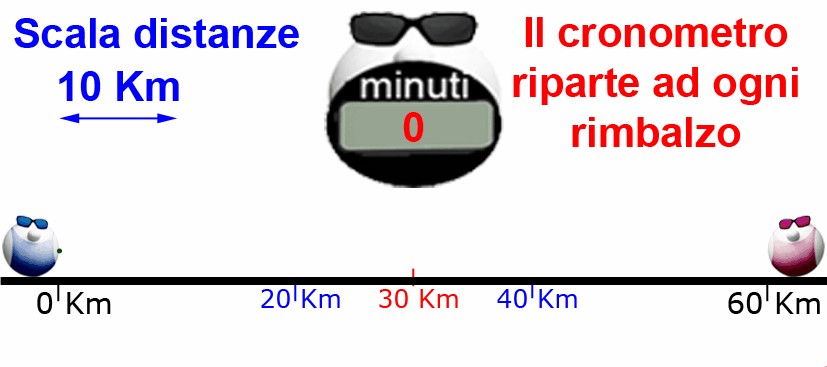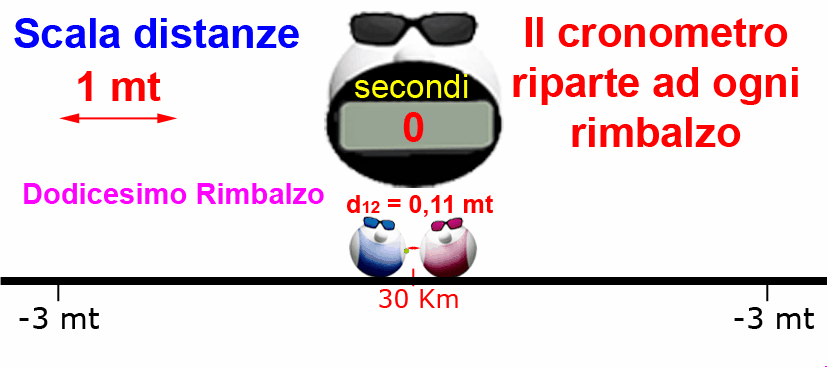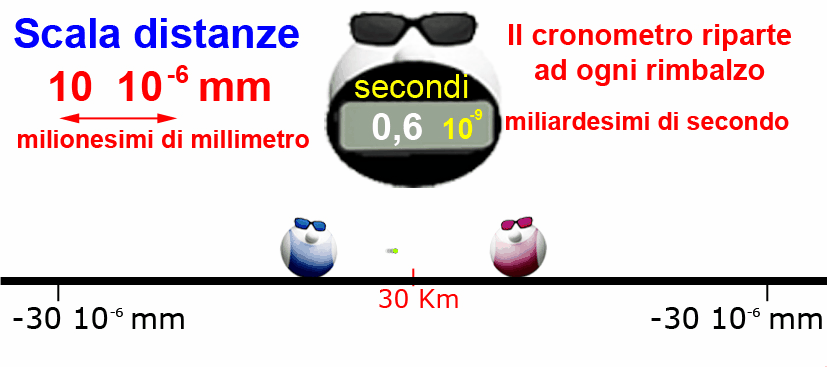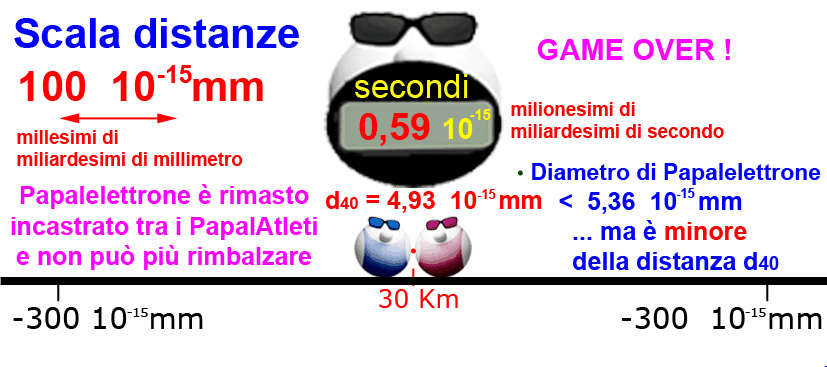
Quando Papalelttrone si incastra tra i PapalAtleti le grandezze sono nell'ordine dei millesimi di miliardesimi di millimetro per le distanze e nell'ordine dei milionesimi di miliardesimo di secondo per il tempo tra un rimbalzo e l'altro....
I Papalcuriosoni consigliano ai papalli ancora più curiosi di visionare la soluzione terricola del quiz QUI, molto più approfondita... e dare un'occhiata agli splendidi articoli su zero e infinito... il cui comportamento è diverso da quello degli altri numeri.. QUI QUI e QUI
Per oggi è tutto dal Pianeta Papalla
Mentre noi abbiamo sviscerato il viaggio di un elettrone che rimbalza tra due papalli, Gatto Gualtiero avrebbe voluto spiegarci come calcolare in un battibaleno quanta strada percorre una mosca che vola avanti e indietro tra due treni... ma aveva troppo sonno e, per questa volta, si è fatto sostituire dalla sua zampa destra Alan che, tuttavia, si è dimostrato all'altezza! Ecco QUI il loro video.






18 commenti
bravi ragazzi, veramente bravi... quando la curiosità diventa gioco!!!!
Non abbiate paura e leggete attentamente... chissà quanti esercizi riuscireste a trovare anche voi ter-curiosoni!
Ciao ragazzi!
Mi sono divertito un sacco a leggere questa storia e, ad un certo punto, mi sembrava di correre in su e in giù accanto al papalelettrone!!
Quindi una domanda mi è sorta spontanea: dopo quanti rimbalzi rimarrei incastrato, visto che il diametro del mio pancino misura 1 metro?
cari Papalliani... vi sto preparando un quiz che vi farà sudare quattro papalcamicie...


Mi fa piacere, Umberto, che ti stia divertendo... perché non provi a divertirti ancora di più, provando la soddisfazione di dare la risposta giusta?
E' una cosa da niente per uno bravo come te!!!
Per velocizzare i calcoli, voi terricoli potete anche impostare una tabellina su excel...
Cerco di farlo nel caso generale, bisogna usare i logaritmi
se^{n}) allora indicando con d il diametro del corpo che consideriamo:
allora indicando con d il diametro del corpo che consideriamo:
applico il logaritmo naturale ad entrambi i termini (il logaritmo è una funzione crescente)
per una proprietà dei logaritmi (il logaritmo di un numero elevato ad esponente, n, è dato da n volte il logaritmo del numero)
nel caso che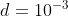
n dovrebbe essere 10
ho creato dei mostri... o -forse- lo erano già?????

Grande Umberto!
Infatti al decimo rimbalzo, la distanza tra i papalAtleti sarà di circa 1,01 metri quindi un istante dopo PapalScherzone rimarrà incastrato e chissà quale scherzo inventerà per liberarsi!!
Speravamo proprio in questa risposta che rende la storia ancora più completa per chi conosce il logaritmi (chi non li conosce e fosse interessato, ha l'opportunità di farlo seguendo il corso di matematica, li troverà alle lezioni 13 e 19).
GRAZIE
Come farò a liberarmi?! Semplice, il solletico funziona anche su Papalla
Dopo la risposta di Umberto, però, mi è sorta un'altra curiosità... per quanto tempo dovrò fare su e giù tra i papalAtleti prima di riuscire a fare loro il solletico???
Qualcuno vuole provare a rispondere?
sostanzialmente si può fare in due modi; o sfruttare il risultato precedente (n=10)
e calcolare la somma della serie parziale dei tempi, con n=10:
ricordando che:
(basta moltiplicare a sinistra per 1-x per rendersene conto)
tf=-0,99998306491219156971328896340328
oppure usando il termine generico della distanza fra i due in funzione del tempo:
ti=-0,99998333333333333333333333333333
ricordo solo che t è espresso in ore, quindi corrisponde a circa -59,999 minuti
Un'ora di corsa avanti e indietro?!
Meno male su Papalla non c'è attrito... Forse ce la faró!!!
Grazie Umberto!!
E un GRAZIE grande grande anche da noi, ovviamente!!
Boh... così umili e disponibili non usano la loro conoscenza "papalliana" per mire personali. Sarà, ma io non credo che i papallicoli siano terrestri... Vorrei vederli da vicino...
Non so Paolo, ma io di mire personali ne ho, eccome! Ti sembra poco acquisire tutta la conoscenza che Papalla elargisce gratis e divertendosi?! Altro che parole crociate per tenere il cervello allenato...

arrivisti!!!!
Ma come arrivisti?
Siamo appena partiti... al limite siamo partenzisti...
E poi su Papalla ci si diverte e non si finisce mai di imparare...... e come vedi amiamo raccontare i giochi e ciò chi ci sembra di aver imparato..... non siam proprio capaci di tenercelo per noi..... e le risposte dei terricoli le seguono anche su Papalla …....le usano per inventare nuovi giochi..... noi siamo solo delle umile pedine in questo interscambio cosmico.
Paolo
va bene, va bene, accetto la verità e mi fido di queste straordinarie creature...