Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Quello che abbiamo scritto è qualcosa di estremamente importante. Dimostriamolo in modo un po’ approssimato, ma essenzialmente corretto. Consideriamo la Fig. 2.

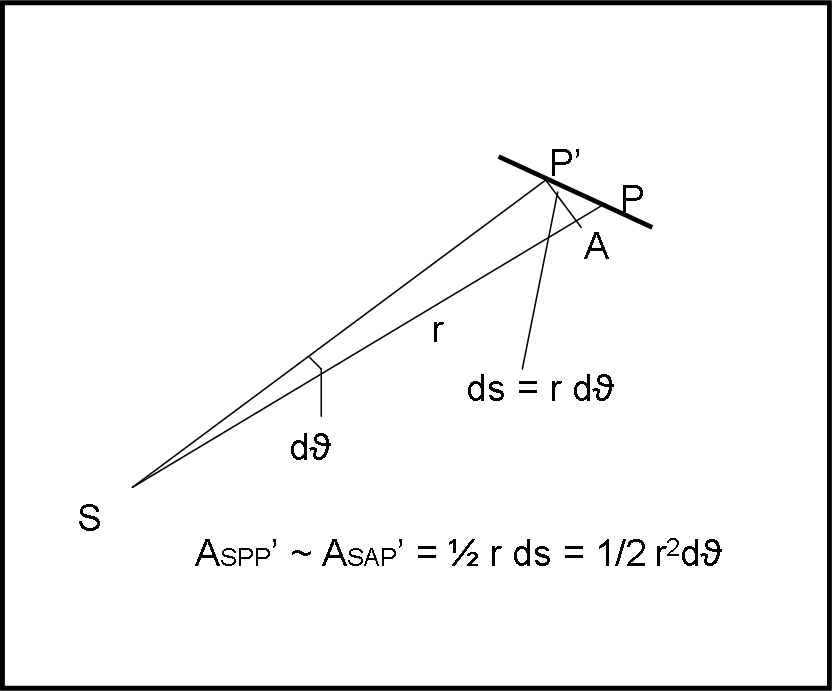
In un tempo dt molto piccolo il raggio vettore si sposta formando un angolo dϑ con il precedente. Se il tempo è infinitesimo possiamo considerare PP’ uguale ad AP’. L’area del triangolo SP’P può assumersi uguale a SAP’. Facendo tendere dt a zero, la faccenda si sistema anche matematicamente.

Quanto vale la sua area? Base per altezza diviso due. La base non è altro che r e l’altezza è ds = r dϑ (penso che non ci sia bisogno di spiegare questa formuletta, basta una proporzione…).

L’area è perciò ½ r ∙ r dϑ = ½ r²ϑ. Quest’area è funzione del tempo e possiamo calcolare come varia in funzione di questo, ossia possiamo calcolare la sua derivata che indica la velocità areolare descritta dal vettore r in un tempo dt. Essa è valida per qualsiasi  traiettoria e vale:

Velocità areolare = ½ r² dϑ/dt  = h/2  …. (30)

La (29) ci dice proprio che la (30) è una costante del moto, ossia descrive la seconda legge di Keplero.

Avrete sicuramente notato che l’espressione di β (da cui si ricava la seconda legge) indica praticamente che l’accelerazione normale al raggio vettore è uguale a zero. La costanza della velocità areolare è quindi una caratteristica dei moti in cui agisce una forza diretta verso il centro. Nel nostro caso questa forza è proprio quella di gravità.

Dimostriamo velocemente che il significato fisico di quanto detto è estremamente importante.

Il punto P viaggia con una velocità sempre tangente alla traiettoria. Calcoliamo il momento angolare, ossia il momento della quantità di moto.  Scomponiamo la velocità nelle sue due componenti: normale e radiale. Quella normale non è altro che r dϑ/dt. La velocità radiale v_r ci interessa poco e lasciamola pure nel vago. Infatti, eseguendo il prodotto vettoriale tra raggio vettore e componenti della velocità si ha che il modulo relativo alla componente radiale vale (α è l’angolo tra raggio vettore e componente della velocità):

L_R = m r v_r sinα = m r v_r sin(0) = 0

Il modulo del momento angolare è quindi solo quello dato dalla componente normale, ossia:

L = m r dϑ/dt r sin (90°) = mr²dϑ/dt     …. (31)

La (30), però, ci dice che:

½ r² dϑ/dt  = h/2

r² dϑ/dt  = h

Per cui la (31) diventa:

L = mr²dϑ/dt  = mh = costante

Per ricordare il momento angolare e il prodotto vettoriale potete andare  QUI (vi servirà anche dopo).

Ne consegue che la seconda legge di Keplero equivale a dire che il momento angolare di un corpo orbitante attorno al Sole è costante. Tanta fatica per così poco? In realtà ci si poteva arrivare subito… In altre parole, partendo dalla costanza del momento angolare si può arrivare velocemente alla seconda legge. Vale la pena dimostrarlo attraverso i vettori, in modo da richiamare il prodotto vettoriale ed eseguire un calcolo più … raffinato.

Potremmo partire con una semplice frase: dato che la forza è centrale, il suo momento deve essere ZERO e quindi deve essere costante il momento angolare. Ricordiamo ancora quanto si era detto e dimostrato QUI:  il momento angolare di un punto di massa m si conserva se è nullo il momento delle forze che agiscono su di lui. In questo caso l’unica forza agente è quella di gravità.

Vale la pena richiamare anche questa dimostrazione …

Sia L il momento angolare, F la forza e M il suo momento. Possiamo scrivere:

L =  r Λ mv

dL/dt = d(rΛ mv)/dt = (dr/dt) Λ mv + r Λ d(mv)/dt

Tuttavia, (dr/dt ) Λ mv = 0 (vettori paralleli). Se non ricordate perché, basta andare a vedere la Fig. 21 dell’articolo sul momento angolare (sempre quello di prima)...

dL/dt =  r Λ d(mv)/dt

Tuttavia, sappiamo molto bene che la derivata rispetto al tempo della quantità di moto non è altro che la forza F, per cui:

dL/dt = r Λ F = M

Ma, per definizione, r e F sono paralleli e quindi:

M = 0

In altre parole la derivata di L è uguale a ZERO e quindi L deve essere costante.

Procediamo, ricordando che cosa ci permette di calcolare il modulo del prodotto vettoriale: il modulo del prodotto vettoriale di due vettori v e u è uguale all'area del parallelogramma costruito sui due vettori.

(base per altezza, vedi Fig. 14 dell’articolo sul Momento Angolare). Ne segue che la metà di questa area è proprio quella del triangolo che vediamo nella Fig. 3

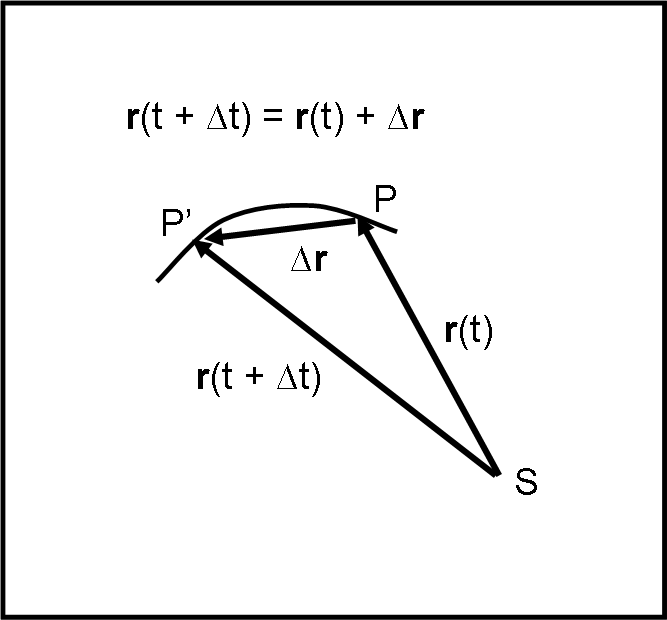
Questo triangolo ha come lati il vettore r = r(t) e il vettore r(t + ∆t) = r + ∆r . Possiamo considerare il vettore che unisce i loro vertici uguale alla curva PP'. L’approssimazione è più che valida, dato che facendo tendere ∆t a zero la curva coincide con il segmento.

Per quanto detto poco fa, la sua area vale, perciò:

∆A = ½ r Λ (r + ∆r)      …. (32)

r Λ r = 0

∆A = ½ r Λ ∆r

E la sua variazione con il tempo (la velocità areolare):

dA/dt = ½ lim _{∆t →0} ∆A/∆t = ½ lim _{∆t →0} (r Λ ∆r)/∆t = ½ r Λ lim _{∆t →0}(∆r/∆t) = ½ r Λ v

dA/dt = (r Λ v)/2

Ma sappiamo che:

L =  r Λ mv

r Λ v = L/m

Abbiamo appena dimostrato che L è costante e, quindi:

dA/dt = L/2m = costante

Nuovamente la seconda legge di Keplero

Come avete visto abbiamo agito con i vettori. Il fatto di aver trovato che il vettore momento angolare è costante vuole anche dire che la superficie in cui si svolge il moto deve essere un piano, dato che è l’unico modo per avere un vettore costante come modulo, direzione e verso.

In questo modo tutto si semplifica come calcoli, ma necessita di un’ottima conoscenza dei vettori e del momento angolare. Scegliete voi…

Tuttavia, per proseguire verso la prima legge di Keplero è meglio rifarsi ai calcoli analitici e tornare alla fine del terzo articolo (QUI).

Il nostro compito, adesso, è definire al meglio l’equazione differenziale da risolvere e non è cosa da poco.

Capisco che quanto svolto in questi ultimi articoli sembri molto impegnativo. In realtà non lo è, dato che abbiamo usato regole di cui dovremmo avere una discreta conoscenza. L’importante è affrontarle con la dovuta calma e attenzione. Le difficoltà sono state minime, ma, in compenso, siamo riusciti a dedurre la seconda legge di Keplero nel modo più generale possibile. E, credetemi, non è cosa da poco! Soprattutto abbiamo visto che essa non è altro che la conseguenza di una forza centrale che quindi non può far variare il momento angolare del sistema. Ed esso è dato, ovviamente, dal prodotto vettoriale tra velocità e distanza dal fuoco. Se cresce una deve decrescere l’altro e viceversa, ossia deve mantenersi costante l’area descritta dal raggio vettore nell’unità di tempo.