Categorie: Astronomia Elementare
Tags: altezza azimut nadir orizzonte primo sistema sfera celeste sistemi di riferimento zenit
Scritto da: Vincenzo Zappalà
Commenti:2
La Sfera celeste e i sistemi di coordinate. 2: Il primo sistema *
Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento
Presentiamo concetti estremamente semplici, sicuramente conosciuti da tutti. Tuttavia, dato che diventeranno i punti di riferimento dei vari sistemi usati per individuare gli astri e gli altri oggetti celesti, cerchiamo di definirli in linea con quanto detto finora sulla geometria sferica. Questo articolo segue la prima parte (QUI) e quelli relativi alle coordinate sferiche (QUI e precedenti), che sarà inserito negli approfondimenti..
Usciamo all’aperto in un luogo che abbia l’orizzonte il più libero possibile. Poco importa se è notte o giorno: sopra di noi appare in tutta la sua magnificenza la sfera celeste. In realtà, ne appare solo metà, dato che l’altra semisfera rimane nascosta sotto i nostri piedi. Se siamo di giorno essa è dominata da un bel cielo azzurro oppure coperto da nubi delle più varie sfumature dal bianco al nero. Un panorama bellissimo, ma che poco ha a che fare con l’astrofisica, ma piuttosto con la nostra atmosfera (in realtà tutto ciò che esiste fa parte dell’astrofisica…)
Al limite appaiono il disco del Sole, quello della Luna e, se siamo vicini alla notte, i pianeti più luminosi. Molto meglio osservarla quando è buio, soprattutto se il cielo è sereno. Tutto ciò solo se vogliamo utilizzare telescopi ottici, dato che gli astri mandano comunque la loro informazione elettromagnetica.
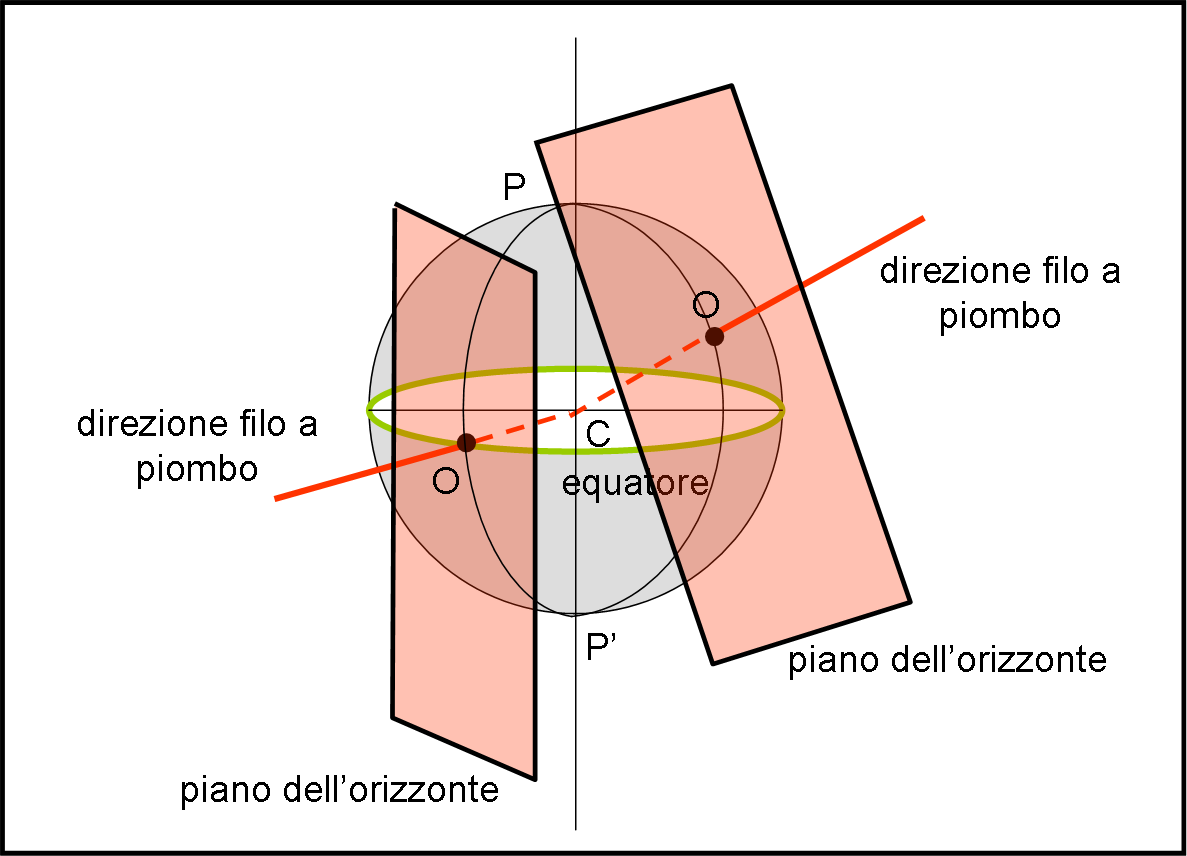
La prima cosa da fare è determinare la direzione del filo a piombo nella posizione O dell’osservatore e poi considerare il piano tangente alla sfera terrestre in quel punto, che è anche perpendicolare alla direzione del filo a piombo, ossia il piano dell'orizzonte (Fig. 3) .Questa retta e questo piano sono quelli fondamentali per il primo sistema di riferimento.
Consideriamo la schematica Fig. 4, dove vediamo diverse sfere celesti per diversi osservatori. Un osservatore qualsiasi O, O1 , O2 , O3 è posizionato in un punto della superficie terrestre e, come già detto, ha a disposizione un filo a piombo che gli permette di individuare la direzione OZ , O1Z1, O2Z2, O3Z3, che indica la verticale del luogo. Ricordiamolo fin d’adesso: per un qualsiasi osservatore, la verticale del luogo è una direzione fissa nel suo sistema di riferimento. Analogamente, per lui la sfera celeste sembra sempre la stessa, anche se prima o poi vede apparire l’alba e, se è attento, vede anche le stelle che compiono strani cerchi nel cielo. Per adesso, però, disinteressiamoci di ciò che si muove o -meglio- che sembra muoversi.
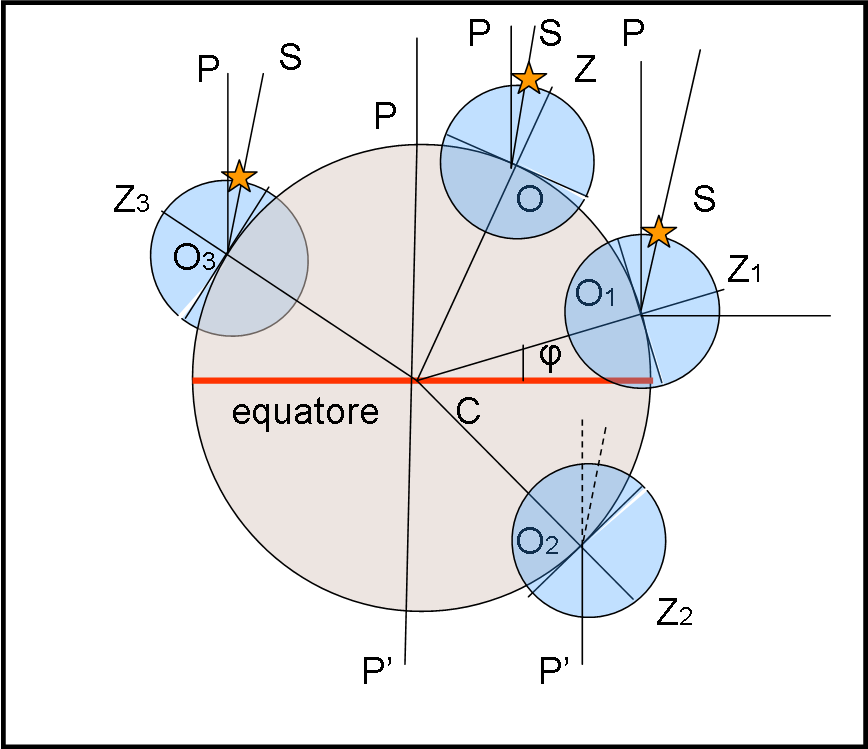
Il punto Z , Z1, Z2, Z3 ,… viene chiamato zenit del luogo (quello opposto, invisibile, si chiama nadir). Assumendo la Terra come una sfera perfetta, la verticale deve passare per il suo centro C. Come già detto, è facile determinare il piano dell’orizzonte che è, quindi, il piano tangente alla superficie terrestre nel punto O, O1, O2, O3, …
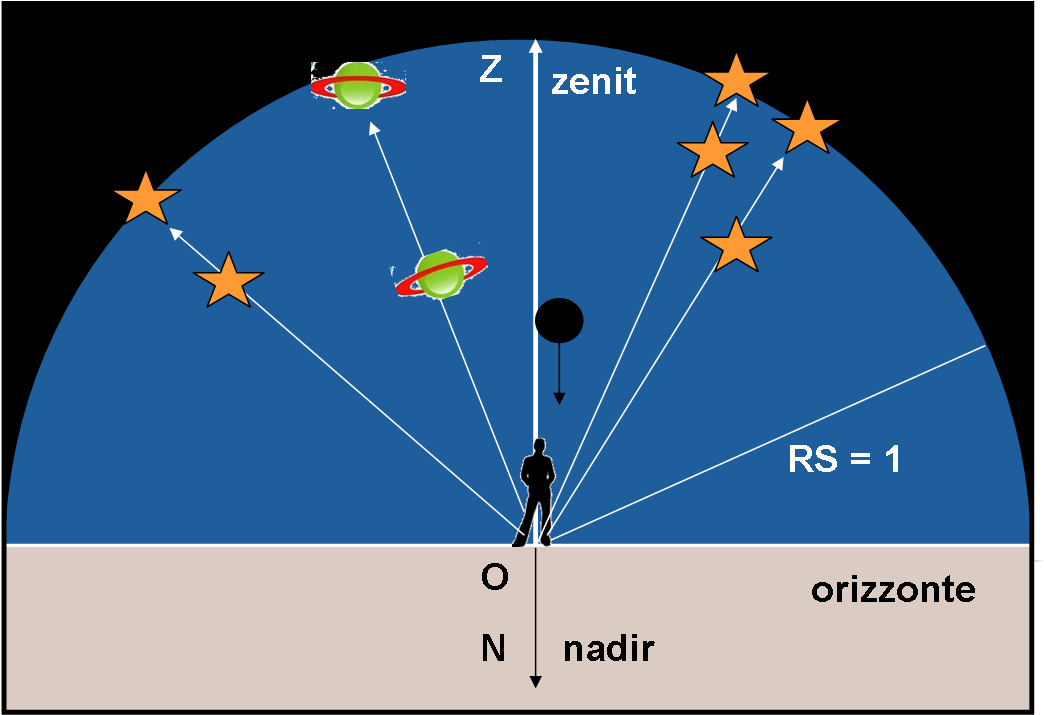
Ogni osservatore può facilmente disegnare la sua sfera celeste com'è mostrato in Fig. 5, dove vengono proiettati i vari astri, facendo riferimento al piano dell’orizzonte (e allo zenit). Il piano dell’orizzonte interseca la sfera celeste e identifica un cerchio massimo di centro O, che si chiama orizzonte celeste del luogo. Dato che misuriamo solo angoli tra gli astri, la sfera celeste di ogni osservatore ha un raggio indeterminato e possiamo, perciò, considerarlo unitario.
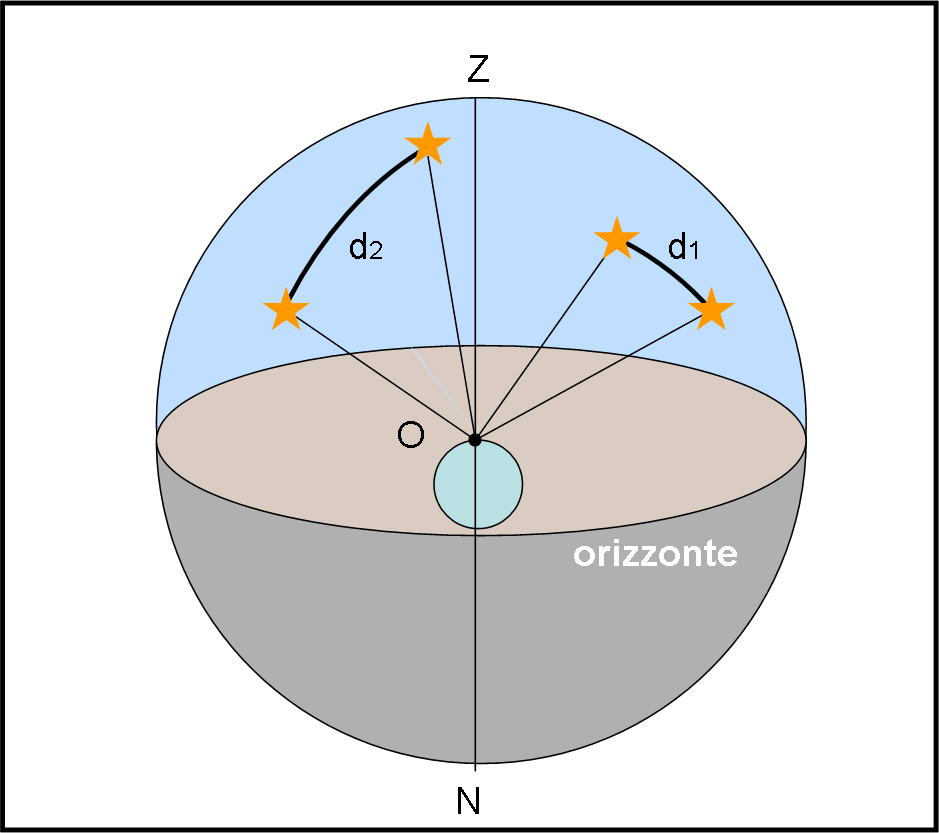
Vale la pena ripetere che la sfera celeste è una sfera fittizia che riproduce ciò che vede l’osservatore, il quale può ricavare solo le direzioni degli astri, ma non la loro effettiva distanza. Ne segue, anche, che la distanza apparente tra due astri è data dall’angolo compreso tra le loro direzioni o, più efficacemente, dall’arco di cerchio massimo (la minima distanza) che li congiunge, come descritto in Fig. 6.
Abbiamo assodato che, nella Fig. 4, quella che vede O1 non è lo stessa che vede O2 e via dicendo. Ciò è vero, dato che gli astri possono essere considerati (per lo più) a una distanza infinita e la loro luce giunge a noi secondo rette parallele. La posizione degli astri rispetto allo zenit e all’orizzonte celeste del luogo è quindi diversa da luogo a luogo, come si può notare nella figura. Le distanze angolari tra Z e S è diversa di quella tra Z1 e S e Z3 e S. Addirittura l’osservatore O2 non vede la stella.
Immaginiamo che la Terra sia immobile. Siamo già in grado di definire un sistema di coordinate celesti anche se sappiamo che si riferiscono solo al luogo dell’osservatore O. Il cerchio massimo fondamentale è quello dell'orizonte. Lungo la perpendicolare che passa per O si può subito identificare lo zenit Z.
Nella stessa figura, possiamo anche inserire una “stella” molto particolare. Non sappiamo bene cosa sia, ma è situata nella direzione perpendicolare all’equatore della Terra (questa informazione l’abbiamo già). Per gli osservatori che stanno “sopra” si chiama stella P, per quelli che stanno “sotto” si chiama stella P’. In realtà non è una vera stella, ma essendo determinata in ogni sfera celeste da rette tra loro parallele (e perpendicolari all’equatore), la possiamo tranquillamente indicare come tale. La stella P la vediamo già nella Fig. 4 (O2 non vede P, ma solo P’). Anche la stella P (e P’) ha una posizione sempre diversa rispetto all’orizzonte del luogo.
Nella Fig. 7 disegniamo, in tre dimensioni, la sfera celeste relativa all’osservatore O .
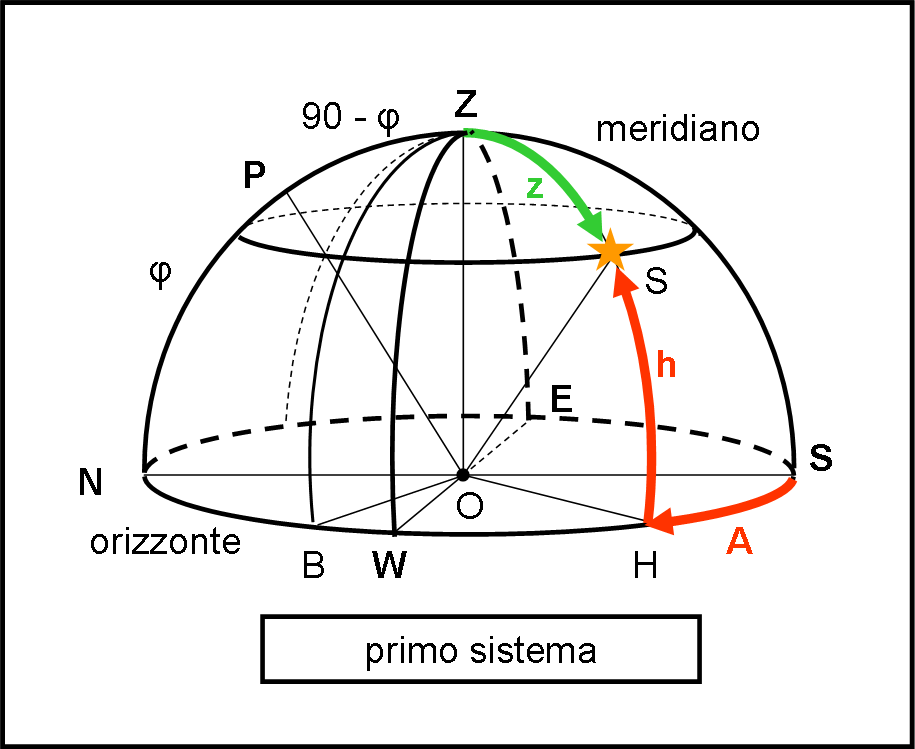
Si nota bene il cerchio massimo che passa per P (e per P’) e per Z. I punti in cui questo cerchio massimo incontra quello dell’orizzonte vengono chiamati N e S. N è quello più vicino a P. A 90° dal punto N, andando in verso orario segniamo il punto W. In direzione opposta alla sua segniamo il punto E. In parole povere, abbiamo segnato il Polo Nord celeste (P), il Polo Sud celeste (P’), Il Nord (N), il Sud (S), l’Ovest (W) e l’Est (E) e, ovviamente lo zenit Z.
Consideriamo una stella S. Prendiamo un piano parallelo a quello dell’orizzonte, che passi per S. Esso identifica un cerchio minore che ha una ovvia caratteristica: la distanza angolare dal piano dell’orizzonte è costante e viene chiamata altezza h. In figura, ovviamente, h è sia la lunghezza dell’arco SH, sia l’angolo al centro SOH.
Tutte le stelle che stanno su questo cerchio minore hanno la stessa altezza h. h è la prima coordinata di S. I cerchi minori paralleli all’orizzonte vengono chiamati paralleli d’altezza.
Tracciamo adesso il cerchio massimo che passa per lo zenit e la stella S, e tocca l’orizzonte in H. La seconda coordinata si misura lungo il cerchio dell’orizzonte partendo da S e andando in direzione di W fino a incontrare H. L’arco di cerchio SH (che è anche l’angolo al centro SOH) si chiama azimut A della stella S.
A volte, al posto dell’altezza h si usa l’arco complementare, ossia ZS, e viene chiamata distanza zenitale z.
Tutti i cerchi massimi che passano per Z si chiamano cerchi verticali. Quello che passa per N e S prende il nome di meridiano, mentre quello che passa per E e W si chiama primo verticale.
A questo punto non possiamo dimenticare che l’orizzonte varia da luogo a luogo, da cui si deduce che ogni astro S ha un’altezza diversa a seconda del luogo da cui è visto. Inoltre, cosa ancora più importante, la Terra non è immobile, ma ruota attorno al proprio asse (indicato proprio da P-P’) e quindi sia l’altezza che l’azimut di una stella sono costretti a cambiare da istante a istante. Notiamo anche che l’altezza del polo non è altri che la latitudine dl luogo.
Il sistema che abbiamo introdotto è il più immediato e semplice, ma si riferisce solo a un certo istante e a un certo osservatore. Se si volesse osservare una stella qualsiasi con un cannocchiale o un telescopio posizionato secondo questo sistema di riferimento, si sarebbe costretti a spostarlo a ogni istante, altrimenti l’astro scapperebbe velocemente dal campo dello strumento per effetto del moto di rotazione della Terra.
Prima di passare a un altro sistema di riferimento, che sia in grado di tenere in conto il moto di rotazione della Terra, può essere utile ai meno esperti “toccare con mano” cosa capita nel primo sistema, o sistema alto-azimutale, quando si osserva il cielo, introducendo una Terra che ruoti attorno a un asse perpendicolare all’equatore. Notiamo ancora una volta che l’asse polare (e quindi anche l’equatore) forma un angolo diverso rispetto allo zenit del luogo. La Fig 8 mostra immediatamente che questo angolo è il complementare alla latitudine del luogo φ (arco di cerchio massimo tra equatore e zenit), ossia: PZ = 90 – φ. Questa relazione ci sarà molto utile in seguito.
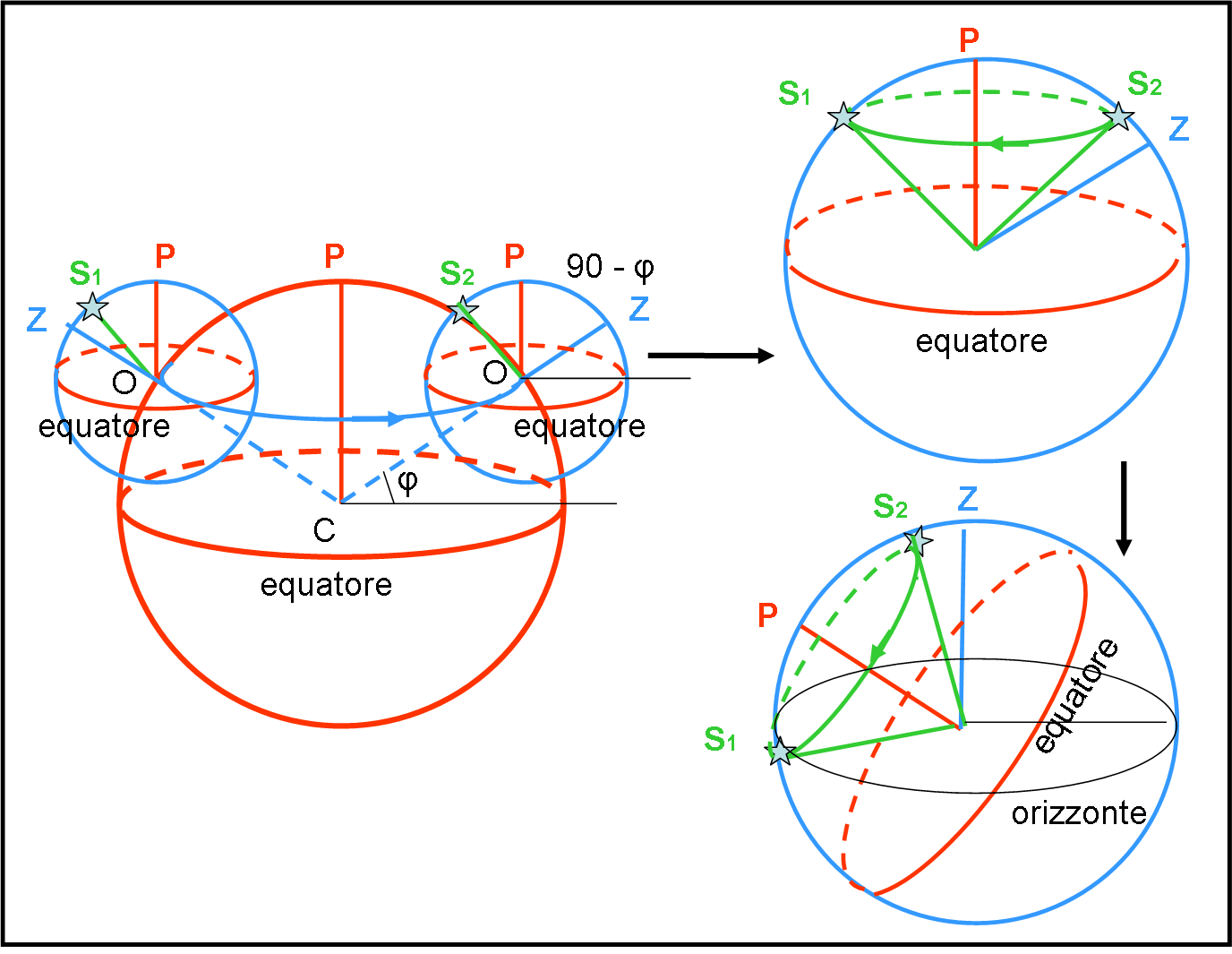
Quello che stiamo per scrivere è di una banalità irrisoria, ma, dato che ci siamo, spieghiamo anche le cose più semplici e ovvie. L’osservatore è posto in O (sul lato sinistro della Terra). In quella posizione il suo zenit è Z (non disegniamo l’orizzonte per non creare troppa confusione), ossia la congiungente centro della Terra e osservatore. La posizione di una certa stella sia S1. P è la solita direzione dell’asse di rotazione terrestre. Sia S1 che P non risentono assolutamente del moto di rotazione, dato che la prima è del tutto estranea al nostro pianeta, mentre il secondo è proprio la direzione dell’asse che è per definizione fisso (come già detto è una “stella” molto particolare).
L’osservatore O è costretto a spostarsi a causa della rotazione e descrive un arco di cerchio minore blu parallelo all’equatore (un parallelo, infatti). Lo zenit è obbligato a trovarsi sempre lungo la direzione ZC e questa, vista da un sistema di riferimento esterno alla Terra, descrive un cono di apertura 90 – φ. Chi, invece, vive sulla Terra, proprio in O, continua a vedere la direzione dello zenit sempre secondo la direzione del filo a piombo del luogo. Per lui non ha avuto alcun movimento. Ancora una volta il sistema di riferimento è essenziale!
Dopo 180° di rotazione, fermiamo un attimo la Terra. Per l’osservatore O, Z non si è mosso. Facendo coincidere Z (sfera in alto a destra), P rimane sempre al suo posto, mentre invece cambia completamente la distanza zenitale della stella, che è ora in S2. S1 era decisamente più vicina (e quindi più alta nel cielo), mentre, dopo mezza rotazione, si porta nella zona invisibile della sfera celeste, ossia poco sotto l’orizzonte.
Conclusione? L’osservatore O, convinto di essere fermo, vede la stella passare da S1 a S2 durante mezza rotazione terrestre, ossia in 12 ore. La situazione apparente nel sistema alto-azimutale, è quella della sfera in basso a destra.
Sintetizzando, ogni stella appare percorrere un cerchio minore (a meno che non si trovi proprio sul piano dell’equatore) parallelo all’equatore, in verso opposto a quello di rotazione della Terra. La "stella" P (o P’, per chi sta dall’altra parte dell’equatore) rimane invece fissa sulla sfera celeste (la rotazione avviene proprio attorno all’asse PP’).
Il Polo Nord ha la fortuna di avere (in questo momento storico, dato che anche l’asse della Terra si muove nel tempo) una stella estremamente vicina che, come già detto, prende il nome di Stella Polare (Alpha Ursae Minoris). Tutte le altre stelle descrivono cerchi minori in 24 ore. Questi cerchi non sono, normalmente, visibili completamente da O, dato che una parte è descritta sotto l'orizzonte. Ma su questa problematica avremo modo di tornare a lungo dopo l’introduzione del prossimo sistema di riferimento.
QUI trovate tutti gli articoli su questo argomento





2 commenti
Ehm.... ti sei perso un "si" in mezzo a una parola del secondo paragrafo...
grazie Mik!!!!!!!!!!!!!!!!!!! Oltretutto, era un "si" molto PESANTE...
