Categorie: Fisica classica Relatività
Tags: cinematica quiz relatività generale
Scritto da: Vincenzo Zappalà
Commenti:47
QUIZ su scimmiette troppo furbe e soldati incapaci **
Il quiz sul bicchiere pieno d’acqua bucato (QUI) è stato ormai risolto brillantemente da più di un lettore (primo fra tutti Pippo). Invece di dare la risposta ufficiale, descrivo due altri problemini che sono strettamente legati alla “causa” che non fa uscire l’acqua dal bicchiere bucato.
(a)
Il primo è veramente facile e non comporta alcun calcolo. Serve solo per generalizzare i risultati ottenuti per il bicchiere. Si prepara una specie di scatola chiusa in cui si inserisce il fucile A. Tracciando una retta perfetta dalla bocca dell’arma da fuoco si arriva a un chiodo B. Per complicare la faccenda e per testare la bravura del soldato e la precisione nella mira, tra il fucile e la parete in cui si trova il chiodo viene inserita una lastra di metallo con un foro F in perfetta corrispondenza della retta AB. Il foro è molto piccolo e permette il passaggio al proiettile solo se la sua traiettoria è perfetta.
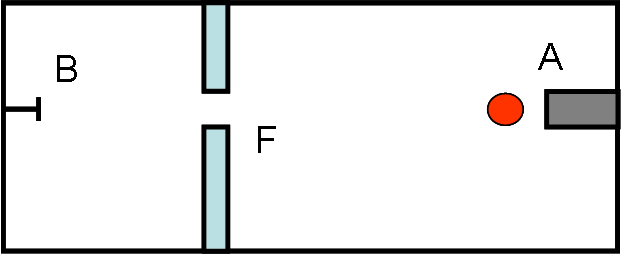Si dà il via all’esercitazione e… che pena! Dopo dieci tentativi, il soldato non è riuscito a fare un centro: tutti in proiettili sono finiti contro la parete di metallo e sono rimbalzati indietro.
(1) E’ veramente colpa della sua mira? (2) Cosa bisognerebbe fare affinché il soldato riesca a colpire il chiodo B ?
Come vi dicevo non c’è bisogno di tante formule, anzi solo un po’ di ragionamento e ricordare il bicchiere pieno d’acqua…
(b)
Il secondo quiz è un classico (per cui non cercatelo in giro per il web, se no perdereste il gusto della prova della vostra preparazione cinematica).
Un esploratore vuole catturare una scimmia di una razza molto rara e particolarmente intelligente (per poi liberarla dopo vari controlli sulla sua salute).
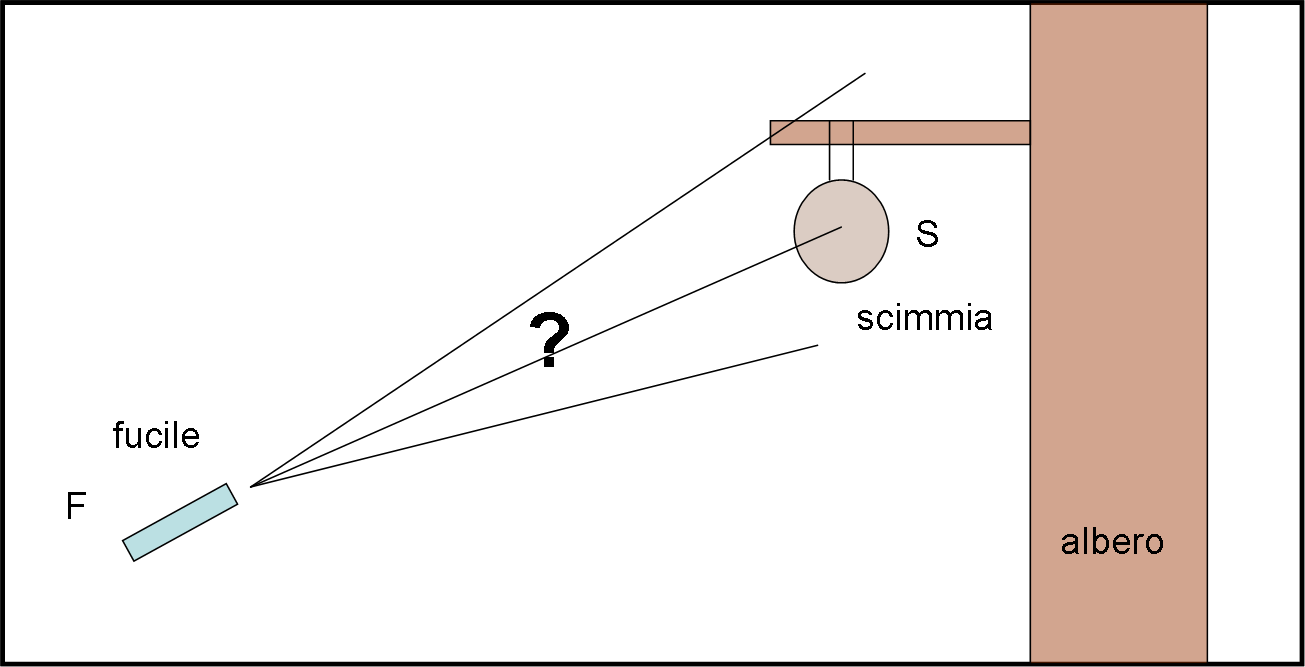
Non è facile e quindi sceglie di sparagli un proiettile che l’addormenti soltanto. Si munisce di un fucile F ad alta precisione e si incammina nella foresta. Finalmente, ecco un bell’esemplare S, appeso a un ramo di un albero molto alto.
L’esploratore si nasconde e inserisce un piccolo marchingegno che faccia vedere un lampo notevole, al momento esatto dello sparo (fuoriuscita del proiettile). Adesso è questione di prendere la mira… Conoscendo la furbizia di quelle scimmie, è SICURO che l’animale, appena visto il lampo, si lascerà cadere dal ramo.
Dove dovrà sparare l’esploratore per essere SICURO di colpire la scimmietta? Sopra la posizione attuale, sotto o esattamente nella direzione attualmente occupata dalla scimmia?
(1) Descrivere il tutto per via cinematica e (2) dimostrare che qualsiasi sia la velocità del proiettile (sempre che riesca ad arrivare fino all’albero, ovviamente) la scimmia non ha scampo e viene colpita e catturata.
Un doppio quiz, che risponde da solo al bicchiere pieno d’acqua, dà una “rinfrescata” di cinematica e apre la strada a un problema ben più importante legato alla Relatività Generale.
47 commenti
Il punto è sempre lo stesso, ma stavolta lascio ad altri il divertimento e taccio , altrimenti sembra che voglia dimostrare di essere bravo...!
Grazie Pippo!
Prego.
Ma il divertimento vero, che spero metterai di seguito, viene quando, nel primo caso, metterai un fucile che spara fotoni e uno schermo con un forellino cosí piccolo che lascia passare giusto un fotone alla volta.
I fotoni non hanno massa.
caro Pippo, la cosa non cambia, dato che lo spaziotempo rimane curvo anche per il fotone...
Se la scatola viene considerata "locale", almeno...
caro Pippo, non è certo una critica, la mia, ma voglio solo dire che sarebbe necessario veramente entrare nella RG, mentre per adesso basta la cinematica...
Hai anticipato il divertimento!
È vero che lo ST rimane curvo , ma per la geodetica tipo luce, si ha sempre :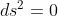
......
Ma non voglio parlare difficile, come tu dici non è ancora tempo per la RG.
Tuttavia, per suscitare la curiosità di altri lettori, lascia che dapprima risolvano il quesito cinematico con il proiettile materiale, e poi di' : che succede se al posto di un fucile che spara proiettili mettiamo un fucile che spara fotoni ? Andranno diritti ...passeranno per il buco....o no ? Ricordiamoci del calcolo banale dell'astronomo Soldner ( 1801) .....
Almeno , questo credo fosse il tuo intento.
Bah... Pippo, la mia intenzione era solo di limitarsi a corpi massicci e studiarne il movimento in condizioni particolari che sono poi anche molto comuni ... Dai, c'è tempo per la RG...
D'accordo, limitiamoci ai due tuoi quiz originali, lasciamo perdere i fotoni, come non detto. Se ne parlerà un'altra volta .
Però mi sembra che nessuno voglia cimentarsi, nè col proiettile nè con la scimmietta ....Forza ragazzi, non sono poi cosí difficili, se avete capito la storia del bicchiere con l'acqua !
Ciao Zappi,
riguardo al primo quiz, se il foro è delle stesse identiche dimensioni del proiettile (o appena appena più largo giusto per non farlo incastrare tra le pareti), sarà impossibile per il soldato colpire il chiodo. Infatti il moto del proiettile non è rettilineo ma parabolico, quindi sarebbe necessario allargare il foro in modo che al proiettile possa essere data la giusta angolazione.
Riguardo al secondo, siccome devo ancora finire inglese per domani, non ho tempo di impostare la soluzione per bene, ma, intuitivamente, visto che il moto del proiettile è parabolico, sparerei in un punto più in alto rispetto a quello in cui si troverà la scimmia dopo il lampo di luce, quindi sopra la posizione iniziale o anche verso la posizione iniziale, dipende dall’angolazione che si dà al proiettile che ne determina la traiettoria e quindi il punto di arrivo.
Ciao Valentina.
Enzo non se la prenderà se ti rispondo io .
Giustamente la traiettoria del proiettile è parabolica. Ma allora, a che serve allargare il foro di passaggio? Tu dici: per dare al proiettile la giusta angolazione... un po' verso l'alto, ovviamente, in modo tale che quando ricade dopo l'arco parabolico va a colpire il chiodo, che è il punto di atterraggio del proiettile dopo che ha descritto la parabola. E questo ci può stare.
Ma il fatto è che noi vogliamo che il fucile spari diritto in orizzontale , cioè quando il proiettile esce dalla canna del fucile la sua velocità (vettoriale) sia proprio orizzontale , non un po' verso l'alto , e non vogliamo allargare il foro sullo schermo, per nessun motivo....Perciò in queste condizioni il proiettile , che descrive una parabola ( la quale alla partenza ha tangente orizzontale) non entrerà nel foro ma colpirà lo schermo un po' più in basso....
Come possiamo fare per sparare il proiettile in orizzontale e farlo comunque passare nel foro ?
In quanto alla scimmietta , pensaci bene , l'intuito a volte consiglia male ! E nel pensare alla scimmietta , pensa anche a quello che abbiamo appena detto sul proiettile e il suo moto .
Grazie per i consigli, Pippo, ci penserò! Ora, però, ho sonno...
Giusto perché "se non vedo non credo" e non ho scimmiette a disposizione
, ho implementato la cinematica che regola il quesito (b) in geogebra. Non entro troppo nel merito delle relazioni invocate, lasciando la possibilità ad altri di rispondere. Sottopongo solo alla vostra visione il filmato molto breve da me realizzato mentre facevo variare l'angolo di sparo del proiettile, andando su e giù rispetto alla retta (rossa) passante per la canna del fucile e per la scimmietta. La parabola azzurra rappresenta la traiettoria seguita dal proiettile. Il punto E che vedete spostarsi verticalmente rappresenta la posizione occupata dalla scimmietta dopo un tempo t dallo sparo, visto che si lascia cadere esattamente in corrispondenza dello sparo. Il puntino nero, invece, rappresenta la posizione del proiettile dopo lo stesso tempo t.... Per rendere più evidente la posizione reciproca dei due punti, ho mantenuto la velocità di sparo del proiettile ad un valore basso. E' in pratica la trasposizione grafica del ragionamento analitico (cinematico).
https://youtu.be/EYHE4ztPl0M
Voglio aggiungere che l'angolo di tiro si può considerare sempre lo stesso e cambiare solo la velocità del proiettile (nel caso della scimmietta). Il risultato non cambia: la scimmietta non ha scampo se la mira è quella giusta...
Per Pippo (che scalpita
): facciamo così... fino a domani nessuna risposta e nessun aiuto ulteriore. Poi possono scatenarsi tutti. Nel caso della scimmietta vorrei una trattazione matematica semplice, di tipo puramente cinematico.
Questi quiz semplici servono per far pensare (anche se non si arriva al risultato) i meno preparati. Per gli altri è solo lavoro di... routine... e -magari- un breve ripasso.
So benissimo che Pippo, Paolo, Umberto, Fabrizio, Arturo, e altri (tanti spero) sanno la soluzione... mi piacerebbe che ci arrivasse qualche altro
Visto che non faccio parte dei più preparati, vorrei scrivere quello che ho pensato poco fa sul quiz del fucile.
Cercando di capire cosa c'entra il bicchiere in caduta libera, ho pensato che la particolarità sia la direzione della caduta, quindi ho realizzato che il fucile è inserito dentro una scatola e che forse questo espediente serve a poterla girare in modo che lo sparo avvenga in verticale (forse sarebbe meglio dire che il fucile deve puntare in direzione del centro di massa della Terra, ma essendo così breve il percorso del proiettile, credo che sia sufficiente appoggiare la scatola sul pavimento in modo che la direzione del proiettile sia perpendicolare ad esso). In tal modo i vettori velocità e accelerazione hanno la stessa direzione e il moto dovrebbe diventare rettilineo, non parabolico come quando si spara in orizzontale (o in qualunque altra direzione che non sia verticale) perché la direzione istantanea del proiettile è data dalla composizione vettoriale di velocità e accelerazione.
simpatica la tua soluzione, cara Dany ... ma, purtroppo, la scatola non può ruotare (mi dispiace) e inoltre la potenza del fucile non è tale da far giungere il proiettile fino al chiodo... a causa della forza di gravità che si oppone alla sua salita...
Comunque, non posso che dirti: brava! Una bella soluzione... ma si può risolvere senza rotazione e senza grande velocità d parte del proiettile... ricorda il bicchiere...
In realtà avevo pensato di sparare verso il basso, non verso l'alto... ma se dici che la scatola non può ruotare, allora a cosa serve? Ne possiamo fare a meno?
cari TUTTI. Posso chiedervi di risolvere il problema della scimmietta senza alcun bisogno della trigonometria?
Forse per qualcuno risulterà più semplice...
Pensando al bicchier d'acqua in caduta libera, mi viene in mente che acqua e bicchiere sono soggetti alla stessa accelerazione e quindi velocità istantanee... devo forse imprimere alla scatola la stessa accelerazione (in modulo, verso e direzione) data al proiettile dal fucile? Ma in tal modo, mi viene da pensare (anzi me l'ha suggerito Vale!) che il proiettile non raggiunga mai il chiodo... aspetta, forse ci sono... se imprimo alla scatola un'accelerazione che sia uguale in modulo e direzione a quella del proiettile ma verso contrario, dovrei ottenere un moto rettilineo del proiettile nella scatola e fargli raggiungere il chiodo perché questo gli andrebbe incontro... spero...
Dany... cosa succede al proiettile e ai fori se fanno come il bicchiere? Basta, però, se no influenziamo gli altri...
Mi stai, per caso, suggerendo di sparare mentre la scatola è in caduta libera?
Bene se influenziamo gli altri! Magari qualche "kamikaze" silenzioso potrebbe decidersi a darmi una mano...
Io sul quiz non dico nulla…
Una sola considerazione: perché i corpi in caduta libera subiscono tutti la stessa forza di attrazione gravitazionale, indipendentemente dalla loro massa m ?
.. e se la risposta fosse legata alle traiettorie obbligate, più brevi, in una geometria non euclidea?
Chissà perché questo quiz a me ha suscitato questa strana riflessione…
Paolo
Ops scusate
intendevo dire la stessa accelerazione di gravità e non Forza di attrazione gravitazionale..
F= ma
a =F/m
F (attrazione gravitazionale) = GMm/r²
a = GMm/mr² = GM/r²
Paolo
caro Paolo,
riflessioni più che giuste...
Non voglio andare nei dettagli per non anticipare discorsi su cui torneremo con maggiore calma e attenzione. Basti dire che quanto sia la massa che cade poco importa, dato che la traiettoria dipende solo da quanto la massa centrale (la Terra in questo cado) deformi lo spaziotempo attorno a lei. In RG non è giusto, infatti, dire che subiscono la stessa forza, dato che non vi è più una forza. Nel caso classico, si origina una forza (apparente) uguale e contraria che annulla quella di gravità.
In fondo è la stessa cosa che capita a un astronauta su un satellite artificiale. Su di lui agisce una forza uguale e contraria a quella di gravità che lo fa restare immobile nel sistema del satellite e senza peso... Anche lui è in caduta libera!
Vincenzo ,
i cavalli scalpitano , non gli esseri umani.
Daniela,
devi neutralizzare in qualche modo la gravita
ma io conoscevo un cavallo di nome Pippo... acci, non sei tu???!!
Per ora, caro Pippo, devo limitarmi a neutralizzare le scadenze fiscali di oggi
poi si vedrà...
Provo anch'io a dire la mia. Per il quiz del fucile che spara nel foro direi che (se la scatola e' ferma) non e' possibile per il proiettile passare dal foro e contemporaneamente colpire il chiodo, visto che questo e' allineato con una traiettoria rettilinea che congiunge la canna, il foro e il chiodo: infatti il proiettile compie una triettoria parabolica dovuta all'accelelrazione di gravita' e la parabola non puo' passare per i tre punti che congiunti dalla retta suddetta.
L'unico modo perche' il proiettile passi dal foro e' colpisca il chiodo e' che tutto il marchingegno (fucile, scatola, lamiera, chiodo) cada con l'accelerazione di gravita. In tal modo il foro e il chiodo accelereranno verso terra con la stessa che accelerazione del proiettile, e il moto relativo del proiettile rispetto alla scatola sara' rettilineo, esattamente come per il bicchiere d'acqua.
Il quiz della scimmietta e' simile. Di solito i cecchini regolano il mirino per compensare la traiettoria balistica del proiettile, che una volta uscito dalla canna si muove verso il basso con l'accelerazione di gravita, e quindi puntano la canna un po' piu in alto. Essi lo fanno perche' presumono che il bersaglio sia fermo.
In questo caso pero' l'esploratore sa che la scimmia si lascerà cadere, e siccome l'accelerazione di gravita' e' identica per la scimmia e il proiettile, all'esploratore bastera regolare il mirino parallelo alla canna, e poi sparare. Qualsiasi sia la velocita' del proiettile (ma anche la distanza della scimmietta) il proiettile la colpira': entrambi cadono ... e il moto relativo del proiettile rispetto alla scimmia e' rettilineo.
La trattazione cinematica sono un poco arruginito (e altri sono bravissimi...)...
@Enzo
No , io sono Βουκέφαλος , e oggi andiamo con Ale e Ari a far visita ad Alberto, perchè Ari vuole parlargli della sua Metafisica, e so che Alby gli parlerà invece della sua teoria. Non so se interverranno anche Gal e Isaac .
Risposta idiota: in BARBA ai fotoni la scimmietta davvero furba si sposta di lato
...
Risposta esatta, Luigi!!!
Ma quella scimmietta non è furba... è mia amica e ho fatto la spia per gettare un po' di scompiglio nel quiz!!
grande Luigi! La risposta ci sta tutta
Bene, dopo gli interventi di Paolo Salvini e quella fantastica di Luigi... diamo il via alle risposte accompagnate dalle formule (la più semplice avrà un encomio solenne da parte di Isaac e di Alby...).
PRONTI.... VIA!!!!! Liberate i cavalli....
quesito (b)
Siano dati :
H = altezza della scimmietta all'istante iniziale t=0
d = distanza orizzontale tra scimmietta e proiettile all'istante iniziale t=0
vo = velocità di sparo del proiettile
Indichiamo, inoltre, con t l'istante in cui il proiettile, dopo lo sparo, si trova sulla verticale della scimmietta.
Il moto del proiettile è parabolico , dato dalla composizione dei moti lungo i due assi cartesiani. Sappiamo dalla cinematica che lungo l'asse orizzontale x il moto del proiettile è rettilineo uniforme, quindi, se poniamo l'origine degli assi nella posizione iniziale del proiettile:
Lungo l'asse verticale y, invece, il moto del proiettile , nella fase ascendente, è uniformemente decelerato, quindi:
Abbiamo appena scritto l'espressione della quota a cui si troverà il proiettile all'istante t.
Passiamo alla scimmietta che si lascia cadere esattamente all'istante t=0. Il suo moto avviene solo lungo la direzione verticale ed è uniformemente accelerato, quindi:
Abbiamo appena scritto l'espressione della quota a cui si troverà la scimmietta all'istante t.
Noi vogliamo che il proiettile colpisca la scimmietta, quindi deve essere, all'istante t:
Quindi, per la (2) e la (3):
Dalla (1) mi ricavo t e lo sostituisco nella (4):
che posso scrivere come:
Non volendo ora utilizzare la trigonometria, consideriamo il triangolo rettangolo che ha per cateti H e d, e quello che ha per cateti le componenti della velocità iniziale del proiettile vo lungo l'asse y e l'asse x, La suddetta relazione, in pratica, dice che i due triangoli sono simili. E i triangoli sono effettivamente simili solo se il cacciatore mira esattamente alla scimmietta, né un po' più sopra né un po' più sotto. La relazione dice pure che la similitudine è indipendente dal valore della velocità iniziale vo. Aumentando o diminuendo tale valore, infatti, il rapporto tra le due componenti della velocità resta sempre lo stesso. Naturalmente, se vo dovesse essere troppo bassa, il proiettile non arriverebbe a colpire la scimmietta perché ricadrebbe al suolo prima di raggiungerla. Ma in tal caso il cacciatore dovrebbe buttare il suo fucile
Non dico ancora niente, ovviamente...
Volevo, però, comunicare che, per onestà, ho già scritto quella che è per me la soluzione più semplice e indicativa del problema. Dopo le risposte, la pubblicherò senza alcuna modifica e vedremo se, ancora una volta, qualcuno sarà più bravo di me. Ormai, la collaborazione sta vincendo...
scrivendo qualcosa farei un doppione della soluzione proposta da Arturo; del resto questo é un problema classico della fisica cinematica, difficilmente si può fare diversamente. Resterebbe di fare delle considerazioni sulla gittata ma senza trigonometria é un po arduo. Dal mio punto di vista vedo una casualità matematica sull intersezioni di due curve parametriche..
Secondo me l'ha fatto apposta, così come dice Luigi la scimmietta si muove di lato (in parallelo all'asse x) ed il cacciatore rimane senza preda
Io tifo per la scimmietta
Paolo
caro Paolo,
ho parlato di esploratore che vuole addormentare la scimmia e non ucciderla! Lungi da me la caccia...
caro Umberto,
si può impostare in modo diverso e trovare il valore passando da seno, coseno, etc... Lo so, per voi, sono banalità. ma speriamo che a qualcuno sia servito
La traiettoria parabolica del proiettile P ha equazioni parametriche ( il parametro è il tempo t ) :
la traiettoria lineare della scimmia S ha equazioni parametriche :
Nel punto di incontro delle due traiettorie ( supponendo che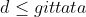
) , le ascisse devono essere uguali , e pure le ordinate devono esserlo, quindi deve essere :
cioè dalla prima :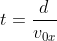
e dalla seconda :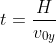
uguagliando i tempi , deve essere :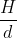
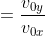
a secondo membro c'è il rapporto tra le componenti verticale e orizzontale della velocità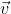
, che quindi deve essere uguale al rapporto tra altezza della scimmia da terra e distanza orizzontale della stessa dal cacciatore : il fucile va puntato nella direzione della scimmia.
Il rapporto detto non dipende dal modulo della velocità .
Sostanzialmente questa è la soluzione di Arturo .
@ Arturo
hai scritto :
Lungo l'asse verticale y, invece, il moto del proiettile , nella fase ascendente, è uniformemente decelerato, quindi: ......equazione (2)
guarda che l'equazione (2) vale sempre, non solo nella fase ascendente.
Non ho tempo di fare un disegno. Si vede anche (e si dimostra) che , conducendo in qualsiasi punto della parabola la tangente geometrica, (punto che rappresenta la posizione del proiettile in un dato istante) , questa incontra la traiettoria della scimmia nel punto in cui essa si trova in quello stesso istante, fino all'istante finale.
Cioè , istante per istante , il proiettile "guarda" la scimmia .
Attenzione però , che c'è un piccolissimo ritardo tra emissione del segnale luminoso dal fucile e ricezione dello stesso da parte della scimmia, a parte il tempo di reazione della scimmia.
caro Pippo,
a parte la soluzione che era ovviamente alla vostra portata (e ne sono ben contento), la faccenda della tangente alla parabola si dimostra immediatamente, sapendo che sia il proiettile che la scimmia subiscono la stessa accelerazione (gravità). Nel loro sistema di riferimento (caduta libera) è solo il proiettile che si muove con velocità uniforme. La velocità e proprio la tangente alla curva istante per istante, da cui segue che essa è sempre diretta verso la scimmia.
Basta mettersi nel giusto sistema di riferimento...
Probabilmente, il metodo più semplice è proprio fare questo ragionamento e dire soltanto che il sistema scimmia-proiettile è in caduta libera. Basta e avanza, direi...
La prossima volta, dobbiamo aumentare la difficoltà... siete troppo bravi!
Si, bastava dire che sono in "caduta libera" entrambi , e quindi nel comune riferimento dire che il proiettile si muove di moto rettilineo uniforme e colpisce inevitabilmente S.
Ma sai, spesso ho trovato arduo far capire che anche un proiettile che classicamente descrive una parabola, salendo e poi scendendo, in realtà è in caduta libera, basta trasformare le coordinate al riferimento accelerato .
ok
Caro Enzo, visto che la scimmietta viene solo sedata, mi cimento anch'io nella soluzione (ora ho accesso a Internet, ma non so quanto durerà
).
Preferisco usare due semplici figure, una che non considera la gravità e l'altra che introduce la gravità (come chiesto nel quiz).
E' mia intenzione proporre due soluzioni contemporaneamente, una che utilizza la scomposizione del vettore Velocità del proiettile (Vp) nelle sue due componenti Vpx e Vpy (parallele agli assi della ascisse e delle ordinate) e l'altra che utilizza seno e coseno...
Nella prima figura non viene considerata la gravità, per cui il percorso del proiettile è rettilineo e il fucile punta direttamente sulla scimmietta.
Non resta che introdurre l'accelerazione di gravità, che è identica sia per la scimmietta sia per il proiettile.
La scimmietta che si trova all'inizio (t0) alla distanza d dal fucile ed all'altezza h, viene accelerata verso il basso dalla gravità e dopo un certo intervallo di tempo t ha percorso verso il suolo uno spazio pari a: ½ gt²
quindi la sua altezza si è ridotta ed ora si trova nella posizione misurata sull'asse y:
y = h – ½ gt²
Ovviamente la sua distanza d (misurata sull'asse x) dal fucile non varia,.
Il proiettile durante la sua corsa subisce la stessa accelerazione di gravità, che frena la corsa verso l'alto del proiettile e nel tempo lo accelera verso il suolo.
Ciò significa che la componente della velocità Vpy (verso l'alto) viene ridotta dall'accelerazione di gravità.
Spy = Vpy t – ½ gt²
ma anche:
Spy = Vp sin α t – ½ gt²
Nel medesimo tempo, però, il proiettile per raggiungere la scimmietta deve percorre uno spazio d , misurato sull'asse x, pari a:
d = Vpx t
per cui il tempo t= d/Vpx
ma anche
d = Vp cos α t
per cui il tempo t= d/Vp cos α
Sostituendo il valore del tempo t necessario al proiettile per coprire la distanza d, nella relazione iniziale usata per determinare Spy, si ottiene l'altezza y raggiunta dal proiettile quando si trova alla distanza d :
Spy = y = Vpy t– ½ gt²
y = Vpy d/Vpx – ½ gt²
ma anche
Spy =y = Vp sin α t – ½ gt² = Vp sin α d/Vp cos α – ½ gt²
ma sin α/cos α = tan α
y = Vp tan α d – ½ gt²
Per raggiungere la scimmietta il proiettile deve arrivare alla distanza d, alla medesima altezza y nel medesimo tempo t, quindi deve valere che:
y scimmietta = y proiettile
y = h – ½ gt² = Vpy d/Vpx – ½ gt²
h = Vpy d/Vpx
Vpy /Vpx = h/d
ma anche:
y = h – ½ gt² = Vp tan α d – ½ gt²
h = Vp tan α d
Vp tan α = h/d
Ovviamente il percorso del proiettile non sarà più rettilineo, dato che con lo scorrere del tempo deve fare i conti con l'accelerazione di gravità, per cui la traiettoria, come mostra la figura, assume la forma di una parabola.
Spero di non aver commesso qualche errore...
Paolo
@ Pippo
Quando ho scritto che "Lungo l'asse verticale y, invece, il moto del proiettile , nella fase ascendente, è uniformemente decelerato, quindi:" mi riferivo al fatto che nella fase ascendente la velocità verticale del proiettile rallenta (decelerazione), mentre nella fase discendente aumenta (accelerazione). E' chiaro che l'equazione (2) è la stessa in entrambe le fasi, di salita e discesa. Infatti, nella implementazione grafica con geogebra del problema, di cui avevo pubblicato il link al video, ho considerato proprio quella equazione per il disegno della traiettoria parabolica. Comunque, è vero che il proiettile potrebbe in teoria colpire la scimmietta anche mentre esso sta ricadendo al suolo, non necessariamente mentre sta salendo. A tale riguardo allego l'immagine di un caso da me analizzato. Velocità proiettile 200 m/s, altezza scimmietta 40m , distanza cacciatore 500m.
Insomma , situazione direi molto improbabile.. Però in questo caso il proiettile , come si vede dalla figura, colpisce la scimmietta percorrendo il tratto discendente della parabola.
Nei casi pratici, tuttavia, il proiettile colpirà la scimmietta mentre è ancora in salita. Ecco un esempio grafico. Velocità sempre 200 m/s, altezza scimmietta 15m, distanza cacciatore 40m.
Questo il motivo per cui nel commento, a proposito della equazione (2), avevo circoscritto l'attenzione alla fase ascendente.
Circa il ritardo tra lampo e visione da parte della scimmietta, nonché suo tempo di reazione, considerazioni sicuramente corrette, le ho ritenute trascurabili non essendo state menzionate da Vincenzo nel quiz. Volendo approfondire, direi comunque, che il tempo di reazione della scimmietta sarebbe di gran lunga maggiore del ritardo dovuto alla velocità della luce, e forse proprio quello le risparmierebbe il disagio della puntura di anestetico..
ops.. terzo rigo del precedente mio commento: ovvio che non è la velocità che "rallenta", ma il proiettile. La velocità in realtà "diminuisce".
@Arturo
grazie per l'interessamento al mio commento, che ti ha portato addirittura a sviluppare dei casi pratici , con tanto di calcoli e diagrammi .
Ho accennato al ritardo dovuto alla propagazione del segnale luminoso (si tratta di 100 ns su una distanza di 30m lungo l'ipotenusa, una bazzecola
! ) per mettere un pò di pepe al quiz; altrettanto per il tempo di reazione della scimmietta, di gran lunga superiore . Chissà , magari la scimmia ha riflessi come i miei , che ho i dolori reumatici, e si salva ritardando il distacco... 
Ops,
in realtà un errore l'ho sicuramente commesso, nella parte trigonometrica ho trascinato un Vp di troppo, dato che:
Vp sin α/Vp cos α = Vp/Vp tan α = tan α
Ne segue che nella prima figura: h= d tan α (il Vp nella figura è di troppo)
mentre nella seconda figura: tan α = h/d (il Vp nella figura è di troppo).
Inoltre nella figura 2 la scimmietta è all'altezza iniziale h di 10 metri e la distanza orizzontale d è di 11 metri, mentre la velocità del proiettile è molto bassa (non vorrei far male alla scimmietta) ossia
Vpx= 10 m/sec e Vpy = 9,09 m/sec; per cui:
Vp² t² = Vpx² t² + Vpy² t²
Vp² = Vpx² + Vpy²
Vp= √Vpx² + Vpy² = 13,51 m/sec
Nella figura 2 ho indicato le posizioni del proiettile e della scimmietta ogni 0,1 secondi e l'impatto avviene dopo 1,1 secondi...
Sempre che non abbia commesso altri errori
..
Paolo
Bravi tutti ragazzi!
Quando si sono mossi i pezzi da "90", la faccenda è stata risolta in un battibaleno . Tuttavia, anche senza formule qualcuno aveva esposto (Paolo S, mi sembra) il concetto di base. Siamo di fronte a un problema di cinematica, che trova la sua comprensione più limpida nel cambiamento di sistema di riferimento, proprio quello che ha portato Einstein verso il principio di equivalenza.
Riporto comunque la soluzione cinematica e alcune frasi che ci facciano già passare verso il mondo della RG...
Mi sa che dovrò dividere i quiz in due categorie, in una delle quali non potranno mettere becco i nostri "cannoni"
Ma no, sto scherzando. Questi quiz servono a tutti: puro divertimento per i più bravi e fonte di apprendimento per i meno bravi. Quello che importa veramente non è risolvere, ma lavorarci sopra, divertirsi, magari lottare e, infine, imparare qualcosa di più. Nel nostro Circolo non esistono competizioni o classifiche. Siamo proprio come l'Universo... un 'infinito teatro in cui tutti giocano un ruolo fondamentale.