Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nell'  articolo precedente abbiamo parlato di generatori di gruppi e di gruppi liberi. Vogliamo ora provare l'esistenza di questi gruppi, senza ricorrere ad un esempio "reale".

Costruzione di un gruppo libero

Non è molto facile trovare  esempi di gruppi liberi, però c'è un procedimento astratto per costruirli.  Consideriamo un insieme S qualsiasi. Vogliamo da questo insieme costruire  (generare) un gruppo. Sia S={a,b,c,d,...}. Consideriamo tutte le sequenze (finite)ottenute combinando elementi di S in questo modo : acd, abd, daac, ecc..

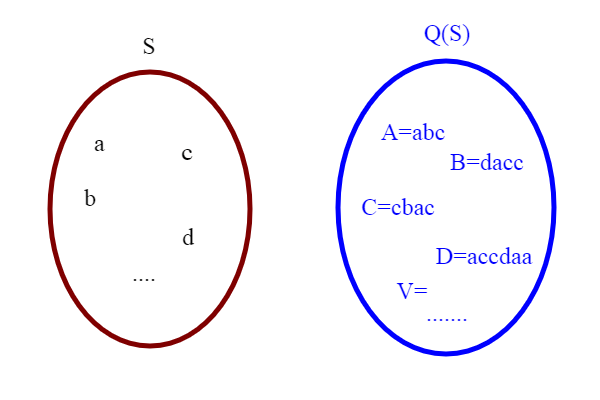
Chiamiamo queste combinazioni  o sequenze semplicemente parole. Definiamo Q(S) come  l'insieme di tutte queste parole. Notiamo che se anche S è finito, Q(S) è infinito.Infatti possiamo ripetere indefinitamente uno stesso simbolo quante volte vogliamo: abccccc,abccccccccccccc...... ottenendo tutte parole diverse.

Indichiamo le parole   con delle lettere maiuscole ; A=abc, B=cda, ecc. Definiamo (inventiamo) una operazione interna fra le parole di Q(S), in questo modo:

*: Q(S) x Q(S)---> Q(S) che (per esempio) ad A=acd, B=daac associa A*B=acddaac, ossia scrive semplicemente una sequenza dopo l'altra.

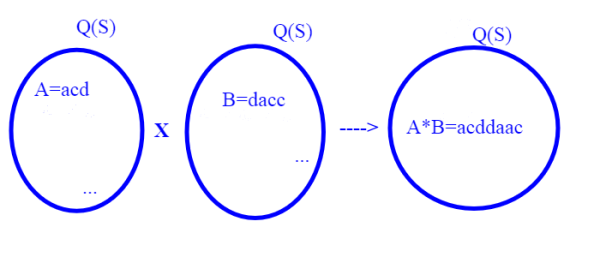
Chiamiamo  questa operazione. La giustapposizione di parole è una operazione interna(componendo due parole si ottiene ancora una parola) ed inoltre è  associativa . Sia C=abd una terza parola. Infatti è la stessa cosa comporre prima A con B e poi con C  oppure A  con B con C:

(A*B)*C=(acddaac)*abd=acddaacabd=(acd)*(daacabd)

quindi l'operazione * è associativa.

Non è commutativa : A*B=acddaacdaacacd=B*A.

Come elemento neutro prendiamo la sequenza vuota di lettere, che indichiamo con V.  Chiaramente combinando qualsiasi sequenza con la sequenza vuota otteniamo la sequenza stessa. Quindi V è proprio l'elemento neutro per questa operazione.

--------------------------------------------------------------------------------------------------------

(1)Giustapposizione:In linguistica, composizione di parole fondata sul semplice allineamento, senza che si stabilisca un rapporto di subordinazione dell'una all'altra o di entrambe a un'unità sintattica sottintesa.

--------------------------------------------------------------------------------------------------------

Nell'algebra astratta, un monoide è una struttura algebrica dotata dell'operazione binaria associativa e di un elemento neutro.

Q(S) è un monoide.

Per definire un gruppo questo ancora non basta; dobbiamo trovare per ogni elemento un inverso.

Dobbiamo in qualche modo ampliare l'insieme S; per ogni elemento a di S, prendiamo un elemento che chiamiamo ; per adesso questi elementi  non hanno niente di particolare, a parte il fatto che per ogni a ne esiste uno ed uno solo. Li chiamiamo al limite cancellatori. Come si può intuire tali elementi avranno il ruolo di essere gli inversi delle stringhe semplici, formate da una sola lettera, ma non abbiamo ancora risolto il problema degli inversi di ogni sequenza. Abbiamo così ampliato l'insieme S={a,b,c,d,.... a A={}. A viene anche chiamato alfabeto di S. Prendiamo  in considerazione gli elementi di W=Q(A) che adesso conterranno anche i nuovi simboli.

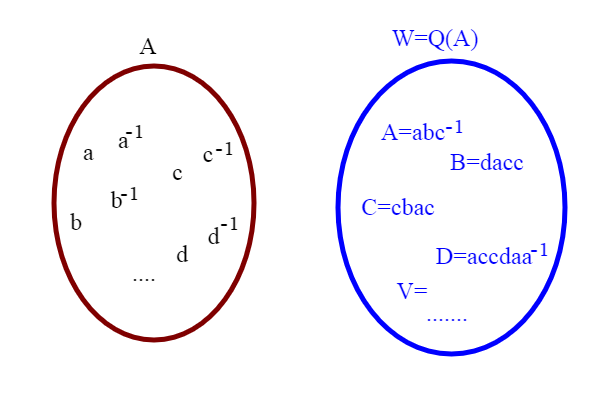
Sugli elementi w di W definiamo i seguenti due tipi di operazione:
(1) inserimento in w di una coppia di termini consecutivi del tipo  oppure  
(2) cancellazione in w di una coppia di termini consecutivi del tipo oppure

Diciamo  che due parole w1;w2 appartenenti a W sono equivalenti, e scriviamo , se w2 si ottiene da w1 mediante una successione finita di operazioni del tipo (1) o (2).Conveniamo inoltre che tali termini possano essere inseriti in qualsiasi punto di una parola, anche all'inizio o alla fine.

w=abc; parole equivalenti a w sono ad esempio:

,   ,    

la relazione è riflessiva:

;

infatti se a w prima aggiungiamo  e poi togliamo  otteniamo ancora w

Esempio:w=abc , 

è simmetrica:

se  allora ; infatti se w2 si ottiene da w1 mediante una sequenze di operazioni di tipo 1,2 se per ogni operazione poi facciamo l'opposta su w2 (nel senso che se era un inserimento facciamo una cancellazione e viceversa), allora da w2 otteniamo ancora w1.

esempio: ; se adesso togliamo    da w2 otteniamo proprio w1=abc;

è transitiva; se , , allora ; infatti se con operazioni del tipo 1,2 da w1 otteniamo w2, e se con operazioni del tipo 1,2 da w2 otteniamo w3, allora con una certa sequenza di tali operazioni da w1 otteniamo w3.

esempio: ; 

Indichiamo allora con [w] la classe di equivalenza di w; se  V è la stringa vuota, [V]=[]=[] qualsiasi sia x; (su V abbiamo effettuato un operazione di tipo 1).

Consideriamo adesso l'insieme quoziente; possiamo pensare alle parole ridotte, ovvero non contenenti sequenze del tipo  che tanto rappresentano la sequenza nulla. Così gli elementi ridotti potranno rappresentare tali elementi del quoziente (classi), così come le frazioni di Q (numeri razionali) possono essere pensate come ridotte ai minimi termini.

Definizione di un'operazione sull'insieme quoziente.

A questo punto è importante notare che per la costruzione del gruppo ci siamo spostati prima da Q(S) a Q(A), e adesso sull'insieme quoziente di  Q(A) rispetto alla relazione di equivalenza che abbiamo introdotto. Tale insieme si indica conF= 

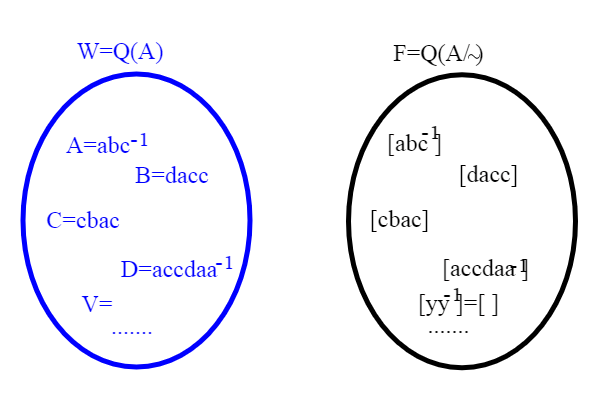
Sull'insieme quoziente definiamo l'operazione fra classi semplicemente così:

[w1]*[w2]=[w1w2] che si legge così: il risultato dell'operazione fra le due classi corrisponde alla classe della giustapposizione fra due rappresentanti qualsiasi. Perchè ha senso questa definizione? Perchè non dipende dai rappresentanti che scegliamo.Infatti se  allora . Vediamo con un esempio:  , ma il secondo membro è equivalente a per come abbiamo definito tale relazione.

Ci fermiamo qui per non appesantire troppo il discorso; nel prossimo articolo dimostreremo che con l'operazione che abbiamo definito sopra  diventa un gruppo libero.