Categorie: Curiosità Matematica
Tags: Club dei Maghi Elettricità Quazel quiz
Scritto da: Club dei Maghi
Commenti:18
QUIZ: L'infinito teatro delle luci di Quazel ***/****
Il nostro amico Quazel, trovandosi sulla Terra nel periodo delle feste natalizie, resta ammaliato dalle luminarie che addobbano il grande albero di Natale a Manhattan, la Torre Eiffel, le strade di tante città in Italia... Decide così di comprare un bel po’ di lampadine con cui realizzare, una volta tornato su Quazelandia, il suo pianeta, una luminaria da mostrare ai suoi quazel-simili. C'è solo un "piccolo" problema da risolvere: le luminarie sul suo pianeta hanno la particolarità di essere composte da infinite lampadine e con una luminosità sfumata.
Prima di partire, si reca in un negozio di articoli elettrici con l’intenzione di fare una bella scorta di lampadine. Per lui lo spazio è relativo, così come lo è il tempo, quindi non ha problemi ad immagazzinare infinite lampadine o ad aspettare un tempo terrestre infinito per averle...
Quazel: Buongiorno! Vorrei acquistare infinite luci colorate, come quelle che vedo in ogni angolo delle vostre case e delle vostre strade, quali mi consiglia?
Commesso: Lei è capitato nel posto giusto! Non tutti hanno un magazzino infinitamente fornito come il mio (sembra che solo un certo Cantor abbia un albergo con certe caratteristiche). Però, però... c'è un "piccolissimo" problemuccio tecnico: collegando un numero infinito di lampadine, che lo si faccia in serie o in parallelo, la luminaria non funzionerà mai!
Quazel: Che storia è questa? Non riesco proprio a capire... mi spieghi meglio, per favore!
Commesso: (Santa pazienza... questo tipo strano, oltre ad essere brutto e verde, deve essere anche un po' rimbambito!) Ok, ok... ci proverò! Dunque, deve sapere che la corrente elettrica consiste in un flusso ordinato di cariche elettriche (elettroni di conduzione) che si origina in seguito all’applicazione di una differenza di potenziale elettrico in due punti di un corpo conduttore, chiamata volgarmente voltaggio.
Quazel: E' chiaro, ma non capisco cosa c'entri tutto questo con le infinite lampadine che mi servono...
Commesso: Arrivo subito al punto... ogni lampadina oppone una resistenza al passaggio della corrente elettrica, più o meno come sabbia, pietre e vegetazione oppongono resistenza alla scorrere dell'acqua di un fiume. E, così come due pietre oppongono al flusso dell'acqua il doppio di resistenza di una sola pietra (tre pietre opporranno una resistenza tripla e così via...), lo stesso vale per la resistenza opposta da una o più lampadine al flusso della corrente elettrica.
Quazel: Ma certo! Queste cose le conosco benissimo!! Questo accade quando le lampadine vengono colegate in serie, infatti la resistenza totale è pari a Req = R1+R2+R3+….+Rn dove Rn sono le resistenze delle singole lampadine.
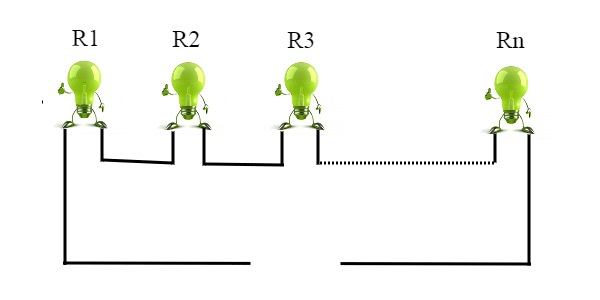
E so anche che se le colleghiamo in parallelo, invece, abbiamo Req= 1/(1/R1+/R2+1/R3+….+1/Rn)
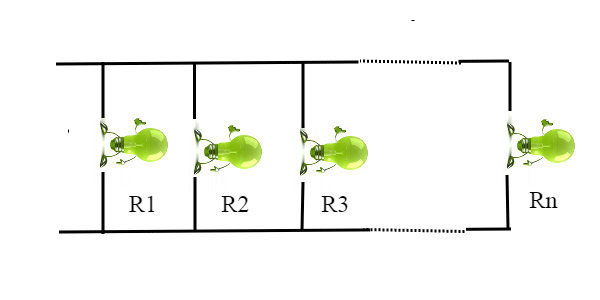
Commesso: (Mmm... forse non è rimbambito come sembra a prima vista, però non ha capito il succo del problema) Benissimo! Tutto giusto, ma allora non è difficile comprendere perché una luminaria con infinite lampadine non potrebbe mai funzionare: collegandole in serie, avremmo una resistenza infinita quindi la corrente non passerebbe e le lampadine rimarrebbero spente; collegandole in parallelo, invece, avremmo una resistenza nulla (il limite di Req per n che tende a infinito è pari a zero) e, non appena collegate all'alimentazione elettrica, tutte le lampadine verrebbero frantumate dalla corrente e sentiremmo solo un bel botto provocato dal corto circuito!
Quazel: Il suo ragionamento non fa una piega, ma le garantisco che esiste un modo per far funzionare una luminaria composta da infinite lampadine! Se, poi, ognuna di esse opponesse al passaggio della corrente una resistenza pari ad 1 Ohm, la luminaria diventerebbe addirittura... AUREA!!!
Commesso: Ma come è possibile?!
A VOI LA RISPOSTA: Quazel sta pensando ad un metodo fantascientifico realizzabile solo su Quazelandia, oppure questa luminaria infinita potrebbe essere realizzata anche sul nostro "pallido puntino blu"? Avete una settimana di tempo per rispondere, prima che Quazel si decida a spiegarci cosa fare, sempre che sia possibile... ;-)
Umberto e Arturo Lorenzo
QUI la soluzione del quiz
QUI trovate gli altri quiz del Club dei Maghi
18 commenti
Una così e una cosà, ripeti senza stancarti, sempre uguale, senza fretta.
Se della infinita catena il primo anello spezzerai, nulla cambierai, e da tutte le celle la risposta avrai.
E l'aurea davvero troverai.
Caro Maumau,
direi che la salute va meglio... Evviva!!!
chissà cosa voleva dire Maurizio..
Se non ho compreso male il problema, io userei un serie infinita di lampadine in parallelo, per cui la resistenza equivalente tende a zero, intermezzata da alcune lampadine (una seria finita) in serie, la cui resistenza equivalente sarà uguale ad un numero finito..
Sommando queste due resistenze equivalenti, la resistenza risultante sarà uguale ad un numero finito, per cui passa una certa quantità di corrente e non si creano cortocircuiti...
Paolo
Ok per la serie. Ma in parallelo non capisco, la corrente viene divisa per gli infiniti percorsi, quindi come fa a bruciare le lampadine. Qualsiasi numero diviso infinito è zero.
Gimar, Il problema di infinite lampadine in parallelo non è delle lampadine ma del generatore che dovrebbe erogare una corrente infinita. E' un tipico caso di "corto circuito" con resistenza di carico nulla. Certamente le lampadine non si accenderebbero perché il generatore smetterebbe subito di funzionare.
Paolo, prova a pensare di alternare una lampadina in serie ad una in parallelo ( una così e una cosà) in modo sistematico...non dimenticare che alla fine, utilizzando infinite lampadine da 1 ohm, devi ottenere un preciso risultato della resistenza equivalente
Nel testo si parla di lampadine frantumate...
Caro Gimar,
delle implicazioni fisiche non ti preoccupar...
che il problema delle lampadine in parallelo sia "così" o sia "cosà", il quiz per via matematica si risolverà!
Se la metti così...
Si può provare con: una lampadina in serie, una in parallelo con una in serie, con una in parallelo con una in serie ecc. ecc.
La resistenza totale dovrebbe essere la serie: 1+1/2+1/4+1/8+1/16 + 1/32..... in OHM naturalmente.
Forse una cosa non è stata detta in modo esplicito; la soluzione si compone in una parte grafica (descrizione del collegamento delle luci) e di una parte matematica (calcolo delle resistenza equivalente). Nella prima parte (purtroppo)è necessario un disegno.
Il circuito si compone di una serie infinita di celle tutte uguali, costituite da una lampadina (resistenza R) in serie, seguita da una in parallelo, e così via...
Sezionando la rete dopo la prima cella vediamo a sinistra la prima resistenza in serie, seguita da una resistenza che si trova ad essere in parallelo a tutto il resto della catena di resistenze.
Essendo la catena di lunghezza infinita, la resistenza equivalente a tutte le celle (tranne la prima) è identica alla resistenza equivalente comprendente anche la prima cella.
Req = R + R*Req/(R+Req)
R*Req + Req2 = R2 + R*Req + R*Req
Req2- R*Req - R2 = 0
Req = ( R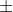
(R2 + 4*R2)1/2)/2
Req = R*( 1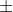
5 1/2 )/2
La soluzione negativa implicherebbe un valore di resistenza negativa, non la consideriamo.
Il valore della resistenza equivalente è quindi Req = R* (1 + 5 1/2)/2 e nel caso di R=1 ohm coincide con il valore della sezione aurea.
Aveva ragione Quazel: anche un numero di lampadine infinito può essere alimentato senza danni e fornire la luce per la festa.
Mi spiace per la parte grafica, ma sono negato.
Posso aggiungere un'altra possibilità: la prima lampadina può anche essere in serie, poi prosegue come prima.
In questo caso la resistenza sarà: 1/2+1/4+1/8+1/16 ... ecc. sempre in OHM
Scusa volevo dire: la prima in parallelo...
scusa Maurizio, quello che hai scritto può essere interessante, ma riusciresti a scrivere quelle formule con Latex? Non so se tutti abbiamo compreso le formule
Ripeto integralmente il post per comodità di chi legge....
Il circuito si compone di una serie infinita di celle tutte uguali, costituite da una lampadina (resistenza R) in serie, seguita da una in parallelo, e così via...
Sezionando la rete dopo la prima cella vediamo a sinistra la prima resistenza in serie, seguita da una resistenza che si trova ad essere in parallelo a tutto il resto della catena di resistenze.
Essendo la catena di lunghezza infinita, la resistenza equivalente a tutte le celle (tranne la prima) è identica alla resistenza equivalente comprendente anche la prima cella.
Req = R + R*Req/(R+Req)
R*Req + Req2 = R2 + R*Req + R*Req
Req2- R*Req - R2 = 0
Req = ( R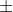
√ (R2 + 4*R2) )/2
Req = R*( 1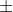
√ 5 ) /2
La soluzione negativa implicherebbe un valore di resistenza negativa, non la consideriamo.
Il valore della resistenza equivalente è quindi Req = R* (1 + 5 1/2)/2 e nel caso di R=1 ohm coincide con il valore della sezione aurea.
Aveva ragione Quazel: anche un numero di lampadine infinito può essere alimentato senza danni e fornire la luce per la festa.
Aggiungerei che la soluzione è solo una delle infinite realizzabili con lampadine da 1 Ohm che, opportunamente disposte, portano al medesimo risultato.
Scusate ma succede una cosa strana... mentre compongo le formule con Latex le vedo scritte correttamente, tuttavia una volta inviato il post, la formattazione scompare.... magari avete qualche suggerimento?
Intanto invio l'immagine del manoscritto...
Ciao Maurizio,
non ho ben capito cosa hai fatto, comunque le formule latex vanno scritte direttamente nei commenti cliccando sulla fx in alto a destra di questo riquadro, dopodiché devi cliccare su "copia in un documento" che compare sotto la formula.
Grazie Daniela, ora è OK. Chissà cosa ho combinato...