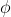Soluzione del quiz: Le luci di Quazel e... un quiz nella soluzione!
L'unica soluzione concreta data dai lettori al quiz è quella giusta. Lo schema di collegamento della soluzione è il seguente(al posto delle lampadine mettiamo il simbolo di resistenza)
lo schema si ripete all'infinito.
Dato che ci sono un numero infinito di resistenze, saranno ancora infinite se stacchiamo le due resistenze iniziali; le L rovesciate che compongono il circuito sono infinite; se togliamo la prima L (anzi anche se ne togliamo un numero finito da sinistra) il circuito rimane sempre lo stesso, essendoci una perfetta simmetria. Forse questo è un po' difficile da afferrare, ma è una cosa analoga all' albergo di Hilbert. Sta di fatto che in ogni caso, così procedendo, la resistenza totale non viene alterata.
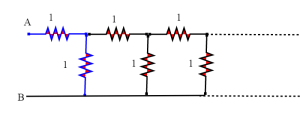
Ciò significa, come mostrato in figura (B), che la resistenza vista guardando verso destra tra C e D sarà uguale alla resistenza vista tra A e B. Sia R questa resistenza. E inoltre tale resistenza è finita. Non può infatti essere infinita: se supponiamo infatti per assurdo che lo sia, il parallelo di R con 1 ohm sarebbe ancora 1 ohm, e andrebbe in serie ancora ad 1 ohm, quindi varrebbe 2 ohm, ma questa è ancora R, contro l'ipotesi che R sia infinita.
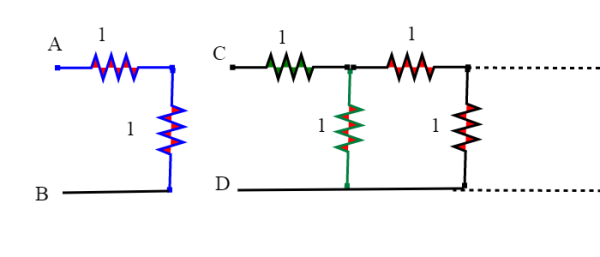
Ora sostituiamo la rete a destra di C e D con la sua resistenza equivalente, R, come mostrato in figura (C). La resistenza vista tra A e B sarà ancora R. Questa è la resistenza di 1 ohm in serie al parallelo di R ancora con 1 ohm
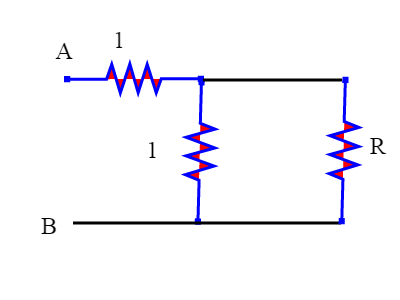
Ricordiamo ancora una volta le formule per le resistenze in serie e in parallelo:
Serie: Rs=R1+R2
Parallelo: 1/(1/R1+1/R2)= R1 R2/(R1+R2)
quindi nella figura C abbiamo:
R(1+R)=R+1+R
le due due soluzioni sono :
la prima è negativa e quindi è da scartare
quindi R=
Questo è un numero molto noto: si chiama rapporto aureo. E'solo una coincidenza?
Un altro approccio
Vogliamo cercare di esprimere la resistenza equivalente vista dai punti AB utilizzando un metodo ricorsivo, che ci permetta di visualizzare anche dei risultati intermedi.
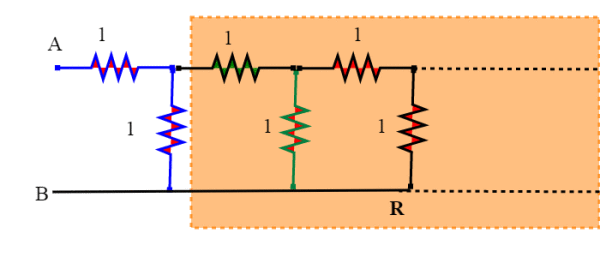
Chiamiamo ancora R tutta la resistenza che rimane nella zona arancione a destra e che si estende all'infinito; non sappiamo quale sia. In ogni caso la Req=R sarà data dalla resistenza blu in serie al parallelo fra l'altra resistenza blu e la R:
Ripetiamo adesso lo stesso ragionamento e consideriamo il blocco successivo
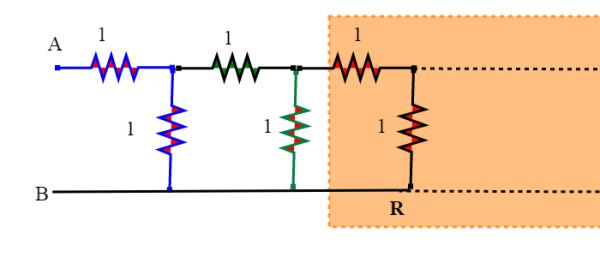
quello che vale sempre è che infatti la coda di destra è sempre R; sostituiamo allora ad R la sua espressione in modo ricorsivo e proseguiamo iterativamente.
questo tipo di espressione viene chiamata in matematica frazione continua, in questo caso frazione continua semplice (i numeratori sono tutti uguali a 1); "continua" perchè continua all'infinito, senza mai fermarsi. Voi mi chiederete adesso a cosa è servito tutto questo procedimento, per spiegarlo mi serve introdurre prima il concetto di sezione aurea.
Facciamo una piccola pausa sul quiz e ricordiamo velocemente cos'è.
Sezione aurea
Il nome sezione aurea è molto recente: lo si trova come goldener schnitt in un testo tedesco del 1835, Die reine Elementar-Mathematik di Martin Ohm, fratello minore del fisico Georg Simon Ohm che altro non è che l'inventore della legge di OHM (coincidenza con il quiz?).
Che cosa hanno di speciale la sezione e i rapporto aureo da attrarre l’attenzione, e non solo, dei matematici da almeno 2500 anni?
Sono numeri che compaiono nei contesti più disparati e permettono di gettare legami inattesi tra discipline all’apparenza distanti tra loro. Storicamente, la sezione aurea ha a che fare con il seguente problema geometrico: il calcolo (appunto) della sezione aurea.
In geometria la sezione aurea di un segmento è quella parte del segmento che è medio proporzionale fra l’intero segmento e la parte di segmento rimanente.
AB: AS = AS : SB
Indichiamo con l la misura di AB e con x la misura di AS: la misura di SB è l – x.
Determiniamo il valore di x in funzione di l.
Nella proporzione sostituiamo ai segmenti le misure delle rispettive lunghezze:
l : x = x : (l - x)
Applichiamo la proprietà fondamentale delle proporzioni:
,
risolvendo l'equazione di 2° grado otteniamo due radici:
che però è negativa ed è da scartare
l'altra soluzione è ;
Pertanto il rapporto tra la sezione aurea di un segmento e il segmento stesso risulta:
;
mentre invece il rapporto fra il segmento e la sezione (detto anche rapporto aureo) risulta essere l'inverso:
;
il rapporto aureo di solito si indica con :
quindi la sezione aurea si indica con:
:
La nostra resistenza equivalente altro non è che il rapporto aureo
Notiamo una particolarità del rapporto aureo:
quindi:
;
se a secondo membro sostituiamo ancora l'espressione di otteniamo:
procedendo così otteniamo:
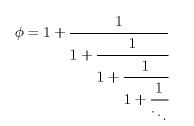
Che è proprio la nostra resistenza equivalente del quiz:
Se consideriamo ora i primi sviluppi della frazione continua:
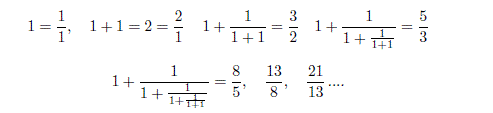
1, 2,3/2,5/3,8/5,13/8,21/13,34/21,55/34. . . notiamo sono tutte approssimazioni successive di
.
Comunque teniamo a mente queste frazioni, capiremo subito il legame fra rapporto aureo e altri numeri molto famosi...
I numeri di Fibonacci: il problema.
Fibonacci introdusse i suoi numeri con il seguente problema: quante coppie di conigli si otterranno in un anno da una coppia, supponendo che ogni coppia produca ogni mese una nuova coppia la quale sia in grado di produrre un’altra coppia dal secondo mese?
Formalizziamo il problema di Fibonacci chiamando Fn il numero di coppie adulte presenti al mese n e fn il numero di coppie non adulte presenti nello stesso mese.
Il modello di popolazione proposto da Fibonacci si descrive con il requisito
Fn+1 = Fn + fn
fn = Fn−1
per cui si ottiene la definizione ricorsiva
Fn+1 = Fn + Fn−1
Per completare, occorre precisare che al mese iniziale n = 1 si ha F1 = 1.
Vediamo in dettaglio con un esempio:
Nel primo mese, abbiamo solo la coppia di partenza.
Nel secondo mese, abbiamo nuovamente la coppia di partenza, che nel frattempo è diventata pronta a generare un’altra coppia di conigli.
Nel terzo mese, la coppia di partenza ha generato una coppia di conigli, che non è ancora fertile. Quindi le coppie sono diventate 2 di cui una sola è fertile.
Nel quarto mese, la coppia di partenza ha generato un’altra coppia di conigli. La coppia ottenuta al passo 3 è diventata fertile, ma non ha ancora generato un’altra coppia. Quindi le coppie ora sono 3, di cui 2 fertili.
Nel quinto mese, le due coppie fertili hanno generato un’altra coppia ciascuna. Quindi le coppie di conigli sono diventate 5; le due coppie appena nate non sono fertili, mentre le altre 3 lo sono.

La successione di Fibonacci.
Ricordiamo che una successione di numeri naturali altro non è che una funzione di
N-->N.
La successione di Fibonacci, (che indichiamo con F: N-->N) è una successione di numeri interi positivi in cui ciascun numero è la somma dei due precedenti. Chiaramente riusciamo a fare questo se n≥3
Poniamo:
F(1)=1, F(2)=1
per n≥3
Per calcolare un termine della successione è necessario procedere in modo iterativo, calcolando prima i precedenti, non possiamo farlo in modo diretto. Per esempio vogliamo calcolare F(6):
F(6)=F(5) + F(4)
F(5)=F(4) +F(3)
F(4)=F(3) + F(2)
F(3)=F(2) + F(1)
quindi: F(3)=2, F(4)=2+1=3, F(5)=3+2=5, F(6)=5+3=8
I primi termini della successione di Fibonacci sono: 1,1,2,3,5,8,13,21,34,55,...
Se adesso torniamo alle approssimazioni del rapporto aureo che avevamo trovato prima:
1,3/2, 5/3,8/5,13/8,21/13,34/21,55/34.. notiamo che tali frazioni altro non sono che rapporti del tipo ;
questo ci suggerisce che il rapporto aureo potrebbe essere
Per dimostrare questa affermazione ci serviamo di una famosa formula del matematico Binet che ci dà il termine n-esimo della successione di Fibonacci:
La formula di Binet
Questa formula è sorprendente perché esprime i numeri di Fibonacci, che sono interi, utilizzando operazioni algebriche eseguite su numeri irrazionali.
Per dimostrarla, consideriamo la seguente identità algebrica:
(per verificarla basta fare banalmente i due prodotti a destra, visto che il denominatore a-b è lo stesso)
se poniamo:
allora A0=0; A1=1 (estendiamo a 0 la successione,per far in modo che A2=A1+A0=1)
cerchiamo adesso due numeri a,b tali che:
a+b=1
ab=-1 se li troviamo la 1 diventa:
e troveremmo proprio i numeri di Fibonacci.
sappiamo che l'equazione di 2° grado per trovare a,b è la seguente:
che ha le due soluzioni:
quindi a=
, b=
e sostituiamo nella
, ottenendo:
ricordiamo adesso che , e che
, otteniamo (scrivendo poi Fn al posto di An) la formula in modo più compatto:
Applichiamo la formula per trovare il limite del rapporto: un quiz nella soluzione al quiz.
Usando tale formula, non è difficile dimostrare (ma nemmeno molto facile) che il limite dei rapporti è proprio :
si tenga conto del fatto che .
Vorrei che chi conosce i limiti provasse a dimostrarlo.
La formula di Binet ha una certa importanza perché consente di calcolare rapidamente, con l’ausilio di un calcolatore elettronico i numeri di Fibonacci corrispondenti a grandi valori di n evitando il calcolo dell’intera successione.
Altre proprietà geometriche della successione di Fibonacci QUI
QUI trovate tutti i quiz del Club dei Maghi







3 commenti
Direi che per n tendente a infinito il numeratore tende a Φn+1
e il denominatore tende a Φn
Dato che il limite di un rapporto equivale al rapporto dei limiti...
per n infinito avrò Φn+1 / Φn = Φ
ti ringrazio per la risposta sempre puntuale ma riusciresti a formalizzarla in qualche modo?con latex hai risolto?
Grazie a te, Umberto... ci provo con Latex
Al numeratore del rapporto scrivo il secondo termine si annulla, quindi resta
il secondo termine si annulla, quindi resta
numeratore =
Similmente al denominatore scrivo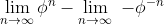 anche in questo caso il secondo termine si annulla
anche in questo caso il secondo termine si annulla
denominatore =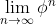
Il rapporto tra numeratore e denominatore è il limite cercato e vale