Categorie: Matematica
Tags: codibugnolo geometria Pappo Pippo quiz soluzione torta
Scritto da: Vincenzo Zappalà
Commenti:16
Quiz: la torta "codibugnolo" **
Ormai li conosciamo... Pippo e Pappo sono grandi mangiatori di torte. Il tempo è passato, ma le abitudini non sono cambiate. Ne consegue che Pippo propone quiz che sono facilmente risolvibili da un alunno delle scuole medie (di una volta almeno...). Questa volta abbiamo a che fare con una torta dalla forma molto strana che ricorda una passione di Pappo: i codibugnoli!
Nella Fig. 1 abbiamo la nostra torta, a cui sono state aggiunte delle decorazioni per farla assomigliare proprio al simpatico uccellino.
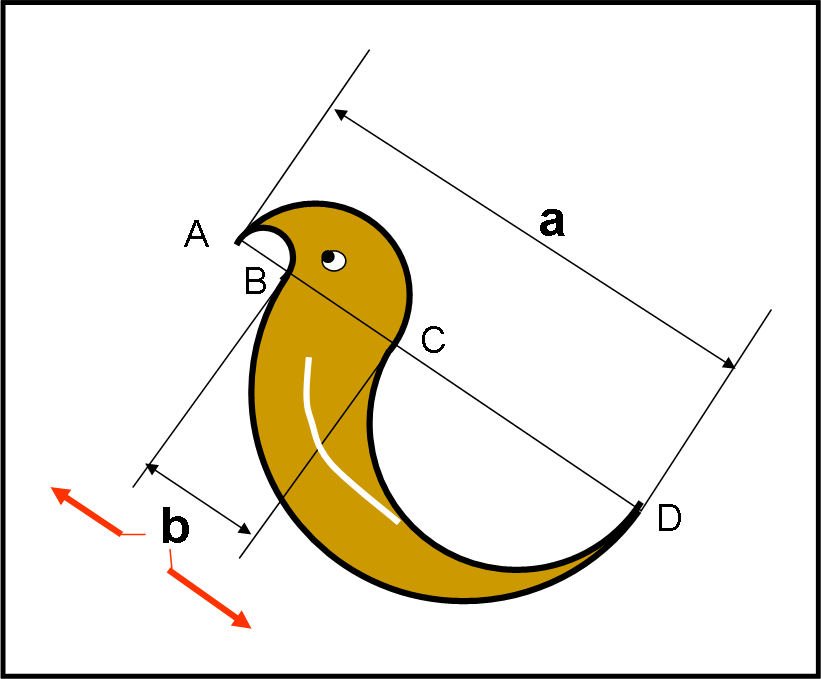
La domanda che fa Pippo è la seguente: "Caro Pappo, la torta deve avere delle misure fissate una volta per tutte e queste sono sia la lunghezza totale AD = a, che la parte sotto il musetto dell'uccellino, BC = b. Come vedi bene, la torta è delimitata da quattro semi circonferenze di diametro AB, AC, BD e CD. Tu puoi spostare il punto B (e di conseguenza il segmento BC che è fisso), lungo la direzione AD, ossia puoi accorciare o allungare il diametro AB. L'importante, ripeto ancora, è che AD non cambi e nemmeno BC. Se vuoi mangiare la torta devi dirmi per quale posizione del punto B la torta ha la massima area. Ovviamente, devi anche spiegarmi il perché..."
Vogliamo aiutare Pappo?
Come al solito vi è una soluzione abbastanza rapida e semplice, ma sono convinto che i nostri "maghi" (e non solo) sappiano sfruttare il problema per ricavarne una generalizzazione e chissà quali altre magie.
Chiedo, comunque, ai "maghi" di aspettare un paio di giorni prima di affrontare la nuova torta dei nostri amici.
Buon divertimento!
La risposta si trova direttamente nei commenti di Arturo, Jack e Maurizio...






16 commenti
Che bellina la torta "codibugnolo". Infatti la sua area resta sempre la stessa, pari a
per qualunque valore di AB , cioè comunque si sposti il segmento BC lungo AD
Naturalmente il valore indicato è il risultato di un ragionamento, che non ho scritto prima perché mi trovavo al lavoro e dovevo tornare a casa per pranzo...
L'area della torta tra A e C è data dalla differenza tra la semicirconferenza AC e la semicirconferenza AB. Analogamente, l'area della torta tra B e D è data dalla differenza tra la semicirconferenza BD e la semicirconferenza CD. Mettendo l'origine degli assi cartesiani in A, facendo coincidere l'asse x con la direzione AD, indicando quindi con x il segmento AB e trovando di conseguenza l'espressione analitica dell'area della torta in funzione di x, viene fuori che in tale espressione non è presente la x, ma eliminando i termini simili alla fine risulta proprio
A quel punto non c'è neanche bisogno di studiare la derivata della funzione per trovare il valore di x per cui si ha il valore massimo, perché, appunto, la funzione è costante.
il nostro grande Arturo aveva sparato subito la risposta... ma, ha poi letto il mio invito ad aspettare e l'ha cancellata, dando un chiaro segno di signorilità (che ben conoscevamo, comunque). Adesso, per ringraziarlo, cercate di dare la risposta!!
Ho appena ripristinato la risposta di Arturo... diamo a Cesare quel che è di Cesare...
QUIZ NEL QUIZ: trovare l'errore in questo rocambolesco tentativo di soluzione.
Ho cominciato a scarabocchiare qualcosa e ho partorito questa "genialata", secondo la quale l'area del codibugnolo sembra indipendente dalla lunghezza di b... sento una gran puzza di errore madornale, chi ha voglia di scovarlo?
Se fosse indipendente da b, vorrebbe dire che potresti ingrandire il collo del codibugnolo a piacere (restando fisso a) e avresti sempre la stessa area.... mmmmh....
E infatti è per questo che sono sicura che la soluzione sia sbagliata
Inoltre non è vero che non dipende da b, dato che c e d dipendono da b (oltre che da a). b non si vede, ma c'è!
Torta codibugnolo
Farina, uova fresche, zucchero, burro e poco altro, lievitato per ore. Poi in forno a legna.
Sono ricordi di un bambino di 10 anni che viveva in campagna.
Sembra di sentire ancora il calore del fuoco di Aprile, e le fatiche dei mesi di Gennaio e Febbraio per raccogliere i rami ai piedi dei filari potati.
Filari con la vite di campagna e piante che sostituiscono i pali secchi delle viti di collina a dividere campi di frumento e di trifoglio.
Le corse con il trattore per raccogliere il fieno prima della pioggia.
Maggio i bambini (piccoli adulti), tagliavano l'erba per il fieno, fermando, ogni tanto, il trattore vicino alle piante per ripararsi all'ombra e talvolta si saliva sulle ruote e si curiosava tra i rami.
Non esisteva internet, e si doveva chiedere al nonno, che spiegava del "galeto magiarolo" (visto uno la settimana scorsa).
Mentre ora non esistono più i filari, U GRINTU, Clinton o Grintòn.
Forse tornano con CRISPR?
grazie Gianfranco per regalarci i tuoi cari ricordi...
Facendo riferimento al disegno di Daniela
AC1=π (b+d)2/8
AC2=πd2/8;
AC3=π (a-d)2/8
AC4=π(a-(b+d))2/8
Atot=AC1-AC2+AC3-AC4
-1/8 π (a-b-d)2+1/8 π (a-d)2+1/8 π(b+d)2-πd2/8=abπ/4
Essendo a e b dati l'area totale è costante e non dipende da d e quindi
dalla posizione del punto B
caro Jack,
potresti esplicitare meglio i vari passaggi? grazie!
Facendo riferimento al disegno di Daniela
AC1=1/8 π(b+d)^2
AC2=1/8πd^2
AC3=1/8π(a-d)^2
AC4=1/8π(a-b-d)^2
Atot=AC1-AC2+AC3-AC4
1/8 π(b+d)^2-1/8πd^2+1/8π(a-d)^2-1/8π(a-b-d)^2=
1/8π(b^2+d^2+2bd-d^2+a^2-2ad+d^2-a^2 + 2 a b - b^2 +2 a d - 2 b d - d^2)=
2abπ/8=
πab/4
Essendo a e b dati ,l'area totale è costante e non dipende da d e quindi
dalla posizione del punto B
grazie Jack...
aspettiamo qualche altra risposta...
Una banale osservazione a margine, diciamo una "curiosità"....
Grazie alla dimostrazione di Jack sappiamo che l'area della torta è costante per qualsiasi spostamento del segmento b. In particolare questa area è l'area di un cerchio il cui diametro è la media geometrica di "a" e "b"
Infatti πab/4 può essere scritto π (√ab /2)2
Ma come viene mantenuta costante questa area , allo spostarsi del segmento "b"? Certamente le due parti della figura (sopra e sotto la linea orizzontale lungo la quale si muove b) ad ogni spostamento di b cambieranno forma, ma cosa possiamo dire delle loro aree? Restano costanti ambedue?
Osserviamo questa animazione (fatta "alla buona" solo per capire)
La prima sensazione che ne possiamo trarre è che, mentre un'area aumenta, l'altra diminuisce. Allora se il totale deve restare immutato significa che abbiamo una "trasfusione" di area da una zona all'altra: tanto aumenta l'una , tanto diminuisce l'altra.
Non ci resta che verificare questa affermazione ....
Nella figura sono indicati i vari diametri e il segmento b. Immaginiamo che b venga fato scorrere verso destra di una quantità "s". Scriviamo ora la variazione della area superiore (che verrà espansa) come differenza tra valore iniziale e finale:
delta area superiore = π/8 [ (D1 + s )2 - (D2 +s)2 ] - π/8 (D12- D22) sviluppando, otteniamo:
π/8 ( D12 + 2D1s + s2 - D22 - 2D2s - s2 - D12 - D22) e semplificando...
= π/4 s(D1-D2) = π/4 sb.
Allo stesso modo possiamo calcolare la variazione che subirà l'area inferiore (che verrà compressa):
delta area inferiore = π/8 [ (D3 - s )2 - (D4 -s)2 ] - π/8 (D32- D42) sviluppando, otteniamo:
π/8 ( D32 - 2D3s + s2 - D42 + 2D4s - s2 - D32 + D42) e semplificando...
=-π/4 s(D4-D3) = - π/4 sb.
Risultato che conferma la costanza dell'area complessiva per qualsiasi posizionamento del segmento b.
La struttura di questa formula è identica a quella del risultato trovato da Jack per l'area totale, anche l'area "scambiata" è quella di un cerchio il cui diametro, questa volta, è la media geometrica di "s" e "b".
Bravo Jack e bravo , ovviamente, Maurizio per aver generalizzato il succo della "torta". A loro aggiungo anche Arturo che era arrivato rapido come un fulmine quasi prima che pubblicassi il quiz . Sono sicuro che anche altri ci sarebbero arrivati e c'arriveranno. Come sempre a loro consiglio di NON LEGGERE I COMMENTI e proseguire comunque...
. Sono sicuro che anche altri ci sarebbero arrivati e c'arriveranno. Come sempre a loro consiglio di NON LEGGERE I COMMENTI e proseguire comunque...
Per i più bravi sto preparando un quiz decisamente più complicato (forse... dato che siete dei veri mghi).
Un grazie e un bravo particolare, ripeto, va a Jack che spero abbia rotto il ghiaccio e si scateni d'ora in poi...
Dato che oggi non si riesce ad usare Latex, mi ero affidato alla formattazione del testo per indicare gli esponenti come apici. Ma vedo che nella pubblicazione questa formattazione va persa. Riscrivo allora con una notazione diversa le formule per renderle un po' più comprensibili ......
delta area superiore = π/8 [ (D1 + s )^2 - (D2 +s)^2 ] - π/8 (D1^2- D2^2) sviluppando, otteniamo:
π/8 ( D1^2 + 2D1s + s^2 - D2^2 - 2D2s - s^2 - D1^2 + D2^2) e semplificando...
= π/4 s(D1-D2) = π/4 sb.
Allo stesso modo possiamo calcolare la variazione che subirà l'area inferiore (che verrà compressa):
delta area inferiore = π/8 [ (D3 - s )^2 - (D4 -s)^2 ] - π/8 (D3^2- D4^2) sviluppando, otteniamo:
π/8 ( D3^2 - 2D3s + s^2 - D4^2 + 2D4s - s^2 - D3^2 + D4^2) e semplificando...
=-π/4 s(D4-D3) = - π/4 sb.