Categorie: Meccanica Celeste Pianeti Sole
Tags: astrometria atmosfera Venere distanza del Sole goccia nera Halley Le Gentil parallasse solare transito Venere
Scritto da: Vincenzo Zappalà
Commenti:0
IL SOLE AMA IL NUMERO OTTO: LA STORIA DELLA DISTANZA DEL SOLE. 5 */**
Questa volta ci dedichiamo maggiormente all’avventura che non alla Scienza (a parte l’appendice dedicata al grande Halley): il transito di Venere del 1761.
Come già detto, negli anni successivi al 1672 ci furono solo tentativi più o meno riusciti di avvicinare o migliorare le osservazioni legate all’opposizione di Marte. Tuttavia, i limiti erano quelli che erano e c’erano poche speranze di far meglio di Cassini e Richer.
Un giovane scienziato, dal nome famosissimo, Halley, si convinse che il pianeta migliore per ottenere un vero miglioramento della parallasse solare fosse Venere. Se Horrocks era riuscito a seguire il transito sul Sole quasi miracolosamente -e genialmente-, il risultato sulla distanza era basato su ipotesi piuttosto fantasiose. Si poteva fare di più e impostare una nuova “base” per il calcolo della distanza del pianeta.
Lui stesso si era recato all’isola di Sant’Elena nel 1677 per assistere al transito di Mercurio, rendendosi conto che il piccolo pianeta non poteva fornire alcun valore accurato, ma che con Venere le cose sarebbero andate molto meglio. E’ facile capire perché: Mercurio è troppo vicino al Sole e la sua ombra, piccolissima, proiettata sul disco stellare, differirebbe angolarmente troppo poco tra due o più osservatori posti anche a grande distanza tra loro.
Si mise di buona lena a calcolare i transiti Venere futuri, fino al 2009. Nel contempo preparò un metodo per sfruttare queste configurazioni e determinare la parallasse solare (QUI una semplicissima spiegazione su cos'è la parallasse). In linea di principio, basterebbe eseguire le osservazioni da due luoghi molto distanti sulla Terra e assistere al transito del pianeta. Le due “linee” seguite da Venere sarebbero sufficientemente parallele e non sarebbe difficile misurare la distanza tra di loro. Un semplice schema geometrico permetterebbe di ottenere la distanza di Venere in chilometri e quindi, come al solito, arrivare a quella del Sole attraverso le leggi di Keplero.
Anche se non ce ne sarebbe più bisogno, riportiamo lo schema semplificato in Fig. 17. Due punti P e P’ sulla Terra vedono le tracce AA’ e BB’ di Venere sul Sole. La differenza angolare tra le due tracce dona l’angolo parallattico da cui si arriva velocemente alla distanza d. Bastava riportare i tempi di un certo contatto, presi da due osservatori diversi.
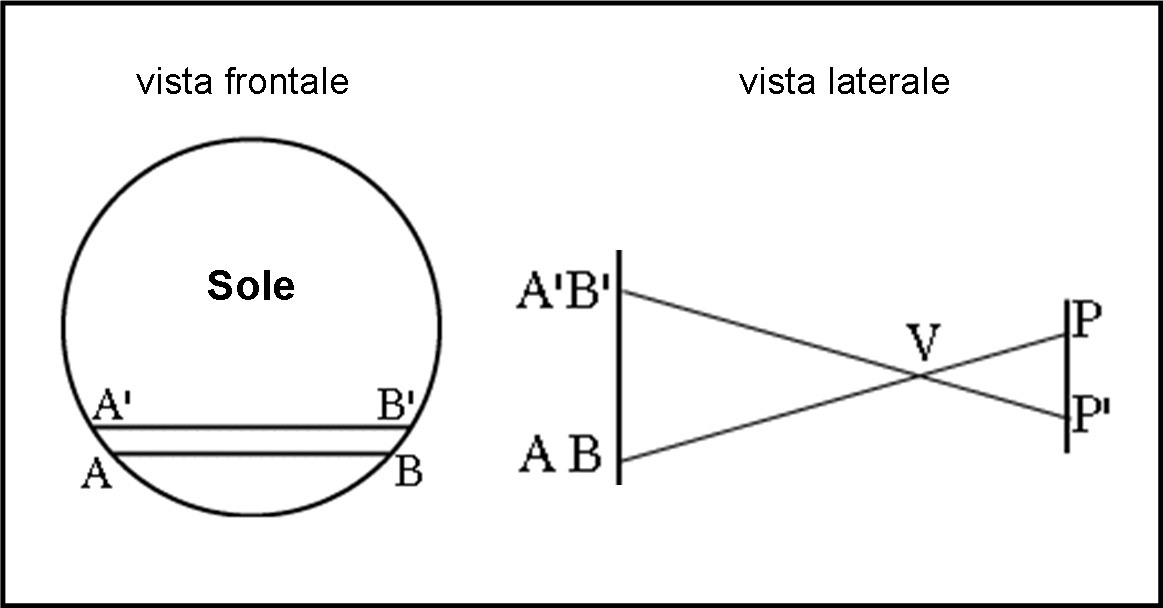
Questo voleva dire, però, sincronizzare gli orologi, conoscere perfettamente le coordinate dei luoghi di osservazione, ben sapendo che la distanza tra le due tracce del pianeta sarebbero state estremamente vicine e l’angolo sotteso da terra estremamente piccolo. Anche disperdendosi sul pianeta Terra le linee sarebbero state estremamente simili tra loro, più vicine dello stesso diametro apparente di Venere (vedi Fig. 18, relativa proprio a tre osservazioni del 1761).
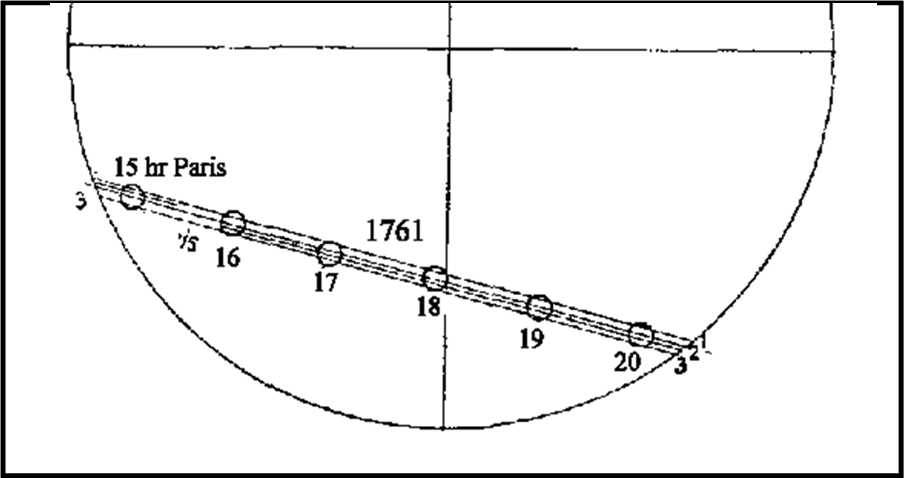
Ideò, perciò, un metodo più complesso, ma sicuramente più vantaggioso: ottenere la differenza tra due corde attraverso la durata dei transiti. Ovviamente più osservatori ci fossero stati, dispersi un po’ ovunque nella zona di visibilità, migliore sarebbe stato il risultato finale. Il metodo si basava su tempi locali (intervalli di tempo) e non necessitava di sincronizzazione di orologi, così come non era troppo sensibile all’esattezza delle coordinate. Teniamo conto che le durate dei transiti sono dell’ordine di molte ore. L’errore sulla distanza tra le due tracce sarebbe stato ben piccolo potendo misurare intervalli molto lunghi senza doverli legare temporalmente tra loro.
Halley era convinto di trovare la parallasse solare con un errore piccolissimo, cosa che in realtà era troppo ottimistica sia per motivi logistici e tecnici, sia per la celebre “goccia nera”, che ancora oggi rimane un fenomeno non del tutto risolto (ne parleremo la prossima puntata). Tuttavia, è quasi commovente leggere le parole di Halley, con le quali invita tutti gli scienziati ad agire e a prepararsi, anche a costo di viaggi in zone remote della durata di anni, per determinare il “metro” ufficiale del nostro Sistema Solare. Un grido per il bene della Scienza, dato che lui non avrebbe potuto partecipare al fantastico appuntamento. In effetti, morì vent’anni prima dell’agognato transito. E non fu questo il suo unico grido per il bene della Scienza... pochi sanno che fu grazie alla sua insistenza e al suo finanziamento se Newton si decise a pubblicare, sedici anni dopo averlo scritto, il suo libro più famoso “Philosophiae Naturalis Principia Mathematica", nel quale è formalizzata la Legge di Gravitazione Universale (Newton "in persona" lo ha raccontato ad Astericcio & co. QUI).
Vale la pena riportare in Appendice, in modo semplificato, il metodo usato da Halley, ricordando prima una sua ulteriore intuizione relativa all’ottenimento della più lunga durata possibile del transito, che avrebbe aumentato la precisione del risultato (complicando un po' i calcoli).
Utilizziamo qualche semplice figura per visualizzare l’idea di base. Durante il transito che comanda l’intera faccenda è il moto relativo di Venere rispetto a quello della Terra. Il primo, per la terza legge di Keplero, si muove più velocemente e quindi insegue, raggiunge e supera la Terra. Tuttavia, dobbiamo anche considerare la rotazione della Terra…
La Fig. 19 riporta la situazione generalizzata (ricordiamo che il transito avviene quando Venere e Terra si trovano vicinissimi alla linea dei nodi dell’orbita venusiana). Conoscendo i periodi e la rotazione terrestre non è un problema valutare il moto relativo sul Sole del disco venusiano.

Immaginiamo, per un attimo, che la terra (azzurra) sia ferma e non ruoti attorno al suo asse. La durata del transito dipenderebbe solo e soltanto dal moto orbitale di Venere. Mettiamo in moto anche la Terra, ma senza rotazione: la durata del transito dipenderebbe adesso solo dalla differenza di moto tra i due pianeti. Inseriamo, infine, anche la rotazione dalla Terra. Cosa succede alla durata del transito?
L’emisfero che vede il Sole si muove in senso opposto al moto orbitale di Venere, diminuendo, perciò, la durata totale: Venere scappa in avanti ancora più velocemente. Sarebbe, invece, molto bello ottenere un transito più lungo, non solo a causa della posizione relativa dell’osservatore sull’emisfero illuminato dal Sole, ma anche sfruttando il moto della Terra…
Prendiamo un osservatore che stia nell’emisfero buio. Il suo moto a causa della rotazione terrestre andrebbe nello stesso senso di quello orbitale di Venere. Venere scapperebbe in avanti, ma l’Osservatore utilizzerebbe la rotazione per starle dietro e ritardare la fine del transito!
Una durata più lunga sarebbe utilissima per Halley e per la riduzione dell’errore. Sì, bellissimo… ma l’osservatore sarebbe nell’emisfero notturno ed è ben noto che di notte NON si vede il Sole! Attenzione… ciò sarebbe un ostacolo insormontabile se e soltanto se la Terra ruotasse attorno a un asse perpendicolare al suo piano orbitale, che è estremamente simile a quello di Venere. In realtà l’eclittica forma un angolo di 23° con l’equatore e se si andasse abbastanza a nord (o a sud) si potrebbe assistere all’ingresso e all’uscita di Venere dal disco solare, proprio come mostra la Fig. 20.
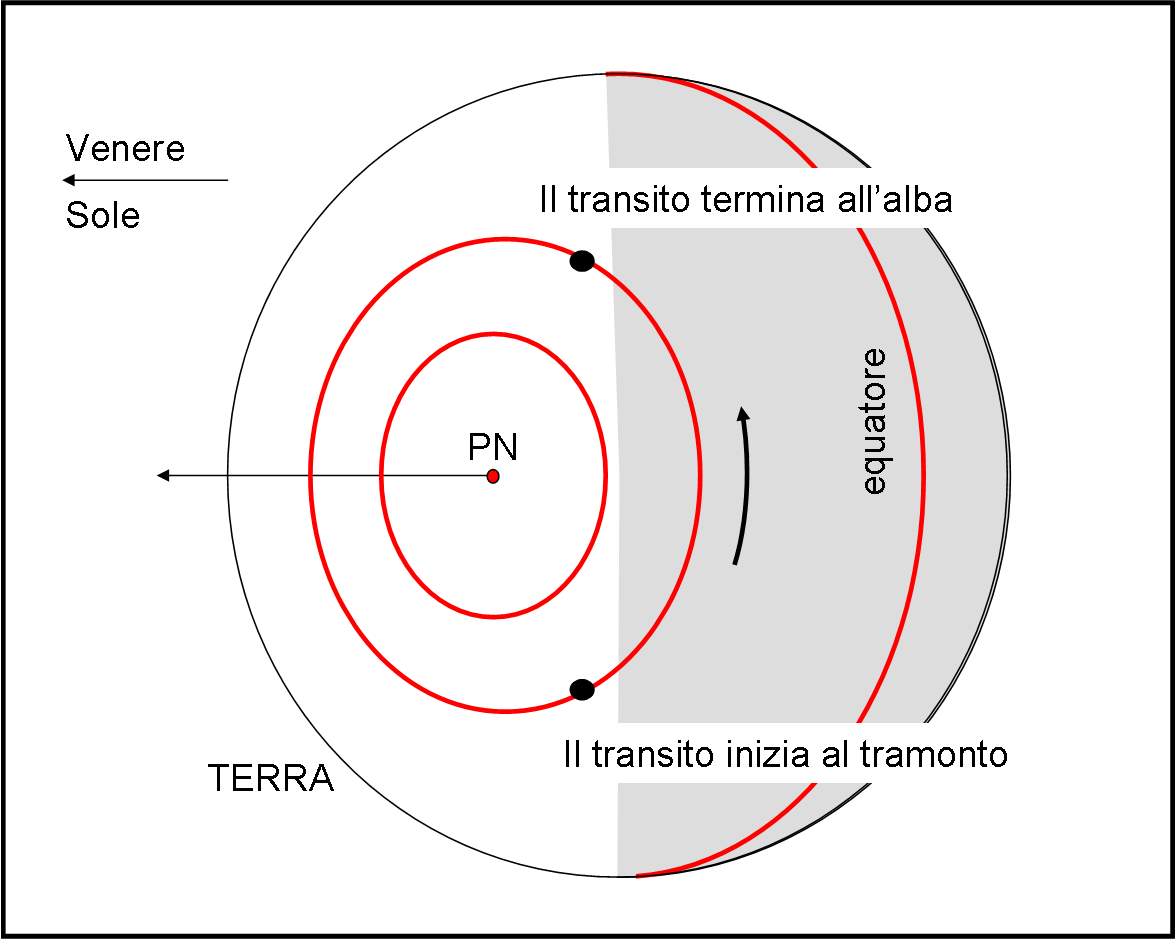
La Terra è vista dal polo nord dell’eclittica mentre un osservatore P descrive un cerchio attorno al Polo Nord. Se è abbastanza a nord potrebbe vedere l’inizio del transito al tramonto, andare a farsi un bel pisolino, e alzarsi in tempo per assistere alla fine del transito, la mattina successiva. Questo tipo di osservazione quasi-notturna permetterebbe una durata più lunga di quella solamente diurna… Ovviamente la latitudine andrebbe scelta con cura, dato che se troppo vicina al polo, il moto dovuto alla rotazione sarebbe minimo.
Il mondo di allora non era certo quello di oggi (beh… almeno quello di ieri) e spostarsi in luoghi remoti e conoscerne le coordinate geografiche era un problema non da poco, che abbisognava di molto coraggio e lunghi tempi di preparazione. Halley aveva cercato di limitarli, ma le sue previsioni e il suo metodo vennero criticati negli anni seguenti e quando ci si avvicinò alla data fatidica si cominciò a preparare la rete osservativa basandosi soprattutto sulla sfida delle capacità e delle convinzioni di due grandi potenze, Francia e Inghilterra. Oltre a una rivalità scientifica molto accentuata, bisogna tener conto che Francia e Inghilterra erano in guerra (guerra dei sette anni) e spostarsi o attraversare colonie di una o dell’altra nazione non era facile, anche se gli scienziati partecipanti all’evento avevano ottenuto uno speciale, ma traballante, lasciapassare.
Purtroppo, le previsioni fatte da Halley sui luoghi di visibilità risultarono non esatte, forse per un errore di calcolo o forse a causa della poca accuratezza dei dati utilizzati. Fatto sta che un francese, Delisle, oltre a fornire un utilissimo mappamondo (Fig. 21) a coloro che erano pronti per il viaggio, propose un metodo diverso da quello di Halley, che, pur tenendo conto delle sue intuizioni, si basava nuovamente anche sui tempi assoluti di entrata e di uscita, in punti limite della sfera terrestre.

Ovviamente, per potere tracciare le linee di visibilità bisognava imporre una certa distanza del Sole ed egli scelse quella corrispondente a una parallasse solare di 10”, invece che di 8.8”. Ciò comportava un notevole rischio che i luoghi limite potessero anche essere al di fuori della zona di visibilità. In ogni modo, la comunità scientifica si scatenò dando vita a spedizioni estremamente rocambolesche.
Le difficoltà logistiche e tecniche (gli orologi erano quelli che erano), i tempi lunghissimi di preparazione, le rivalità tra scienziati, la guerra in corso e gli ovvi errori di previsione che ancora rimanevano, fecero sì che le spedizioni del 1761 non portarono a risultati veramente brillanti e si ottennero valori spesso discordanti tra loro (da 8.3” a 10.6” secondi d’arco per la parallasse solare). Senza parlare, poi, dell’imprevista apparizione della goccia nera (black drop) al momento del contatto interno (Fig. 22). In quel contesto, il maggiore interesse sta, forse, nelle avventure degli astronomi dispersi per il mondo.


Potremmo anche chiederci: “Ma queste spedizioni dovevano costare molti soldi e l’interesse scientifico era piuttosto ristretto, in epoche di guerre e di conquiste. Come si riuscirono a mettere in piedi spedizioni così lunghe e costose?” La realtà è che la politica favorì le esplorazioni in luoghi remoti che avrebbero potuto avere un qualche interesse coloniale e/o commerciale. Gli scienziati furono usati come veri e propri ambasciatori in vista di ripercussioni che di scientifico avevano ben poco. Tuttavia, con tutti problemi e gli scontri di pensiero, il transito di Venere del 1761 diede il via alla prima vera e propria collaborazione internazionale nella storia dell’Astronomia. Come già detto le Nazioni più coinvolte furono Inghilterra e Francia, per le spedizioni più lontane, la prima legata ad Halley e la seconda a Delisle. Tuttavia, si lavorò assiduamente anche in Europa,
L’accademia di Parigi finanziò due spedizioni, una all’isola di Rodrigue, una colonia nell’Oceano Indiano (arcipelago delle Mascarene), e l’altra a Pondicherry in India. Un altro accademico francese, su invito dell’Accademia di S. Pietroburgo, si recò in Siberia, dove il transito sarebbe stato interamente visibile.
La Royal Society inglese, in un primo tempo, pensò di organizzare una spedizione alla Baia di Hudson nell’America Settentrionale, località consigliata da Halley, fino ad allora ritenuto uno dei siti più favorevoli per l’osservazione del transito. Tuttavia, i piani cambiarono quando Delisle dimostrò che Halley aveva indicato una zona molto probabilmente esterna alla visibilità del transito. Si ripiegò, perciò, sull’isola di Sant’Elena, nell’Oceano Atlantico, e verso l’isola di Sumatra, mai raggiunta, che venne sostituita col Capo di Buona Speranza.
In particolare, una nota speciale meritano sia l’inviato in Siberia (Chappe) che Guillaume Le Gentil, che partì nel 1759 per recarsi a Pondicherry.
La meta dell’abate Chappe era Tobolsk, città siberiana a 400 chilometri a est degli Urali. Possiamo immaginare il suo viaggio e il suo arrivo, durante l’inverno, in un posto a quasi 6000 chilometri da Parigi. Coraggioso è dir poco. Chappe partì da Parigi nel novembre 1760, portando con sé un mucchio di strumenti, un servitore personale e un orologiaio di fiducia. Dopo un viaggio molto avventuroso, finalmente, il 10 aprile del 1761 arrivò a Tobolsk.
La notte prima del transito era molto nuvolosa e molto fredda. Chappe, rintanato nel suo osservatorio di fortuna, vedeva solo nuvole e sentiva un vento impetuoso. Fu proprio quest’ultimo a salvarlo, ripulendo il cielo verso le 7 del mattino. Il Sole apparve quando già il primo contatto esterno era avvenuto e, quando il pianeta non era ancora completamente entrato sul Sole. Tanta fatica, ma anche tanta fortuna.
Ben più triste l’avventura di Guillaume Le Gentil.
Egli partì dalla Francia il 26 marzo del 1760 per recarsi in India. La prima tappa era l’isola Mauritius (allora colonia francese). Dopo aver circumnavigato l’Africa egli giunse nell’isola il 10 luglio del 1760, decisamente in tempo per arrivare alla destinazione finale di Pondicherry. Tuttavia, sorsero infinite e inattese complicazione per recuperare la fregata necessaria alla traversata verso l’India. Riuscì a partire solo l’11 maggio del 1761. Dopo una breve sosta all’Isola della Reunion, comparve una bonaccia spaventosa che costrinse la nave a procedere lentamente lungo la costa africana.
Infine, il 24 maggio (12 giorni soltanto prima dell’evento tanto agognato) la fregata si fermò nel distretto di Mahe, in India, dove si venne a sapere che gli inglesi avevano conquistato con la forza la città di Pondicherry. Il capitano decise di raggiungere un porto di Ceylon, Point de Galle, dove la vittoria degli inglesi venne confermata. Niente da fare, si doveva tornare all’isola Mauritius, solo sei giorni prima del transito di Venere. Nel mezzo dell’oceano, Le Gentil osservò con grande tristezza l’evento astronomico tanto atteso: il cielo era limpido, ma lui non aveva idea della esatta posizione del luogo e la fregata ballava su un mare non proprio tranquillo. Le misure effettuate dall’astronomo francese furono del tutto inutili.
Il 23 giugno la nave entrò nel porto di Mauritius (il viaggio è descritto in Fig. 23).
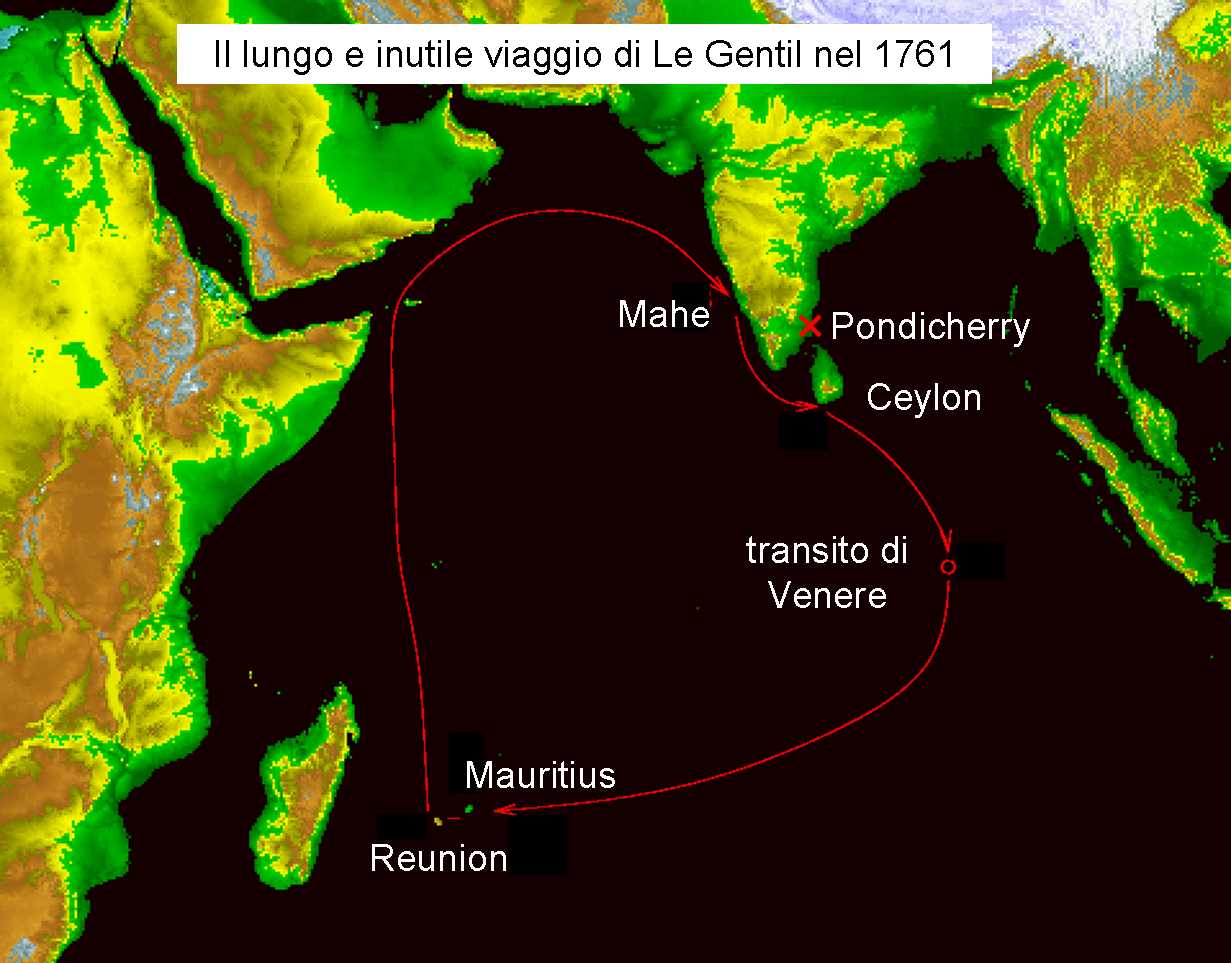
Non restava che tornare, deluso e scoraggiato, in Francia. Le Gentil, però, prese un’altra decisione… il prossimo transito di Venere sarebbe stato “solo” otto anni più tardi, il 3 giugno del 1769. Perché non aspettare? E così fece, scorrazzando per l’Oceano Pacifico ed eseguendo studi di ogni tipo. Sul suo diario scrisse: “Feci tutte le osservazioni possibili di geografia, storia naturale, fisica, astronomia, navigazione, venti e marea…”
Passati gli otto anni, si preparò a raggiungere Pondicherry, la base delle sue operazioni, dove arrivò in netto anticipo, a fine marzo del 1768. Il governatore fu estremamente gentile e gli diede tutto l’appoggio possibile. Le Gentil scelse come residenza un palazzo che era stato distrutto dalla guerra e iniziò a calcolare la latitudine e la longitudine del luogo con la precisione richiesta. Per tutto il mese di maggio il cielo mattutino fu sereno così come i primi due giorni di giugno.
Improvvisamente, l’ultima notte, il tempo cambiò drasticamente. Durante tutto il transito, il Sole venne oscurato da nubi minacciose, ma si fece rivedere due ore dopo la fine del transito: Le Gentil aveva fallito nuovamente! Egli scrisse nel suo diario: “Questo è il destino di molti astronomi. Mi sembra ancora impossibile aver percorso 70 000 miglia, lontano da casa, per assistere a un passaggio ininterrotto di nuvole. Non riesco ancora a crederci e faccio fatica a scrivere…”.
Ci vollero altri due anni per vedere il ritorno di Le Gentil nella sua terra, dove, nel frattempo, la sua casa era stata completamente svaligiata e la sua proprietà saccheggiata dagli avidi parenti che lo avevano creduto morto. Inoltre, per non farsi mancare niente, seppe anche che il suo posto presso l’Accademia era stato assegnato ad un collega.
Una storia triste che non merita commenti ulteriori…
La deludente campagna osservativa del 1761 ottenne però due importanti risultati. L’astronomo russo Mikhail V. Lomonosov , si accorse del bordo luminoso di Venere (tutti si aspettavano un dischetto nero) e capì che il pianeta doveva possedere un’atmosfera. A Parigi, il celebre Josephe-Jerome de Lalande illustrò accuratamente la goccia nera durante il contatto interno.
Appendice: Il metodo di Halley
Ci basta la semplice Fig. 24.
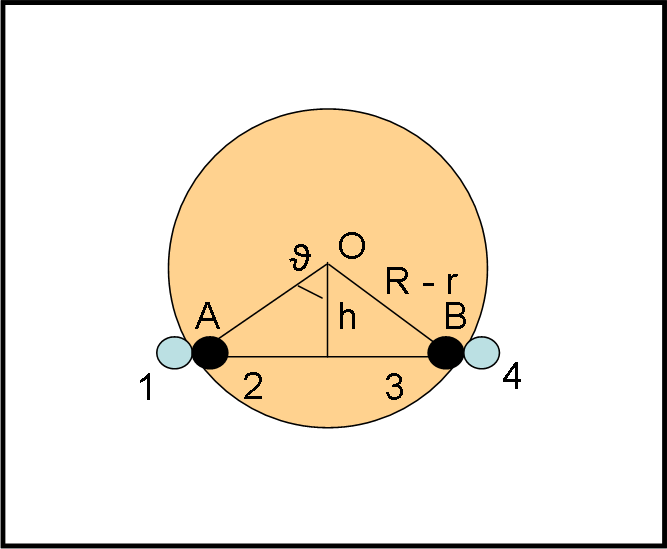
Innanzitutto vanno scelti gli istanti più opportuni per misurare la lunghezza temporale del transito. Non vi è molta scelta: il secondo e il terzo contatto interno, in quanto quelli esterni si vedrebbero solo a transito iniziato. I raggi R e r dei corpi celesti coinvolti sono di circa 31’ (il Sole) e di 1’ (Venere). Quello di Venere non può essere trascurato e quindi i contatti vengono considerati relativi al centro del dischetto nero di Venere. Essi stanno perciò su un cerchio di raggio R – r. In pratica è come se il transito avvenisse lungo una corda di un disco di raggio “ridotto” pari a 31’ – 0.5’ = 30.5’.
Abbiamo subito che:
h = (R - r) cos ϑ …. (1)
Tuttavia, possiamo anche scrivere che il tempo di durata è legato alla lunghezza AB, ossia:
T = k∙AB
Il coefficiente k non pone nessun problema, dato che lo scopo è quello di misurare differenze di durata tra due osservatori e, quindi, alla fine si semplificherà. Ricordiamo che stiamo considerando un caso standard, con osservazioni diurne e, quindi, con moti relativi uguali.
Dalla Fig. 1, si ha anche:
T = 2k (R - r) sen ϑ …. (2)
Immaginiamo, adesso, che in un’altra località la corda ottenuta sia più lunga. Il che vuol dire che invece di un angolo ϑ si deve considerare un angolo ϑ + δ, con δ molto piccolo.
Da cui:
h’ = (R - r) cos (ϑ + δ) = (R – r) (cos ϑ cos δ - sen ϑ sen δ)
L’angolo δ è molto piccolo e tale è anche il suo seno. Tuttavia, non si può escluderlo nel calcolo, mentre il coseno è talmente vicino a 1 che può essere sostituito dall’unità. Per dimostralo basta ricordare che l’approssimazione del coseno va con il seno al quadrato e quindi può essere tranquillamente sostituito con 1, equivalendo a escludere i termini di secondo grado nel seno.
Possiamo, perciò scrivere:
h’ = (R – r) (cos ϑ - sen ϑ sen δ) …. (3)
Facendo la differenza tra la (3) e la (1), si ha:
h’ – h = (R – r) (cos ϑ - sen ϑ sen δ) - (R - r) cos ϑ = - (R – r) sen ϑ sen δ
D = h – h’ = (R – r) sen ϑ sen δ …. (4)
Consideriamo la (2), la sua analoga relativa al secondo osservatore è:
T’ = 2k (R - r) sen (ϑ + δ) = 2k (R– r)(sin ϑ cos δ + cos ϑ sin δ)
Approssimando come prima:
T’ = 2k (R– r)(sin ϑ + cos ϑ sin δ)
Ma, ricordando la (2):
T’ = T + 2k (R– r) cos ϑ sin δ
T’ - T = ΔT = 2k (R– r) cos ϑ sin δ
E, ancora:
ΔT/T = 2k (R– r) cos ϑ sin δ/(2k (R - r) sen ϑ) = cos ϑ sin δ/sen ϑ
Da cui si ricava, facilmente, sin δ:
sin δ = (sen ϑ/cos ϑ) ΔT/T
Sostituendo nella (4), si ha:
D = (R – r) sen ϑ sen δ = (R – r) sen ϑ (sen ϑ/cos ϑ) ΔT/T
D = (R – r) (sen2 ϑ/cos ϑ) ΔT/T …. (5)
Che è proprio quello che voleva Halley: determinare la distanza tra le corde attraverso la misura di tempi molto lunghi e non legati a un tempo assoluto.
Semplice, ma… geniale!
QUI la serie completa degli articoli dedicata alla storia del calcolo della distanza del Sole





