Continuiamo con la storia della determinazione della distanza del Sole, dopo la pausa introdotta con il quiz su Marte, che si rifaceva alla tecnica usata da Cassini. Il solo Paolo l’ha affrontato con grande accuratezza, facendomi pensare che questo argomento sia considerato, per molti, poco importante o interessante. Niente di più sbagliato. Non solo l’esatta determinazione della distanza Terra-Sole ha permesso di definire un’unità di misura fondamentale per qualsiasi approccio quantitativo al nostro Sistema Solare (l’Unità Astronomica), ma la lunga storia che l’accompagna permette di ripassare e di capire meglio tanti concetti relativi alla parallasse, ai transiti, alla trigonometria sferica e alle leggi di Keplero. Un consiglio? Rileggetevi le puntate precedenti e seguite quelle che usciranno. In alcuni casi ci sarà anche l’avventura portata a limiti estremi…

Torniamo, per un attimo, a Tycho Brahe che, a parte le sue idee a volte un po’ balzane e a volte geniali, è stato sicuramente un osservatore eccezionale, tanto che Keplero deve moltissimo a lui e alle sue osservazioni. Anche Tycho si era posto il problema della distanza dei pianeti, ma certo non per arrivare direttamente alla distanza del Sole, dato che le leggi di Keplero non erano ancora state stilate. Tycho tentò di misurare la distanza di Marte nel 1582, durante un’opposizione. L’idea era brillante, ma i mezzi non certo sufficienti…

La scelta dell’opposizione era essenziale: Marte si trovava a una distanza decisamente piccola (anche se non proprio nelle condizioni perfette come si ha quando, oltre che in opposizione, Marte è anche al perielio) ed era nelle condizioni migliori per potere misurare la sua parallasse. No, non spaventatevi, non aveva certo pensato di recarsi su Marte e vedere l’angolo che sottendeva la Terra. Poteva farlo anche da… casa.

L’idea (usata anche in seguito) sfruttava la rotazione della Terra attorno al proprio asse. Consideriamo la Fig. 9.

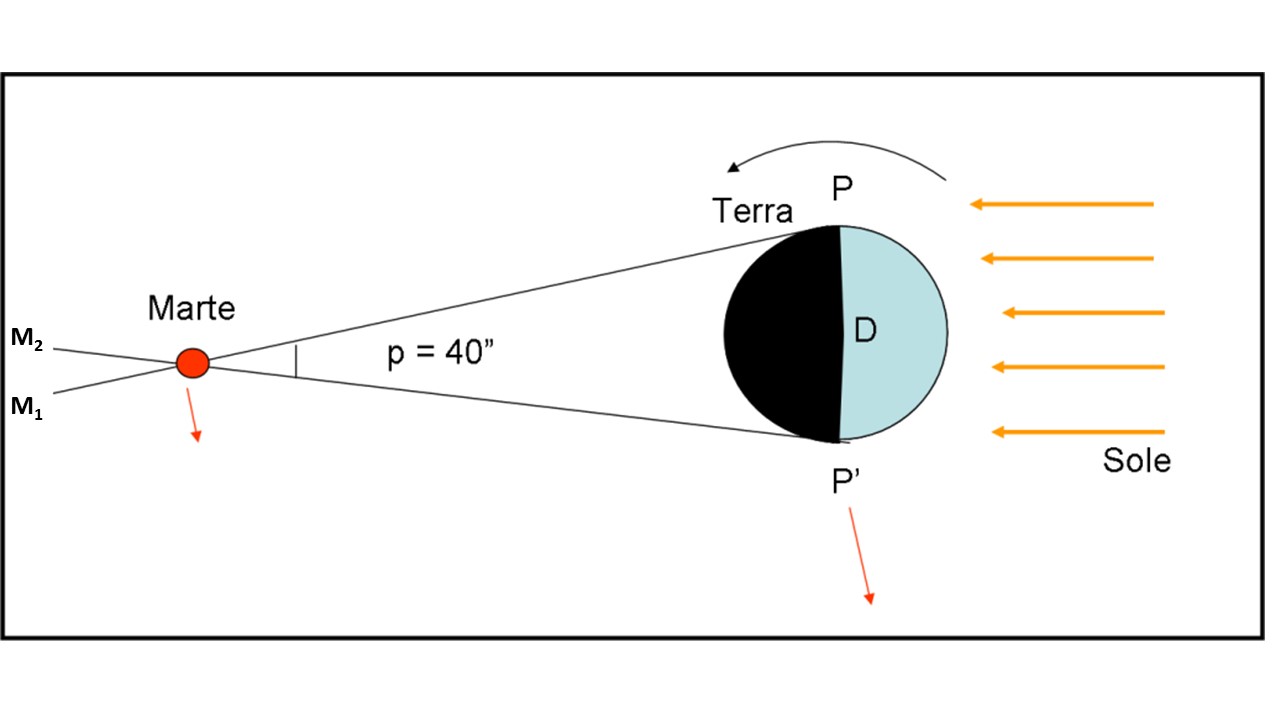
Siamo in opposizione e quindi Marte, la Terra  e il Sole  stanno lungo la stessa linea. L’osservatore osserva Marte in P, appena fa notte, e visualizza la sua posizione M₁ rispetto alle stelle vicine (che si possono considerare fisse). Poi aspetta che trascorra la notte e poco prima dell’alba, quando è in P’, osserva di nuovo Marte che ora si trova in M₂ rispetto alle stesse stelle di prima. La variazione angolare tra M₁ e M₂ è proprio l’angolo sotto cui Marte vede il diametro terrestre.

Geniale! Sì, ma solo teoricamente… Tycho non aveva telescopi a disposizione ed era impossibile per lui misurare un angolo che si aggira intorno ai 40”. Non solo, però… nel tempo che la Terra aveva compiuto mezza rotazione, si era anche spostata lungo la sua orbita, così come aveva fatto Marte. Spostamenti, questi, addirittura maggiori della parallasse di Marte. Per poterne tenere conto, avrebbe dovuto conoscere le orbite, ma questo ancora non era un dato acquisito! L’idea era buona, ma il risultato del tutto inconsistente.

Le cose diventarono molto diverse nel 1672, novant’anni dopo. Keplero aveva scritto le sue leggi e il telescopio era ormai uno strumento a portata di mano (anzi di occhio), con tanto di fili sottilissimi nell’oculare per effettuare misure molto precise. Inoltre Marte avrebbe avuto una grande opposizione, ossia sarebbe stata nel suo punto più vicino all’orbita terrestre. Si poteva provare e così fecero Cassini in Francia e Flamsteed in Inghilterra.

Muoviamo gli osservatori

Cominciamo con il primo, italiano verace, ma come al solito obbligato a espatriare per avere riconosciuti i suoi meriti; la sua idea era sempre quella di determinare la distanza di Marte per ricavare, dalle leggi di Keplero, quella del Sole.

Marte era all’opposizione a settembre, proprio vicinissima al perielio. Le condizioni erano ideali: distanza minima e, di conseguenza, angolo di parallasse massimo. Inoltre, Marte al perielio voleva dire notevoli semplificazioni nell’applicazione delle equazioni di Keplero (ricordiamo che Marte ha un’orbita eccentrica e questo era ben noto a Cassini). Per evitare il problema del movimento di Marte e della Terra, la cosa migliore era di creare un base per determinare la parallasse, in modo che le osservazioni ai due estremi venissero eseguite contemporaneamente. Potremmo chiamarla parallasse simultanea.

Il mondo era abbastanza ben conosciuto e la Francia aveva una colonia nell’America del Sud, in Guyana, dove era situata la città di La Caienna (La Cayenne, in francese) nei pressi dell’Isola del Diavolo, penitenziario tristemente famoso. La situazione politica, con gli inglesi soprattutto, non era del tutto tranquilla, ma Cassini decise di inviare in quel luogo molto distante dalla Francia un suo collaboratore, Richer.

Egli partì ben due anni prima, per calcolare perfettamente la posizione del luogo e per cercare di rendere il suo orologio (a pendolo) concorde con quello di Cassini. Un lavoro non da poco (Paolo nei suoi commenti ha mostrato buona parte di questi calcoli), che rese in qualche modo celebre Richer che, per primo, si accorse della differente gravità in due luoghi posti a differente latitudine. Ma torniamo alla nostra opposizione (Fig. 10) del 9 settembre 1672.

 

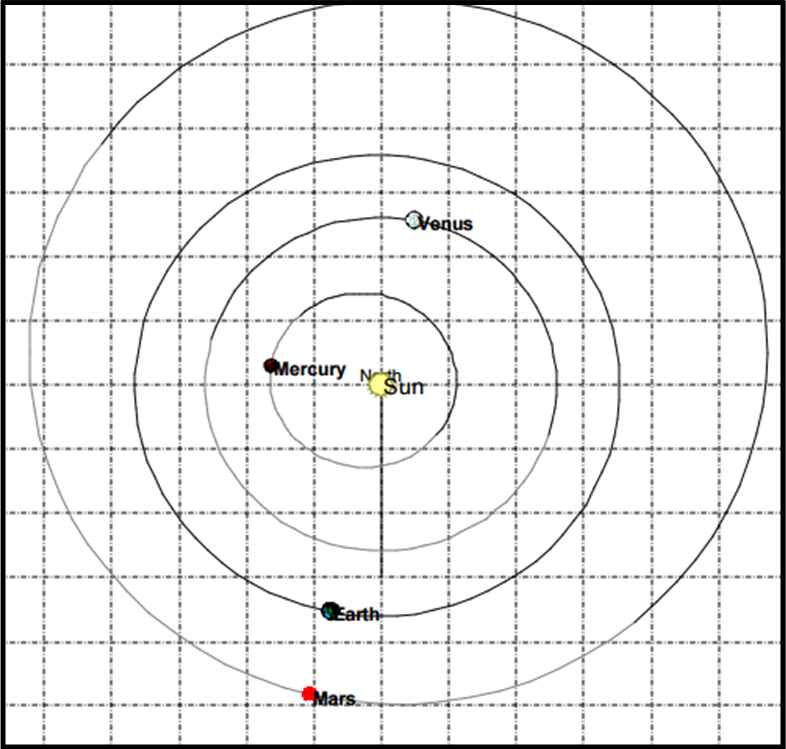
Tutto è pronto e la base D, ossia la distanza in linea retta tra Cassini e Richer, calcolata con la massima precisione possibile. All’ora stabilita entrambi eseguono la propria osservazione seguendo il procedimento visualizzato nella Fig. 11.

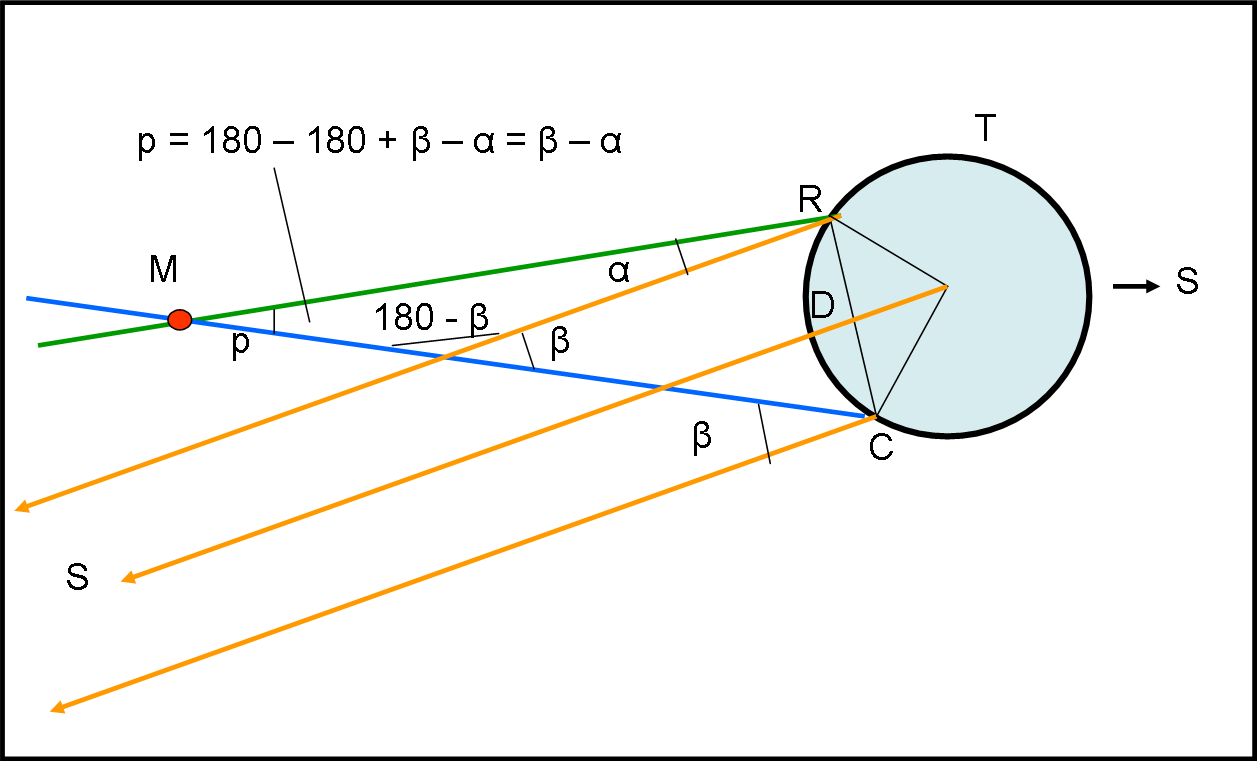
Ciò che i due osservatori, R e C, possono fare è misurare le diverse distanze angolari α e β tra Marte e una certa stella S di sfondo (in realtà, ne usano più di una). A quel punto, un minimo di calcoli sui triangoli coinvolti li porta alla determinazione della parallasse p, ossia dell’angolo sotto cui Marte vede la distanza D tra i due osservatori. L’angolo p risulta proprio uguale a β – α.

Non resta allora che passare al solito triangolo parallattico che ben conosciamo (Fig. 12 ).

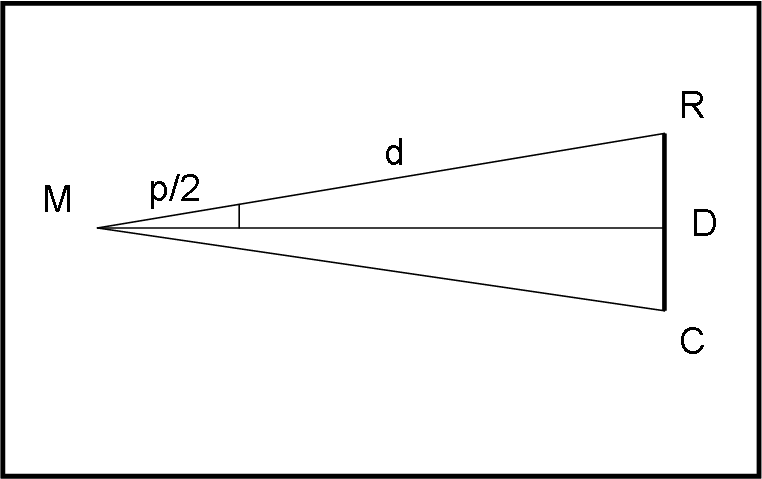
Non spaventiamoci se consideriamo rettangoli certi triangoli. Potremmo anche fare calcoli più precisi, ma vista la grandezza dell’angolo in gioco, le approssimazioni sono più che lecite, come quella di considerare il seno di un angolo uguale all’angolo stesso espresso in radianti. Alla fine si ottiene la ben nota relazione (che trovate QUI):

d sen (p/2) = D/2

d p/2 = D/2

d = D/p

Che permette di ricavare la distanza d, tra Marte e la Terra, in km o quello che si usava a quei tempi.

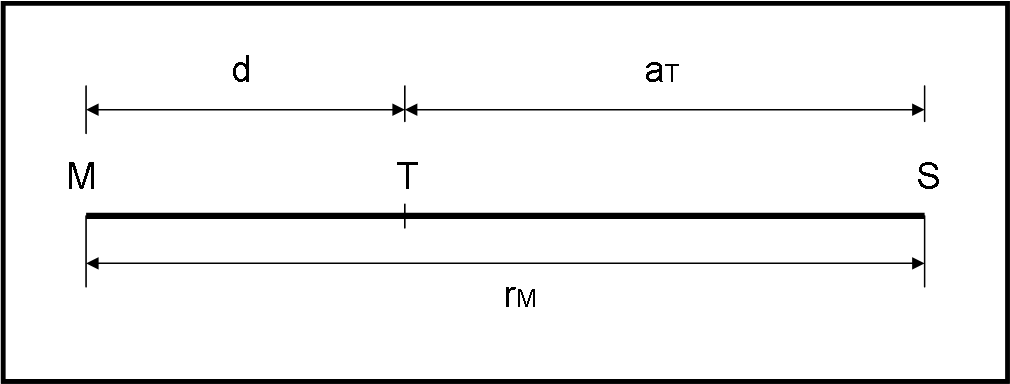
Restano, ancora, da applicare le leggi di Keplero, per ricavare la distanza a_T  tra la Terra e il Sole, tenendo presente che Marte si trova al perielio della sua orbita (Fig. 13).

Cassini conosce i periodi dei due pianeti e può tranquillamente applicare la terza legge di Keplero (considerando l’orbita della Terra circolare, ossia a_T = costante):

a_M³/a_T³= P_M²/P_T²

Sostituendo i valori noti dei periodi , ottiene il rapporto a_M/a_T

Cassini ha, però, calcolato la distanza d tra Marte e Terra al perielio di Marte e può scrivere (vedi Fig. 13):

d = r_M - a_T           ….  (2)

Sa, però, benissimo (dalla prima legge di Keplero) la relazione tra distanza perielica r_M  e il semiasse a_M (vedi QUI):

r_M = a_M (1 – e)

da cui (dividendo la (2) per a_T):

d/a_T = a_M (1 – e)/a_T  - 1   =  h (noto)

il secondo membro è una quantità nota dato a_M/a_T e l'eccentricità sono noti. Lo possiamo considerare una certa costante h, da cui:

a_T = d/h

Il che porta, inserendo i valori conosciuti a quei tempi, a una parallasse solare di 9”5 e a un valore dell’Unità Astronomica pari a 0.926 volte quella odierna (parallasse e distanza sono legati dal solito triangolo di Fig. 12). Un bel salto qualitativo, se escludiamo il colpo di fortuna di Huygens…

Per i più volenterosi:

Lo stesso risultato si può ottenere con una soluzione matematica, sicuramente più elaborata e abbastanza inutile. La propongo perché potrebbe servire da esercizio per chi vuole ripassare lo studio di funzioni…

Per la Terra si ha:

a_T³  = K P_T ²         …. (3)

per Marte, invece, ricordando che la distanza perielica r_M di Marte è uguale a

r_M = a_M (1 – e)      

si ha:

a_M³ = (r_M/(1 – e))³  = K P_M²         …. (4)

Dividendo la (4) per la (3) si ottiene:

(r_M³/((1 – e)³a_T³) = P_M²/P_T²

r_M³/a_T³ = (1 – e)³ P_M²/P_T²          …. (5)

Ma:

r_M = a_T + d

Il primo membro della (5) può scriversi:

((a_T + d)/a_T)³ = (1 + d/a_T)³

Ponendo

d/a_T = x

Si ha:

(1 + x)³ = 1 + x³ + 3x + 3x²

Da cui, la (5) diventa:

1 + x³ + 3x + 3x² = (1 – e)³ P_M²/P_T²

A questo punto possiamo inserire i valori numerici conosciuti e si ottiene:

x³ + 3x² + 3x = 1.6357

Una bella “cubica” completa che potrebbe risolversi per via numerica (con qualche difficoltà), ma che può anche risolversi per via grafica. Due soluzioni non sono reali e l’unica soluzione deve essere quella precedente… provate!

Lasciamo girare la Terra

In modo analogo a quanto tentato da Keplero, si muove, in Inghilterra, Flamsteed. Egli preferisce far tutto da solo, utilizzando un solo strumento ed evitando viaggi dispendiosi e spesso pericolosi. Inoltre c’è il problema degli orologi da sincronizzare. Si affida, perciò, alle osservazioni serali e mattutine per costruirsi la base parallattica. Ricordiamo che questo metodo prende il nome di parallasse diurna, sfruttando una base dipendente dal tempo trascorso durante una rotazione della Terra attorno al suo asse, così come la parallasse annua sfrutta una base dipendente dal tempo trascorso durante una rivoluzione della Terra attorno al Sole.

Tuttavia, deve tenere in conto il moto apparente di Marte rispetto alla Terra durante l’intervallo tra la prima e l’ultima osservazione. Un moto questo che comporterebbe di per sé un angolo maggiore di quello parallattico...

Il suo tentativo avviene ad ottobre, quando Marte si trova quasi esattamente nel punto in cui il suo moto passa da retrogrado a diretto (vedi Fig. 14).

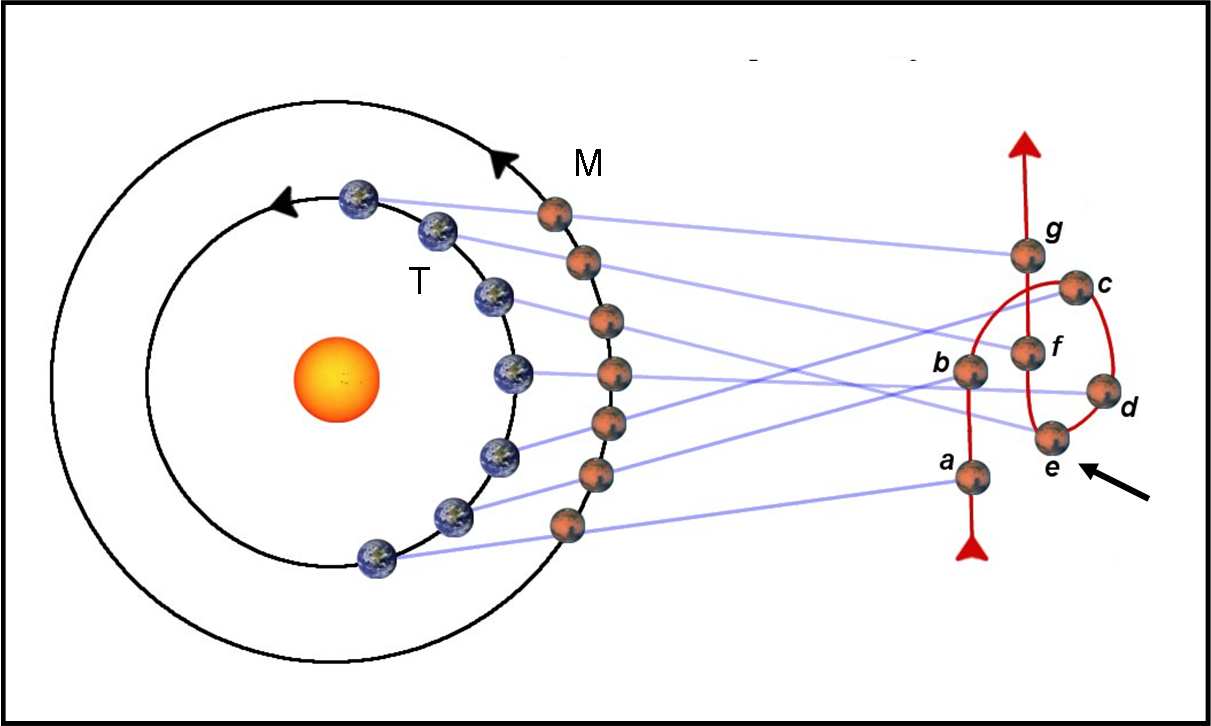
Non si sa se sia stata una scelta ponderata o un colpo di fortuna legato al fatto che in quella posizione vi erano molte stelle brillanti nei paraggi, ma sicuramente questo fatto lo ha aiutato non poco, riducendo praticamente a zero lo spostamento ϑ di Marte durante la notte.

La Fig. 15  riporta quanto eseguito da Flamsteed.

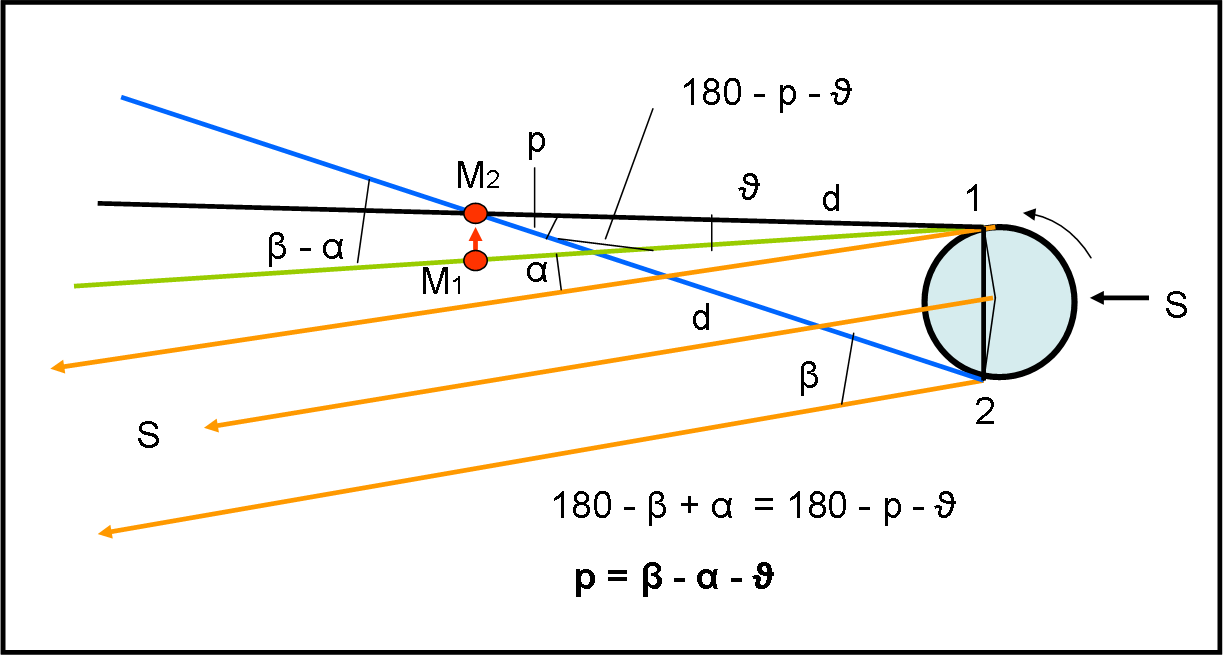
Alla fine ottiene, con poche e ovvie relazioni tra angoli di triangoli, l’angolo di parallasse p di Marte.

p = β - α - ϑ

Come già detto, la soluzione dipenderebbe dalla conoscenza dell’angolo ϑ, il cui calcolo non sarebbe un problema facile dato che supera il valore della stessa parallasse. La fortuna o la furbizia (io propendo per la seconda) fa sì, però, che questo angolo possa essere considerato uguale a zero, per cui Flamsteed ottiene facilmente p.

Il resto segue perfettamente quanto fatto da Cassini e il risultato finale non differisce di molto, trovando un valore della parallasse solare di 10” e un valore della Unità Astronomica pari a 0.879 volte quella odierna.

Due metodi e due risultati quasi uguali. Verrebbe da pensare che la comunità scientifica avrebbe dovuto essere convinta della validità del risultato. Invece, la situazione resta nel caos, dato che molti altri illustri studiosi e osservatori affrontano, in quegli anni, lo stesso problema ottenendo risultati completamente discordanti che portano a parallassi solari che variano da 29” a 6”. Lo stesso Newton si dimostra estremamente scettico verso i risultati di Cassini e Flamsteed e considera la grande somiglianza un caso del tutto fortuito. Lui stesso, però, è molto altalenante e usa valori che vanno da 20” a 9”.

Agli inizi del '700, nuove misure, effettuate su Marte da Maraldi, confermano i risultati di Cassini e Flamsteed e fanno pensare che il valore della distanza della Terra dal Sole possa essere compresa tra i 16000 e i 24000 raggi terrestri, una “forchetta” non proprio incoraggiante. Il metodo legato a Marte, però, sembra non permettere miglioramenti significativi e si arriva alla seconda metà del ‘700 prima di riprendere la questione di petto, affidandosi ad altre tecniche osservative. E qui cominciano anche le grandi avventure…

Nel frattempo, nella Fig. 16 (che è anche la prima del primo articolo), potete vedere i risultati di questa “puntata” segnati con una freccetta rossa.

 

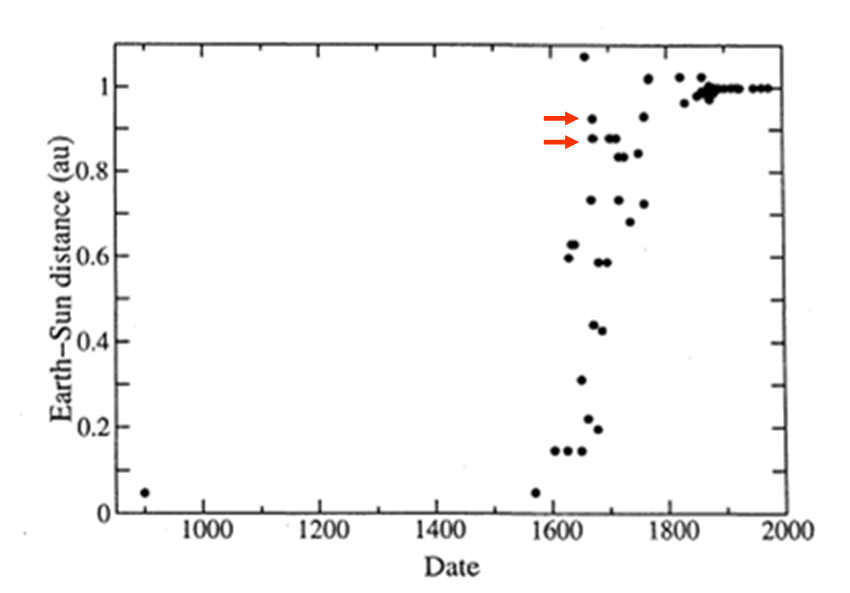
QUI la serie completa degli articoli dedicata alla storia del calcolo della distanza del Sole