Categorie: Meccanica Celeste Sistema Solare Sole Terra
Tags: distanza del Sole leggi di Keplero Marte opposizione perielio quiz
Scritto da: Vincenzo Zappalà
Commenti:4
QUIZ: Marte... aiutaci tu! **
Prima di continuare con la nostra storia della distanza della Terra dal Sole, mettiamoci alla prova con un problemino risolto nel 1672 e quindi di estrema facilità per noi. Tuttavia, vogliamo usare solo ciò che avevano a disposizione a quei tempi. Non andate a cercare nel web dato che troverete sicuramente una parte della risposta, ma, forse, non tutta… Pensateci, quindi, da soli.
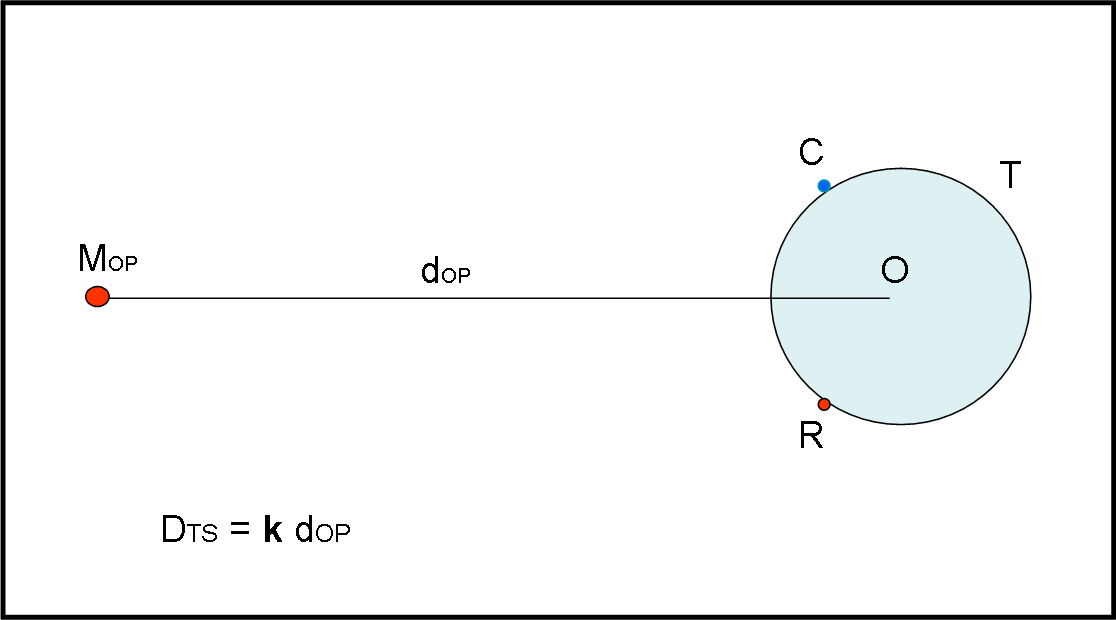
Le condizioni sono ottimali e noi le rendiamo praticamente perfette. La situazione è quella mostrata dalla figura che segue. Marte (M) è all’opposizione e al perielio. C e R sono due astronomi posizionati sulla Terra (T) in due punti diversi della sua superficie . Entrambi conoscono perfettamente la loro posizione in latitudine e longitudine. La distanza Terra-Sole la indichiamo con DTS, quella tra Marte e Terra con dOP.
Quali passi devono essere fatti OSSERVATIVAMENTE e MATEMATICAMENTE per arrivare a una soluzione del tipo:
DTS = k dOP
In particolare, qual è il valore numerico di k ?
Ovviamente, la sequela di operazioni può subire alcune approssimazioni lecite. Chi ne farà di meno sarà sicuramente il ... migliore!
Per rendere il tutto più semplice, possiamo lasciare indicata la distanza dOP (non esageriamo), per cui non indico latitudine e longitudine dei luoghi di osservazione (ma bisogna comunque descrivere esattamente tutti i passaggi usati per ottenerla). Per ricavare k, vi regalo invece questi dati:
Periodo di Rivoluzione della Terra: 365.25 giorni
Periodo di Rivoluzione di Marte: 686.95 giorni
Eccentricità di Marte = 0.09341
La soluzione sarà data nella prossima puntata della lunga storia dell'Unità Astronomica (QUI)






4 commenti
Forza... la gara è aperta a TUTTI. Vinca il migliore (un vero astrofilo dovrebbe andarci a nozze, anche senza celestia...)!
Caro Enzo, visto che nessuno risponde...
Per provare a risolvere il problema, sono partito dalla terza legge di keplero:
a³/P² = G (M + m)/4 π²
Considerato che la massa m di Marte o della Terra sono trascurabili rispetto alla massa M del Sole
è possibile considerare G (M + m(marte))/4 π² ≅ G (M + m(terra)/4 π², pertanto:
a³m/P²m = a³t/P²t
a³m/a³t = P²m /P²t
(am/at)³ = P²m /P²t
am/at = ³√ P²m /P²t
am/at = ³√(686,95)²/(365,25 )² = 1,5236
am = 1,5236 at
Nel caso in esame però Marte si trova al perielio, per cui la sua distanza dal Sole sarà più piccola del suo semiasse am.
Basta una semplice figura per capire come ricavare la proporzione tra semiasse maggiore e distanza del pianeta dal punto di fuoco più vicino (quello occupato dal Sole).
Pertanto: DMS = Distanza di Marte dal Sole al perielio = am (1-e) = am (1- 0,09341)
DMS = 0,90659 am
ma am = 1,5236 at
DMS = (0,90659) (1,5236) at = 1,38128 at
A questo punto si può ricavare il valore di k , ponendo la distanza della Terra dal Sole uguale al suo semiasse maggiore:
DTS = at
Visto che i pianeti si trovano alla minima distanza:
Dop = DMS – DTS = 1,38128 at - at = 0,38128 at
Dop = 0,38128 DTS
k = 0,38128
Per ricavare il valore della distanza media tra Terra e Sole ( DTS), o meglio il valore del suo semiasse maggiore (at) è necessario trovare il valore della distanza Terra-Marte, quando questo è al perielio ed alla minima distanza dalla Terra (Dop).
Per provare a ricavare tale valore è mia intenzione usare l'effetto di parallasse dovuto alla distanza tra i due astronomi.
L'idea è quella di piazzarli entrambi alla stessa longitudine (stesso meridiano), ma a latitudini diverse.
In questa situazione la parallasse dovrebbe determinare una piccola differenza nella misura dell'angolo di declinazione di Marte.
Ogni astronomo per determinare la declinazione di Marte, oltre ad usare alcune vicine stelle di campo di cui è nota la declinazione (le stelle sono molto più lontane per cui la parallasse è piccolissima, trascurabile in questo caso) possono misurare la massima altezza raggiunta dal pianeta rispetto all'orizzonte (culminazione superiore).
Tale altezza massima, misurata in gradi, usando il meridiano locale (linea immaginaria che unisce orizzonte Nord, Zenit e orizzonte Sud del cielo) è pari a:
Altezza massima dall'orizzonte (in gradi) = 90° - Latitudine ° + declinazione°
Nella figura l'altezza massima viene indicata con hmax e il suo angolo come ψ, mentre la latitudine viene indicata con l'angolo φ .
Di fatto, sottraendo la latitudine a 90° (altezza dello Zenit) si ottiene l'altezza massima raggiunta dall'orizzonte dell'equatore celeste, la cui declinazione è 0°.
Aggiungendo la declinazione dell'astro (positiva o negativa), si ottiene l'altezza dell'astro dall'orizzonte.
Pertanto, usando questa semplice proporzione e misurando la massima altezza dall'orizzonte raggiunta da un astro si può ricavare la sua declinazione: hmax = 90°- latitudine + declinazione
Declinazione (σ) = hmax (ψ) + latitudine (φ) - 90°
Un ultima precisazione, l'asse terrestre è inclinato di circa 23,5° rispetto al piano orbitale, per cui il piano dell'orbita di Marte non è parallelo all'equatore terrestre... e la Terra ruota su se stessa...
La figura mostra non solo l'inclinazione della Terra, ma anche cosa dovrebbero vedere due osservatori, che si trovano alla stessa longitudine, ma a latitudini diverse, uno dei quali (A) si trova con Marte proprio sopra la sua testa, allo Zenit.
SEGUE
… ma Marte non si trova ad una distanza infinita, per cui l'angolo di parallasse per quanto piccolo esiste.... nella figura è stata “raddrizzata” la Terra.
A questo punto provo a posizionare i due astronomi, che per semplicità pongo sullo stesso meridiano, ossia alla stessa longitudine, ma uno ad una latitudine di + 45° e l'altro ad una latitudine di -45°.
Nello stesso tempo, il primo astronomo attende che Marte attraversi il mediano locale (la famosa linea immaginaria che unisce Nord, Zenit e Sud), ossia raggiunga il punto dì massima altezza dall'orizzonte (ha), e calcola la declinazione del Pianeta:
Declinazione (A) = ha - 90° + 45° = ha – 45°
Anche il secondo astronomo, attende che Marte attraversi il mediano locale, ossia raggiunga il punto dì massima altezza dall'orizzonte (hb), e calcola la declinazione del Pianeta:
Declinazione (B) = hb - 90° - 45° = hb – 135°
Se non ci fosse la parallasse la Declinazione dovrebbe essere la stessa.
ha – 45° = hb – 135°
135°– 45° = hb – ha
hb – ha = 90°
Un risultato ovvio, dato che l'angolo che separa i due astronomi è di 90° (si passa da una latitudine di -45° ad una di + 45°).
Dunque, per come sono stati posizionati i due astronomi, se la differenza tra le due altezze rilevate ( hb – ha) è minore di 90° (si tratta sicuramente di pochi secondi d'arco), quello è proprio l'effetto della parallasse.
Volendo i due astronomi possono affinare le osservazioni usando come riferimento il valore di declinazione di stelle vicine per apprezzare spostamenti in declinazione molto piccoli... in tal caso:
Declinazione A = Declinazione B (se non ci fosse la parallasse)
per cui se le due declinazioni risultano diverse, la differenza è dovuta alla parallasse:
angolo parallasse α = Declinazione B - Declinazione A
Una volta trovato l'angolo di parallasse è possibile ricavare la distanza di Marte, ma prima bisogna trovare la distanza che separa i due astronomi...
Dato che le loro latitudini sono conosciute, basta moltiplicare il raggio della Terra per il seno dell'angolo di latitudine φ.
Per trovare la distanza Terra-Marte, non resta che applicare la formuletta:
tan (α) = r/d
dove α è l'angolo di parallasse (differenza tra le due misure di Declinazione), r è la distanza tra i due astronomi (misurata in linea retta, ossia la corda che unisce i due osservatori) e d la distanza di Marte dalla Terra (Dop).
d = Dop = r/tan (α)
r = 9009,95 Km
Dop = 9009,95 Km/tan (α)
Quindi, ricordando quanto trovato all'inizio:
Dop = k DTS............ .e..... K = 0,38128
Dop = 0,38128 DTS
DTS = Dop /0,38128
DTS = 9009,95 Km/tan (α) 0,38128
DTS = 23630,80 Km/tan (α)
L'angolo(α), ovviamente, non è altro che la differenza tra i due diversi valori di declinazione trovati, ossia l'angolo di parallasse, ma anche l'angolo con cui un marziano misurerebbe la distanza angolare apparente tra di due astronomi.
Ovviamente è un angolo molto piccolo.... intorno a 30 secondi d'arco nelle migliori opposizioni...
Sembrerebbe funzionare, ma non si sa mai, gli errori sono costantemente in agguato...
Paolo
Paolo, come sempre, è ultra preciso... Diciamo che a fine '600 la coppia di astronomi non poteva scegliere certe posizioni particolari, ma si era dovuta accontentare. Se, qualcuno, preferisce, può anche semplificare di molto la parte "astronomica". Niente da dire, invece, su Keplero (esistono altri modi per ottenere lo stesso risultato, comunque).
Lascio, perciò, aperto il quiz...