29/07/17

Forse siamo alla conclusione del paradosso di Bell **

(QUI e QUI i primi due articoli dedicati al paradosso di Bell)

Ho trovato il lavoro originario di Bell e la chiara affermazione che il nostro ragionamento mentale non ha errori (almeno secondo lui e molti altri… ma io di Bell mi fido molto!)

Ecco una frase più che esauriente di Bell relativa al suo paradosso, estratta direttamente dal suo lavoro originario

…Of course many people who give this wrong answer at first get the right answer on further reflection. Usually they feel obliged to work out how things look to observers B or C. They find that B, for example, sees C drifting further and further behind, so that a given piece of thread can no longer span the distance. It is only after working this out, and perhaps only with a residual feeling of unease, that such people finally accept a conclusion which is perfectly trivial in terms of A's account of things, including the Fitzgerald contraction…

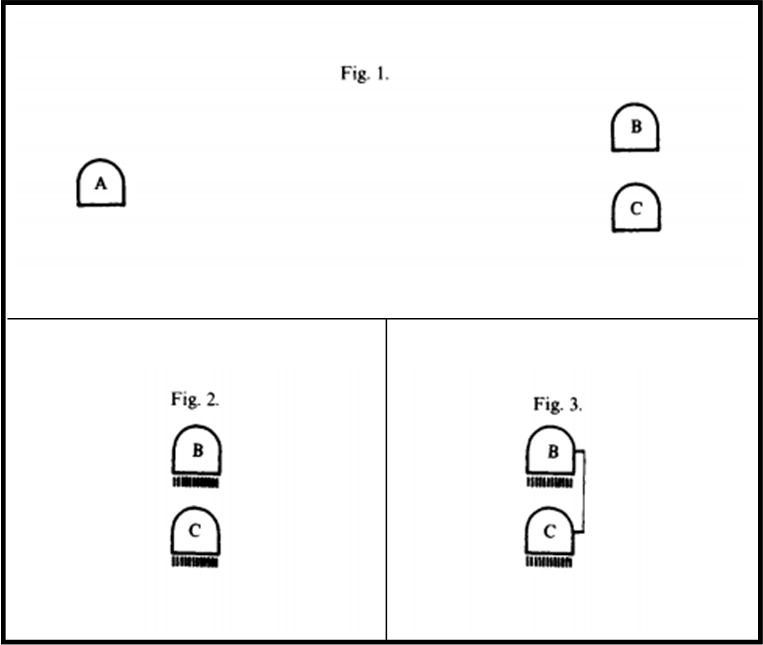
Le prime tre figure, relative al paradosso, estratte dal lavoro di Bell.

Questa la traduzione (le parti in corsivo sono state aggiunte da me per una migliore comprensione)

…Ovviamente, molte persone che hanno dato la risposta sbagliata all’inizio (ossia quella della corda che non si rompe), l’hanno poi cambiata, dopo ulteriori riflessioni. Generalmente, loro si sentivano obbligati a lavorare guardando gli osservatori B e C (i razzi in movimento). Essi hanno dedotto che B, per esempio, vede C allontanarsi sempre di più, in modo che la corda non riesca più a sopportare lo stress dovuto all’aumento della distanza tra i due razzi (la soluzione che dà Petkov e che sembra l’unica sostenibile e l’unica logica). E’ stato solo dopo uno studio più accurato e, forse, con un sentimento di disagio, che queste persone hanno, infine, accettato la conclusione veramente banale ottenibile in termini del solo sistema in quiete A, compresa la contrazione di Fitzgerald (ossia quella che abbiamo proposto noi in modo ultra semplificato e senza accelerazioni).

Insomma, sembra proprio che il filo si rompa per la contrazione e che questa derivi dallo studio approfondito della materia e delle sue risposte agli stimoli esterni. Le dieci domande che avevo scritto nei commenti sembrano proprio avere come risposta un SI generale.

Un insegnamento per tutti noi (come dice lo stesso Bell)… ma permettetemi di essere contento nel non aver trovato nessun errore nel ragionamento mentale.

Il lavoro originario è QUESTO, mentre un articolo che può essere utile a comprendere l’intera faccenda è QUESTO, con buona pace di Petkov e dei suoi errori abbastanza … marchiani (bastava pensare al muone…), che avevo evidenziato nei commenti dell'articolo precedente.

Tra un po’ cercherò di mettere assieme le parti più importanti e fare un riassunto comprensibile di quanto scritto e commentato nei giorni scorsi… Fortunatamente ci sono stati molti commenti, ma questo fatto molto positivo, comporta il rischio di una certa confusione finale.

Gran finale: risolto il paradosso di Bell!!! Forse...

5 commenti

Pippo

29/07/2017 at 23:38

Egregio Zappalà,

se io non le avessi messo il link all'articolo di Vesselin Petkov, cioè questo :

https://arxiv.org/abs/0903.5128

lei neanche avrebbe saputo della sua esistenza. La sua attenzione si è focalizzata sulla ricerca di eventuali errori di questo relativista , per il semplice motivo che a proporlo sono stato io. Almeno, io la penso cosí, visto che in passato abbiamo avuto dei contrasti e lei in qualche modo voleva prendersi una rivincita. Ma sorvolo su questo, lei mi dirà che mi sbaglio.

Il bug che lei crede di aver trovato, nella trattazione di Petkov, è facilmente rintuzzabile : la contrazione delle due astronavi non c'entra nulla , poiché possiamo pensare a delle astronavi puntiformi , una in testa una in coda al cavo; quello che conta è ciò che succede al cavo, il quale oltretutto può essere agganciato in due punti qualsiasi delle due navi. Del resto, se supponiamo ad esempio che le due navi siano lunghe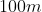 $100m$ , e il cavo sia lungo 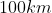$100 km$ , si vede bene che la contrazione relativistica delle navi è trascurabile, rispetto a quella del cavo : è appena un millesimo !

Chiarito questo , mi permetto di presentarle questo fisico :

http://spacetimecentre.org/vpetkov/

che ha fama internazionale, autore di molti libri , e può insegnare la Relatività a molti di noi qui : prima di tutto a me ! E poi anche ad altri . Nel suo articolo , ha analizzato la soluzione di Bell ed ha trovato vari errori . In questa presentazione, fatta a Montreal, ne ha elencati diversi :

http://gpppc6.lps.umontreal.ca/azuelos/Seminaires/08-09/Bell's%20paradox.pdf

il più chiaro di tutti gli errori di Bell ( su cui torno dopo, c'è molto da dire al riguardo) è il seguente :

"According to Bell, the thread will break due to stress caused by length contraction. His conclusion is based on the assumption that physical bodies contract relativistically, but space does not."

Prima però vorrei sottoporre, a lei ed a lettori sinceramente interessati , alcuni link a trattazioni che mi sembrano degne di nota . La prima è la versione inglese su Wikipedia :

https://en.wikipedia.org/wiki/Bell's_spaceship_paradox

poi c'è la dispensa di Jerrold Franklin , che anche lei ha citato :

https://arxiv.org/abs/0906.1919

ci sono considerazioni molto interessanti, anche riguardo al moto accelerato relativistico di un'asta nel senso della lunghezza : per non avere stress nell'asta accelerata, la coda deve accelerare di più della testa ! Strano, vero? Eppure è cosí . Anche questo meriterebbe una trattazione particolare!

Continuando , cito la dispensa piena di calcoli di Sfarti , dove si suppone che il moto relativistico sia iperbolico :

http://fizika.phy.hr/fizika_a/av09/a18p045.pdf

Anche due italiani, Ruggero e Tartaglia, hanno scritto al riguardo :

https://arxiv.org/abs/gr-qc/0301050

facendo vedere la differenza che c'è tra due casi : 1)gli oggetti accelerati sono connessi da un filo, e 2) gli oggetti accelerati non sono connessi da alcun filo.

E potrei continuare, ma ce n'è abbastanza , credo .

Anche lei ha messo il link ad un articolo. Le faccio notare per prima cosa (ma questo lei lo sa molto bene) che quando si disegnano linee di universo curve, come nell'articolo da lei linkato, vuol dire che il moto non è inerziale , è presente una accelerazione. E questo è alla base del paradosso. Nella seconda colonna della prima pagina, l'autore si propone di dimostrare esattamente quello che si sta dicendo, invano, da un sacco di tempo, e cioè :

i lettori sapranno leggere e capire l'articolo, ne sono sicuro.

Ma lei ha proposto una versione semplificata. Lei dice : facciamo muovere a velocità costante le due navi , non vogliamo sapere nulla delle accelerazioni. Poi, l'osservatore ( quello fisso) prende il cavo e lo sistema " a volo" tra le due navi, agganciandolo avanti e dietro . A questo punto, lei dice, interviene la contrazione relativistica , e il cavo si rompe . Ho interpretato bene?

Questo è sbagliato, per me.

Innanzitutto , bisogna capire di che lunghezza è questo cavo , quando è fermo a terra, in attesa che arrivino le navi a folle velocità . È lungo quanto la distanza tra le navi in moto, misurata da terra? E allora è più corto della distanza "di quiete" tra le navi, per il semplice motivo che la distanza tra le navi in moto misurata da terra è la misura "contratta" della distanza di quiete delle navi, cioè della distanza "propria" tra esse. Anche la distanza si contrae , non si contraggono solo gli oggetti materiali , no? 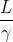Se le due navi, ferme a terra, hanno distanza di quiete $L$ (tra punti uguali, se le aggrada) , quando sono in moto rispetto ad un osservatore , con velocità v uguale per entrambe, la distanza misurata da terra diventa $\frac{L}{\gamma }$ , dico bene ? Lo spazio vuoto subisce la contrazione di Lorentz come gli oggetti materiali , ce lo dicono i muoni , che arrivano a terra dall'alto dell'atmosfera, no?

E perciò , se la corda è lunga, a terra, solo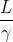 $\frac{L}{\gamma }$ , l'osservatore non potrà piazzarla a volo tra le navi in moto , poiché dovendo acquisire la velocità v istantaneamente la corda avrebbe, rispetto a terra , la lunghezza 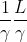$\frac{1}{\gamma }\frac{L}{\gamma }$ , ma la "propria" sarebbe 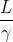$\frac{L}{\gamma }$ , e non può andare a collegare due navi che, nel loro riferimento proprio, distano L . Mi sembra chiaro.

Dunque, la corda non può avere lunghezza propria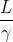 $\frac{L}{\gamma }$ . Deve aver lunghezza propria $L$ , per poterla piazzare tra le due navi che, nel proprio riferimento , distano $L$ .

E se ora osserviamo tutto il sistema da terra, la corda subisce pacificamente la contrazione relativistica , senza rompersi . Infatti, la stessa contrazione relativistica la subiscono sia la distanza tra le navi che la corda : diventano uguali a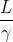 $\frac{L}{\gamma }$ entrambe .

Mi sembra quindi che il solo moto a velocità costante non sia sufficiente a giustificare la rottura della corda.

Del resto, facciamo questo esperimento mentale : a riposo, abbiamo una corda di una certa lunghezza. Davanti e dietro ad essa ci sono due navi, non legate ma semplicemente a contatto con le estremità della corda. Mettiamo in moto, istantaneamente ( è una semplificazione eccessiva...) tutto il sistema, cioè sia le navi che la corda, con la stessa velocità . Corda e navi resteranno a contatto . Questo è il mio parere.

Saluti.
Vincenzo Zappalà

30/07/2017 at 07:19

Innanzitutto, caro Pippo (e io continuo a dare del tu, dato che divergenze interpretative non si devono confondere con astio personale, ma ormai sembra che il mondo non accetti più le discussioni se non sono costellate di insulti e di illazioni varie), se continui in questo tono, completamente opposto allo spirito del circolo, dove tutti hanno diritto a essere ascoltati e trattati con rispetto, sarò costretto a tagliare i tuoi commenti. e sarebbe la prima volta che capita.

Poi direi che per bravo sia Petkov può anche lui commettere errori, come tu asserisci possa aver fatto Bell ( e tra i due... beh... ). L'esempio che fai con i razzi puntiformi semplifica ancora la situazione e rende ancora più chiaro l'errore di Petkov (l'avevo detto di pensare al muone...).

La soluzione è banale: nel caso di due razzi puntiformi (senza contrazione quindi), il sistema in moto vede la distanza tra i due razzi come spazio appartenente al sistema di A e A' (razzo posto nello stesso sistema di A a una distanza a riposo d) e quindi, per lui, questo spazio DEVE contrarsi così come deve contrarsi la corda. Non succede niente. Nel caso semplificato di Bell, lo spazio tra i due razzi puntiformi NON si può contrarre, dato che è spazio del sistema in quiete, mentre la corda appesa diventa in moto e si accorcia. I due esempi sono completamente diversi e chiaramente portano a risultati diversi. Un aiuto in più per capire... La distanza tra A e A' vista da C rimane sempre lo stesso spazio e il tutto si muove di conserva. La distanza tra B e C, vista da A è uno spazio sempre diverso che appartiene ad A e quindi non si muove e non si contrae.

Ovviamente l'ultima tua frase perde di valore, automaticamente.

Tutte le altre disquisizioni riguardo al caso accelerato non interessa al momento, avendo focalizzato il tutto su un unico esperimento mentale.

Ripeto, infine, ancora quanto detto più e più volte. Nel sistema in quiete la corda è lunga come la distanza tra di due razzi (puntiformi). Messi in moto simultaneamente nel sistema di A, la loro distanza con o senza accelerazione non può contrarsi dato che appartiene allo spazio di A e non si muove ASSOLUTAMENTE. La corda è sempre lunga d a riposo, ma una volta agganciata viaggia a velocità v e quindi si contrae e si rompe proprio come si trova lavorando nel sistema in moto... Che si rompa o quello che facciano gli atomi della corda non so... ma di sicuro non può rimanere lunga come la distanza costante tra i due PUNTI razzi.

Avviso che il commento è apparso in ritardo in quanto era stato messo in sospeso a causa del grande numero di link...

Ultimo punto: perché non rispondi alle 10 + 1 domande che ho fatto precedentemente? Lì potresti individuare perfettamente il baco del mio ragionamento e ribaltare i miei convincimenti (e quelli di Bell), con mio sommo piacere, dato che gli esami non finiscono mai e io sono ben lieto di imparare qualcosa di nuovo anche a 72 anni!

Mi raccomando, comunque, il primo punto... su quello non transigo! Ci sono molti altri blog scientifici in cui si dà sfogo alle rabbie personali e a tanti altri sentimenti che con la voglia di conoscere hanno ben poco a che spartire.
Pippo

30/07/2017 at 08:31

Egregio,

proprio non ci intendiamo . Viviamo in uno spazio a curvatura negativa, le nostre geodetiche quindi divergono inesorabilmente...

Per la meditazione sua , e di altri lettori volenterosi, metto un altro link. Viene chiarito ancora una volta il motivo, ormai universalmente accettato, per cui le due navi, viaggiando all'unisono con gli stessi ritmi ( mi sia consentita questa semplificazione di linguaggio) si separano inesorabilmente, a causa della accelerazione ; e quindi, un tenue filo inizialmente disposto tra esse si romperebbe subito , a causa di questa separazione e non per la "contrazione di Lorentz. Nel secondo esempio, tuttavia, si suppone che il sistema delle due navi più la corda che le congiunge costituisca un unico sistema , e allora siamo di fronte a due iperboli , di testa e di coda, che costituiscono una coppia di linee di universo di quelle che si chiamano "coordinate di Rindler" , che lei conosce , ma forse non tutti i lettori .

http://math.ucr.edu/home/baez/physics/Relativity/SR/BellSpaceships/spaceship_puzzle.html

Un'ultimissima considerazione elementare : un cavo si rompe non perché "si contrae" secondo Lorentz, ma perché si tira , al mio paese! e la tensione supera il carico di rottura del cavo .

LA contrazione di Lorentz non induce alcuno stato di sforzo nel corpo contratto; si tratta di fare una diversa sezione del tubo di universo quadridimensionale, descritto dal cavo , fatta con una linea di contemporaneità diversa da quella propria. Lo spiega Minkowski, e lo ribadisce Petkov , che non sbaglia. E cosi succede , per tanti altri apparenti paradossi . Il tubo di universo, nel piano di Minkowski, è la porzione di piano delimitata dalle linee di universo di testa e di coda di un oggetto lungo : se si tracciano rettilinee e parallele , si ha il moto inerziale a v = cost .

In quanto alle sue considerazioni su astio, rabbia , et similia , lascio correre . Non mi appartengono, questi sentimenti. Non si preoccupi, tolgo veramente il disturbo , ora. Spero solo che i link da me postati possano giovare a qualche altro lettore volenteroso, che desidera ascoltare anche qualche altra campana. La mia voglia di conoscere non può fermarsi qui .

Cordialità a tutti .
Vincenzo Zappalà

30/07/2017 at 08:43

Vorrei ritornare al problema originario (quello accelerato gradualmente) e introdurre un tentativo di risposta più realistica.

In questa situazione, diventa banalissima la rottura della corda nel sistema in moto. Le accelerazioni non sono simultanee e quindi la prima astronave si trova sempre più "avanti" costringendo la distanza tra loro ad aumentare e a spezzare una corda che non cambia lunghezza propria.

Andiamo nel sistema fermo, quello che crea i problemi più grossi. Le accelerazioni sono sempre simultanee, il che vuole anche dire che le velocità istantanee si mantengono, che, a sua volta, vuole anche dire che la distanza d tra i razzi è sempre la stessa. Lei se ne cura poco dato che appartiene al sistema in quiete. Anche la corda fa lo stesso e rimane sempre uguale nel sistema in quiete ed è uguale a d. Quando viene inserita simultaneamente, entrambi i suoi capi sono in movimento e quindi la distanza tra di loro deve contrarsi. Il segnale di contrazione parte dai capi e deve raggiungere tutti gli atomi. Inoltre abbiamo un aumento continuo della velocità della corda e quindi una contrazione sempre più forte che viene trasmessa alla struttura corda. Ovviamente l'informazione è rapidissima rispetto alla lunghezza della corda, ma potrebbe essere non trascurabile a livello particelle che decidono il da farsi a velocità comparabili. Il pensare che la corda si contragga tutt'assieme può essere fisicamente irrealistico, ma ancora più irrealistico può essere il fatto che essa non subisca in qualche modo la differenza continua di contrazione. Poveri atomi! Il succo è, però, sempre lo stesso: la corda si rompe per la contrazione, ma questa nasconde un caos terribile nella struttura atomica della corda. Perché, allora, non pensare che sia questo caos di informazioni e di cambiamento di stato delle particelle a causare la contrazione letale?

Ciò non distrugge certo la relatività ristretta di Einstein, che dimostra senza errori cosa succede alla fine e ci permette di schematizzare il tutto accettando cambiamenti drastici e simultanei di velocità. Tuttavia, molto, a questo punto, dipende dal tipo di rigidità che si vuole introdurre e sappiamo che una rigidità assoluta non è compatibile con la RR. E ciò potrebbe dimostrare, in modo più subdolo, che la contrazione sia proprio un fenomeno legato alla velocità dell'informazione.E nemmeno dobbiamo dimenticare che una contrazione fisica comporta comunque accelerazioni e decelerazioni, come ci aveva mostrato il bacherozzo...

Questa visione un po' più articolata e più rispondente al paradosso originario, metterebbe anche d'accordo certe ipotesi fatte da Fabrizio (se non sbaglio) e forse anche da altri... Tutto, però, viene risolto accettando in modo completo che la distanza tra i due razzi, puntiformi oppure no, rimanga sempre la stessa.
Vincenzo Zappalà

30/07/2017 at 09:06

caro Pippo,

ancora una volta tu ti limiti al caso visto dal sistema in movimento, che è ormai cosa consolidata per tutti. Io invece ti chiedo di spiegarmi perché la corda si rompe nel sistema in quiete (DEVE farlo per definizione). Bell ha dato una risposta. Petkov ha fatto un esempio completamente sbagliato per distruggerlo, dato che simula un esperimento completamente diverso (non hai niente da dire su quello?). Il link lo conoscevo bene, ma non lede assolutamente una visione alternativa. Conosco poi dei casi fisici in cui qualcosa si restringe davvero (una maglia di lana...)

Comunque sia, continua pure a non rispondere alle mie dieci domande e a girare attorno al problema che ho sollevato, portando la soluzione del sistema in moto (ormai ben conosciuta, te lo assicuro!). Grazie per i link, facilmente recuperabili su internet, e spero ardentemente che tu possa trovare altrove quelle risposte e/o quelle conferme che qui per noi sono ancora troppo troppo complicate. Resta il fatto che considerare Bell un povero cretinotto incompetente è abbastanza rischioso...