Soluzione del QUIZ: UN UBRIACO E UN PORTONE.

11/02/18

Soluzione del QUIZ: UN UBRIACO E UN PORTONE.

Categorie: Matematica Tags: Scritto da: Umberto Cibien Commenti:4

Il quiz( che trovate Qui) è stato risolto (in un modo o nell'altro) da tutti  i partecipanti. Ricordo  il succo del discorso:

Un ubriaco deve aprire un portone ed ha un mazzo di chiavi;le due domande erano queste:

1° caso: numero medio di tentativi lasciando sempre tutte le chiavi nel mazzo.

2° caso:numero medio di tentativi togliendo la chiave dal mazzo se non apre il portone.

Per risolvere primo caso, basta consultare la teoria dei processi Bernulliani sviluppata in un articolo che trovate qui. Comunque analizziamolo in breve.

Se ad ogni tentativo la chiave viene lasciata nel mazzo , ci troviamo in un processo Bernulliano, ovvero la ripetizione di un esperimento dove le prove sono indipendenti, in quanto ad ogni nuovo tentativo le due probabilità, successo e insuccesso restano costanti;  abbiamo visto che il numero medio di tentativi è dato da:

E(T)=p\cdot \sum_{n=1}^{\infty}n\cdot q^{n-1}=p\cdot \frac{1}{(1-q)^{2}}=\frac{p}{p^{2}}=\frac{1}{p}

p è la probabilità di successo; nel nostro caso p=1/7 oppure in generale p=1/n se n è il numero di chiavi.Quindi E(T)=n . In questo caso sappiamo che abbiamo a che fare una somma infinita del numero di tentativi pesato con la sua probabilità. Infatti   il processo può durare indefinitamente . Se indichiamo con F il fallimento e con S il successo ,possiamo fare uno schema di questo tipo:

1 2 3 4 5 6
S FS FFS FFFS FFFFS FFFFFS

chiaramente questa tabella prosegue all'infinito; nel nostro caso p=1/n, mentre q (insuccesso) q=n-1/n, E(T)=n

Per calcolare per esempio la probabilità che esca la chiave al quarto tentativo, lo schema è  FFFS

quindi  la probabilità sarà q\cdot q\cdot q\cdot p=(\frac{n-1}{n})^{3}\cdot \frac{1}{n}

Perchè rifaccio questi conti che conosciamo già bene? Perchè voglio fare una analogia con il caso 2) dove la chiave che non apre viene tolta dal mazzo.

Qui il processo però è  finito; ogni volta tolgo una chiave quindi alla fine resto con una chiave sola.

Supponiamo che la chiave giusta venga al primo colpo; la probabilità è chiaramente 1/n. E se invece viene al secondo?

Lo schema logico sarà questo: FS; ma anche il fallimento ha una sua probabilità, che sarà   n-1/n; la probabilità che adesso venga un successo non è più 1/n, in quanto una chiave è stata tolta. Sarà dunque 1/n-1.

Adesso devo moltiplicare le due probabilità: \frac{n-1}{n}\cdot \frac{1}{n-1}=\frac{1}{n}; quindi anche per avere la chiave giusta al secondo tentativo la probabilità è 1/n.

Andiamo avanti; schema logico FFS; il primo fallimento avrà probabilità n-1/n,il secondo( n-2)/(n-1) mentre il successo F 1/(n-2) quindi \frac{n-1}{n}\cdot \frac{n-2}{n-1}\cdot \frac{1}{n-2}=\frac{1}{n}, quindi la probabilità di avere successo al terzo tentativo risulta ancora 1/n.

Riassumendo e indicando con k il numero di tentativi, e con S(k) la probabilità:

k=1  : S(1)= 1/n

k=2: S(2)= \frac{n-1}{n}\cdot \frac{1}{n-1}=\frac{1}{n}

k=3:S(3)= \frac{n-1}{n}\cdot \frac{n-2}{n-1}\cdot \frac{1}{n-2}=\frac{1}{n}

come potete vedere, la probabilità è sempre 1/n.

Chiaramente k<=n

Questa però non è una dimostrazione rigorosa; per chi vuole approfondire scriverò tale soluzione alla fine dell'articolo.

La probabilità risulta dunque costante ad ogni numero di tentativi; per fare il valor medio dei tentativi  dobbiamo pesare i tentativi con la loro probabilità:

E(T)=\sum_{k=1}^{n}\frac{1}{n}\cdot k=\frac{1}{n}\sum_{k=1}^{n}k=\frac{1}{n}\frac{n(n+1)}{2}=\frac{n+1}{2}

dove abbiamo usato l'a formula di Gauss per la somma dei primi n numeri interi (1+2+3+....n)=\frac{n(n+1)}{2}

Nel nostro caso, in cui n=7

1° caso: numero medio di tentativi lasciando sempre tutte le chiavi nel mazzo:

E(T)=\frac{1}{p}=\frac{1}{\frac{1}{n}}=n; quindi E(T)=7

2° caso:numero medio di tentativi togliendo la chiave dal mazzo se non apre il portone.

 

(n+1)/2=(7+1)/2=4.

Chiaramente, il secondo caso, come si intravede intuitivamente, è quello che ha il minor numero medio di tentativi.

Dimostrazione  rigorosa del valore della probabilità nel caso 2)

Provando per vari valori di k abbiamo ottenuto:

 

k=1  : S(1)= 1/n

k=2: S(2)= \frac{n-1}{n}\cdot \frac{1}{n-1}=\frac{1}{n}

k=3:S(3)= \frac{n-1}{n}\cdot \frac{n-2}{n-1}\cdot \frac{1}{n-2}=\frac{1}{n}

dove k<=n. Ricordiamo che k è il numero di tentativi per ottenere il successo.

Indichiamo invece con P(k) la probabilità di avere k-1 insuccessi, questo per 2<=k=<n

Analizziamo meglio per k=3:

\frac{n-1}{n}\cdot \frac{n-2}{n-1}\cdot \frac{1}{n-2}=\frac{n-2}{n}\cdot \frac{1}{n-2}=P(3)\cdot \frac{1}{n-2}

quindi P(3)=\frac{n-2}{n}\cdot; quindi in generale posiamo scrivere:

3) P(k)=\frac{n-k+1}{n}; applichiamo adesso il principio di induzione per 2<=k<=n

per k=2 la formula è vera, infatti \frac{n-2+1}{n}=\frac{n-1}{n}

supponiamola vera per k, P(k)=\frac{n-k+1}{n} e dimostriamola per k+1

P(k+1)=P(k)\cdot \frac{n-k+1-1}{n-k+1}=\frac{n-k+1}{n}\cdot \frac{n-k+1-1}{n-k+1}=\frac{n-k}{n}

questo è proprio P(k+1) , infatti usando la formula 3):

P(k+1)=\frac{n-k-1+1}{n}=\frac{n-k}{n}

Torniamo adesso alla 3):

P(k)=\frac{n-k+1}{n}; per avere la probabilità di avere un successo al k-esimo tentativo, dobbiamo moltiplicare questo termine per la probabilità di avere un successo dopo aver tolto k-1 chiavi:

S(k)=\frac{n-k+1}{n}\cdot \frac{1}{n-k+1}=\frac{1}{n}       essendo \frac{1}{n-k+1} la probabilità di avere successo dopo aver tolto k-1 chiavi sbagliate.

 

Articoli correlati

4 commenti

  1. Pievani
    20/02/2018 at 09:41

    Buongiorno Vincenzo, ho letto questo articolo nella speranza di far chiarezza su un problema che ho in testa da molto tempo, ovvero il seguente:

    L'umanità gioca a carte da secoli, e mischia i mazzi prima di ogni partita.

    La mia teoria è che l'ordine delle carte di ogni mazzo in ogni tempo non sia mai risultato uguale.

    Semplificando la frase: non è mai esistito un mazzo di 52 carte mischiato uguale ad un altro.

    Questo significherebbe che quando mischio un mazzo, quella è la prima volta che le carte appaiono in quel modo in tutta la storia dell'umanità :)

    Non sono mai riuscito a verificare statisticamente la cosa però...

  2. Umberto
    20/02/2018 at 10:55

    Il numero di modi diversi per mescolare le carte è  52 fattoriale che equivale a 8,0658 *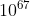 10^{67}

    Non so se tu conosca il fattoriale, ma presumo di si. Altrimenti chiedimi pure. Questo è un numero enorme, perfino se  lo paragoniamo all'età dell'universo , che mi sembra sia circa 10 alla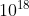 10^{18}. Qualcuno sarebbe tentato di dire che se mescolassimo un mazzo al secondo dall'inizio dell'universo ad adesso, non avremmo trovato nemmeno 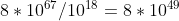8*10^{67}/10^{18}=8* 10^{49} combinazioni diverse che è un numero ancora molto minore a 8,0658 * 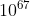10^{67} quindi è impossibile che si ripeta una combinazione.

    Questo può essere un discorso sensato, ma il calcolo delle probabilità ragiona in altro  modo. Potremmo ancora  pensare ad uno schema bernulliano (qui si rimette tutto in gioco ogni volta). Mescoliamo il mazzo per la prima volta: viene fuori una certa combinazione, la probabilità che si ripeta è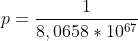 p=\frac{1}{8,0658 * 10^{67}}, mentre che esca un altra combinazione è 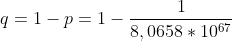q=1-p=1-\frac{1}{8,0658 * 10^{67}} che è un numero molto ( ma molto) vicino ad uno. Per quanto abbiamo visto anche in quest'articolo, non è impossibile che la prima combinazione si  ripeta. Però è molto improbabile.

    Possiamo solo pensare ad un valor medio; ovvero a quante volte dovremmo ripetere la mescolatura. Sappiamo dall'articolo che questo valor medio è proprio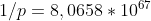 1/p=8,0658 * 10^{67}. Dopodiché ognuno può giungere alle conclusioni che più lo aggradano.

  3. Pievani
    22/02/2018 at 13:26

    Buongiorno Umberto, grazie mille per l'interessamento. In effetti il mio è un pensiero perlopiù filosofico, che si basa su un fatto molto contro intuitivo che vuole ogni mazzo mischiato, diverso da tutti quelli mai mischiati sino a quel momento. Chiaramente esiste la remota possibilità che una combinazione si ripeta, ma è lecito pensare che quel piccolo e banale oggetto che ci troviamo davanti (il mazzo di carte) sia invece unico nel suo genere dall'alba dei tempi. Questo lo rende un pò magico per me :)

     

  4. umberto
    22/02/2018 at 13:29

    in effetti potrebbe essere anche come tu dici, anzi.. Grazie a te per il quesito, non l' avevo mai considerato e conosciuto

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.