Il quiz sembra apparire subito come un paradosso, dato che, "visivamente, una scalinata composta da scalini sempre più piccoli tende a essere confusa con una retta. In realtà, questo passaggio non è un processo matematico, ma un vero e proprio cambiamento di funzione che collega due punti. Tra l'inizio e la fine della scala potremmo far passare infiniti tipi di funzione, ciascuna con la sua lunghezza. Ben diverso è invece cercare di trasformare una funzione in un'altra: scala e retta sono due funzioni diverse e danno risultati diversi senza causare nessun paradosso. 

Abbiamo lasciato, quindi, la descrizione del "finto" paradosso al nostro amico Umberto, mago indiscusso della matematica a tutti i suoi livelli. Un grazie enorme anche a tutti gli altri che hanno cercato (vedi commenti) di trasformare in qualche modo una scala in uno scivolo. Resta il fatto che l'unica creature che potrebbe farlo è la formica... la quale, per dimensioni irrisorie degli scalini, potrebbe decidere di saltare da uno scalino all'altro descrivendo un funzione diversa, non più una scalinata, ma una vera e propria linea (quasi) retta. Questa non è più matematica, però... -al limite- è un approccio "fisico" al problema.

Ho avuto l'incarico di scrivere la soluzione del quiz che trovate QUI. Cercherò di fare del mio meglio, perchè la discussione ha preso le vie più fantasiose, forse a causa delle diverse interpretazioni del testo. Sostanzialmente ho ripreso e ampliato le idee espresse nei mie commenti al quiz.Rispetto tutte le idee espresse, anche perchè per me la fantasia è una componente essenziale della matematica. Comunque la prima cosa che vorrei fare è fissare bene le condizioni, in modo di avere ben inquadrato il problema. Altrimenti ci ritroveremmo a parlare del "sesso degli Angeli", cosa che ben poco centra con la matematica. Riporto l'immagine e la parte cruciale del discorso:

"

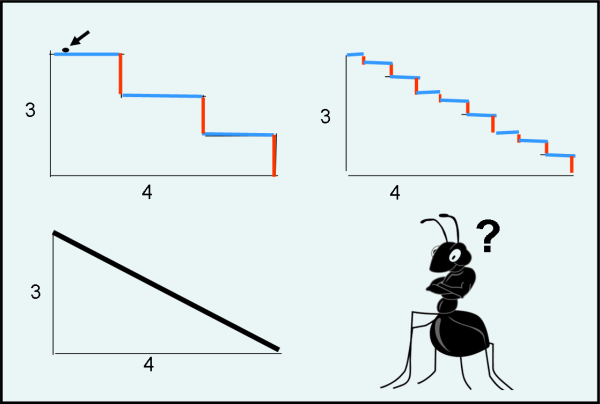
"La formichina è molto stanca e allora chiede a un caro amico topolino, celebre roditore, di ridurre le dimensioni dei gradini (immagine a destra in alto)… chissà che non vada meglio?!"

Questo è un punto cruciale. Per ridurre la gradinata ci vuole un metodo. Se consideriamo il primo gradino della figura in alto a sinistra, ci sono tanti modi per dividerlo. Fatto per me essenziale, è che le divisioni partano da gradini con componenti ortogonali, e creino gradini con componenti ortogonali. Io interpreto così il testo. Niente pedane o scivoli o archi.In secondo luogo la formichina percorre sempre  la gradinata camminando in verticale-orizzontale attaccandosi al gradino; non esegue salti tagliando in diagonale nemmeno quando lo potrebbe fare.  Dobbiamo considerare puntiforme la formica. Potremmo invece lasciare la totale libertà sulle proporzioni di taglio dei gradini.

Matematicamente questo potrebbe tradursi così:

Ho una scala alta 3 m e larga 4 m.

Inizialmente la scala ha un numero finito di scalini, per esempio 3.

Voglio eseguire delle riduzioni dei gradini sezionandoli in verticale e orizzontale, togliendo materiale, in modo di ottenere sempre una gradinata continua con gradini sempre ortogonali e di numero arbitrario, che però uniscano sempre i due estremi della scala iniziale. Non possiamo creare scalinate che vanno su e giù( In tal caso non è nemmeno detto che procedendo all'infinito si abbia una lunghezza finita); lo scalino successivo deve avere la "pedata" più bassa del gradino precedente. Continuiamo queste divisioni all'infinito. Chiaramente l'idea intuitiva che tutti hanno è di modificare gli scalini restando il più vicino possibile alla al segmento AB, che ,chiaramente è la distanza più corta per andare da A a B.

Ci chiediamo quindi due cose:

1. Qual è la distanza percorsa dalla formica, ovvero la lunghezza della gradinata?
2. Che "curva" è la gradinata infinitamente divisa?  E' una retta?

 

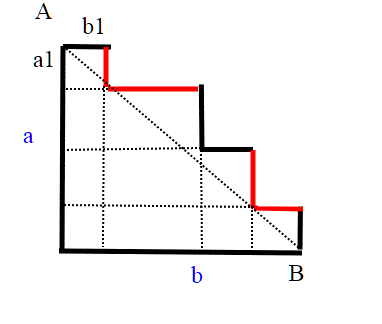
Per me il discorso più semplice, che potrebbe essere stato compreso fin dai tempi dei Greci (che non conoscevano il calcolo infinitesimale), è questo:

La lunghezza della scalinata del disegno è a+b

consideriamo una scalinata qualsiasi e siano a_i, b_i la base e l'altezza dello scalino. I  vincoli imposti sono quelli di cui abbiamo parlato. Se proiettiamo le parti verticali e quelle orizzontali degli scalini rispettivamente su a e b, non facciamo altro che suddividere a e b, ma se poi sommiamo queste suddivisioni otteniamo ancora a e b. Questo qualsiasi sia la gradinata, finita o infinita; avremo quantità costanti, non dipendono dalle suddivisioni.  Quindi la lunghezza è sempre a+b. Non so chi potrebbe dimostrare che non è valido questo ragionamento.  La curva ottenuta dopo infinite suddivisioni non può essere un retta, perchè altrimenti la sua lunghezza sarebbe  ; ma così non è. Quindi la curva non è una retta,ma una scala con infiniti gradini.

Due parole sulla lunghezza di una curva e sugli integrali definiti

L'analisi ci viene incontro quando vogliamo calcolare la lunghezza di una curva derivabile;tutti conoscono la formula

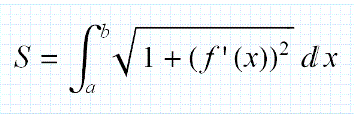
Quello che tutti forse non sanno, è che la definizione di  lunghezza di una curva  viene prima di quella  formula.

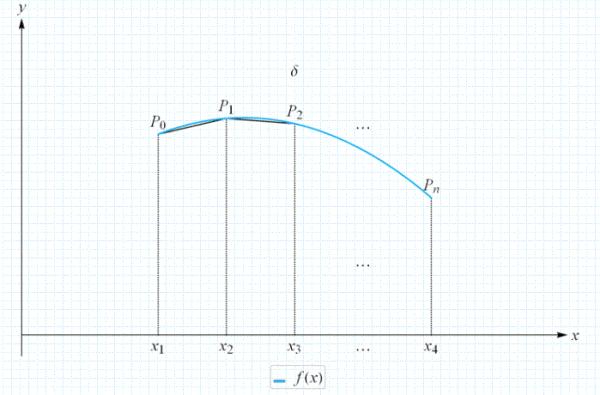
La definizione di lunghezza di un arco di curva è la seguente:

Suddividiamo l'intervallo sull' asse x che sottende alla curva in tanti intervalli   . Costruiamo la poligonale come nel disegno. Per ogni xi troviamo la coordinata y_i=f(x_i) corrispondente. Facciamo poi la somma delle lunghezze P0P1, P1P2,...ecc. aumentiamo sempre di più gli intervalli alla base; ebbene, la lunghezza della curva è per definizione l'estremo superiore della somma di tali lunghezze. In questo caso applichiamo il teorema di Pitagora per calcolare tali lunghezze in funzione delle coordinate, e se la funzione è continua e derivabile possiamo dimostrare la formula sopra. La distanza P0P1 è chiaramente un segmento di retta, la distanza è euclidea. In ogni caso nessuno dice mai che la poligonale tende alla curva, ma solo la sua lunghezza tende a quella della curva.

Il nostro caso è diverso: noi non abbiamo  la curva e dobbiamo trovarne la lunghezza, ma la curva è già scomposta in tratti che sono  i nostri gradini. Se inventiamo un metodo per costruire la curva, possiamo poi esplicitare dei calcoli. In un certo senso siamo avvantaggiati. Se conosciamo il numero e la larghezza dei trattini possiamo semplicemente trovare la somma, di cui poi fare un limite. Volevo ribadire che anche la distanza sui gradini è sempre quella Euclidea; non è altro che l'altezza e la larghezza di segmenti che formano il gradino.

 

Nel caso dell'integrale la questione è ancora diversa; abbiamo una curva assegnata e costruiamo sotto (o sopra)il rettangoloide. Un punto dei trattini appartiene sempre alla curva; in ogni caso qui stiamo cercando l'area sottesa.Tale area è il limite dell'area del rettangoloide quando costruiamo infiniti rettangolini. In ogni caso, per me, non è il rettangoloide  che tende  alla curva, ma è la sua area che tende all'area del trapezoide. Per dirla ancora meglio l'area del trapezoide è l'estremo superiore delle somme delle aree dei rettangoloidi inscritti.

Un metodo ricorsivo per costruire la  gradinata

Se vogliamo complicarci la vita, e fare dei calcoli con le serie, potremmo pensare di generare tale curva con un metodo ricorsivo.

Prendiamo questa procedura ricorsiva per la costruzione della scalinata:

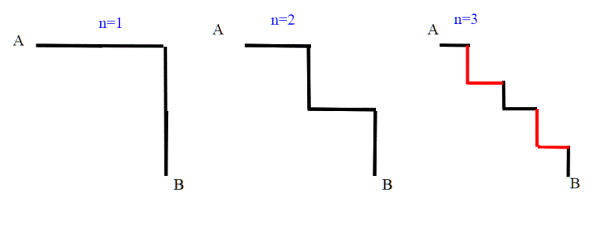
Dividiamo per due il primo gradino, poi continuiamo a dividere ricorsivamente ogni gradino allo stesso modo.Andiamo avanti così indefinitamente. Notare che ci teniamo sempre vicini al segmento AB, quindi sarebbe un buon metodo per cercare di avere il percorso più corto.

Lunghezza della curva

Calcoliamo la lunghezza della curva,intesa come limite di curve ricorsive, facendo il limite per  n-->infinito della lunghezza in funzione di n. Non c'è dubbio che tale lunghezza in funzione di n è costituita dalla somma dei tratti orizzontali più i tratti verticali, per ogni passo della ricorsione.

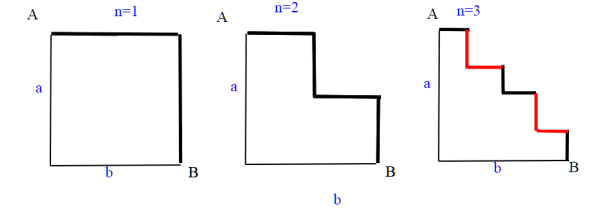
n=1;L(1)=a+b

n=2; L(2)=a/2+a/2+b/2+b/2=a+b

n=3 L(3)=a/4+a/4 + a/4+a/4 +b/4+b/4+b/4+b/4= 4*a/4+4*b/4=a+b

per n generico:

i tratti totali  sono ;    orizzontali,   verticali

quindi un tratto orizzontale è lungo 

mentre un tratto verticale 

L(n)=L0rr(n)+ Lvert(n)

Lorr(n)=

Lvert(n)=

L(n)=L0rr(n)+ Lvert(n)=a+b quindi non dipende da n

Calcoliamo la lunghezza della curva,intesa come limite della lunghezza delle curve ricorsive, facendo il limite per

n-->infinito:

 in quanto il limite di una costante è la costante stessa.

La curva ricorsiva non è una retta

Dobbiamo adesso  astrarci completamente dalla nostra idea di curva o funzione. Il risultato a cui perverremo potrà sembrare assurdo, ma teniamo conto del fatto che la nostra curva non è definita in un modo tradizionale.

Pensando ad un numero sempre più grande di ricorsioni, ci immaginiamo visivamente  che prima o poi vedremo una retta. Ma questa è solo una nostra intuizione. In realtà se poi prendiamo un punto e lo ingrandiamo, avremo delle sorprese. Pensate a delle coste viste da un areo; possono sembrare con dei contorni continui, ma più ci avviciniamo più diventano frastagliate, e addirittura assomigliano all'intera costa stessa. Un altro esempio: disegnate un segmento con un software di immagini; ingrandite il segmento e prima o poi troverete una gradinata  formata dai pixel. Aumentate la risoluzione dell' immagine e ridisegnate la retta; dovrete fare degli ingrandimenti più grandi ma ritroverete sempre la gradinata di pixel. Per noi la risoluzione sarà legata al numero di ricorsioni, mentre gli ingrandimenti saranno dei cambiamenti di scala.

In matematica ingrandire significa eseguire dei cambiamenti di scala.

Prendiamo adesso un punto x0 e il corrispondente punto P su una retta. Se consideriamo fattori di scala sempre più grandi intorno al punto  x0 troviamo sempre dei segmenti (contenuti nella retta).  La curva , invece, vista su qualsiasi scala è  identica a se stessa, a causa della ricorsione.  In parole povere:se facciamo un ingrandimento in un intorno di un punto su una retta, otteniamo sempre un segmento di retta. Ma se lo facciamo sulla nostra curva che apparentemente sembra una retta, ritroviamo sempre qualcosa di simile alla gradinata.

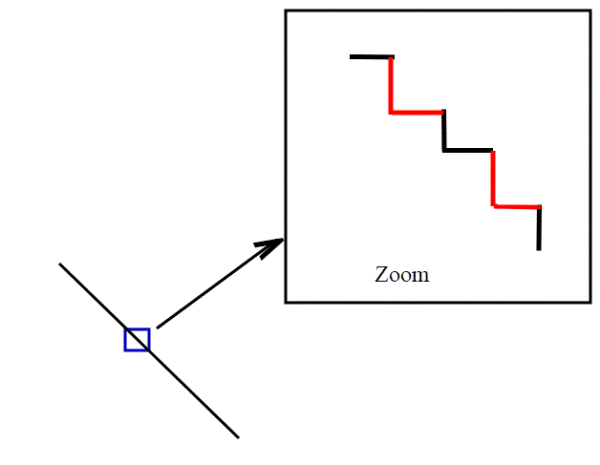
Quindi nessun paradosso; anche se apparentemente sembra tendere ad una retta vista su una certa scala, in realtà resta sempre una gradinata, e quindi  ritorniamo al fatto che la sua  la sua lunghezza è data da a+b; non possiamo usare il teorema di Pitagora applicato ai cateti a e b.  Notiamo inoltre che per nessun valore di n i gradini degenerano a un punto; la loro grandezza orizzontale è   ,quella  verticale ; questi sono numeri >0, è solo il loro estremo inferiore  che è zero.Aggiungo questo; un gradino non può diventare improvvisamente un segmento diagonale nemmeno con un passaggio al limite.

Conclusioni.

Qualcuno potrebbe avere dei dubbi giustificati su tutto ciò, derivanti dalle nostre conoscenze  del calcolo differenziale e integrale. Si potrebbe fare una similitudine fra il calcolo della lunghezza di una curva fatta di tanti trattini infinitesimi o pensare al rettangoloide che sottende una funzione di cui vogliamo fare l'integrale, o a delle funzioni tipo gradino infinitesimo che approssimano una retta. A parte il fatto che per calcolare la lunghezza di una curva si usano le corde che uniscono due punti della stessa,e approssimano la lunghezza del singolo arco, per me il discorso non centra niente. In questo caso abbiamo una curva data (che può essere anche una retta), e ci costruiamo sopra una poligonale di cui fare il limite. Nell'altro non sappiamo , non conosciamo  quale sarà la curva ma possiamo dedurre che non sarà una retta solo dai ragionamenti successivi.

La scala del diavolo

Cito per ultima la funzione di  Cantor-Vitali, definita sull'intervallo [0,1]--->[0,1] , in questo caso sempre crescente; è una curva fatta di infiniti gradini, che in alcuni intervalli diventano molto piccoli, diventando visivamente dei segmenti di retta; ebbene, anche tale curva detta  scala del diavolo ha lunghezza 1 +1=2, ovvero pari alla somma dei cateti che la delimitano.

 

QUI approfondiamo la conoscenza della Scala del Diavolo