Categorie: Matematica
Tags: formica. scala limiti paradosso Pitagora quiz
Scritto da: Vincenzo Zappalà
Commenti:74
QUIZ: il “paradosso” della scala e della formica *
Mentre i nostri maghi si divertono con discese libere su percorsi molto strani, noi ci accontentiamo di un piccolo quiz alla portata di tutti (prego i più esperti di pensare ad Achille e di non invadere questo quiz semplice semplice). E’ veramente una banalità, ma vorrei premiare la migliore soluzione…
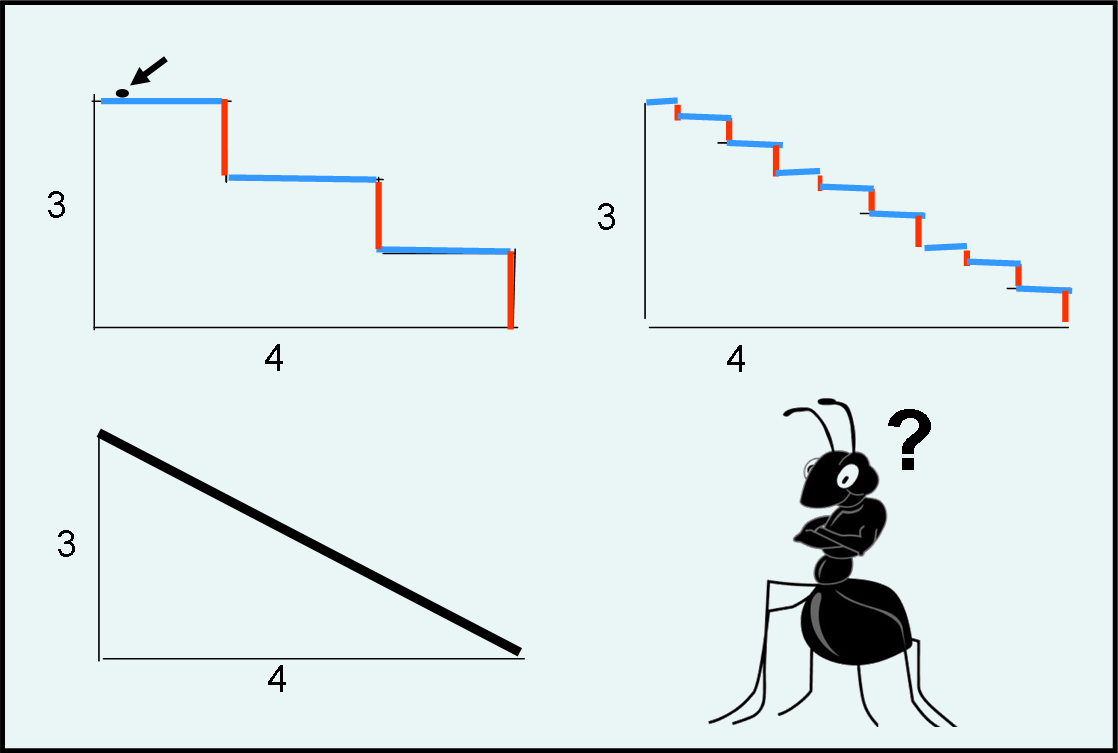
Quello che proponiamo è una specie di “paradosso”. Una simpatica formichina deve scendere e salire continuamente una scala, alta 3 e lunga 4 metri. La vediamo nell’immagine in alto a sinistra. Quanti metri deve percorrere per scenderla? Beh… molto facile: deve percorrere in orizzontale tutti i tratti blu e in verticale tutti i tratti rossi. Quanto vale la somma dei tratti blu? Sicuramente 4 metri. Quanto vale quella dei tratti rossi? Altrettanto sicuramente 3 metri.
In totale, la formichina deve percorrere 4 + 3 = 7 metri sia in discesa che in salita.
La formichina è molto stanca e allora chiede a un caro amico topolino, celebre roditore, di ridurre le dimensioni dei gradini (immagine a destra in alto)… chissà che non vada meglio?!
Purtroppo, la faccenda rimane sempre uguale… La formichina percorre sempre 4 metri in orizzontale e 3 metri in verticale. Ossia 7 metri.
La formichina si ferma a pensare e poi trova l’idea vincente: chiede al topolino di fare degli scalini piccolissimi. Così piccoli e tanti che non si vedono nemmeno ad occhio anche se ci sono. In pratica la scala diventa quella dell’immagine a sinistra in basso. Non c’è bisogno di fare troppi calcoli sui gradini, praticamente infinitesimi come dimensioni e infiniti come numero. L’errore che potrebbe commettere sarebbe piccolissimo. Basta utilizzare il teorema di Pitagora ! Il percorso sarà praticamente uguale a √(32 + 42) = √25 = 5 metri!
Fantastico! La formichina deve percorrere soltanto 5 metri invece dei soliti 7.
In fondo, non ha fatto altro che passare al limite per un numero di gradini che tende a infinito e che sono sempre più piccoli. Eppure, la faccenda sembra veramente paradossale.
Ci deve essere qualcosa che non va… Un premio “cosmico” a chi lo sa spiegare meglio.
Un premio aggiuntivo a chi dimostra che in fondo, in fondo, la faccenda potrebbe, sotto certe condizioni, funzionare realmente!
Fate pensare anche i bambini…
QUI la soluzione






74 commenti
Non possiamo modificare le dimensioni degli scalini, senza contemporaneamente cambiare la "taglia" della formica. Infatti se la formica fosse lunga 100 m. non si renderebbe nemmeno conto dell'esistenza della scaletta e la distanza da superare sarebbe di soli 4 m. !
La formica resta formica e le sue dimensioni sono normalmente molto più piccole degli scalini... Comunque, il paradosso del salto da 7 metri a 5 resta... oppure no?
Si, la formica è piccolina, ma è pur sempre 1/40 dello scalino. Se dividiamo lo scalino per
400, la formica diventa 10 volte più lunga! E continuando progressivamente, la formica non dovrà più percorrere la discesa verticale fra un gradino e l'altro, ma procederà in diagonale!
Marlelio.
cari ragazzi,
voi avete essenzialmente ragione. Ma avete risposto alla seconda parte della domanda, ossia a la faccenda potrebbe, sotto certe condizioni, funzionare realmente! Ossia saltare i gradini, in pratica passare da uno spigolo all'altro.
La prima parte voleva una spiegazione del come mai pur aumentando il numero degli scalini verso infinito, così come riducendo l'altezza verso zero, il valore rimane sempre 7, mentre, poi, il limite diventa esattamente 5? Che tipo di funzione è mai questa ????
Accettiamo anche le risposte dei più bravi e vediamo chi sa spiegare meglio cosa avviene...
Mi sembra che i criteri di valutazione del percorso siano due : uno si basa sulla distanza pitagorica, l'altro (il primo nella narrazione) si basa sulla distanza di Manhattan(o del taxista). Se si passa da un criterio all'altro le cose cambiano, per Pitagora la distanza vale 5 per il taxista vale 7. Ognuno, a suo modo, ha ragione.
Una esposizione precisa di questi concetti si trova nella soluzione del quiz "Quazel contro Euclide" a questo link
http://www.infinitoteatrodelcosmo.it/2018/01/15/soluzione-al-quiz-quazel-euclide/
caro Oreste,
questa conclusione mi piace abbastanza, ma forse basterebbe rimanere nel caso della somma. Per piccoli che siano gli scalini e per grande che sia il loro numero, la somma delle altezze e delle lunghezze rimane sempre e soltanto 7. Il limite della lunghezza (o altezza) dello scalino per n che tende a infinito, tende a zero, ma la lunghezza totale è una forma ∞ • 0 che è indeterminata, ma vale sempre la lunghezza del lato.
La diagonale, invece è tutta un'altra funzione (continua). Gli scalini non tendono mai come limite alla diagonale...
Che ne dite?
Anche io aspettavo una valutazione migliore della mia....

insomma, mi piacerebbe sapere come la vedono i vari maghi & co... (ma anche tutti gli altri, ovviamente).
Qualsiasi sia il fattore di riduzione, i gradini, hanno sempre tutti la stessa forma : alzata e battuta sono i cateti di un triangolo rettangolo e , con l'ipotenusa, formano una terna pitagorica 3 4 5).
Ciascun minuscolo gradino è l'immagine ridotta di questo triangolo, la somma dei cateti resta maggiore della ipotenusa, anche se visivamente la scala appare come una linea costituita dagli infiniti triangolini simili.
In definitiva stiamo parlando di funzioni diverse che, da un punto di vista macroscopico, "sembrano" essere uguali.
io mi associo a Oreste, e non certo perché quell articolo lo abbia scritto io. Per me è fondamentale come si misurano le distanze. Per misurare una curva con il calcolo differenziale si usa il.limite della poligonale inscritta ma le distanze che compaiono nella somma di cui si fa il limite è sempre quella pitagorica. A cosa tenda quella funzione ricorsiva non so, mi viene in mente la scala del Diavolo di Vitali.. Comunque l affermazione che tendeva al segmento inclinato era data come vera nel testo del quiz
diciamo che l'impressione è quella, ma non la realtà...
comunque hanno lo stesso integrale... propenderei anch'io con il post di Mau, ma...
Forse la vera differenza è come nella funzione a gradini, in cui il lato verticale è del tutto inutile. In realtà è quello che capita nell'integrale... conta solo il dx e una sola y per ogni trattino. In tal modo, il limite è proprio la diagonale e non la lunghezza orizzontale. Insomma, qualcosa del genere... che ne pensate?
Aggiungo... la funzione è continua a tratti, ossia a scalini. Tra un tratto e l'altro vi è discontinuità... Ciò che bisogna confrontare è la diagonale con una serie di trattini orizzontali discendenti... Così la distanza finale è proprio quella giusta. Il cateto sarebbe, invece, composto dagli stessi trattini senza salti di discontinuità...
In parole povere, se adeguiamo la dimensione della formica a quella dello scalino, noi potremo aumentare all'infinito il numero degli scalini, ma la scala non sarà mai una retta, ma una linea seghettata, e non potremo quindi applicare il teorema di Pitagora.
Marlelio
io penso che se si fa la divisione anche infinita e si fa la somma delle dx e delle dy tale somma deve sempre dare il lato x e il lato y; si potrebbe anche pensare di dividere per due progressivamente i due lati .. verrebbero due serie convergenti, chiaramente ai rispettivi lati.
direi che sono funzioni diverse...
Consideriamo un cerchio e i poligoni regolari che si possono inscrivere in esso.
Iniziamo con il triangolo equilatero. il suo perimetro è ben diverso dalla circonferenza.
Passiamo al quadrato, poi al pentagono, esagono , ettagono, ottagono e via dicendo.
Ogni volta che aumentiamo il numero di lati del poligono, il singolo lato diventa più piccolo ma, progressivamente, il perimetro aumenta avvicinandosi alla misura della circonferenza, che verrà al limite raggiunta con infiniti lati.
Il particolare fondamentale è la progressività dell'avvicinamento al limite. il percorso curvilineo viene approssimato dalla corda, ma ogni volta che aumentiamo il numero di lati, l'arco si appiattisce di più sulla corda finché , con un numero di lati infinito, le due forme coincidono.
Nel caso della scala, passando da pochi gradini grandi a molti gradini piccoli, non cambia nulla non si verifica alcun progressivo avvicinamento alla misura euclidea di 5 . Le due forme restano identiche, anche alla fine con un numero di gradini infinito e altrettanto distinte restano le due misure.
La improvvisa discontinuità (apparente) che fa dire che la lunghezza non è più 7 ma 5 nasce solo dal passaggio (non autorizzabile) da un sistema di misura delle distanze all'altro.
mi trovi d'accordo... ma nelle funzioni a gradini che servono agli integrali come la mettiamo?
Forse fraintendo la domanda ma quello che penso sia importante nella sostituzione della forma della striscioline degli integrali di una funzione con "trapezi" equivalenti, è l'area.
Immagino una strisciolina come un trapezio rettangolo con il lato obliquo rivolto verso l'alto. Non mi interessa il perimetro di questa strisciolina ma la sua area, che dipende solo dalla base e dalla altezza media.
Negli integrali si cerca un area non una lunghezza. Comunque ribadisco che per me dividendo e poi sommando non si può che ritrovare i due lati
Beh... per avere l'altezza bisogna sapere l'andamento del punto. L'insieme dei trattini deve alla fine coincidere con l'andamento della curva...
Voglio dire che stringendo sempre più i dx ottengo proprio la curva e quindi la lunghezza della curva è uguale alla lunghezza dei trattini per dx che tende a zero. O no?
Guardate che sono d'accordo anch'io, ma vorrei trovare un modo chiaro e semplice per accettare la discordanza apparente...
Ad esempio... se faccio tendere a zero i dx ottengo il lato verticale. Se faccio tendere a zero i dy ottengo quello orizzontale. Se li faccio tendere assieme ottengo la diagonale???
Faccio un altro discorso: la distanza percorsa non dipende dalle divisioni., è sempre 7. Se le divisioni sono n , la distanza è costante, non dipende da n. Se n tende a infinito resta sempre n perché il limite di una costante è la costante stessa
Comunque per me non tende alla retta, i dx e dy vanno assieme non sono indipendenti. Per me è una funzione infinitamente frastagliata.
va beh... accettiamola così. In pratica sono due funzioni del tutto indipendenti. Se non c'è di meglio... mi adeguo, anche perché era la mia idea originale... ma non mi convince ancora del tutto...
Mettiamola così, per adesso:
dal punto di vista fisico, hanno ragione Marlelio ed Elio: la formica rimane quella che è e il passaggio da movimento orizzontale a verticale, si trasforma automaticamente in moto diagonale, quando le gambette possono tranquillamente passare da un gradino orizzontale a un altro.
Il problema nasce quando la formica decresce come lo scalino. Potremmo concludere che non si è mai vista una formica di Planck?
Dal punto di vista geometrico, forse non dovremmo contare il lato verticale, in quanto è un punto di discontinuità. In ogni modo potremmo fare delle medie su piccoli intervalli orizzontali e il valore medio starebbe sulla diagonale. Ad ogni gradino potremmo sostituire il suo punto medio e se il gradino diventa sempre più piccolo la faccenda si trasforma in una serie infinita di punti piazzati lungo la diagonale.
La diagonale potrebbe anche essere considerata come la linea media che approssima la funzione a gradini, ma in questo caso resterebbe sempre un punto di passaggio da somma dei lati a somma delle diagonali.
Forse, alla fin fine, il vero motivo è proprio il modo di misurare....
Si, non c'è alcun paradosso.Maurizio, la funzione "gradinata" non è però una retta. Il problema è proprio questo; sono due linee diverse. Faccio notare una cosa; quando calcoliamo la lunghezza della curva sommiamo i lati delle poligonale inscritta , ovvero delle corde che approssimano l'arco. Qui avrebbe già più senso, perchè effettivamente al tendere delle suddivisioni all'infinito la corda tende all'arco. Ma in ogni caso non è la poligonale che diventa una curva, bensì la sua lunghezza tende a quella della curva. La curva è l'estremo superiore delle poligonali inscritte, ma le poligonali restano poligonali.Ma se facciamo un" ingrandimento" (e in matematica possiamo sempre farlo) troviamo sempre una spezzata, come se ingrandiamo la nostra funzione otteniamo sempre una gradinata, proprio perchè è cosi definita.In ogni caso la lunghezza della gradinata, essendo somma di somme di cateti che sono diverse della diagonale dei piccoli cateti, è diversa dalla lunghezza della diagonale, anche passando al limite.
In realtà la misura è sempre quella euclidea; sono sempre segmenti orizzontali,verticali o diagonali. Sono le linee che vogliamo misurare che sono diverse: gradinata e retta. se poi mi si dice che la formica "salta" in diagonale invece che percorrere la gradinata, allora non percorre la gradinata ma le diagonali.
Per dimostrare formalmente tutto ciò ci vorrebbe stabilire un algoritmo per aumentare i gradini ad ogni passo.
Questo da punto di vista geometrico naturalmente, dove un punto è un punto e un segmento. se poi si passa alla struttura della materia,proprio non saprei cosa dire.
se non ci mettiamo d'accordo su come si può costruire la funzione gradinata, il problema resta un po' come quello di achille e la tartaruga; finchè non venne correttamente matematizzato con il calcolo differenziale, restò opinabile.
Se siamo d'accordo su questo metodo per generare la scalinata , potrei cercare di dimostrare due cose
1)la lunghezza della gradinata è pari alla somma dei cateti
2) la gradinata infinita non è un segmento di retta.
Un metodo ricorsivo per generare la scalinata potrebbe essere questo:
da ogni gradino generato ne ricavo altri due, e procedo all'infinito in modo ricorsivo.
siamo nelle tue mani Umberto!
ok ci provo
Bene! Ma non perdetevi il quiz dell'esploratore ( a te piacerà senz'altro... e anche a Mau e Andy)....
Aiuto!
Non un solo momento di tregua...
vi voglio attivi e mai silenti....
La scala "isomorfa" proposta è autosimile ad ogni scala ma non è analizzabikle con metodi alla Mandelbrot. la sua dimensione non è frattale e rimane sempre costante ad ogni scala, quialunque sia la dimensione infinitesima considerata. Per inciso la scala non è né continua né derivabile, mentre la scala Cantor-Vitali detta del "diavolo" è continua in ogni punto e ha sempre derivata zero escluso i punti dell'insieme di Cantor. Qui siamo in presenza di una funzione la cui derivata oscilla tra zero e infinito in tutti gli intervalli.
Detto ciò per poter dare un senso al valore della distanza calcolata con il teorema di Pitagora, possiamo fare un passaggio al limite in questo modo:
Consideriamo ogni gradino infinitesimo costituito da una funzione gradino o di Heaviside centrata in frazione di 3/4
con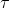 che corre da 0 a 4.
che corre da 0 a 4.
La nostra scalinata sarà quindi la somma di infinite funzioni H(x) centrate in multipli
di 3/4.
sostituendo convenientemente le variabili :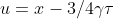 e
e 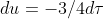
ovvero
ma) è la funzione Rampa(x) cioè una retta di pendenza unitaria.
è la funzione Rampa(x) cioè una retta di pendenza unitaria.
La lunghezza di una funzione f si calcola con l'integrale
Nel nostro caso la funzione è semplicemente f(x) = 3/4 x la cui derivata è la costante 3/4.
E così tutto torna.
Ciao Leandro. Quello che capisco è quanto segue...
La lunghezza 5 è la lunghezza della funzione rampa. (Intervallo 0 4).
La funzione rampa è l'integrale della funzione gradino.
Il valore 5 è la misura lungo questa funzione lineare che rappresenta la crescita dell'area sottesa dai gradini.
Il valore della lunghezza della scalinata. che è costituita dalla somma della funzioni gradino resta una cosa diversa e vale 7.
Questo concilia i due valori ? Oppure l'interpretazione da dare è diversa?
Come ha detto il Professore, portando la costruzione al limite la scalinata dovrebbe divenire un segnement lineare che congiunge gli estremi della scala. Applicando Pitagora tale segmento è lungo 5, a fronte dei lati 3 e 4 . Solo effettuando uan operazione di limite si può ottenere questo valore che corrisponde ad una metrica euclidea, altrimenti la scala è lunga 7, secondo la metrica "del tassista".
E' il passaggio al limite che pone qualche incertezza. Quale funzione usare veramente? Potresti, Leandro, spiegare un po' più terra-terra la funzione che proponi? So che anche Umberto ci sta lavorando... Io sono d'accordo nel separare ogni singolo scalino orizzontale in una funzione singola e farla crescere di numero e diminuire di lunghezza. Alla fine dovremmo avere solo una serie di punti... che segue la diagonale... Se vuoi inserire una figura basta chiedere a Scherzy...
Vi espongo le mie idee su una possibile soluzione del paradosso, in modo semplice, affinché possano capire tutti.
Come costruire la scala infinita del quiz? Un modo naturale è usare la ricorsione (potrebbe farlo anche il roditore).
Prendiamo questa procedura ricorsiva per la costruzione della scalinata:
Dividiamo per due il primo gradino, poi continuiamo a dividere ricorsivamente ogni gradino allo stesso modo.Andiamo avanti così indefinitamente.
Lunghezza della curva
Calcoliamo la lunghezza della curva,intesa come limite di curve ricorsive, facendo il limite per n-->infinito della lunghezza in funzione di n. Non c'è dubbio che tale lunghezza in funzione di n è costituita dalla somma dei tratti orizzontali più i tratti verticali, per ogni passo della ricorsione.
n=1;L(1)=a+b
n=2; L(2)=a/2+a/2+b/2+b/2=a+b
n=3 L(3)=a/4+a/4 + a/4+a/4 +b/4+b/4+b/4+b/4= 4*a/4+4*b/4=a+b
per n generico:
i tratti totali sono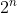 ;
; 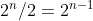 orizzontali,
orizzontali, 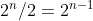 verticali
verticali
quindi un tratto orizzontale è lungo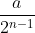
mentre un tratto verticale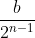
L(n)=L0rr(n)+ Lvert(n)
Lorr(n)=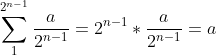
Lvert(n)=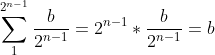
L(n)=L0rr(n)+ Lvert(n)=a+b quindi non dipende da n
Calcoliamo la lunghezza della curva,intesa come limite di curve ricorsive, facendo il limite per n-->infinito:
Questi calcoli potevano essere evitati, ma li ho fatti apposta per far vedere che per quanto si ripeta la ricorsione la lunghezza della curva non cambia.
La curva ricorsiva non è una retta
Dobbiamo adesso astrarci completamente dalla nostra idea di curva o funzione. Il risultato a cui perverremo potrà sembrare assurdo, ma teniamo conto del fatto che la nostra curva non è definita in un modo tradizionale.
Pensando ad un numero sempre più grande di ricorsioni, ci immaginiamo visivamente che prima o poi vedremo una retta. Ma questa è solo una nostra intuizione. In realtà se poi prendiamo un punto e lo ingrandiamo, avremo delle sorprese. Pensate a delle coste viste da un areo; possono sembrare con dei contorni continui, ma più ci avviciniamo più diventano frastagliate, e addirittura assomigliano all'intera costa stessa. Un altro esempio: disegnate un segmento con un programma di immagini; ingrandite il segmento e prima o poi troverete una gradinata formata dai pixel. Aumentate la risoluzione dell' immagine e ridisegnate la retta; dovrete fare degli ingrandimenti più grandi ma ritroverete sempre la gradinata di pixel. Per noi la risoluzione sarà legata al numero di ricorsioni, mentre gli ingrandimenti saranno dei cambiamenti di scala.
In matematica ingrandire significa eseguire dei cambiamenti di scala.
Prendiamo adesso un punto x0 e il corrispondente punto P su una retta. Se consideriamo fattori di scala sempre più grandi intorno al punto X0 troviamo sempre dei segmenti (contenuti nella retta). La curva , invece, vista su qualsiasi scala è identica a se stessa, a causa della ricorsione. In parole povere:se facciamo un ingrandimento in un intorno di un punto su una retta, otteniamo sempre un segmento di retta. Ma se lo facciamo sulla nostra curva che apparentemente sembra una retta, ritroviamo sempre qualcosa di simile alla gradinata.
Quindi nessun paradosso; anche se apparentemente sembra tendere ad una retta vista su una certa scala, in realtà resta sempre una gradinata, e quindi ritorniamo al fatto che la sua la sua lunghezza è data da a+b; non possiamo usare il teorema di Pitagora applicato ai cateti a e b. Notiamo inoltre che per nessun valore di n i gradini degenerano a un punto; la loro grandezza orizzontale è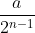 ,quella verticale
,quella verticale 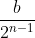 ; questi sono numeri >0, è solo il loro estremo inferiore che è zero.
; questi sono numeri >0, è solo il loro estremo inferiore che è zero.
Ho scritto tempo fa un articolo su una curva ricorsiva qui, che però non è rettificabile come questa,la curva di Peano -Hilbert. Magari leggerlo può servire a qualcosa. Non penso di aver convinto tutti, ma mi riprometto di scrivere un articolo approfondito su una curva simile a questa.
aggiungo questo; un gradino non può diventare improvvisamente un segmento diagonale nemmeno con un passaggio al limite
Vorrei esprimere un dubbio di fondo su questo quiz.
L'ipotesi è che se definiamo la funzione "scala" , come la successione di funzioni "gradino" e riduciamo a valori infinitesimi le dimensioni dei gradini, aumentandone al contempo il numero, si giunge ad una sovrapposizione con la linea rappresentata dalla funzione "rampa", ossia la retta che congiunge gli estremi della scala. In questo modo la distanza calcolata diventerebbe la distanza pitagorica.
Si sta cercando di formalizzare questa visione.
Mi sembra però che questo equivalga a dire : prendiamo la funzione sinusoidale, essa si sviluppa come una serie di onde lungo l'asse x. Rimpicciolendo le dimensioni di queste onde (e quindi aumentandone il numero nell'intervallo studiato) ci avviciniamo sempre più all'asse x.
Al limite, quando l'ampiezza dell' onda è un infinitesimo, la lunghezza curvilinea, che misuro seguendo il profilo della sinusoide, si riduce alla lunghezza della sua proiezione sull'asse x.
Ma questo è vero? In questo caso la funzione è nota, è semplicemente "A*sen x", dove A è l'ampiezza della sinusoide.
Leggo ora il commento di Umberto con cui mi trovo pienamente d'accordo. La scala resta scala anche se non vedo i gradini, perché tale è la sua definizione. Un triangolo non diventa un punto solo perché lo guardo da lontano.
Io pensavo a un qualcosa del genere.... n trattini di lunghezza x
facendo tendere N a infinito (all'interno di un intervallo s) e quindi (?) x a xM si dovrebbero ottenere infiniti punti lungo la diagonale. Stessa cosa si potrebbe fare separatamente per y
Ha un qualche senso?
aggiungo una considerazione che so che non vi piace, ma...
quando faccio l'integrale di una funzione composta da infiniti punti (f(x)), la scompongo in tanti trattini orizzontali che mi determinano le aree da sommare. Se il numero delle aree tende a infinito, i trattini tendono alla curva f(x)...
Resto fermamente convinto che le misure 7 e 5 appartengano a due mondi non comunicanti. Nascono da due modi diversi di eseguire la misura e non c'è modo di confluire dall'uno all'altro, per quanto ci si spinga a scale infinitesime.
Un ultimo esempio che vorrei fare per sostenere la mia visione è questo...
Sull'asse x traccio una serie di cicloidi, usando un cerchio generatore di raggio R.
Se considero un certo numero N di queste cicloidi tra un punto A e un punto B dell'asse x posso dire con certezza che la misura della lunghezza degli N archi vale: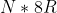 mentre la misura del segmento AB vale con certezza
mentre la misura del segmento AB vale con certezza 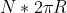
Il rapporto tra queste due misure vale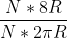
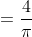
Questo rapporto è una sorta di fattore di forma che è invariante per qualsiasi scala di misura si possa scegliere.
Anche facendo rimpicciolire all'inverosimile R non cambia nulla perché R non è presente in quel rapporto.
In altri termini la somma della lunghezza degli archi è sempre superiore ( e sempre nella stessa proporzione) alla somma delle lunghezze delle loro ombre sul suolo orizzontale.
Esattamente come succede per la scala.
e negli integrali? la funzione da integrare passa da trattini a funzione continua quando il numero dei trattini tende a infinito.So che in realtà è l'area che fa tutto ciò, ma l'area è delimitata superiormente proprio da una funzione che nasce a scalini...e questa non resta a scalini, ma diventa una linea composta da infiniti punti...
Pensiamo pure a quegli infiniti punti e stabiliamo la regola di misura della distanza tra uno e l'altro.
In realtà posso definire quante regole riesco ad immaginare, eccone alcune.
Insomma si può andare avanti finché si vuole e tutte le misure hanno un loro significato: i punti sono sempre quelli ma i saltini che faccio da uno all'altro hanno forme diverse e portano a numeri diversi. L'unica cosa che accomuna queste misure tra loro è proprio il numero di saltini, che dipende da quanto ho segmentato la variabile, ossia fino a che punto ho rimpicciolito gli intervalli. Anche se i saltini sono infiniti le "misure" restano comunque fedeli allo "stampino" che ho scelto e quindi diverse tra loro. (Tutte valide)
caro Mau,
direi che mi sono abbastanza convinto. Per due punti passano infinite funzioni e la misura della loro distanza dipende dalla curva che ho stabilito. Se voglio la minima distanza, in campo puramente geometrico, questa curva è la retta (a cui si applica Pitagora). Se introducessi il moto, e quindi il tempo, diventerebbe la cicloide... se introducessi un animaletto troppo piccolo per saltare diventerebbe una funzione a gradini che degenererebbe nella retta quando gli scalini sono alla portata della formica.
Che ne dite?
Scrivo ancora due cose e poi basta.
Nel caso dell'integrale la questione è diversa; abbiamo una curva assegnata e costruiamo sotto (o sopra)il rettangoloide. Un punto dei trattini appartiene sempre alla retta; in ogni caso qui stiamo cercando l'area sottesa il cui limite è l'area del trapezoide. In ogni caso, per me, non è il rettangoloide che tende alla curva, ma la sua area. Per dirla ancora meglio è l'estremo superiore delle somme delle aree dei rettangoloidi inscritti
nel nostro caso non costruisco la scalinata basandomi sulla retta, ma sui due punti. Smangiucchiando dei gradini posso finire sotto la retta, e normalmente dei gradini ci stanno sopra. Qui cerchiamo invece la curva che si ottiene unendo A e B con infiniti gradini
comunque per me il discorso resta semplice, e mi limito alla domanda del quiz:
La lunghezza della scalinata è a+b
Invece di complicarci la vita con le funzioni ricorsive, consideriamo una scalinata qualsiasi e siano ai, bi la base e l'altezza dello scalino. L''unico vincolo imposto è che gli scalini siano ortogonali. se proiettiamo le parti verticali e quelle orizzontali rispettivamente su a e b, non facciamo altro che suddividere a e b, ma se poi sommiamo queste suddivisioni otteniamo ancora a e b. Questo qualsiasi sia la gradinata, finita o infinita; sono quantità costanti, non dipendono dalle suddivisioni. Quindi la lunghezza è sempre a+b. Non so chi potrebbe dimostrare che non è valido questo ragionamento. La curva non può essere un retta, perchè altrimenti la sua lunghezza sarebbe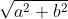 ; ma così non è. Quindi la curva non è una retta,ma una scala con infiniti gradini.
; ma così non è. Quindi la curva non è una retta,ma una scala con infiniti gradini.
e potremmo tagliare la testa al toro... dici bene!
Io ho implementato il ragionamento su geogebra. Andando a vedere qui:
https://ggbm.at/jtqSRDSt
si nota che, aumentando il numero di gradini (con l'apposito cursore in alto a sinistra, da 2 a 10 gradini), questi restano sempre sopra l'ipotenusa del triangolo OAB. Per quanto numerosi siano, la somma dei due cateti di tutti i triangolini sopra l'ipotenusa di OAB sarà sempre maggiore di AB, esattamente resta costante e pari proprio ad (a+b). Potrei aumentare quanto voglio il numero dei gradini, ma potrò sempre fare uno zoom (scalare, come dice Umberto) e constatare sempre che la somma dei cateti non arriva mai ad essere pari all'ipotenusa. Sono e restano due cose diverse.
Ovviamente, Artù, anche se gli scalini stanno un po' sopra e un po' sotto.... come nella figura che avevo fatto qualche commento fa...
Certo, Prof, la posizione dell'ipotenusa rispetto ai gradini, se sotto, sopra o in mezzo, è ininfluente ai fini della differenza tra lunghezza dell'ipotenusa e lunghezza della somma dei cateti dei triangolini. Se partendo da 2 gradini, li aumento a 4, posso sempre ingrandire (scalare) del doppio e mi ritrovo, in quanto a differenza tra ipotenusa e cateti dei triangolini, alla situazione di partenza. Più aumento il numero dei gradini, più posso ingrandire, se li aumento a 100 , ingrandisco di 100 volte e mi ritrovo sempre con una scala, diversa da uno scivolo (ipotenusa). In definitiva, non c'è paradosso. Siamo portati a pensare che facendo tendere ad infinito il numero dei gradini, la scala alla fine diventi geometricamente uno scivolo , ma in realtà resta sempre una scala di lunghezza (lungo alzate e pedate) pari ad (a+b).
L'unica via, per la formica, di abbreviare realmente il percorso è salire lungo il battiscopa (se anche questo non è seghettato)
Mi ha riferito proprio ora il fido Arlei che ne ha parlato con delle sue amiche formiche e gli hanno confermato che la cosa funziona come dicono Artù e Umberto. Hanno anche detto che, per comodità loro aspettano che passi qualcuno, salgono sulle scarpe e poi scendono alla fine della scala, tipo autobus.
A me ricorda una nube di diffusione di valori attorno alla loro media: leggasi deviazione standard,
calcolata sugli scarti quadratici medi delle distanze dei vertici di angolo 90° degli scalini dall'ipotenusa del triangolo madre.
Sino a quando ci sono scalini (ovvero la distanza dei singoli vertici dei triangolini dall'ipotenusa è > 0) la deviazione standard è positiva, quando il limite per il numero di scalini tende all'infinito, la deviazione standard si annulla.
La deviazione standard ci indica che la somma delle misure (7) tende al suo valore medio (5).
Mi turba la tua frase Andy... gli altri che ne dicono?
Non andrei sulla statistica e il calcolo delle probabilità.. in fin dei conti qui le divisioni dei gradini possono essere ben determinate, come per esempio dalla ricorsione. Comunque questo quiz che all'inizio avevo preso un po' alla leggera si è rilevato uno dei più interessanti visti ultimamente nel blog, in quanto tocca da molto da vicino le fondamenta delle rettificazioni delle curve e quindi del calcolo differenziale-integrale. Argomenti alla base della matematica "moderna" ma mai approfonditi in quanto mascherati dal calcolo differenziale-integrale,dove con i dx,dy e ds si risolve sempre tutto. Consiste essenzialmente nella differenza fra Newton e Leibniz.
mamma mia che grande onore per il circolo!!!!!
Deviazione standard e scarto quadratico medio sono strumenti statistici che si usano per misurare la variabilità di un determinato carattere in una popolazione.
Sei sicuro, Andy, che abbia senso usarli in questo contesto?
Ops... leggo solo ora il commento di Umberto che, in pratica, risponde alla mia domanda.
Cara Daniela,
no, non ne sono sicuro, la mia era una ipotesi, considerabile tra l'altro, solo se esiste una sola "rampa" di scalini (o sopra o sotto l'ipotenusa del triangolo principale), perché se gli scalini si trovano sopra e sotto, le singole distanze sono uguali e la loro differenza è sempre zero portando la deviazione standard ad essere costantemente nulla.
Che io ricordi, la deviazione standard è un indice che si applica non solo ad un determinato carattere della popolazione, ma in generale misura globalmente di quanto si discostano una serie di valori misurati, dalla loro media aritmetica (ad esempio una deviazione standard degli errori di misurazione di un determinato fenomeno).
Certo, ma, a mio parere, si tratta sempre di una misurazione statistica, di natura profondamente diversa da quella del problema posto nel quiz.
Almeno credo...
L'annullamento della deviazione standard indica che i punti che rappresentano l'insieme delle "letture" di una variabile (ad esempio un temperatura, una corrente elettrica , l'altezza degli individui in un gruppo, etc) appartengono alla curva di interpolazione, ma non fornisce informazioni sulla distanza tra punto e punto o sulla distanza tra gli estremi di un intervallo della interpolatrice che racchiude un certo numero di punti . Come già detto, la natura di questa distanza è arbitrariamente stabilita nel momento in cui scegliamo la "forma" del misuratore. Il valore della distanza resta legato a questa scelta.
Basta anche per me... mi sono convinto di essermi convinto di ciò che mi ero convinto di essermi convinto. Siete convinti anche voi????? CONOSCENZA COLLETTIVA
Io non ci ho capito un piffero, ma se tu, Enzone-steso-a-pelle-di-leone, sei convinto di essere convinto, allora mi fido!
Comunque, caro Oreste, su Papalla le formiche a volte rotolano sugli scalini senza scivolare e altre volte scivolano senza rotolare... per non farle stancare troppo, non sarebbe meglio sostituire gli scalini con una cicloide tautocrona e anche un pochino brachi-quacchecosa?!?
Se non mi sai rispondere tu, possiamo sempre chiedere ad Arturo un'animazione con papalGeogebra!!
Cara Dany, le cicloidi dicono tutte di essere brachistocrone e tautocrone perché così, avendo due patologie, prendono il sussidio. Non c'è da fidarsi, meglio controllare bene
Prima di assumerle.... una bella TAC e l'esame del sangue, poi si decide se sono idonee o meno...
Noto con piacere, caro Mau, che anche tu sei steso a pelle di leone come Enzone, se mi scambi per Dany...!!!
Beh, non negherai che c'è una certa rassomiglianza...(intendo nello stile di scrittura impeccabile che vi caratterizza)
Per forza, gliel'ho insegnato io l'italiano a quel testone pelato lì!!
Una idea per arrivare alle radici del paradosso...
La domanda implicita è questa: riducendo la dimensione degli scalini si può ottenere il risultato di far coincidere ciascun punto della scala con un punto sulla linea retta? Questo equivale a dire che siamo riusciti a "spianare" i gradini, appiattendoli sul percorso euclideo e quindi la distanza si riduce da 5 a 7.
Nella figura qui sopra vediamo che dimezzando la misura dei gradini (si passa dalla linea blu a quella viola) raddoppia il numero di punti della scala che sono stati sospinti lungo la linea retta, ma la forma della scala non cambia, gli angoli della linea a zig zag sono sempre angoli retti. la somma dei versanti in salita e in discesa porta sempre allo stesso risultato. La distanza totale sarà sempre 7 anche se i punti sospinti sulla linea retta saranno il doppio, e poi il doppio del doppio e poi ....eccetera. La misura è una conseguenza della metodologia stabilita, e una questione di "forma dei gradini"
Vediamo un modo alternativo di ricondurre la scala alla retta, occorre un topo più estroso, che rosicchia con una strategia diversa, non pretende di raddoppiare ogni volta i punti sulla retta, ma si accontenta solo di avvicinare ad essa tutti i punti, rosicchiata dopo rosicchiata, tutti insieme, sempre più vicini all'obiettivo.
Ecco cosa succederebbe...
Il topo rosicchia tutto quello che trova tra la linea blu e la linea verde. Cambia la pendenza dei gradini, non il loro numero.
Ogni volta la pendenza diminuisce e, alla fine, si arriva a "pendenza zero". Adesso sì che la scala è davvero appiattita. Tutti i suoi punti sono contenuti sulla retta. E la misura ? cosa succede alla misura?
Bene, la misura è la somma dei lati dei gradini. nella figura guardiamo il triangolo formato dai lati a b p.
i lati inclinati a e b sono il percorso della misura lungo la scala (inizialmente formano un angolo retto) il lato p è il percorso della misura euclidea.
le due misure sono legate da questa relazione^2})
ma cosa è h ? Semplicemente l'altezza di quel triangolo, la massima distanza che può avere un punto della scala dalla retta, E' il punto di discontinuità tra alzata e pedata del gradino.
E cosa succede ad ogni rosicchiamento? si riduce questa distanza h e, proporzionalmente, anche quella di tutti gli altri punti. insomma si passa da una linea blu alla verde , meno inclinata. L'angolo non è più retto ma diventa sempre più ottuso.
Quando raggiungiamo il limite , per h=0 quella distanza a+b diventa = p non è più 7 ma è diventata 5 in modo progressivo.L'ingegnoso topo è riuscito a portare tutti i punti della scala sulla retta con una strategia diversa da quella del suo collega che raddoppia ad ogni passaggio i punti trasferiti sulla retta ma non cambia la forma della scala.
Il criterio di misura della distanza lungo la scala , per il nostro topo eclettico, cambia ogni volta, Parte con "la distanza del taxista" poi già al primo passaggio adotta un ibrido tra "distanza del taxista" e "distanza euclidea" e lo spinge sempre più verso il modello "distanza euclidea". Le due distanze "del taxista" e "di Eucide" sono solo casi particolari, poli estremi, della ben più generale "distanza del Sorcio".
L'altro topo invece non cambia mai la sua scelta, usa sempre e solo la "distanza del taxista" non otterrà mai il risultato di una misura diversa. Purtroppo per lui la sua costanza non sarà premiata.
forse hai invertito 5 con 7 ...
Sì, grazie... ora ho corretto il commento mettendo il 5 e il 7 ai giusti posti.
sai non vorrei che adesso le scale andassero al contrario... mamma mia, speriamo che funzionino sempre gli ascensori!
Tra parentesi... il tuo esempio è simile a quello della scala mobile?????
Sai che non è mica male questa tua osservazione? in effetti si passa da una misura euclidea , all'inizio con i primi gradini appiattiti, a una misura del taxi a metà scala, quando i gradini sono tutti "fuori" , e di nuovo alla misura euclidea, quando termina la salita e i gradini si appiattiscono. Però non c'è trippa per topi.
per topi no... ma per Pitagora può darsi...