La scala del Diavolo

Categorie: Matematica Teoria degli insiemi Tags: matematiche superiori Scritto da: Umberto Cibien Commenti:0

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

La scala del diavolo, ovvero la funzione di Cantor- Vitali.

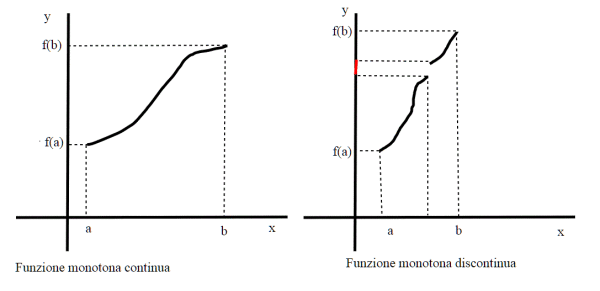
La scala del diavolo è una di quelle curve (come la curva di Peano e quella di Koch) che Hilbert definì "curve mostruose". Mentre la curva di Peano è una curva che riempe tutti i punti di un quadrato, e quella di Koch una funzione non derivabile in nessun punto, quella di Cantor-Vitali merita davvero il nome di "curva del diavolo". E' l'esempio di una curva debolmente crescente che ha derivata nulla in quasi tutti punti (chiariremo il significato di quel "quasi " più avanti). La curva cresce dal valore 0 al valore 1 senza però essere mai strettamente crescente. Nonostante questo non ha "salti" essendo una funzione continua. Inoltre mappa un insieme di misura nulla in un intervallo!

Cercherò di introdurre questo argomento non proprio facile nel modo più intuitivo possibile. Ci proponiamo di costruire una funzione sulla base di un insieme che abbiamo già conosciuto in questo articolo, l'insieme di Cantor. Penso che sia necessario riprendere le parti principali dell'articolo.

L'insieme di Cantor,costruzione.

Consideriamo il segmento chiuso AB=[0,1]. Dividiamo il segmento AB in tre parti uguali

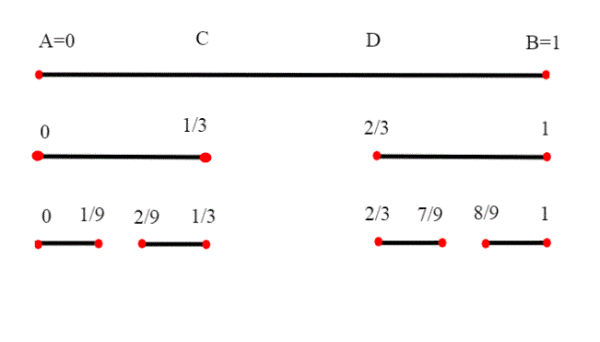
e togliamo dalla parte centrale il segmento aperto (C,D) otteniamo due segmenti chiusi, di lunghezza 1/3 di AB. Se ripetiamo il procedimento ai due segmenti rimasti, dividendoli sempre in tre parti otteniamo in tutto quattro segmenti, di lunghezza 1/9 di AB. Vogliamo estendere questo procedimento indefinitamente; cosa resta del segmento AB=[0,1] iniziale, dopo tutte le cancellazioni? L'insieme di Cantor. Osserviamo che non resta alcun segmento non degenere, infatti la lunghezza all'n-esima iterazione è $\frac{1}{3^{n}}$ , che ha come estremo inferiore 0 ,o (se preferite) limite zero.

Restano allora solo dei punti (da qui il termine suggestivo "polvere di Cantor"). L'insieme senz'altro non è vuoto(gli estremi di un segmento non vengono mai cancellati,viene solo tolta la parte centrale).

Ogni volta che dividiamo i segmenti successivi in tre parti e togliamo il segmento (aperto) centrale, abbiamo due scelte; prendere quello di sinistra, oppure quello di destra. Gli intervalli che corrispondono ad un certo ramo sono tutti incapsulati; ovvero ogni precedente contiene i successivo;sono intervalli chiusi e la loro ampiezza tende a zero (è uguale a $\frac{1}{3^{n}}$ ); per quanto abbiamo visto su gli intervalli incapsulati, la loro intersezione è un unico punto). Quindi per ogni ramo abbiamo nell'insieme di Cantor almeno un punto.

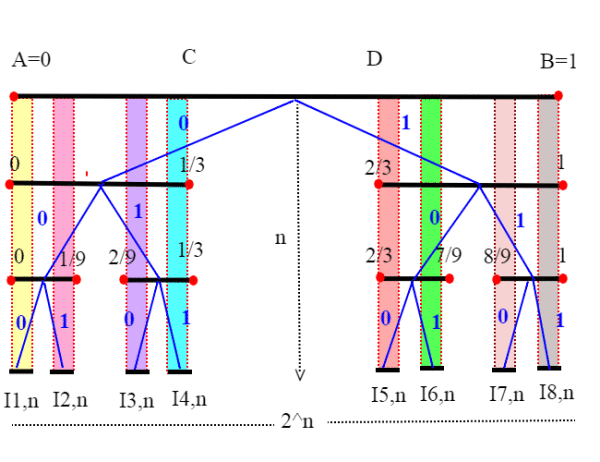
I rettangoli di vario colore evidenziano gli intervalli incapsulati; al passo n=3, abbiamo già $2^{3}=8$ successioni distinte di intervalli incapsulati. In generale , all' n-esimo passo ne abbiamo $2^{n}$ .

La cardinalità dell'insieme di Cantor

Nello stesso articolo e nel seguente abbiamo anche visto,sfruttando le successioni binarie infinite, che la cardinalità dell'insieme di Cantor è uguale a quella di R. Detto in parole povere: l'insieme di Cantor ha tanti punti quanti quelli della retta reale.

L'insieme di Cantor ha misura nulla.

Possiamo definire la misura di un intervallo, semplicemente facendo la differenza fra gli estremi.

Vogliamo vedere qual'è la misura totale delle cancellazioni che vengono eseguite partendo dall'intervallo [0,1]. Alla prima iterazione tolgo un segmento di lunghezza 1/3 ; alla seconda due segmenti di lunghezza 1/9, ovvero 2/9, alla terza 4 segmenti di lunghezza 1/27, ovvero 4/27 e così via. La somma S delle misure che tolgo è quindi S=1/3 + 2/9 + 4/27 + ... $2^{n-1}/3^{n}$ ..

Quindi S è somma della serie :

$S=\sum_{0}^{\infty}\frac{2^{n}}{3^{n+1}}=\frac{1}{3}\sum_{0}^{\infty}\frac{2^{n}}{3^{n}}$

abbiamo dunque un serie geometrica di ragione 2/3; sappiamo che la somma di tale serie è $\frac{1}{1-\frac{2}{3}}=3$ ,

S=3 *1/3

Quindi S=1.

Ma come definire la misura di un insieme di punti, come quello di Cantor? in questo caso possiamo farlo come differenza fra la misura di tutto l'intervallo e S. Ma allora la misura dell'insieme di Cantor è L(C)= L([0,1])-S=1-1=0

Costruzione grafico-intuitiva della funzione di Cantor-Vitali.

Vogliamo costruire una successione di funzioni che abbiano il valore 0 in 0 e il valore 1 in 1, cioè:

fn(0)=0, fn(1)=1

Tutte le fn devono essere debolmente crescenti.

Tutte le fn devono essere poi continue; le costruiremo con delle poligonali, che senz'altro sono delle funzioni continue.

Definiamo f0(x) il tratto obliquo che unisce [0,0] a [1,1], che quindi è una retta, di equazione y=x

Passiamo ora a f1.

Seguiamo sulle ascisse il metodo usato per generare l'insieme di Cantor;

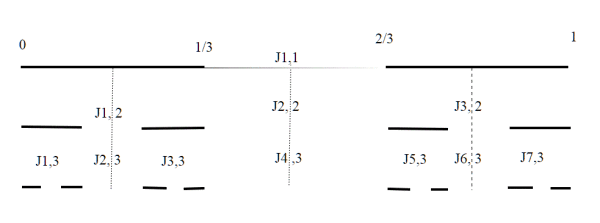
Dividiamo l'intervallo [0,1], che è il dominio della nostra funzione, inizialmente in tre parti uguali, come nella costruzione dell'insieme di Cantor. Nell'intervallo (1/3,2/3) che corrisponde ad uno degli intervalli tolti nel primo passo dell'insieme di Cantor, poniamo f1 costantemente uguale ad 1/2. Indichiamo con J1,1 il primo tratto tolto (n=1), mentre con I1,1,I2,1 gli intervalli che rimangono.

In pratica poniamo uguale a $\frac{k}{2^{n}}$ il valore della fn nell'intervallo jk,n. ( $\frac{1}{2^{1}}=\frac{1}{2}$ )

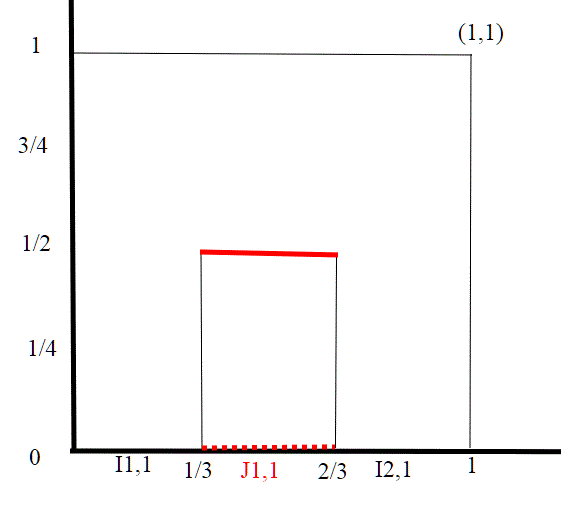
uniamo ora l'estremo sinistro del tratto orizzontale con (0,0), e l'stremo destro con (1,1)

le pendenze dei tratti obliqui sono ovviamente uguali e valgono 1/2/1/3=3/2. f1 risulta quindi definita su tutto [0,1]. Una osservazione importante; I1,1 è un intervallo chiuso, mentre J1,1 è un intervallo aperto, e in tutti i punti di questo intervallo f1 ha valore uguale ha quello che ha nel punto 1/3, che è un punto dell'insieme di Cantor.I tratti obliqui sottendono un intervallo chiuso sull'asse delle x in cui gli estremi (non venendo mai cancellati) sono punti dell'insieme di Cantor C.

passiamo a f2

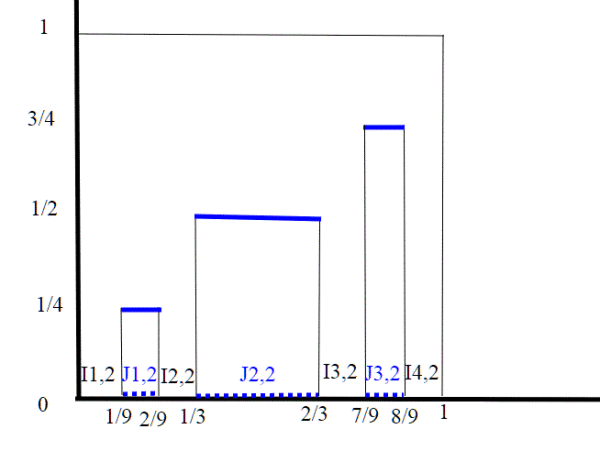
Continuiamo la nostra costruzione dell'insieme di Cantor sulle ascisse; gli intervalli tolti sono adesso 3 in totale, gli associamo secondo la regola di prima il valore $\frac{k}{2^{n}}$ ; in J1,2, $\frac{1}{2^{2}}=1/4$ , in j2,2 $\frac{2}{2^{2}}=1/2$ , in j3,2 $\frac{3}{2^{2}}=3/4$ .

Come per f1, cominciamo da (0,0) con il primo tratto obliquo, dopo di chè interpoliamo con dei tratti obliqui gli estremi destro-sinistro dei tratti orizzontali, fino ad arrivare in (1,1). Notiamo che la pendenza dei tratti obliqui(sempre costante) è aumentata, ed è uguale a 1/4/1/9= $(\frac{3}{3})^{2}$ . Chiaramente con questa costruzione possiamo andare avanti all'infinito. Abbiamo costruito una successione di funzioni. Non ci resta che definire funzione di Cantor, f(x), il limite di questa successione:

$f(x)=lim_{n \to +\infty}f_{n}(x)$ .

Che questa successione converga, è conseguenza di un criterio sulla convergenza uniforme di funzioni continue, ma questa volta dovete credermi sulla parola. Inoltre, essendo limite di una successione di funzioni continue, è anch'essa una funzione continua. Senza possedere queste importanti nozioni di convergenza, possiamo anche pensarla così: ad ogni iterazione affiniamo la nostra curva che diventa sempre più simile ad una gradinata. Se ingrandiamo un qualsiasi tratto della curva, ritroviamo sempre una poligonale che quindi è continua per costruzione.

In pratica seguendo passo passo il procedimento ricorsivo della costruzione dell'insieme di Cantor, costruiamo anche la scala del Diavolo. Nel disegno abbiamo messo in evidenza gli intervalli In,k , Jn,k. Gli I sono gli intervalli che restano ad ogni divisione, gli J quelli che vengono tolti. Notiamo che il valore costante che viene dato dentro gli J è proprio , se l'intervallo è Jn,k , fn(x)= $\frac{k}{2^{n}}$ . infatti, nell'intervallo J1,1 vale 1/2, in J1,2=1/4, in J3,2=3/4.

Quanti tratti orizzontali ha fn? quanti tratti verticali?

Sappiamo, per come la stiamo costruendo, che l'n-esima poligonale ha tanti tratti obliqui, quanti sono gli intervalli I della n-esima costruzione dell'insieme di Cantor, che sono $2^{n}$ , mentre i tratti orizzontali costanti sono tanti come gli intervalli J che togliamo ad ogni passo, cioè $2^{n}-1$ .

f0 ha infatti 1 tratto obliquo, $2^{0}=1$ , e nessun tratto orizzontale $2^{0}-1=0$

f1 2 obliqui, $2^{1}$ e 1 orizzontale, 2-1=1

f2 quattro obliqui $2^{2}$ , e tre orizzontali, $2^{2}-1=3$

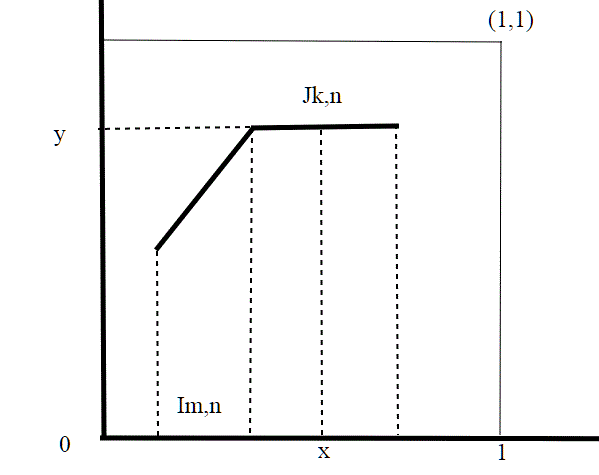
Perchè associamo in Jn,k ,ad f(x) il valore $\frac{k}{2^{n}}$ ? Riporto il disegno per capirci meglio.

Per una necessità di costruzione regolare, da tradurre analiticamente. Abbiamo appena visto che i tratti orizzontali sono $2^{n}-1$ . Ad essi dobbiamo associare un valore sulle ordinate; possiamo pensare di dividere in $2^{n}$ parti uguali l'intervallo [0,1]. Partendo da 0 e arrivando a 1 quanti punti ho generato? $2^{n}$ +1. Ma se tolgo 0 e 1 i punti interni diventano $2^{n}$ +1-2= $2^{n}-1$ . Quindi sono tanti come i tratti orizzontali. Inoltre negli Jk,n , k<= $2^{n}-1$ , quindi $\frac{k}{2^{n}}$ <1. L'importante poi è che tale valore, a parità di intervallo J, non dipenda da n, ovvero dal passo della costruzione. Con un po' di fatica e guardando il disegno sotto ci si rende conto che Jk,n-1=J2k,n, e quindi $\frac{k}{2^{n-1}}=2\cdot \frac{k}{2^{n}}$

Quant'è la pendenza del lato obliquo? $(\frac{3}{{2}})^{n}$ ;

Infatti l'intervallo proiettato sull'ordinata del tratto obliquo misura $1/2^{n}$ , il tratto orizzontale della proiezione $1/3^{n}$ , quindi il rapporto $(\frac{3}{{2}})^{n}$ .

se n=0,1,2 come nei disegni,la pendenza vale rispettivamente 1, 3/2, 9/4.

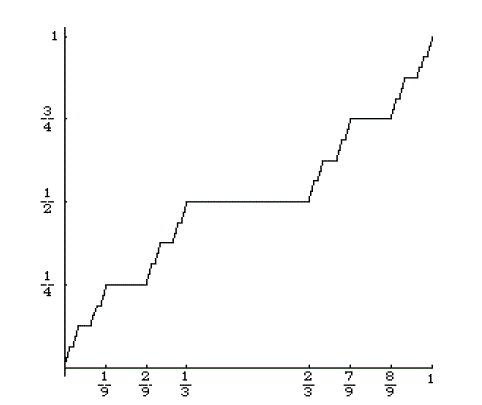
Notiamo che quando n diventa molto grande, la pendenza tende ad infinito, ovvero le spezzate tendono a dei gradini verticali, e sono sempre più corte. Da qui il nome di "scala" Il diavolo c’entra per vari motivi: uno è che pur avendo dei gradini, il grafico non ha nessun salto (la funzione è continua!) . Un altro modo in cui mette alla prova la nostra intuizione è che, pur crescendo dal valore 0 al valore 1, non è strettamente crescente su alcun sottointervallo non degenere di [0, 1]. Per giustificare questo fatto dobbiamo tener ben presente l’insieme di Cantor ricordandoci che su ogni sotto intervallo di [0,1 ] c’è sempre un segmento in cui la funzione risulta costante. Supponiamo per esempio di prendere un intervallo in cui la funzione cresce strettamente (lato obliquo), questo è un intervallo che poi andrà diviso in tre parti, e conterrà una parte costante.

Iniettività e suriettività

La funzione non è iniettiva; sappiamo infatti che negli intervalli che non appartengono all'insieme di Cantor, la funzione è costante, quindi per valori di x diversi, dà lo stesso f(x).

monotone — Il fatto che una funzione continua assuma tutti i valori fra f(a) e f(b) è giustificabile dal disegno; la f a destra non essendo continua perde i valori indicati in rosso.

E' però suriettiva, ovvero copre tutto [0,1]; essendo continua , debolmente crescente e inoltre f(0)=0, f(1)=1. Quindi assume tutti i valori fra 0 e 1.

Un fatto eccezionale:

L'immagine dell'insieme C di Cantor è tutto l'intervallo , ovvero f(C)=[0,1] !

Questo significa che l'immagine di un insieme di misura nulla ha come immagine un intervallo!

Vediamo se riusciamo a giustificarlo. Prendiamo un $y\in[0,1]$ ; essendo suriettiva,sappiamo che esiste un $x\in [0,1]$

tale che f(x)=y. Se $x\in C$ abbiamo finito. Se x non appartiene a C, allora appartiene ad uno degli intervalli che abbiamo tolto durante la costruzione, Jk,n. Ma f è costante su Jk,n, quindi nell'estremo sinistro assume lo stesso valore dell'estremo destro di un intervallo in cui la funzione è obliqua. Ma l'estremo come sappiamo dalla costruzione dell'insieme di Cantor, appartiene a C.

Il "quasi ovunque" della matematica.

Prima di continuare il discorso sulle strane proprietà della scala del diavolo, volevo introdurre i discorso del "quasi ovunque" in matematica. Esso deriva sostanzialmente dalla necessità di estendere delle proprietà che non sono sempre vere in un insieme prendendole sempre per buone lo stesso, a parte il fatto che esse non si verifichino solo su insieme di misura nulla. Riemann fu costretto a inventare una nuova definizione di integrale, affinché molte funzioni che fossero discontinue anche solo in un numero finito di punti, fossero lo stesso integrabili. Ebbene, dimostrò che seguendo la sua definizione, ogni funzione continua quasi ovunque è integrabile. Guarda caso, per costruire la scala del diavolo è stato preso un insieme infinito di misura nulla, l'insieme di Cantor, e che ha addirittura la stessa cardinalità del continuo.

La funzione di Cantor-Vitali è derivabile quasi ovunque.

Sappiamo infatti, che comunque prendiamo un segmento , dobbiamo tener ben presente l’insieme di Cantor ricordandoci che su ogni sotto intervallo di [0,1 ] c’è sempre un segmento in cui la funzione risulta costante Quindi al di fuori dell'insieme di Cantor, ovvero al di fuori di un insieme di misura nulla, la funzione è sempre derivabile, con derivata nulla.

Più in dettaglio:Jk,n non appartiene a C ed è un insieme aperto e in esso la derivata è nulla, mentre l'estremo destro di Im,n appartiene a C. Tale estremo infatti non viene mai tolto, ma nello spigolo la derivata non esiste. In quanti punti non è derivabile? Solo nei punti dell'insieme di Cantor.

Lunghezza della funzione di Cantor.

Nel quiz sul paradosso della scala e della formica, avevamo concluso che la lunghezza della scala era la somma dei cateti, a e b. Lì il discorso era però diverso; la scala partiva già con dei gradini verticali, e comunque si suddividessero ottenevamo come lunghezza sempre la somma delle proiezioni, che sono appunto a. b. Se pensiamo adesso alla lunghezza dei nostri tratti orizzontali, sulla scala, e li proiettiamo sull'asse delle x, altro non otteniamo che la lunghezza del complementare dell'insieme di Cantor, che abbiamo già calcolato nella prima parte dell'articolo, ottenendo:

$S=\sum_{0}^{\infty}\frac{2^{n}}{3^{n+1}}=\frac{1}{3}\sum_{0}^{\infty}\frac{2^{n}}{3^{n}}$ =1

Scheeffer (1884) ha mostrato che la lunghezza della scala del diavolo è 2; da ciò ne deriva che la parte "inclinata" ha lunghezza 1, come intuitivamente si pensa tendendo i lati obliqui alla verticale. Questo non ci può stupire più di tanto, in quanto la funzione di Cantor ,come abbiamo visto,trasforma un insieme di punti, C, nell'intervallo [0,1].

Termino con questa osservazione, dedicata unicamente a chi conosce l'integrale di Riemann.

L’integrale della derivata della scala diabolica (quando essa è derivabile) non è la scala diabolica.

Chiamiamo come di consueto C l'insieme di Cantor. Allora, indicando con f ' (x) la derivata della funzione di Cantor, abbiamo:

$f^{'}(x)=\left\{\begin{matrix} 0 & x\in [0,1]-C\\ nonesiste & x\in C \end{matrix}\right.$

definiamo adesso una funzione g(x):

$g(x)=\left\{\begin{matrix} 0 & x\in [0,1]-C\\ S & x\in C \end{matrix}\right.$

dove S è un qualsiasi valore, ma non illimitato.

La funzione g è integrabile (secondo Riemann) perchè vale quasi sempre zero, a parte in un insieme di misura nulla,C.

$h(x)=\int_{0}^{x}g(t)dt=0$

quindi :

$h(x)\neq f(x)$

$0=h(x)=\int_{0}^{x}g(t)dt=\int_{0}^{x}f^{'}(t)dt\neq f(x)$

quindi l'integrale della derivata della scala diabolica, non è la scala diabolica.

In pratica con la scala di Cantor svanisce il tentativo di estendere il teorema fondamentale del calcolo integrale.

L	M	M	G	V	S	D
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

Articoli correlati

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

Il Problema di Apollonio e le "sue" coniche. 4 ***

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*